某二級斜齒圓柱齒輪減速器NVH性能預測及優化

魏顯坤，楊興國，賴天華

(1.重慶工商職業學院， 重慶 401520; 2.重慶耐世特轉向系統有限公司, 重慶 401520)

當前，隨著對噪聲污染認識水平的提高，人們對機械設備的NVH(Noise Vibration Harshness)性能也空前的重視。在現代工業中，齒輪以其高的效率、穩定的傳動比以及緊湊的結構等在機械傳動中起著至關重要的作用。因此，減速器在產品設計階段預測NVH性能和優化具有重要的現實意義。

國內外學者就齒輪系統減振降噪已經開展了廣泛的研究工作。對于齒輪-轉子系統振動響應的研究，提出了基于齒輪副集中參數模型的齒輪剛度激勵、嚙合沖擊激勵模擬方法[1-2],對齒輪-轉子系統進行固有特性及動態響應的數值仿真分析[3]，齒形修型對傳動誤差及

動態響應的影響[4-7]。對于殼體的動態特性及輻射噪聲的研究,應用聲固耦合的方法對殼體進行聲輻射分析[8]，就各面板對聲場聲壓貢獻度分析[9]，應用能量統計方法對殼體進行振動噪聲預測[10]。

1 減速器的振動噪聲與傳播路徑

減速器的噪聲主要表現為敲擊噪聲和嘯叫噪聲。前者是由于齒輪副存在間隙和動力源輸入的激勵為扭轉振動激勵而產生的，然而本減速器是以三相異步電機為動力源，其輸出轉速非常平穩，所以本減速器的敲擊噪聲理論上沒有或很小。而后者主要是由于齒輪的傳動誤差引起的，其原因有兩方面：一是齒輪本身的精度等因素影響；另一方面是由齒輪嚙合錯位造成的，嚙合錯位是由軸、軸承的變形導致的。 減速器振動噪聲傳播可分為三部分:振動經齒輪、軸、軸承等傳到殼體，通過殼體外壁振動而輻射到箱外空氣中，形成第一次空氣聲；箱內噪聲激發殼體振動，通過殼體輻射到箱外空氣中，形成第二次空氣聲；箱內噪聲通過各種縫隙傳到箱外。實驗表明，減速器噪聲中約90%～95%是通過振動傳遞，最后由齒輪箱殼體振動而輻射到箱外的[11]。振動噪聲傳遞路徑如圖1所示。

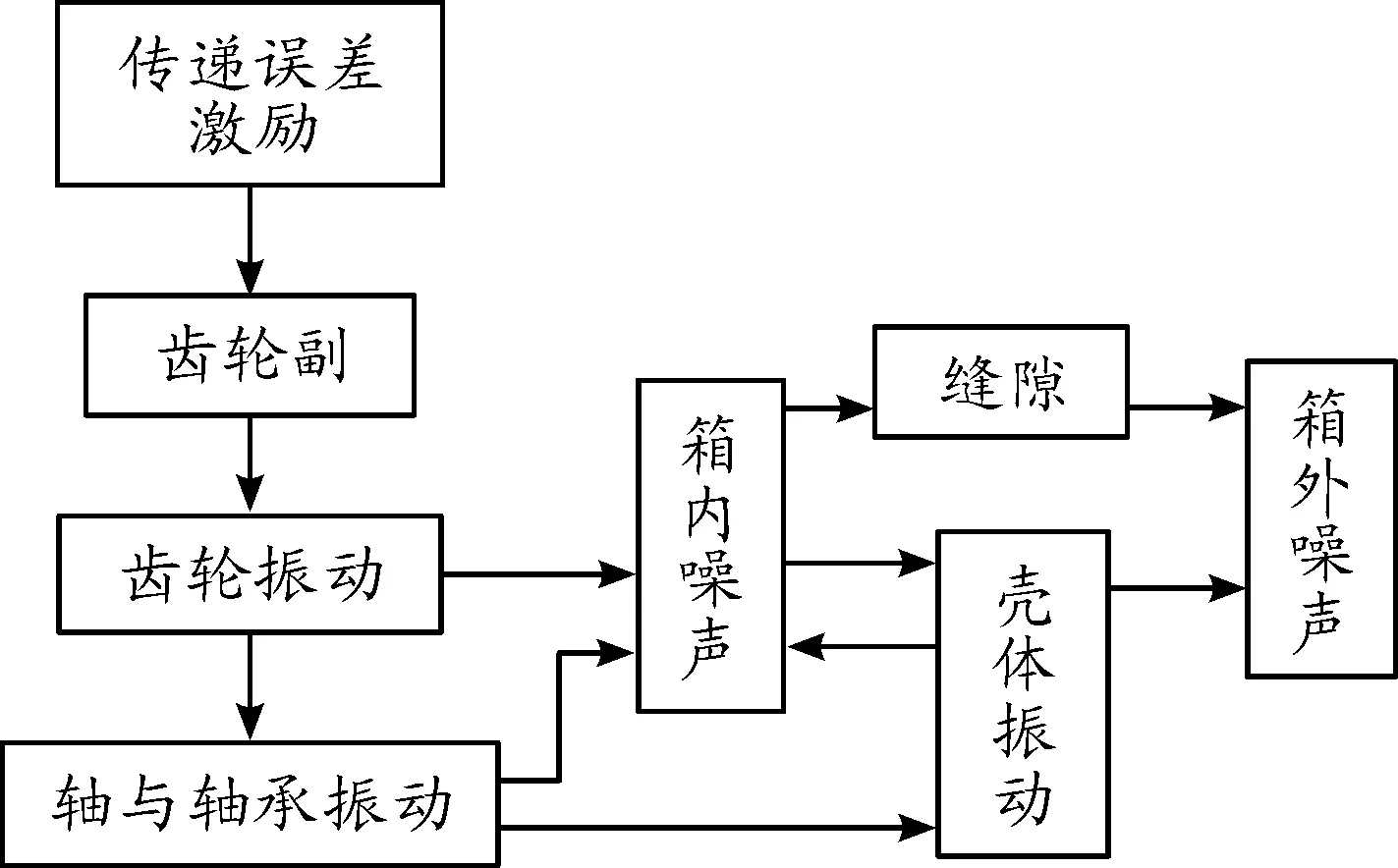
圖1 振動噪聲傳遞路徑

2 齒輪-轉子系統動態分析

2.1 齒輪-轉子系統Romax模型

在Romax軟件中，根據設計參數依次完成軸的建模、齒輪建模、軸承的選擇。齒輪建模分為概念建模和詳細建模，詳細建模包括定義齒輪的精度等級、表面粗糙度、變位系數和齒側間隙等。然后裝配成齒輪-轉子系統模型，如圖2所示。

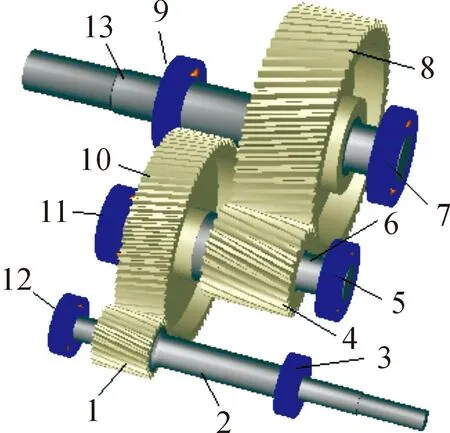
1.第一級主動齒輪; 2.輸入軸; 3.軸承2; 4.第二級主動齒輪; 5.軸承4; 6.中間軸; 7.軸承6; 8.第二級從動齒輪; 9.軸承5; 10.第一級從動齒輪; 11.軸承3; 12.軸承1; 13.輸出軸;

圖2 齒輪-轉子系統模型

2.2 傳動誤差激勵

傳動誤差是齒輪副實際嚙合點與理論嚙合點的偏差，可以表示為一對齒輪節圓相切點的線性偏差，所以定義傳動誤差為

TE=θc*rc-θz*rz

(1)

式中：θc為從動齒輪轉角；θz為主動齒輪轉角；rc為從動齒輪基圓半徑；rz主動齒輪基圓半徑。

在Romax軟件中進行齒輪-轉子系統動態分析時，是以齒輪傳動誤差為激勵的，同時考慮嚙合綜合剛度和系統固有特性的影響。齒輪副嚙合時載荷計算公式

{p}={po}+[k′]{e}

(2)

式中：{p}為載荷陣列；{po}為靜態載荷陣列；[k′]為嚙合綜合剛度矩陣；{e}為傳動誤差激勵。

本研究在校核齒輪、軸承以及軸的疲勞壽命和靜態分析后，計算得到兩級齒輪副傳動誤差如圖3所示。

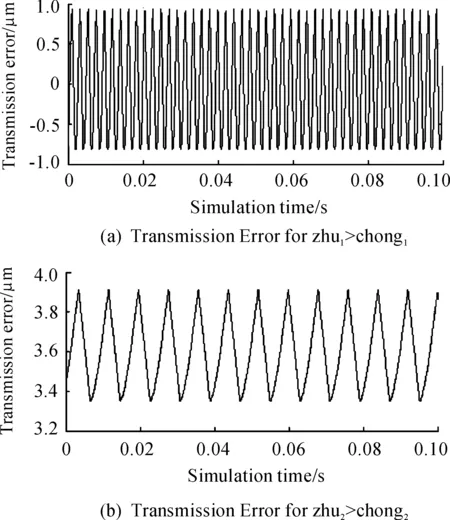
圖3 傳動誤差

第一級齒輪副傳動誤差值在-1～1 μm，其中最大值為0.94 μm，最小值為-0.82 μm，相差1.76 μm。第二級齒輪副傳動誤差值在3.3～4 μm，其中最大值為3.92 μm，最小值為3.37 μm，相差0.55 μm。產生傳遞誤差的原因有齒輪的精度誤差、表面粗糙度以及齒輪軸和軸承變形引起的嚙合錯位。

2.3 齒輪-轉子系統模態分析

應用Romax軟件中的NVH模塊，可以計算得到齒輪-轉子系統各階模態的固有頻率和振型，如表1所示。本減速器的齒輪-轉子系統的前25階模態的固有頻率范圍為182～4 209 Hz，若激勵頻率與齒輪-轉子系統的固有頻率重合容易引發共振，該頻率下的激勵將被放大后傳遞到殼體上。

2.4 齒輪-轉子系統振動響應

在兩級齒輪傳遞誤差的激勵下，齒輪-轉子系統發生振動，圖4分別是輸入軸和輸出軸安裝第一級主動齒輪和第二級從動齒輪處的響應加速度曲線。其中，振動加速度出現在頻率為3 366 Hz和2 330 Hz處，值為743 m/s2和69.6 m/s2，分別對應齒輪-轉子系統的第19階和第21階固有頻率。

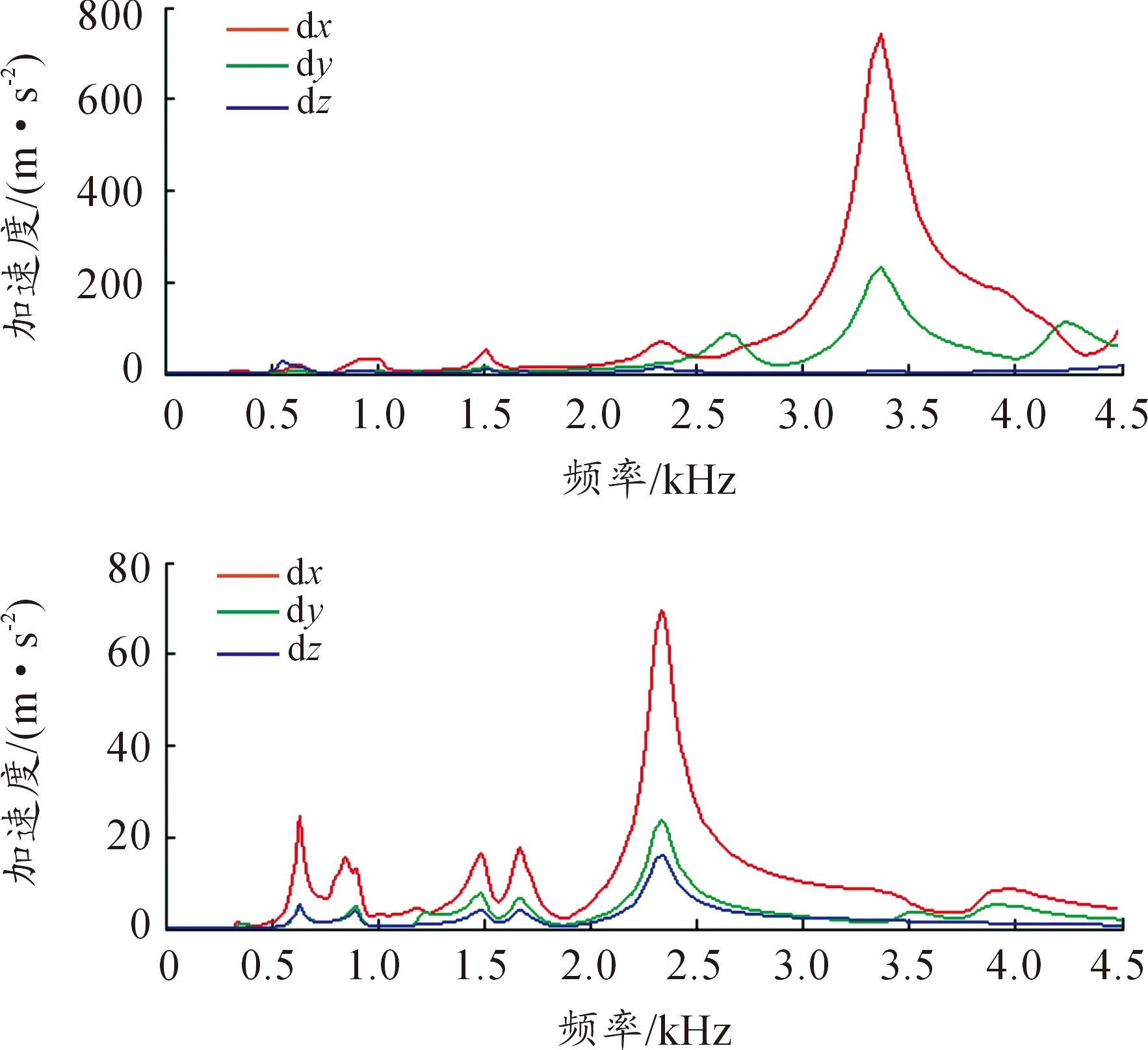
圖4 輸入/出軸振動加速度幅值譜

齒輪-轉子系統的振動會向周圍空間(箱內空間)輻射噪聲，由于輻射的表面積較小和殼體等密封件的隔聲作用，該噪聲傳遞到箱外很少，不給予考慮。本研究重點關注軸承傳遞給殼體的作用力，圖5是軸承1～6在X軸、Y軸和Z軸的作用力幅值譜。可以看出，各個峰值都出現在齒輪-轉子系統的固有頻率處，說明齒輪-轉子系統的固有特性對軸承作用力影響巨大。

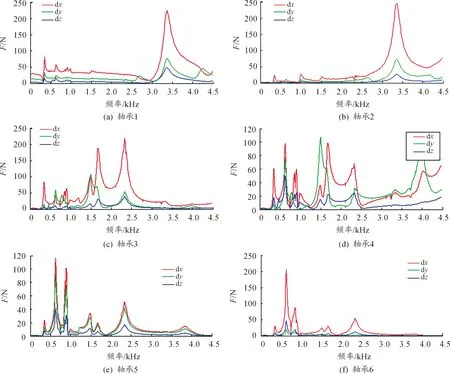
圖5 軸承作用力幅值譜

3 殼體的振動分析

3.1 模態分析

模態分析主要用于確定零件或部件的固有特性，即各階模態。殼體是減速器聲輻射的主要部件，其固有特性對整個減速器的NVH性能起著至關重要的作用。通過模態分析，可以得到殼體的固有頻率和振型，為減速器NVH性能預測和優化提供重要幫助和參考。模態振型如圖6所示。

對于多自由度線性定常系統，建立結構的動力學方程為

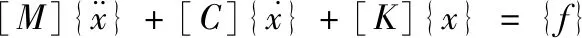
(3)

式中：[M]為總質量矩陣；[C]為總阻尼矩陣；[K]為總剛度矩陣；{f}為節點等效載荷列陣；{x}為節點位移列陣。

在結構的動力學方程中，令[C]=0和{f}=0，得到無阻尼自由振動方程為

(4)

式(4)的特征方程為

(5)

求解特征方程的前n個特征值，這n個特征值就是結構的前n階固有頻率。

本文將Creo Parametric建立的減速器殼體三維模型導入前處理軟件ANSA中建立有限元模型，然后應用ANSYS求解器進行計算并進行后處理。本文計算殼體在約束條件下且固有頻率在4 500 Hz內的模態，表2是殼體前20階固有頻率及振型描述。

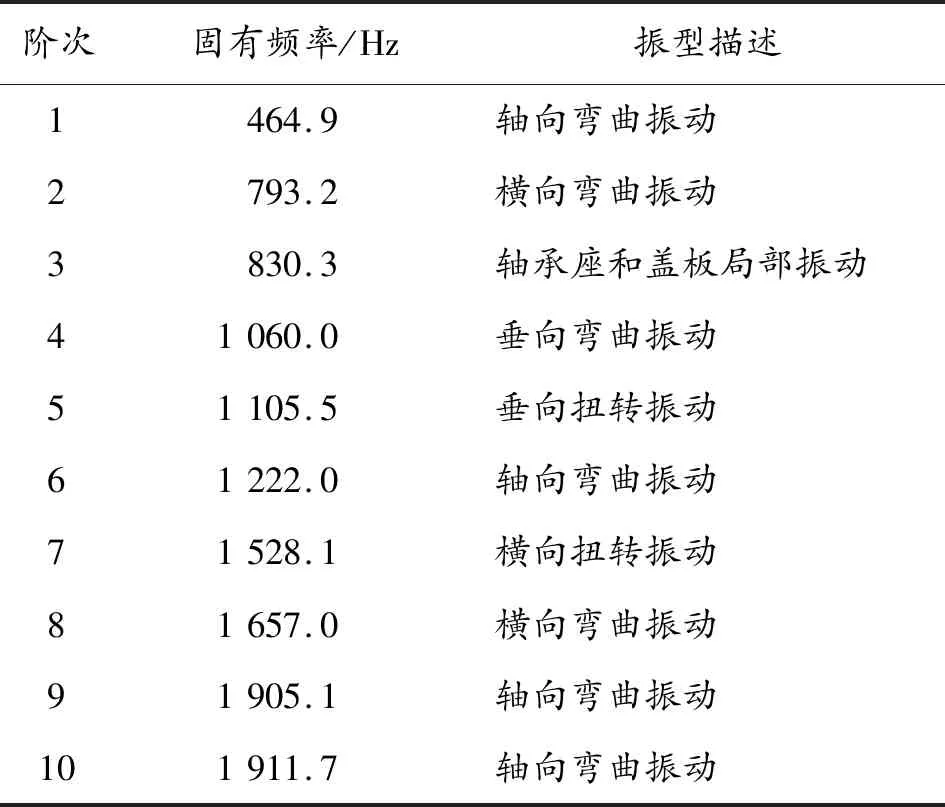
表2 殼體前20階約束模態

3.2 振動響應分析

減速器殼體是由大板件組成，在外在激勵下容易激發大的振動，聲輻射效率較高，是加速器聲輻射的主要部件，所以它的振動是決定減速器NVH性能的關鍵。如圖1所示，殼體振動由兩部分組成：一是箱內噪聲傳到殼體內壁上，激發殼體振動，同時殼體振動也向箱內輻射噪聲；二是振動經齒輪、軸和軸承傳遞到殼體上，激發殼體振動。因為減速器殼體剛度較大，聲音激起的振動非常小，所以殼體的振動主要是后者。

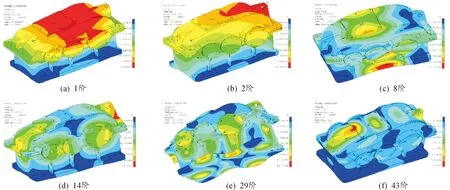
圖6 模態振型

本研究以2.4節的軸承作用力及其相位作為激勵，應用模態疊加法計算殼體的振動響應，得到的結果可以作為邊界元法計算殼體聲輻射的邊界條件。圖7是箱蓋后端某點的振動加速度頻譜和箱蓋前端某點的振動加速度頻譜，后點振動加速度在3 370 Hz時有最大值為101.7 m/s2，主要是軸承1和軸承2的激勵引起的，其他峰值頻率分別對應殼體的第1階、第2階、第4階、第8階、第9階、第14階及第39階固有頻率；前點振動加速度在3 320 Hz時有最大值為190.8 m/s2，主要是殼體的第29階模態和軸承作用力引起的，其他峰值頻率分別對應殼體的第1階、第2階、第4階、第8階、及第14階固有頻率。

圖7 振動加速度幅值譜

4 殼體聲輻射預測

4.1 ATV和MATV方法

在小壓力擾動情況下，可以認為聲學方程是線性的，因而可以將結構表面的振動和某場點聲壓之間建立某種線性對應關系，把結構表面離散成有限個單元，這樣在某場點的聲壓為

p={ATV(ω)}T{νn(ω)}

(6)

式中:ATV(ω)為聲傳遞矢量(Acoustic Transfer Vector)；νn為結構表面法向振動速度；ω為圓頻率。

通過聲傳遞矢量，可以在聲場中某場點聲壓與模型振動速度之間建立聯系，ATV的物理意義可以理解為節點或單元在某頻率下的單位模型振動速度在某場點上引起的聲壓值。

另外，結構振動位移響應可以通過模態線性疊加得到，即

{x}=Ω*{MRSP(ω)}

(7)

式中：{x}為結構位移；Ω為結構模態矩陣；MRSP(ω)為模態參與因子向量。

將結構表面振動的位移向量{x}投影到結構表面的法向上，就可以得到結構在法向的振動速度

{vn}=jωΩn{MRSP(ω)}

(8)

式中Ωn是結構振動模態在結構表面法向分矢量組成的矩陣，由此可以得到聲場中任意場點的聲壓為

p={ATV(ω)}T·jωΩn·{MRSP(ω)}=

{MATV(ω)}T·{MRSP(ω)}

(9)

式中{MATV(ω)}T為模態聲傳遞矢量(Model Acoustic Transfer Vector),{MATV(ω)}T的表達式為

{MATV(ω)}T=jωΩn·{MRSP(ω)}

(10)

MATV的物理意義為單元或節點在特定頻率下的單位模態響應在聲場中某場點處引起的聲壓值。

4.2 殼體的聲傳遞矢量

本研究在LMS Virtual.lab軟件中創建的邊界元模型，聲學網格采用線性網格，其最大尺寸小于最高計算頻率(4 500 Hz)點處的波長的六分之一；在殼體下方10 mm處創建對稱面，用來模擬地面；聲速為341 m/s,空氣密度為1.21 kg/m3,并生成ISO聲場，如圖8所示,該聲學邊界元模型共有19個場點組成。圖9是頻率為640 Hz、790 Hz、1 060 Hz、1 660 Hz、2 330 Hz以及3 300 Hz時聲學網格與19號場點的聲傳遞矢量云圖。可以看出在低頻時，底板表面的聲學傳遞矢量較大，而高頻時箱蓋表面的聲學傳遞矢量較大。

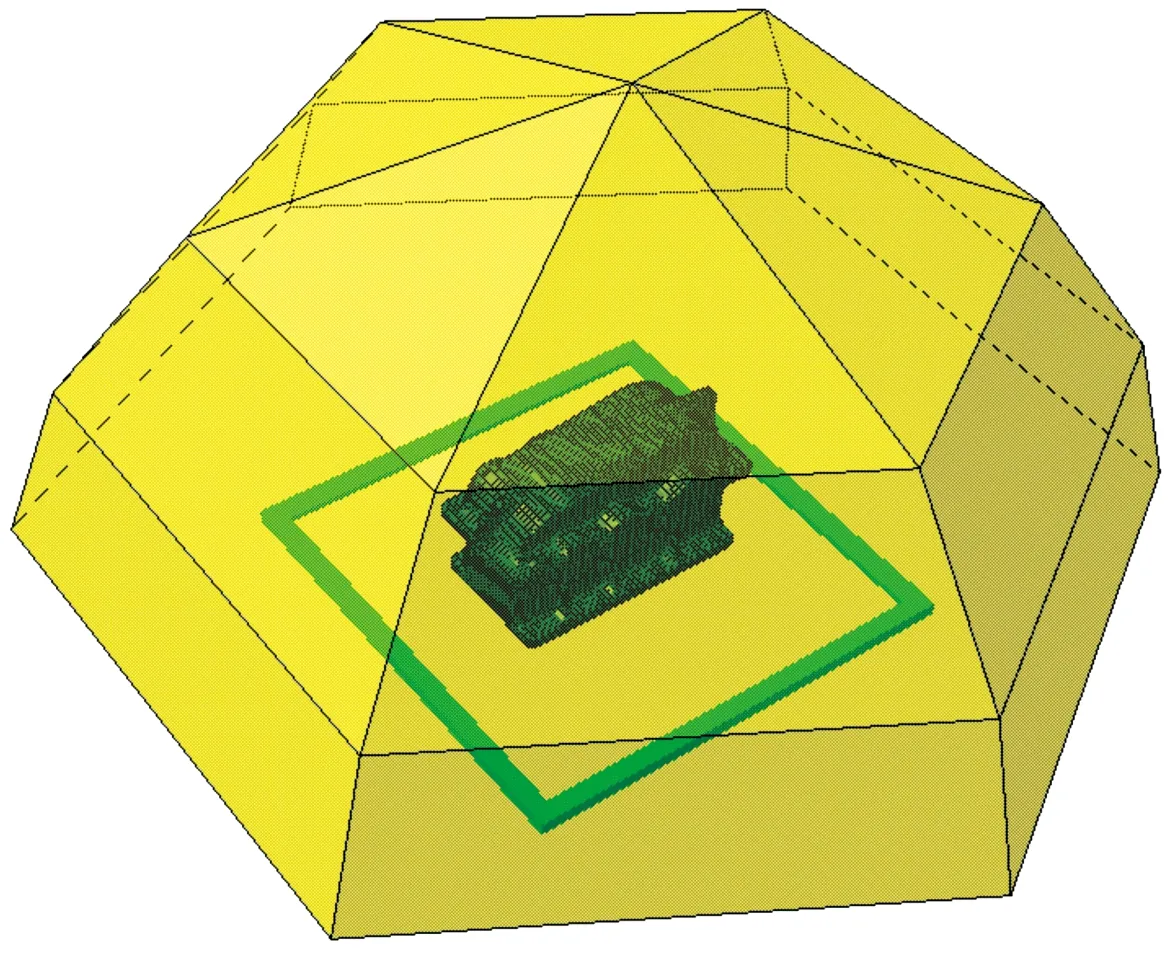
圖8 聲學邊界元模型

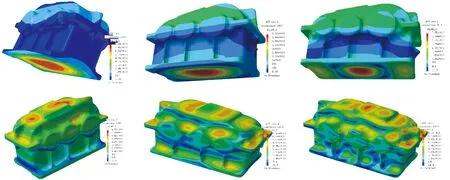
圖9 聲傳遞矢量云圖

4.3 殼體的聲輻射

聲功率是聲源在單位時間內輻射的聲能量，是描述聲源聲能量大小的量。在聲學中，聲功率用聲功率級表示

LW=10lg(W/W0)(dB)

(11)

式中：W0為基準聲功率；在空氣中取W0為10-12W。

圖10為殼體輻射的聲功率譜，峰值頻率(Hz)和聲功率級(dB)值分別為：(460,88.39)、(640,91.75)、(790,91.04)、(1 060,89.66)、(1 480,89.55)、(1 660,88.29)、(2 330,88.1)以及(3 300,92)。這些峰值都是殼體的強烈振動造成的，它們分別對應殼體的某階固有頻率或激勵的峰值頻率。其他頻率下的聲功率級集中在70～90 dB間，可以看出殼體輻射的聲能量較大，其原因是兩級齒輪嚙合狀態很差，造成大的傳動誤差造成的。

圖11為第19號場點聲壓譜，峰值頻率(Hz)和聲功率級(dB)值分別為：(460,86.26)、(640,19.75)、(910,80.38)、(1 060,90.85)、(2 030,85.13)、(2 290,85.16)以及(3 300,88.81)。圖12是第1～9號場點聲壓-頻率譜，圖13是第10～18號場點聲壓-頻率譜，圖14分別為頻率為460、640、790、1 060、1 480、1 660、2 330以及3 300時的聲場聲壓分布云圖。

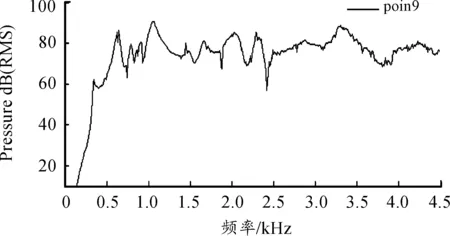
圖10 聲功率譜

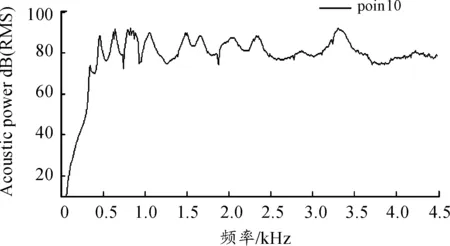
圖11 第19號場點聲壓譜

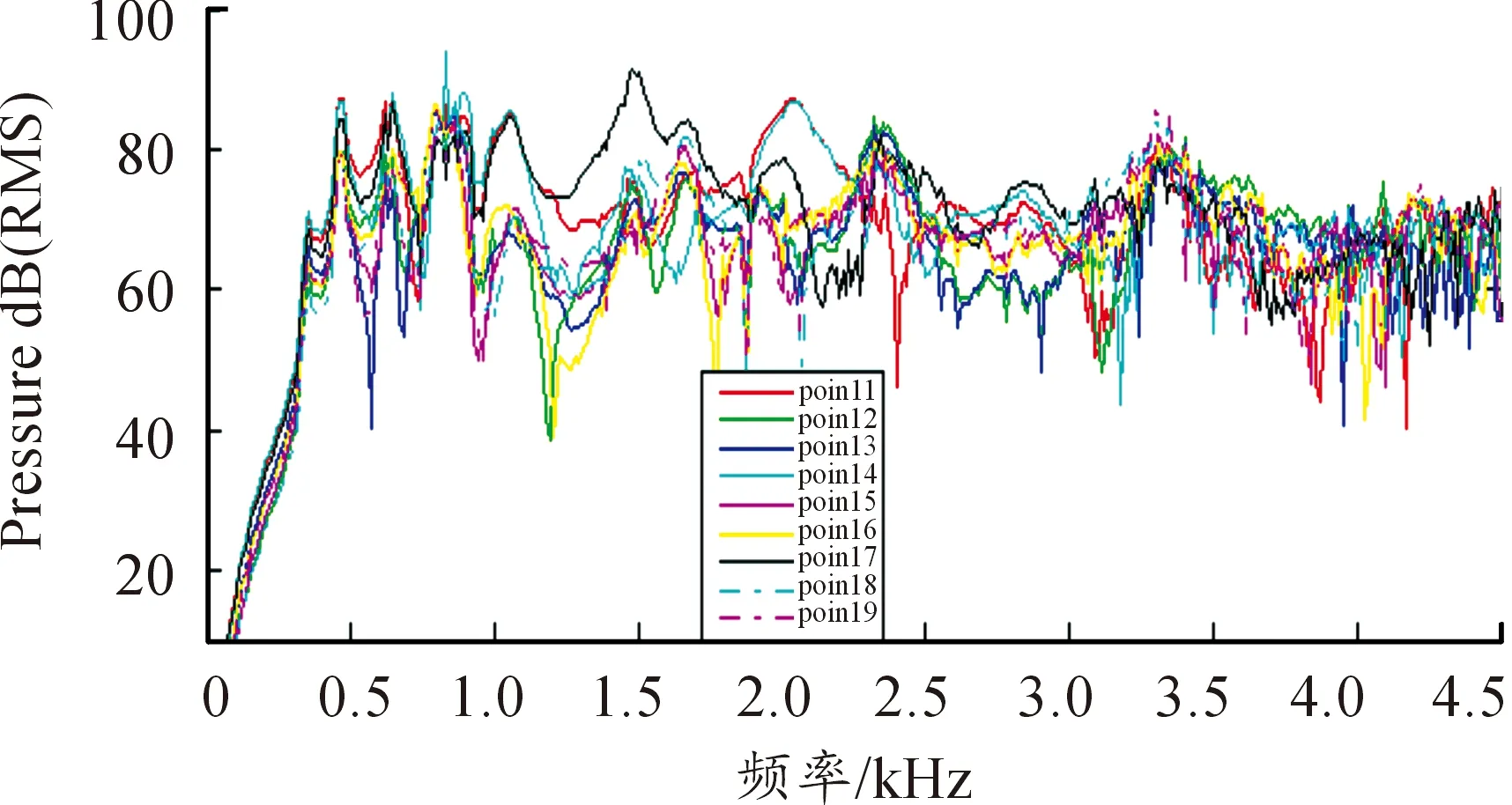
圖12 第1～9號場點聲壓-頻率譜

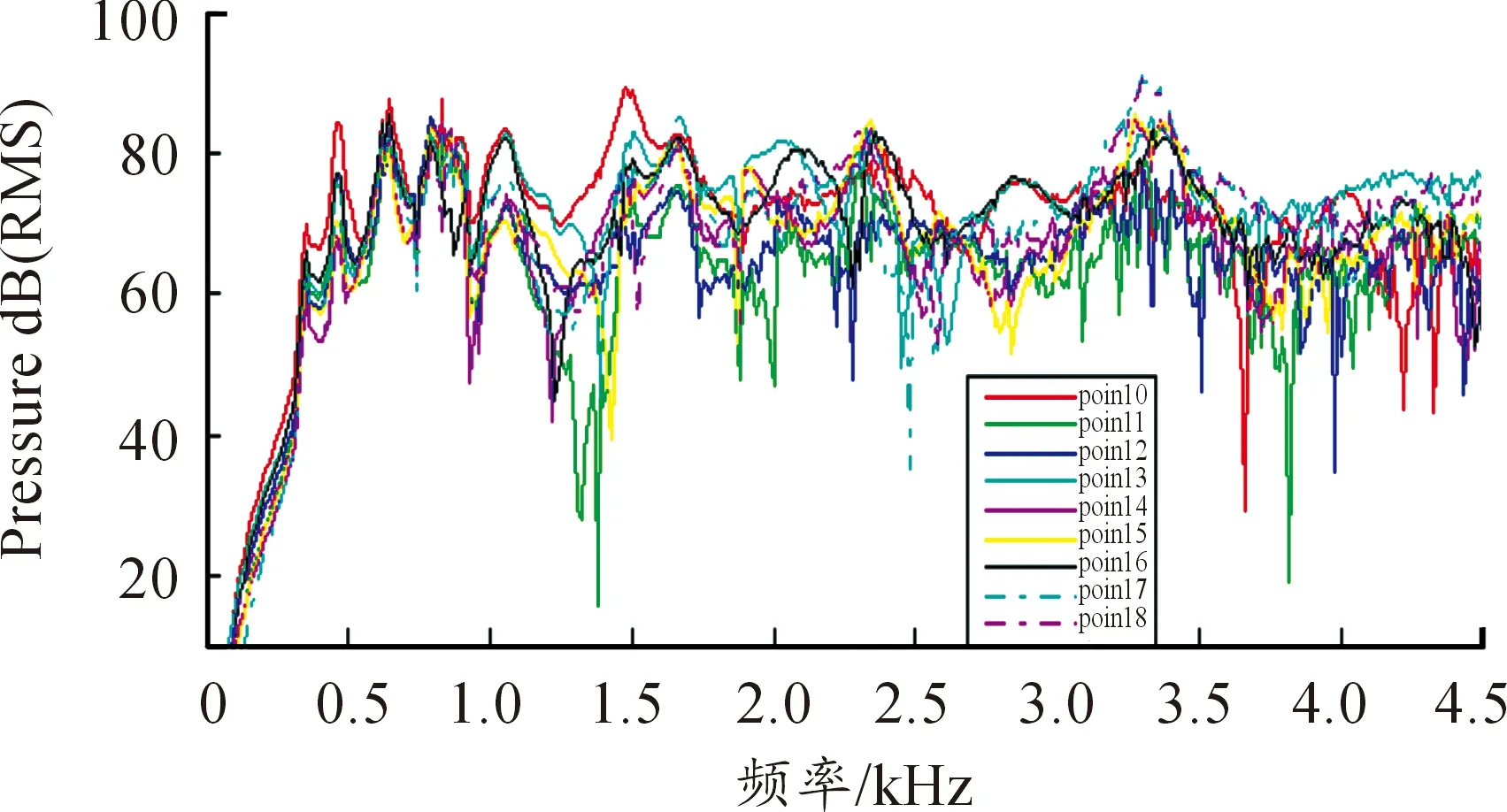
圖13 第10～18號場點聲壓-頻率譜

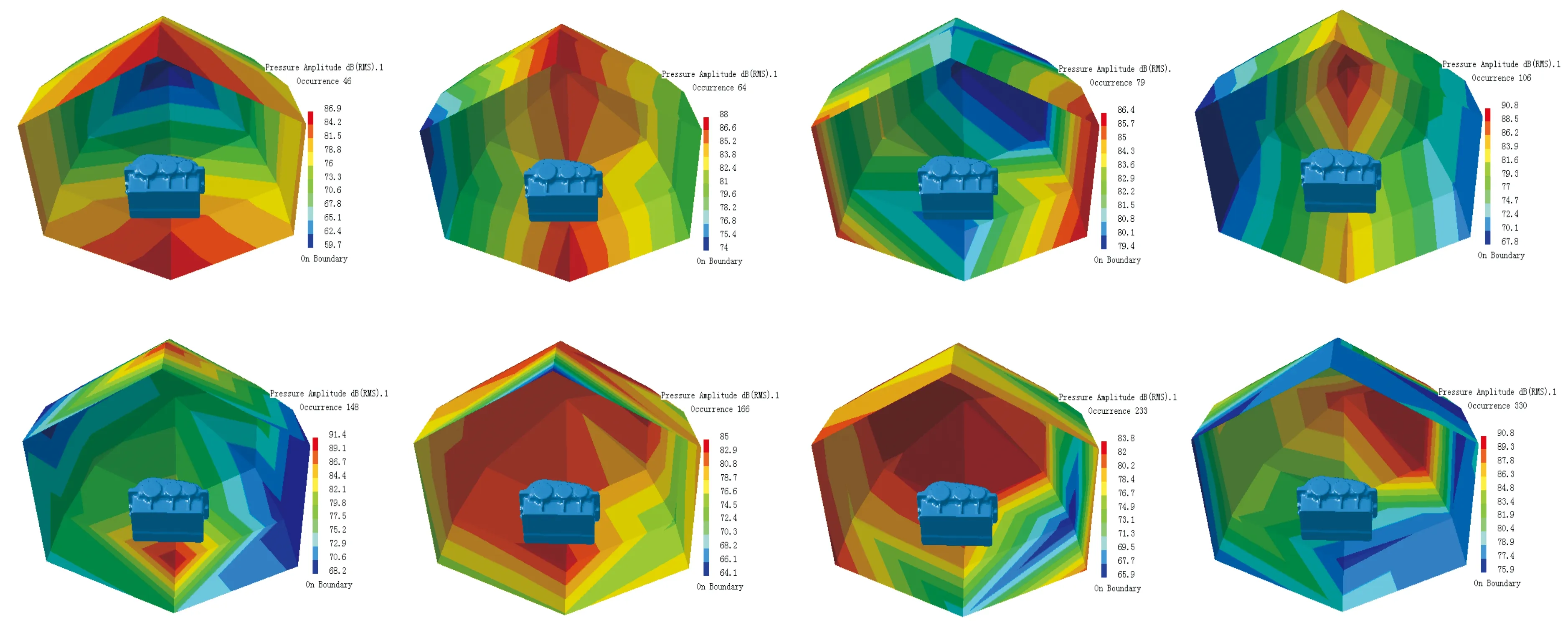
圖14 聲場聲壓分布云圖

總的來說，該減速器的噪聲輻射較大，如不加以優化，產品會有較大噪聲的風向，所以必須對其進行NVH性能優化。

5 減速器NVH性能優化

5.1 軸的優化

在齒輪-轉子系統中，從研究齒輪激勵入手，可以簡化成質量-彈簧振動系統，如圖15所示，K是等效彈簧剛度，M是等效質量。當質量塊振動時，傳遞到地面的力為F=Kx=Md2x/dt2，在相同的位移激勵下，等效剛度和等效質量越大，力就越大。所以可以通過減小軸的剛度，從而減小齒輪-轉子系統軸承作用力。

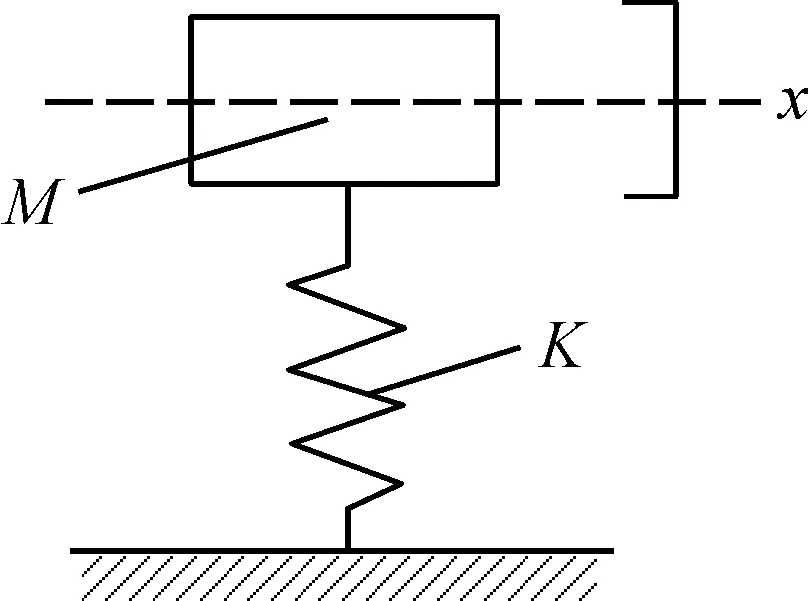
圖15 齒輪-轉子系統的簡化示意圖

本研究在滿足齒輪-轉子系統對軸強度要求的條件下，減小輸出軸和輸入軸的剛度。將第一級主動齒輪和軸承3之間修改成直徑20 mm、長94 mm和直徑35 mm、長6 mm的兩段。將第二級從動齒輪的固定臺階和軸承6之間修改成直徑46 mm、長10 mm和直徑35 mm、長61 mm。從結果看，第一級齒輪副傳動誤差增大而第二級齒輪副傳動誤差基本不變，如圖16所示，第一級齒輪的傳動誤差的最大最小值分別為-5.13 μm和-2.41 μm，相差2.72 μm，增加了54.5%，而第二級齒輪的傳動誤差的最大最小值分別為3.65 μm和3.12 μm，相差0.53 μm。這是由于減小軸的剛度使軸的靜態變形增大，從而影響齒輪副的嚙合狀態，造成傳遞誤差變大。圖17是未修改時軸承作用力和修改后軸承作用力的差值曲線，可以看出多數頻率下軸承作用力變化不大，在部分頻率范圍內既有大幅增大，也有大幅減小，這是修改軸后使系統的固有頻率移動造成的，總的來說軸承力變化不大。總之，修改軸使第一級齒輪副傳遞誤差增大，但軸承力變化不大，提高了通過齒輪修型減小軸承力的空間。

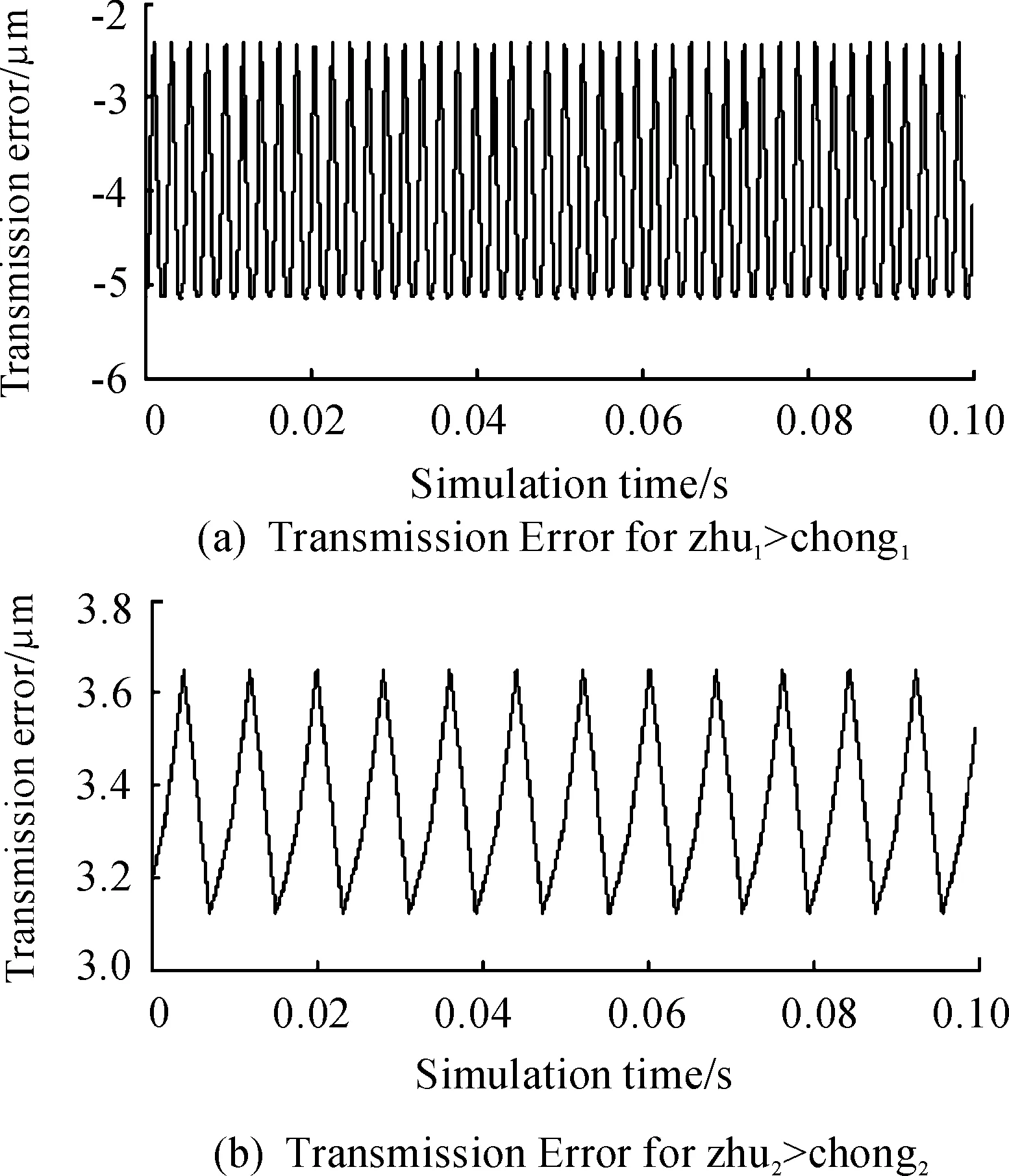
圖16 傳動誤差曲線

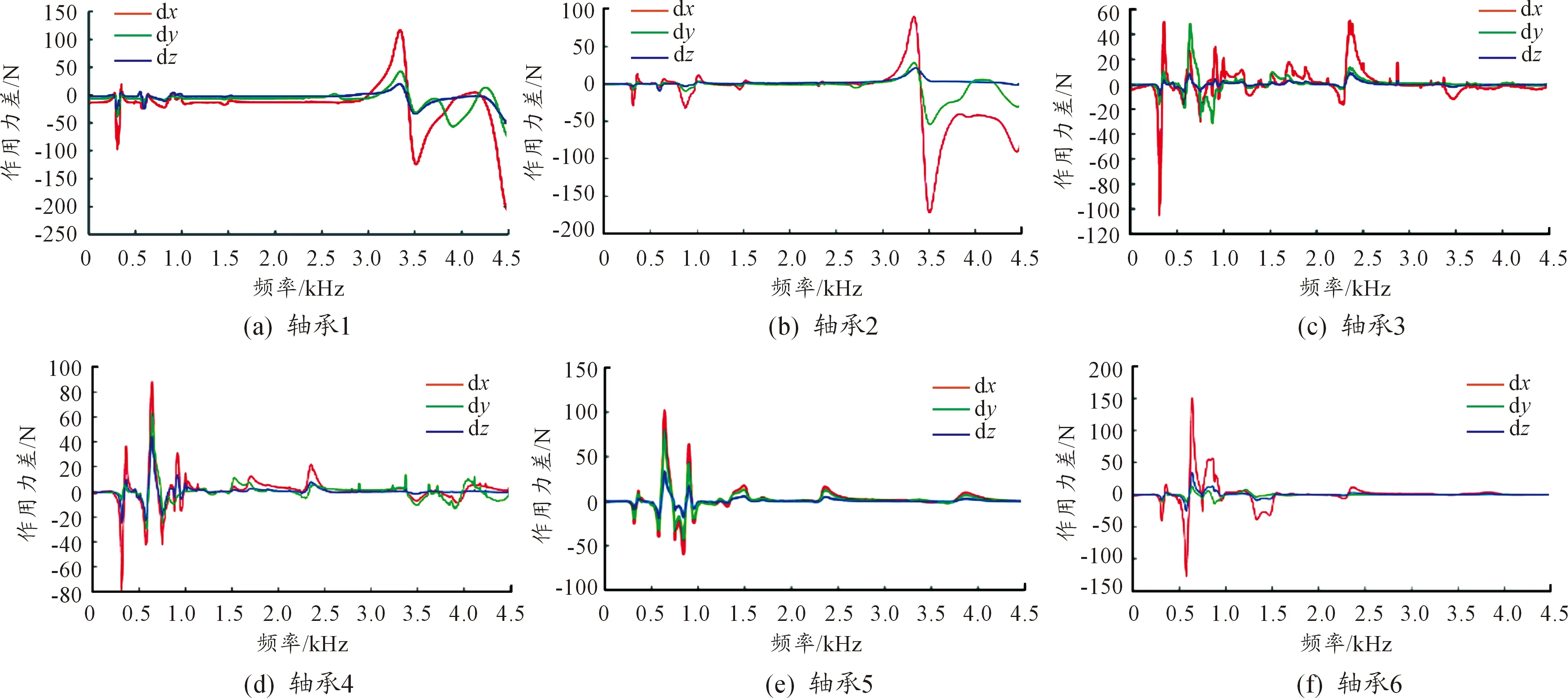
圖17 軸承作用力差值曲線

5.2 齒面的優化

齒面微觀修形是為了減小系統和輪齒變形引起的齒輪錯位，盡可能地使齒輪在發生接觸受載變形后，齒面壓力分布均勻，從而減輕齒面的偏載現象，保證輪齒受載變形后依然能夠相對平穩地傳遞力矩。從Romax齒輪載荷分析結果可以看出，修形前齒輪出現極其嚴重的偏載現象，低速端不承受載荷，而高速端載荷卻很高，因此必須對齒輪進行修形。

Romax軟件自帶的修形曲線有直線和拋物線，使用時不許手動確定修形曲線的具體形狀，只需在軟件中確定修形量、修形長度和響應的修形曲線類型。本文只對主動齒輪的嚙合面進行齒向修形，修形曲線為直線，第一級主動齒輪嚙合面修形量為20 μm、齒向傾度30 μm，第二級主動齒輪嚙合面修形量為215 μm、齒向傾度-10 μm。修形后齒輪載荷分布得到很大的改善、傳遞誤差也大大減低、軸承作用力也減小很多，優化結果如圖18所示。

5.3 殼體的優化

本研究對殼體進行三處局部優化，一是在箱體軸承座下方加橫向加強筋，二是在兩側的螺栓孔間增加一個螺栓孔，用于螺栓固定，三是在蓋板的下表面加加強筋。

本研究以5.2中得到的軸承作用力為激勵，分別計算優化前和優化后殼體的振動響應，取了三個測試點，分別為箱蓋上后端某處(1號測點)、箱體中間軸承座下方某處(2號測點)以及箱體底板面中間點(3號測點)。優化前和優化后殼體對應點的振動加速度差值曲線如圖19所示，除了1號測點由于移頻是某些頻率振動大幅度加強和減弱外，其余兩個測點的振動大大減弱，說明殼體的優化效果明顯。

5.4 優化后的聲輻射預測

采用5.1、5.2和5.3小節中所述的方法即軸-齒形-殼體綜合優化方法對減速器進行優化，優化后輻射聲功率譜曲線如圖20所示，聲功率的降低量曲線如圖21所示，在大部分頻率譜曲線下聲功率都大大減低，各峰值降低量分別為34.54 dB、28.12 dB、24.47 dB、13.68 dB、13.17 dB、18.87 dB以及11.48 dB。

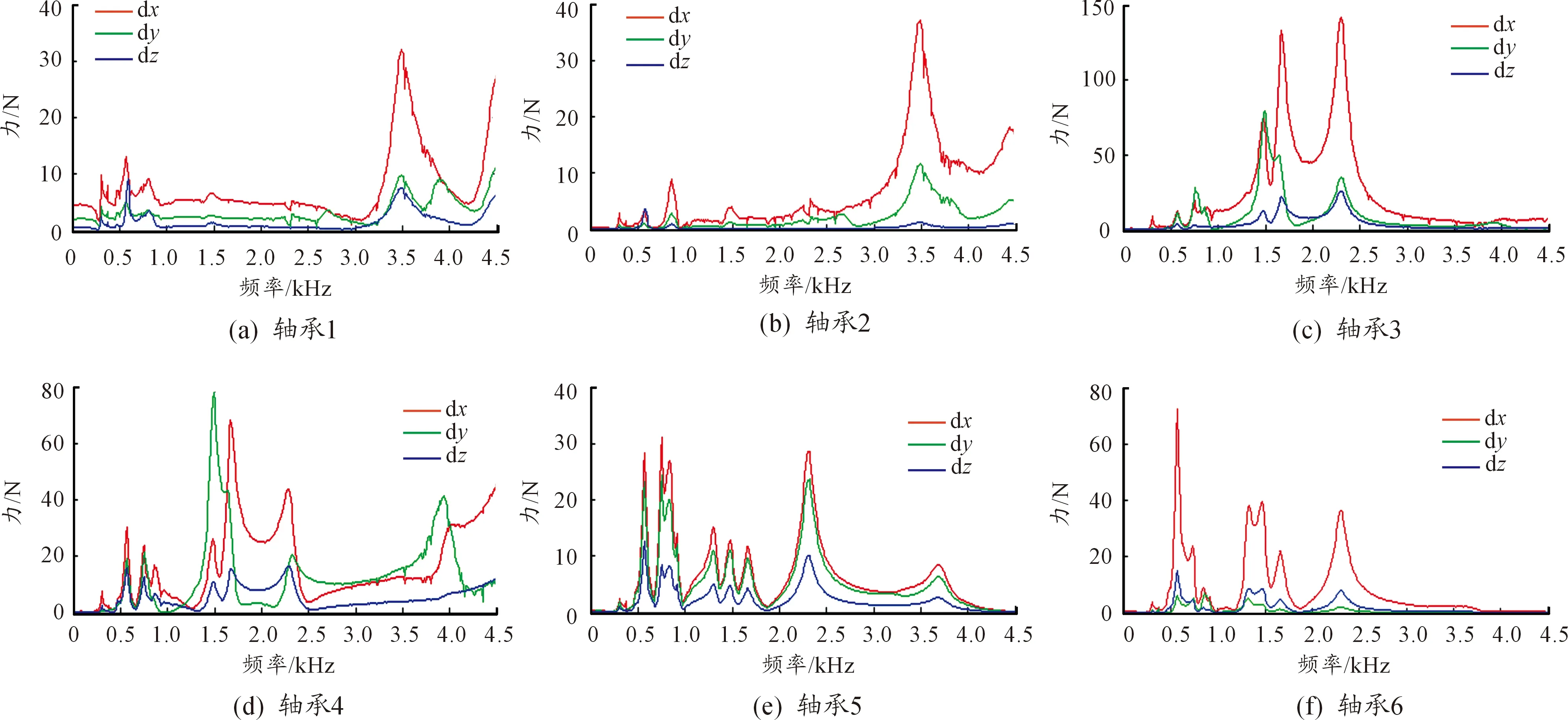
圖18 優化后軸承作用力曲線

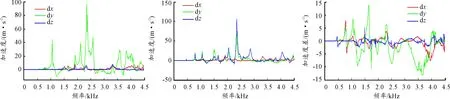
圖19 測點加速度差值曲線

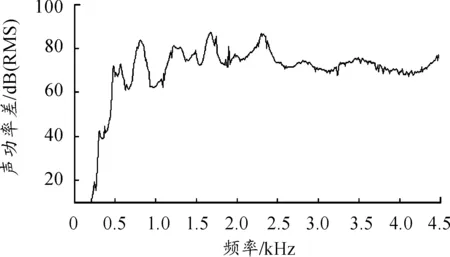
圖20 優化后聲功率譜曲線

6 結論

1) 齒輪副傳動誤差激勵引起振動，經齒輪、軸以及軸承傳遞到殼體上，齒輪-轉子系統的固有特性對振動的傳遞影響巨大；

2) 殼體的固有特性對殼體的振動和聲輻射影響深遠，而固定位置的選擇和數量對殼體的固有特性影響非常大；

3) 本文提出的軸-齒面-殼體綜合優化方法對降低減速器聲輻射、改善其NVH性能具有良好的效果，可成為齒輪傳動NVH設計的重要依據。