問題驅動 模型識別 揭示本質
——基于求解初中幾何最值問題的探究與思考

江蘇省太倉市第一中學 (215400)

朱建良

建構主義理論提出，學生的數學知識是意義建構的，而不是被動灌輸而成的．數學探究活動必須突出學生學習主體性，引導學生親歷體驗并參與探究過程，通過學生自主探索和思考，在數學建模、類比轉化等多方面得到進步和發展，從而提高探究活動的有效性．下面就初中幾何最值問題的教學實踐，談談如何通過建模教學，引導學生揭示幾何最值問題的內涵，疏理方法，理解幾何模型的深層意義，筆者意在拋磚引玉，以期廣大同行指正．

1.解讀問題，明確目標

1.1 疏理結構，探究特征

以蘇科版義務教育《數學》九年級教材為學習內容，探究初三幾何最值問題為主題，解讀教材內容．在平面幾何問題中，當某幾何元素在給定條件變動時，求某幾何量(如線段的長度、圖形的面積、角的度數)的最大值或最小值問題，稱為幾何最值問題．解決幾何最值問題時應用幾何性質有：(1)三角形的三邊關系：兩邊之和大于第三邊，兩邊之差小于第三邊；(2)兩點間線段最短；(3)連結直線外一點和直線上各點的所有線段中，垂線段最短；(4)定圓中的所有弦中，直徑最長等．

幾何最值問題是初中數學學習的一個難點，考查了學生的邏輯思維能力和空間觀念，學生對此類問題往往感覺無從下手，找不到適當的切入點，導致思維阻滯，通過本課例的探究，嘗試以數學建模為解決問題的突破口，基于問題解決，設計問題串展開探究學習，滲透“數形結合”、“類比”等數學思想，幫助學生揭示幾何圖形變換的規律、積累解決問題的策略，提升學生解決問題的能力．

1.2 理解問題，凝聚思想

求線段和的最值類問題的探究思路在于：通過平移、旋轉及軸對稱等圖形變化轉化為求兩點之間或者點到直線之間的最短距離問題．此類問題的幾何圖形變換，往往改變了特殊點的位置，不改變形狀和大小，可以通過建模，優化圖形結構，整合圖形信息，使復雜問題更直觀、簡潔．如遇涉及生活實際問題，可以通過對實際問題的分析、嘗試，構建起相關幾何模型，引導學生在質疑探究中感悟領略建模的思想和方法，提升學生的抽象、概括和演繹推理能力．

1.3 提煉模型，形成方法

基本模型1 在直線l上求一點P，使線段PA+PB最短．

如圖1，作點A關于直線l的對稱點A′，連接A′B交直線l于點P，∵PA=PA′，∴PA+PB=PA′+PB=A′B．此時，線段A′B最短．

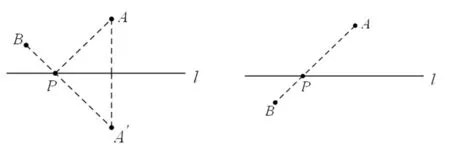
圖1 圖2

基本模型2 如圖2，當A、B兩點位于直線l的異側時，連接AB交直線l于點P，AP+BP=AB.此時，線段AB最短．

基本模型3 如圖3，⊙O中過圓內一點P的最長弦是直線AB，當弦CD⊥AB于點P時，弦CD是過點P最短的弦．

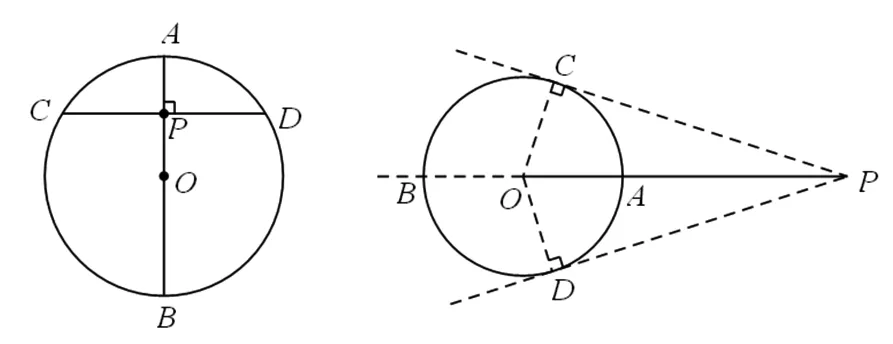
圖3 圖4

基本模型4 如圖4，⊙O外一點P與⊙O上的點連接的線段中，PA最短，PB最長，當⊙O動點與點P的連線PO構成的角的度數最大時，有PC、PD與⊙O相切的位置．

2.凸現主體，回歸模型

2.1 問題驅動，引領思維

數學模型描述了各變量間內的數量和位置關系，是指反映特定問題的數學關系結構，幾何最值問題學習內容通過數學建模來表達和體現，把數學模型看做是幾何知識的起點和主線．探究建模，不是簡單地對數學公式、定義、定理、公理等逐條羅列，而是挖掘一組問題包含的數學模型，通過建模解決問題達到建構內化知識結構的目的．

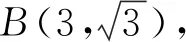
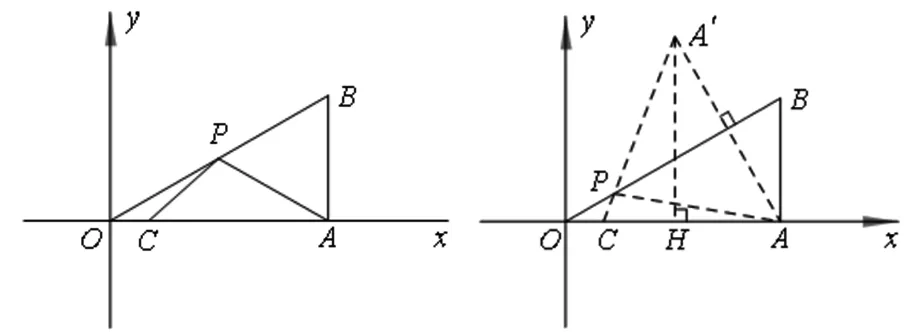
圖5 圖6

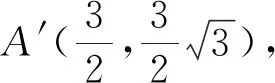
2.2 合理設計，強化聯系

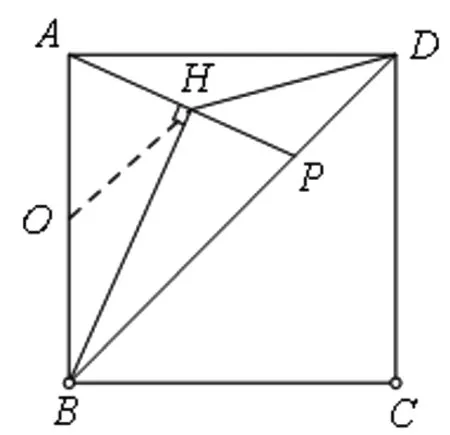
圖7

拓展1 如圖7，點P是正方形ABCD的對角線BD上的一個動點(不與B、D重合)，連接AP，過點B作直線AP的垂線，垂足為H，連接DH，若正方形的邊長為4，求線段DH長度的最小值．

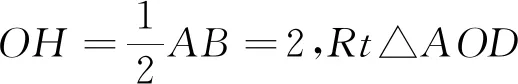
2.3 關注生成，優化策略

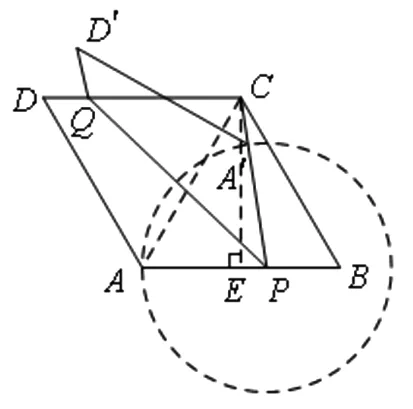
圖8

拓展2 如圖8，菱形ABCD的邊AB=8，∠B=60°，P是AB上一點，BP=3，Q是CD邊上一動點，將梯形APQD沿直線PQ折疊，A的對應點為A′，當CA′的長度最小時，求CQ長度．

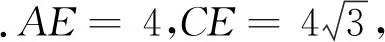
3.追根溯源，積累經驗

3.1 動態探究，尋求本質

數學建模的目的指向探究幾何最值問題的本質，通過動態變換建模求解，引導學生獲得一些關于幾何最值知識或者建模技能和“基本經驗”，在動態變化過程中尋求不變規律，在感性認識到理性認識的體驗過程中積累基本的活動經驗．

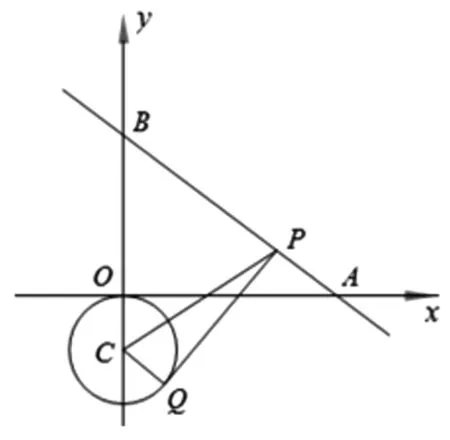
圖9

3.2 變式拓展，活化思維

變式1 如圖10，在平面直角坐標系xOy中，分別以點A(2,3)，B(3,4)為圓心，以1,3為半徑作⊙A，⊙B，點M，N分別是⊙A，⊙B上的動點，點P為x軸上的動點，求PM+PN最小值．

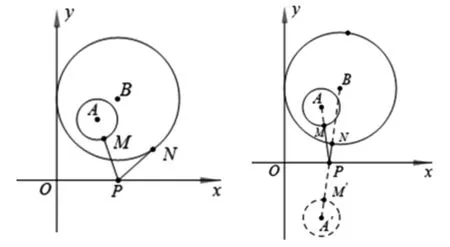
圖10 圖11

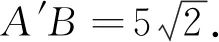
3.3 變式感悟，發展能力

變式2 如圖12，已知A、B兩點的坐標分別為(2,0),(0,2)，⊙C的圓心坐標為(-1,0)，半徑為1，D是⊙C上的一個動點，線段DA與y軸將交于點E，求△ABE面積的最小值．

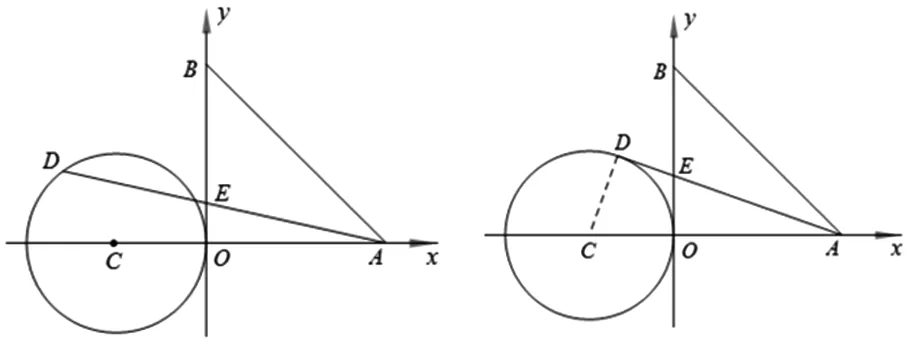
圖12 圖13

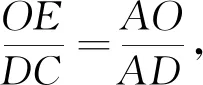
4.反思結構，優化方法

將幾個背景相似、角度不同，但又在建模方法和解題技巧等方面具有相似性或有內在聯系的幾個最值問題組合在一起，作為一個幾何最值問題系列展開探究，反思歸納，通過拓展問題，上升到思想方法的層面上去發展學生的思維能力．

拓展在直角坐標系中，已知點A(3,2),B(1,5)，(1)若點P坐標為(0,m)，問m為何值時，△PAB的周長最短，并求出△PAB的周長；(2)若點C、D的坐標分別為C(0,a)，D(0,a+4)，問a為何值時，四邊形ABCD的周長最短，并求出此時的周長．

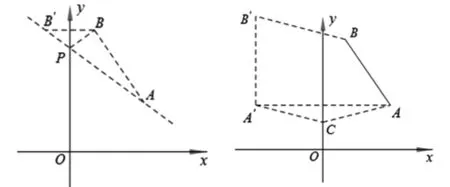
圖14 圖15

(2)如圖15，作A點關于y軸的對稱點A′，點A′(-3,2)，作A′B′∥y軸，取A′B′=CD=4，有B′(-3,6)，連接BB′交y軸于點D，∵A′B′∥CD，且A′B′=CD，有A′B′DC，直線BB′解析式為得此時四邊形ABDC周長最短，為

5.解法自然，通性通法

設計問題對幾何最值問題從不同角度、不同情形、不同層次做出有效變化，使幾何最值問題的條件、結論及形式發生變化，以探究的變式問題為思維的載體，引導學生自覺體驗幾何模型的形成過程、邏輯推導過程和類比拓展提升過程．

變式如圖16，在平面直角坐標系中，A(-4,0),B(0,4)，點C、D分別為OA、OB的中點，若正方形OCED繞點O順時針旋轉，得到正方形OC′E′D′，記旋轉角為α(0<α<360°)，連接AC′，BD′，設直線AC′與BD′相交于點F，求點F的縱坐標的最大值．

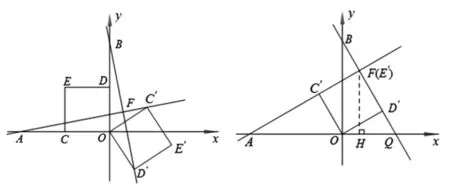
圖16 圖17

《數學課標(2011版)》中倡導“讓學生獲得廣泛的數學活動經驗”．學生數學學習的本質是學生自主建構自己對數學知識理解的過程，學生的學習過程是真正意義上的再創造過程．

探究幾何最值問題，既要學會構圖，循點覓形，生長圖形，在動態變化中整體把握圖形間的聯系，提煉出基本模型，化繁為簡，模型引領，揭示幾何最值問題的本質屬性．

求解幾何最值問題是要順著問題解決的脈絡，引導學生從問題解決中建立幾何模型解決問題，再從問題解決后自己產生新問題，再質疑，變式拓展，解一題，連一片，通一類，通過“螺旋遞進式”的探究培養學生的問題意識，提升學生靈活解決問題的能力，進而體會探究數學問題的無窮樂趣，體悟成功的喜悅．