剛性彈體斜侵徹貫穿混凝土靶的姿態偏轉理論模型*

段卓平，李淑睿，馬兆芳，歐卓成，黃風雷

（1. 北京理工大學爆炸科學與技術國家重點實驗室，北京 100081；

2. 北京理工大學珠海學院，廣東 珠海 519088）

彈體斜侵徹貫穿混凝土靶一直是侵徹領域的熱點。實際情況下，由于彈體所處環境和受力情況非常復雜，彈體著靶時會與靶板法線存在一定角度，當混凝土靶板厚度有限時，彈體會貫穿靶板，同時反射形成的拉伸波會在背靶面造成一定厚度的崩落[1]。實驗研究[2-5]發現,在斜侵徹過程中彈體姿態會發生一定程度的偏轉，偏轉程度受彈體著靶初速、著靶角等多種因素影響，為定量描述這些因素對彈體姿態偏轉的影響，并預測斜侵徹貫穿混凝土靶時彈體姿態變化，需結合實驗研究發展相應的理論模型。

Chen 等[6]建立了剛性彈體斜侵徹貫穿混凝土靶的三階段理論模型，將剛性彈體斜侵徹貫穿混凝土靶的過程分為了初始開坑、隧道和剪切沖塞三個階段，同時提出了斜錐形剪切沖塞塊假設，并利用無量綱量沖擊函數I 和彈體形狀函數N[7-8]分析了彈體的姿態偏轉。然而該模型假定彈體僅在初始開坑階段發生偏轉，而在隧道階段和剪切沖塞階段彈體姿態不再改變，因此該模型得到的彈體姿態角（即彈體軸線與靶板表面外法線之間的夾角）的變化趨勢是增大的。但是彈體斜侵徹貫穿混凝土薄靶實驗所得彈體的出靶姿態角是減小的[9-10]，由于開坑階段彈體有跳彈趨勢，彈體姿態角一定增大[11-12]，因此在剪切沖塞階段彈體姿態再次發生了偏轉，則該模型中關于剪切沖塞段彈體姿態不變的假設與實際不符。同時，在彈體斜侵徹貫穿多層間隔混凝土靶實驗中得到的靶板背面的破壞形狀是以彈洞為圓心近似為對稱圓形[10]，并非Chen 等[6]提出的不對稱斜錐形彈坑。另外該模型僅根據開坑深度將混凝土靶分為薄靶和厚靶，忽略了這兩者之間的中厚靶情況，從而限制了模型的適用范圍，因此Chen 等[6]的彈體斜侵徹貫穿混凝土靶的模型存在一定問題，需要進一步修正。

本文中基于Chen 等[6]的三階段理論模型，根據實驗現象重新假設沖塞塊形狀，且在彈體貫穿出靶的剪切沖塞階段引入彈體姿態二次偏轉機制，并考慮彈體轉動慣量對姿態偏轉的影響，通過分析不同階段的彈體運動狀態，從而建立適用范圍更廣、更符合實際的彈體斜侵徹貫穿混凝土靶的姿態偏轉理論模型，同時提出明確的混凝土靶厚分類方法，通過計算結果與實驗數據的對比驗證本文模型預測彈體姿態變化的有效性。

1 理論模型

理論模型的建立基于以下假設條件：（1）彈體為剛體，在混凝土靶體內部做剛體平面運動；（2）混凝土靶體為均質各向同性材料，忽略其中鋼筋和骨料結構的影響；（3）混凝土對彈體的阻力作用在彈頭部。

不考慮彈體攻角對彈體姿態的影響，僅關注侵徹過程中彈體姿態角β（彈體軸線與靶體表面外法線之間的夾角）的變化，并定義彈體姿態偏轉角Δβ 為侵徹過程中彈體瞬時姿態角與彈體初始姿態角之間的差值，Δβ 的符號表示彈體姿態的偏轉方向，為正時表示彈體姿態向著姿態角變大的方向偏轉，為負時表示彈體姿態向著姿態角變小的方向偏轉。

設彈體斜侵徹貫穿混凝土靶時，彈體著靶初速為v0，初始姿態角為β0。如圖1 所示，彈體直徑為d，彈長為L，彈體質心C 距彈尖的距離為lC，彈頭長度為h，混凝土靶體厚度為H。彈體的斜侵徹貫穿過程可分為初始開坑、隧道和剪切沖塞三個階段[6]，本文中認為彈體在初始開坑階段和剪切沖塞階段均會發生姿態偏轉，且偏轉方向相反，即在初始開坑階段彈體姿態發生偏轉且彈體姿態角β 變大（Δβ 值為正），隧道階段彈體姿態不偏轉（Δβ=0），剪切沖塞階段彈體姿態再次偏轉且彈體姿態角β 變小（Δβ 值為負）。

1.1 初始開坑階段

在初始開坑階段，彈體的運動微分方程為：

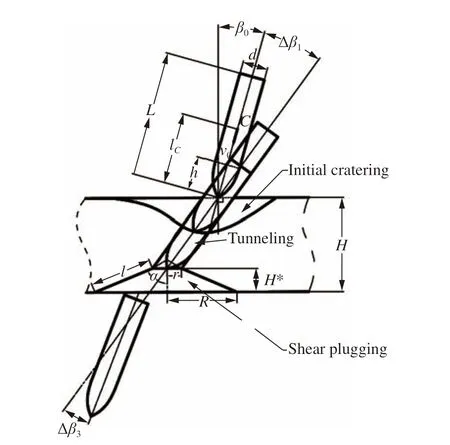
圖 1 彈體斜侵徹貫穿混凝土靶過程中各階段彈體姿態偏轉過程示意圖Fig. 1 Illustrated attitude deflection of the projectile in each stage during the oblique perforation of concrete targets

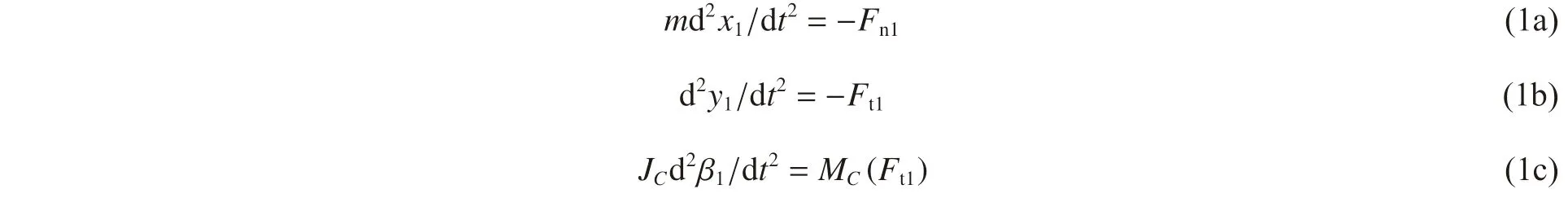
式中：彈體軸向合阻力Fn1、橫向合阻力Ft1以及過質心C 的轉動力矩MC(Ft1)滿足下式[6,13]：

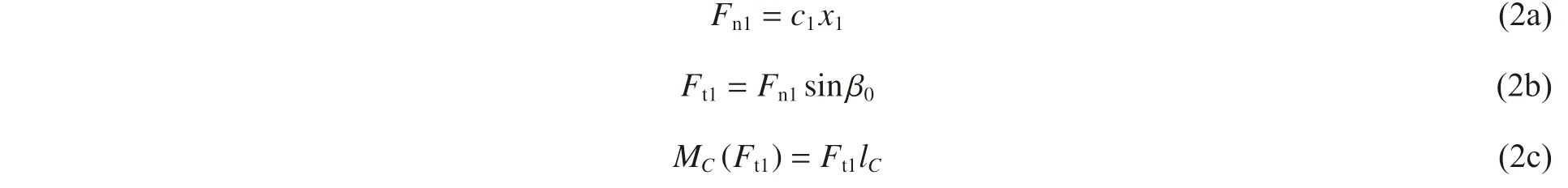
式中：m 為彈體質量，x1和β1分別為彈體的瞬時侵徹行程和瞬時姿態角，JC為彈體繞垂直彈道平面且穿過質心C 的轉軸的轉動慣量，c1為初始開坑階段的阻力常數。開坑階段開始瞬時t = 0，彈體侵徹行程X01= x1(0) = 0，速度V01= v1(0) = v0，角速度Ω01= ω1(0) = 0，姿態角B01= β1(0) = β0。聯立式(1)～(2)，由彈體速度v1= dx1/dt、彈體角速度ω1= dβ1/dt，利用前述初始條件，則可解得初始開坑階段彈體瞬時侵徹行程x1、瞬時速度v1和瞬時姿態角β1的表達式。設初始開坑階段結束瞬時t = T1，彈體侵徹行程X1= x1(T1)，速度V1= v1(T1)，彈體姿態角B1= β1(T1)，彈體姿態偏轉角為Δβ1= B1- B01，則得關系式（阻力常數c1、時間T1需通過聯立方程組求解）：

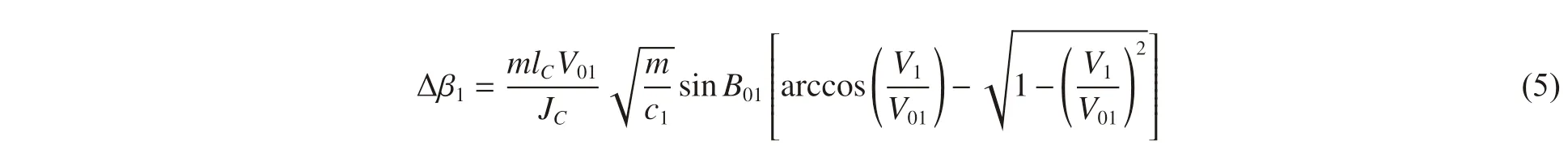
1.2 隧道階段

隧道階段開始瞬時t = T1，彈體侵徹行程X02= x2(T1) = 0，彈體速度V02= v2(T1) = V1，彈體姿態角B02=B1。設隧道階段結束瞬時t = T2，彈體侵徹行程X2= x2(T2)，彈體速度V2= v2(T2)，由于該階段彈體橫向阻力對稱，彈體姿態不偏轉，則彈體姿態角B2= β2(T2) = B1= β0+Δβ1，彈體姿態偏轉角Δβ2= 0。該階段彈體軸向合阻力Fn2滿足關系式[13]式中：S 為經驗常數，與混凝土無側限抗壓強度fC相關；N*為彈頭形狀系數，ρ 為混凝土靶體密度。利用牛頓第二定律并對式(6)進行積分，可得隧道階段彈體侵徹行程X2為：

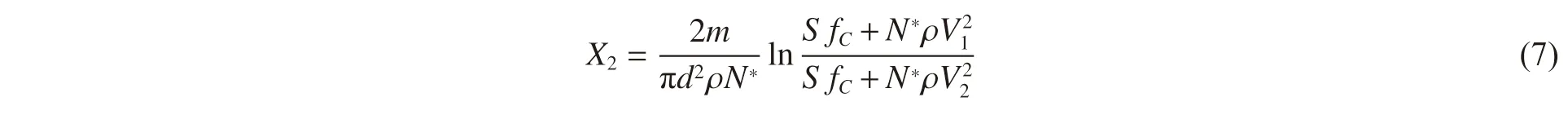
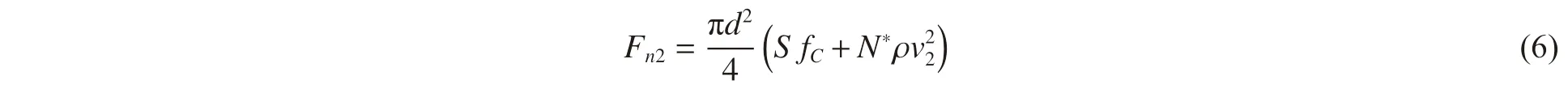
1.3 剪切沖塞階段

將沖塞塊形狀近似假設為錐形圓臺，并取沖塞塊的坡度角α=66.1°[14]，如圖1 所示。利用圖1 中的幾何關系可得錐形圓臺剪切沖塞塊的側面積As滿足關系式：Ascosα = πdH*[sec(β0+Δβ1)+(H*/d)tanα]，H*為剪切沖塞塊厚度，因此剪切沖塞塊形成瞬時彈體所受軸向合阻力Fns的表達式為[6]：

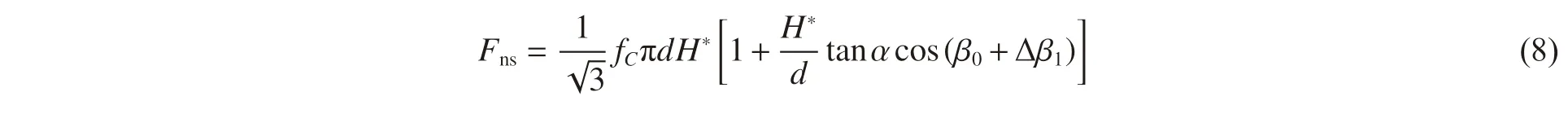
剪切沖塞階段彈體姿態的偏轉方向與初始開坑段相反，則該階段彈體的運動微分方程為：

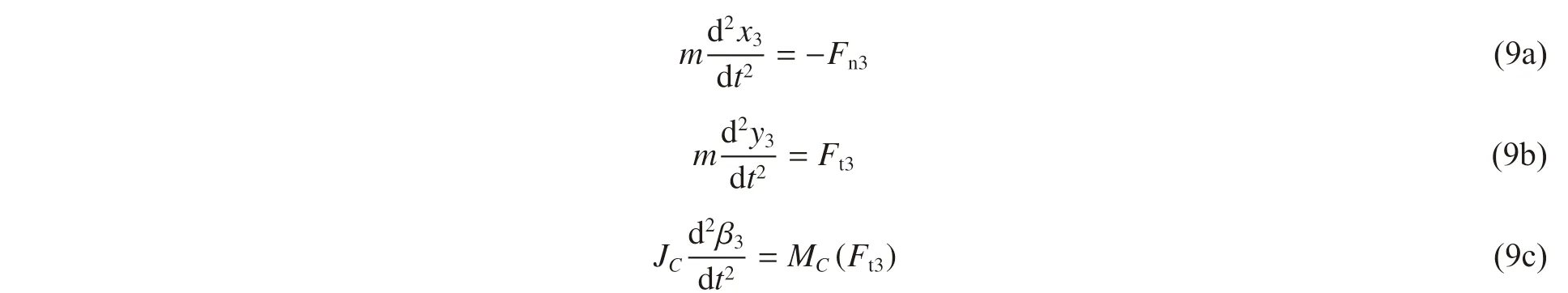
其中：

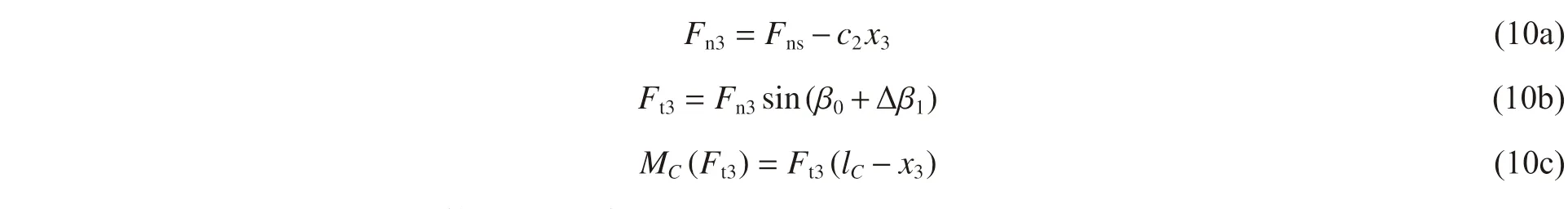
設剪切沖塞階段隨著彈體運動，彈體橫向合阻力Ft3的作用位置由彈尖逐漸向彈身方向移動，軸向合阻力Fn3由該階段開始瞬時的Fns逐漸線性遞減為0，如式(10a)所示，其中c2為剪切沖塞段的阻力常數，且Ft3與Fn3始終滿足關系式(10b)[6]。設使彈體姿態偏轉的力臂l 隨彈體侵徹行程x3線性變化l=lC-x3，則轉動力矩MC(Ft3)如式(10c)所示。

設剪切沖塞階段開始瞬時t = T2，彈體侵徹行程X03= x3(T2) = 0，彈體速度V03= v3(T2) = V2，彈體角速度Ω03= ω3(T2) = 0，彈體姿態角B03= β3(T2) = B2= β0+ Δβ1。聯立式(9)～(10)，利用前述初始條件，可解得剪切沖塞段彈體瞬時侵徹行程x3、瞬時速度v3、瞬時加速度a3以及瞬時姿態角β3的表達式。

當彈體運動到某一位置時，彈體與沖塞塊分離，彈靶之間再無作用力（不考慮分離再接觸），則此時彈體加速度為零。設此瞬時即為剪切沖塞階段結束瞬時t = T3，且此時彈體侵徹行程X3= x3(T3)，速度V3=v3(T3)，加速度a3=0，角速度Ω3= ω3(T3)，姿態角B3= β3(T3)，彈體姿態偏轉角Δβ3= B3-B03，則得關系式（阻力常數c2需通過聯立方程組求解）：

2 斜侵徹貫穿不同厚度混凝土靶

彈體斜侵徹貫穿不同厚度混凝土靶的姿態變化與靶體厚度有關，不同靶厚下彈體的姿態偏轉過程如圖2 所示。

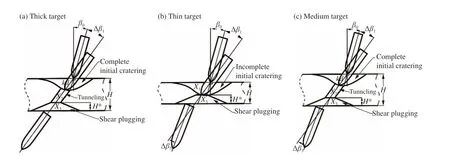
圖 2 彈體斜侵徹貫穿不同厚度混凝土靶時彈體姿態的偏轉過程Fig. 2 Attitude deflection of the projectile in oblique perforation of concrete targets with different thickness.

2.1 厚靶

彈體斜侵徹貫穿混凝土厚靶時彈體姿態的偏轉過程如圖2(a)所示，包括完全開坑階段、隧道階段和剪切沖塞階段[6]。由于隧道段足夠長，能夠完全阻滯彈體的橫向運動，因此彈體姿態在剪切沖塞階段不偏轉(Δβ3=0)，僅在開坑階段發生一次偏轉，則彈體出靶時姿態角為β0+Δβ1。

完全開坑時彈體的侵徹行程X1= kd，其中k = 0.707 + h/d 為無量綱侵徹經驗深度[8]。由于完全開坑階段結束瞬時即為隧道階段開始瞬時，此時彈體軸向合阻力Fn1= Fn2，利用式(2a)與式(6)，并聯立式(3)～(5)，通過求解方程組即可得到完全開坑階段結束瞬時的T1、彈體速度V1和彈體姿態偏轉角Δβ1以及開坑階段阻力常數c1：

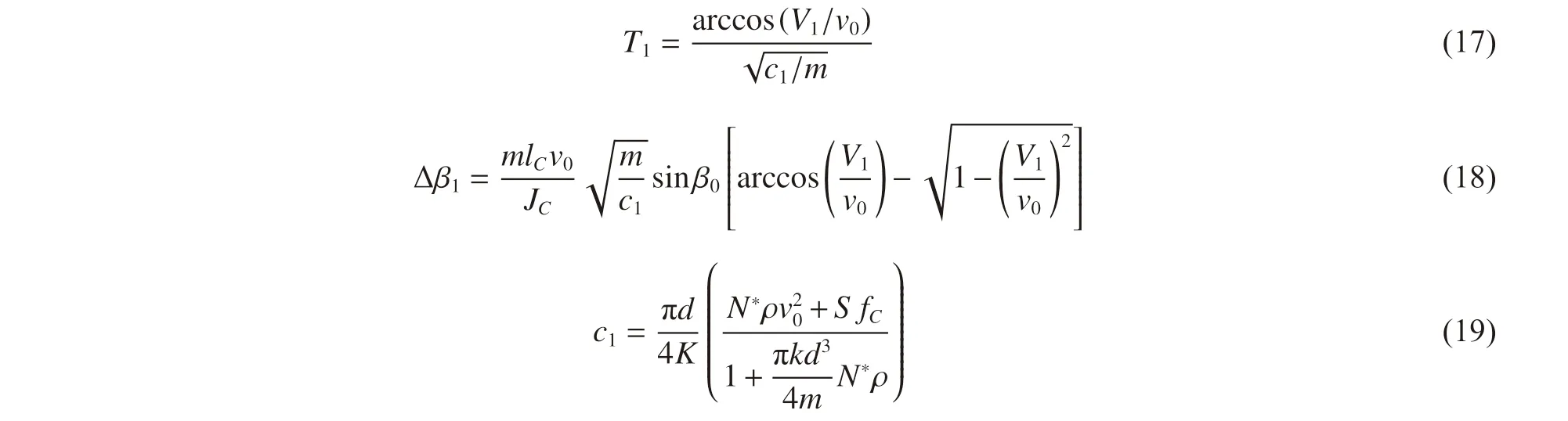
由圖2(a)可得彈體隧道區行程和剪切沖塞段行程分別滿足關系式：

由于隧道階段結束瞬時即為剪切沖塞階段開始瞬時，此時彈體軸向合阻力Fn2=Fn3，利用式(6)、(8)，并聯立式(7)、(11)～(13)與(20)～(21)，將式(7)中的ln 函數進行一階Taylor 展開，通過求解方程組即可得到彈體侵徹行程X2和X3、彈體速度V2和V3、剪切沖塞階段結束瞬時的T3，以及剪切沖塞段的阻力常數c2和剪切沖塞塊厚度H*。

2.2 薄靶

彈體斜侵徹貫穿混凝土薄靶時彈體姿態的偏轉過程如圖2(b)所示，僅包括不完全開坑階段和剪切沖塞階段[6]、無隧道階段，因此彈體姿態會在開坑階段和剪切沖塞階段發生兩次偏轉，且偏轉方向相反，則彈體出靶時姿態角為β0+Δβ1+Δβ3。

由圖2(b)可得彈體初始開坑段和剪切沖塞段的侵徹行程X1和X3分別滿足關系式：

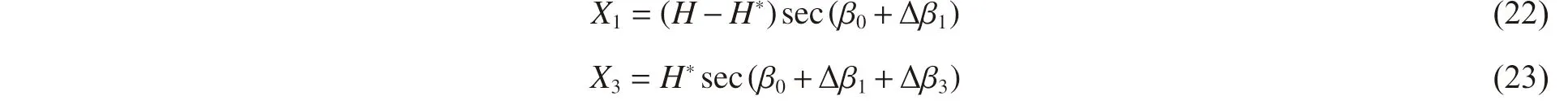
由式(19)可知，阻力常數c1與開坑階段的侵徹深度無關，因此式(19)也適用于不完全開坑。由于開坑階段結束瞬時即為剪切沖塞階段開始瞬時，此時彈體軸向合阻力Fn1=Fn3，利用式(2a)、(8)，并聯立式(3)～(5)、(11)～(15)與(22)～(23)，求解方程組即可得到彈體不完全開坑階段結束瞬時T1和剪切沖塞段結束瞬時T3、彈體侵徹行程X1和X3、彈體速度V1和V3、彈體姿態偏轉角Δβ1和Δβ3、彈體角速度Ω3，以及剪切沖塞段阻力常數c2和剪切沖塞塊厚度H*。

2.3 中厚靶

彈體斜侵徹貫穿混凝土中厚靶時彈體姿態的偏轉過程如圖2(c)所示，包括完全開坑階段、隧道階段和剪切沖塞階段。但由于隧道區長度有限，不能完全阻滯彈體的橫向運動，彈體姿態在剪切沖塞階段仍會發生偏轉，因此彈體出靶時姿態角為β0+Δβ1+Δβ3。

利用隧道階段結束瞬時的彈體速度V2以及隧道段長度X2，假設該彈體以v0t的初速侵徹一虛擬薄靶，令其完全開坑段結束瞬時的彈體速度V1t=V2，則可利用式(16)反推得彈體初速v0t。引入修正系數δx描述彈體斜侵徹貫穿中厚混凝土靶時隧道長度對剪切沖塞段彈體姿態偏轉角的影響，其表達式為：

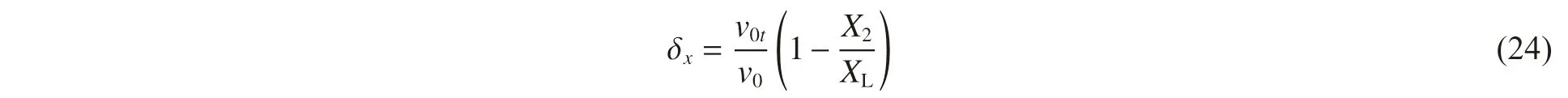
式中：XL為臨界隧道區長度，即能夠完全阻滯彈體橫向運動、使得彈體姿態在剪切沖塞階段不發生偏轉（即Δβ3=0）的最短隧道長度。若彈體長徑比L/d＞4，XL可取經驗值XL=2d。利用式(14)～(15)，則彈體斜侵徹貫穿混凝土中厚靶時剪切沖塞階段結束瞬時的彈體姿態偏轉角Δβ3和彈體角速度Ω3為：

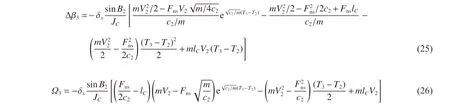
2.4 靶厚分類

根據彈體侵徹過程中是否存在隧道段區分薄靶和非薄靶，設HL為臨界靶厚，即彈體斜侵徹貫穿靶厚為HL的靶板時僅經歷完全開坑和剪切沖塞兩個階段，無隧道階段。因此當靶體厚度H＜HL時彈體侵徹過程不含隧道段，則靶體為薄靶；當H＞HL時彈體侵徹過程存在隧道段，則靶體為非薄靶。若彈體的幾何形狀、彈體和混凝土靶體的材料參數以及彈靶關系確定，則對應有唯一的臨界靶厚HL，可參考上述分析過程通過求解方程組得到。

由于彈體斜侵徹貫穿混凝土厚靶時隧道區足夠長，彈體在剪切沖塞階段不發生偏轉；而斜侵徹貫穿中厚靶時隧道區長度有限，彈體在剪切沖塞段仍會再次偏轉。因此本文中利用隧道區長度X2與臨界隧道區長度XL區分混凝土中厚靶和厚靶，即當0 ＜X2＜XL時，靶體為中厚靶；當X2≥ XL時，靶體為厚靶。

3 模型驗證

Hanchak 等[15]利用實驗手段測得了不同初速下彈體垂直侵徹48 MPa 普通強度鋼筋混凝土靶體的出靶剩余速度，其中混凝土靶體強度為48 MPa，混凝土密度為2 440 kg/m3，靶板厚度為0.127 m。實驗所用彈體為尖卵形彈頭，彈體質量為0.5 kg，彈體直徑為0.025 4 m，CRH(caliber-radius-head)=3。如表1 所示，本文中模型的計算結果與實驗數據之間的相對誤差均在18%以內，表明本文模型可以較準確地預估彈體垂直侵徹貫穿混凝土靶的出靶剩余速度。

在彈體斜侵徹貫穿多層間隔混凝土薄靶的實驗研究中，馬兆芳等[10]利用高速運動分析系統記錄的彈體彈道偏轉過程顯示每層靶體的彈體出靶姿態角均小于入靶姿態角，即彈體姿態向著姿態角減小的方向發生了偏轉，因此實驗測得的彈體姿態偏轉角（彈體出靶姿態角與入靶姿態角的差值）均為負值。該實驗采用的鋼筋混凝土靶的等效抗壓強度為46 MPa，混凝土密度約2 500 kg/m3，第1 層靶板厚度為0.30 m，其余各層厚度均為0.18 m。實驗彈體為截卵形彈頭，彈體質量為290 kg，彈體直徑為0.25 m，彈體長徑比為4.8，質心至彈頭長度為0.68 m，轉動慣量JC為35.32 kg·m2，CRH=1.56。本文僅對兩發實驗中無攻角影響的前兩到三層靶體的彈體出靶剩余速度和姿態偏轉角進行了計算，如表2～3 所示，彈體出靶剩余速度的相對誤差均在4%以內，彈體出靶姿態偏轉角的絕對誤差均在0.2°以內，表明本文模型引入的剪切沖塞階段彈體姿態二次偏轉機制是合理的，且能夠準確預測彈體斜侵徹貫穿混凝土薄靶時彈體的出靶剩余速度和姿態偏轉角。

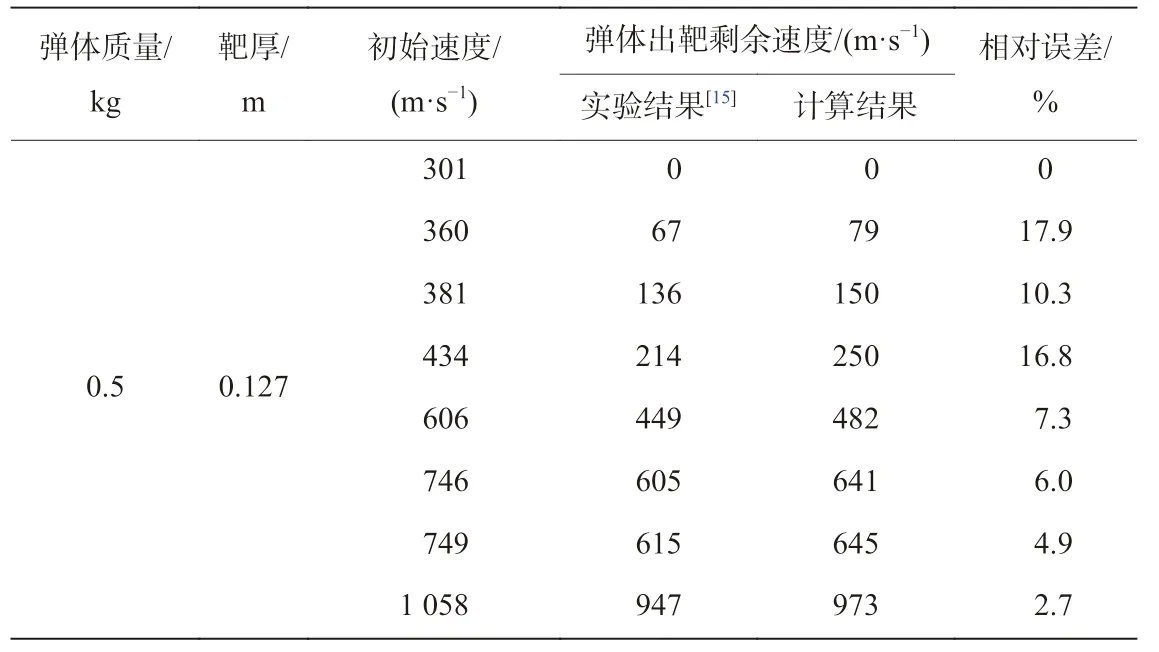
表 1 垂直侵徹普通強度(48 MPa)鋼筋混凝土靶彈體出靶剩余速度的實驗結果與計算結果[15]Table 1 Experimental data and numerical results of the residualvelocities in normal perforation of the normal strength (48 MPa)reinforced concrete targets[15]

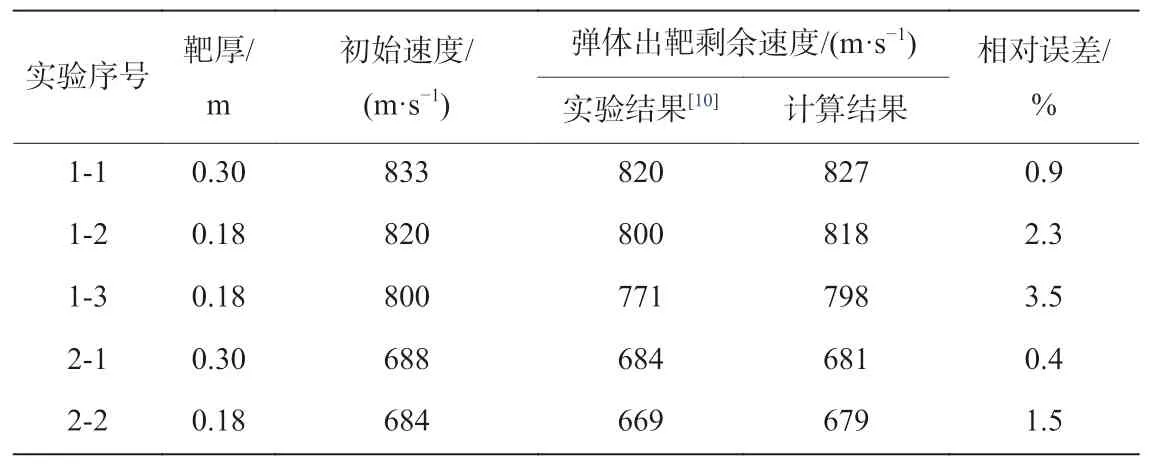
表 2 斜侵徹貫穿多層間隔混凝土薄靶實驗中彈體出靶剩余速度的實驗結果和計算結果Table 2 Experimental data and numerical results of the residual velocities in oblique perforation of the multi-layered thin concrete targets

表 3 斜侵徹貫穿多層間隔混凝土薄靶實驗中彈體出靶姿態偏轉角的實驗結果和計算結果Table 3 Experimental data and numerical results of the attitude deflection angles in oblique perforation of the multi-layered thin concrete targets

4 結 論

（1）在彈體斜侵徹貫穿混凝土靶過程中，考慮了彈體轉動慣量對彈體姿態的影響，并在剪切沖塞階段引入了彈體姿態二次偏轉機制，使彈體姿態在該階段向著姿態角減小的方向偏轉，同時將靶體背面產生的崩落塊形狀修正為對稱錐形圓臺，即令崩落塊中心軸與靶體法線方向重合。計算結果表明本文模型可以準確預測彈體斜侵徹貫穿混凝土薄靶的出靶姿態偏轉角，同時也說明剪切沖塞階段彈體姿態二次偏轉機制的引入和崩落塊形狀的修正是合理的。

（2）通過定義臨界靶厚HL與臨界隧道區長度XL，給出了混凝土靶體厚度的定義區間：當靶厚小于HL時，靶體屬于薄靶；當靶厚大于HL且隧道區長度大于或等于XL時，靶體屬于厚靶；當靶厚大于HL且隧道區長度在0～XL之間時，靶體屬于中厚靶。

（3）剛性彈體斜侵徹貫穿不同厚度混凝土靶時彈體的姿態偏轉由不同機制控制：若靶體為厚靶，則主要由初始開坑階段彈體姿態一次偏轉機制控制；若為薄靶，則由初始開坑階段彈體姿態一次偏轉機制和剪切沖塞階段彈體姿態二次偏轉機制共同控制；若靶體為中厚靶，則由初始開坑階段彈體姿態一次偏轉機制、隧道區的不完整夾持機制以及剪切沖塞階段彈體姿態二次偏轉機制共同控制。