矩形斷面綜合管廊線纜艙通風阻力系數數值仿真研究

陳小峰， 郭 春,*， 鄭 鑫， 張振華

(1. 西南交通大學土木工程學院， 四川 成都 610031；2. 西南交通大學 交通隧道工程教育部重點實驗室， 四川 成都 610031)

0 引言

為優化和完善城市功能品質，加大地下空間綜合開發利用，減少“拉鏈式”馬路的出現，許多城市開始著手規劃、設計、建設城市綜合管廊。為保障這條城市“生命線”的正常運行和日常維護，尤其是保障廊內有毒有害氣體的排出和火災救援[1]，合理的廊內通風必不可少。目前,眾多學者[2-6]對綜合管廊的通風進行了研究，包括通風方式選擇、通風風量計算等。其中，唐志華[5]、李紅雷等[6]基于傳熱學理論，通過計算廊內電纜的載流量和發熱量來研究電纜艙的通風方式、風速、風量的選擇以及通風系統的運行控制方法。另外，周游等[7]采用數值模擬的方法對綜合管廊的電纜艙通風進行研究，分析得到，隨著通風距離的增長，降溫效果減弱，艙內局部溫度過高，需要進行合理的通風分區。

以上研究多集中在廊內通風風量計算、最低風速取值、通風方式選擇以及通風區段優化等方面，而關于綜合管廊通風阻力影響的研究幾乎沒有。由于廊內管線、支架等通風障礙物繁多，它們勢必對通風阻力造成影響。鑒于中國城市綜合管廊的建設起步較晚，目前對管廊通風設計并沒有相關規范，而《城市綜合管廊工程技術規范》[8]中對管廊通風也只是提出最低標準(通風方式、風速、換氣頻率等)，并沒有提及通風阻力系數的取值方法及取值范圍。在全國都在大力建設綜合管廊的背景下，為了使其安全高效地運轉就必須明確其內部通風阻力效應。

本文通過對綜合管廊線纜艙建立1∶1數值模型，利用FLUENT軟件對艙內的通風場景進行模擬，并首次結合流體力學的理論和隧道工程通風阻力系數的研究成果，分析其通風阻力的相關系數。

1 相關理論

雖然關于城市綜合管廊通風阻力效應的研究幾乎為空白，但是在類似構造物(如隧道工程)中通風摩阻研究[9-12]較為成熟。鑒于城市綜合管廊和隧道工程均屬于狹長構造物，部分特性相似，故本研究在流體力學的基礎上借鑒隧道工程通風研究的相關分析方法，得到以下計算公式。

在城市綜合管廊中，風流的沿程阻力(摩擦阻力)表達式為：

(1)

式中：hf為管廊通風的沿程阻力，Pa；λ為沿程阻力系數；L為管廊長度，m；d為管廊截面當量直徑，m；ρ為管廊內空氣密度，kg/m3；v為管廊內平均風速，m/s。

由于支架對空氣流動的影響屬于局部阻力，故管廊通風的局部阻力

(2)

式中ξ為局部阻力系數。

因此，城市綜合管廊線廊艙的通風阻力h為沿程阻力和局部阻力之和，即：

(3)

若斷面為非圓形的不規則形狀，管廊截面當量直徑

(4)

式中：A為廊內空氣過流斷面面積，m2；U為廊內空氣過流斷面周長，m。

在工程上，局部阻力系數只與阻礙物幾何形狀有關[13]。在實際綜合管廊工程中，支架在縱向上為均勻排列，且形狀一致，故每處支架產生的局部阻力相同。為簡化計算，可以將管廊劃分成若干相等的區段，且每段只含1個豎排支架，則整個管廊的通風阻力可表示為：

(5)

式中：λi為第i個管廊區段的沿程阻力系數；l為管廊區段長度，m；vi為第i個管廊區段的平均風速，m/s。

當廊內通風量一定時，如果過流斷面相同，根據Ai·vi=Aj·vj近似有vi=v，則各區段雷諾數Re近似相同。在紊流中，沿程阻力系數可表示為：

(6)

式中k為管廊內壁絕對粗糙度，m。

鑒于k和d分別為定值，故各管廊區段的λ值也可近似認為相等，則式(5)可以轉化為：

(7)

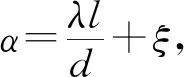
(8)

為方便求得通風阻力h，所取管廊線纜艙模型假設沒有縱坡，依據仇玉良等[14]的研究結果，其進出口間的通風阻力

(9)

式中：p1、p2分別為管廊進、出口斷面靜壓，Pa；v1、v2分別為管廊進、出口斷面風速，m/s。

2 數值模擬

2.1 模型概況

根據《城市綜合管廊工程技術規范》[8]中的相關規定，綜合管廊標準斷面內部凈高應根據容納管線的種類、規格、數量、安裝要求等綜合確定，不應小于2.4 m； 管廊內部兩側設置支架或管道時，檢修通道凈寬不得小于1.0 m。結合《電力工程電纜設計規范》[15]中對于支架間距的規定，建立斷面為2.5 m×3.0 m的矩形管廊線纜艙模型，其縱向長度為20 m。為模擬支架和線纜對線纜艙內部通風的影響，在該模型中建立支架和線纜模型，具體情況為：支架為0.75 m×0.05 m× 0.05 m(長×寬×高)的長方體，附著于綜合管廊線纜艙的兩側壁，縱向間距為1 m，橫斷面上間距為0.25 m；線纜為長直圓柱體，半徑為0.04 m，長度為20 m，在每一層支架上均勻布置3根線纜，共計11層，左右兩側均勻布置。綜合管廊線纜艙幾何模型如圖1所示。

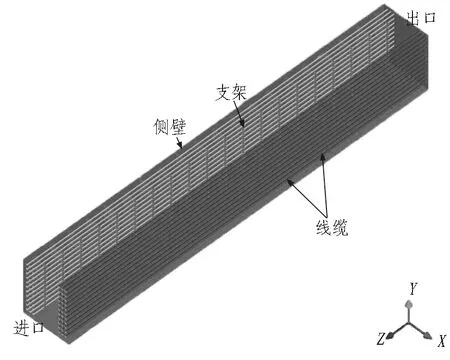
圖1 綜合管廊線纜艙幾何模型

本模型中流體采用ANSYS ICEM CFD軟件建模并劃分結構化網格，管廊內壁面(包含支架、管線表面)采用標準壁面函數法進行處理，并滿足文獻[16]中的精度要求。數值模型有6 189 550個六面體單元，并且精度較高(最小Quality值為0.5)。綜合管廊線纜艙網格劃分情況如圖2所示。

圖2 綜合管廊線纜艙部分網格情況

另外，為了更方便地描述綜合管廊線纜艙內部線纜和支架等對通風阻力的影響，根據線纜艙橫斷面和線纜、支架迎風面幾何形狀特點，可得到“通風障礙物比例”，即綜合管廊線纜艙橫斷面中支架和線纜的迎風面積占該橫斷面總面積的比例。本模型的橫斷面通風障礙物比例值約為15%。

2.2 計算參數及模型選用

本模型采用ANSYS FLUENT軟件進行模擬，主要模擬2種情況： 不考慮熱效應和考慮熱效應對通風的影響。

2.2.1 不考慮熱效應對通風的影響

在這種情況下只考慮不同通風風速對通風阻力的影響。值得注意的是，本研究中數值模型模擬實際管廊中的一段，定義的風速為斷面平均風速。依據《世博會園區綜合管溝建設標準》[17]，廊內風速不宜大于1.5 m/s，且出風口風速不得大于5 m/s，故本文中斷面風速取值為0.3～3.0 m/s(間隔0.3 m/s)。

對通風阻力系數進行研究時，相關參數取值如下： 空氣為理想的不可壓縮氣體，空氣密度ρ=1.225 kg/m3；環境大氣壓p=10 325 Pa；運動黏滯系數μ=1.52×10-5kg/(m·s)。

2.2.2 考慮熱效應對通風的影響

熱效應主要由線纜發熱和進風溫度所引起。

1)模擬線纜發熱對通風的影響時，主要分2個方面： 線纜發熱一定，不同通風風速下的通風模擬； 通風風速一定，不同線纜發熱量下的通風模擬。

線纜產生的熱量在通過線纜外表面時的熱流密度q恒定[18]，故可采用第2類熱邊界條件。新鮮空氣從進口流入時，進風溫度恒定為T=303.16 K，艙內溫度恒定為T=303.16 K。

2)模擬進風溫度對通風的影響時，線纜發熱量視為恒定(熱流密度q=18 W/m2)，進風風速也視為恒定(1.5 m/s)，然后改變進風溫度(278.16～303.16 K)。

另外，在考慮熱效應對通風的影響時，由于流體計算域內的空氣溫差較小，空氣采用Boussinesq近似模型(空氣密度ρ=1.225 kg/m3)來模擬空氣在熱效應作用下的升浮力。艙室的頂部、底部以及兩側的混凝土壁視為絕熱壁，即熱流密度為0。

2.2.3 計算模型及其他參數設置

鑒于綜合管廊各艙室中風速一般不是很大，且本文主要研究內容是線纜艙通風阻力效應，其計算的湍流模型為標準雙方程模型。

模擬過程中，利用分離式求解器穩態計算模式，采用SIMPLE計算方法。

為模擬線纜艙內部各類壁面粗糙度對通風摩擦阻力的影響，根據現行《公路隧道通風設計細則》[19]附錄中對混凝土壁粗糙高度的規定取Δ=0.5 mm；另外，根據相關文獻中對支架表面的粗糙高度的研究，支架表面粗糙高度取Δ=0.1 mm[20]；鑒于線纜艙中線纜由高分子復合材料制成，表面光滑，故其粗糙高度取0。

數值模擬各邊界條件如表1所示。

表1綜合管廊線纜艙數值模擬邊界條件

Table 1 Numerical simulation boundary conditions of utility tunnel cable cabin

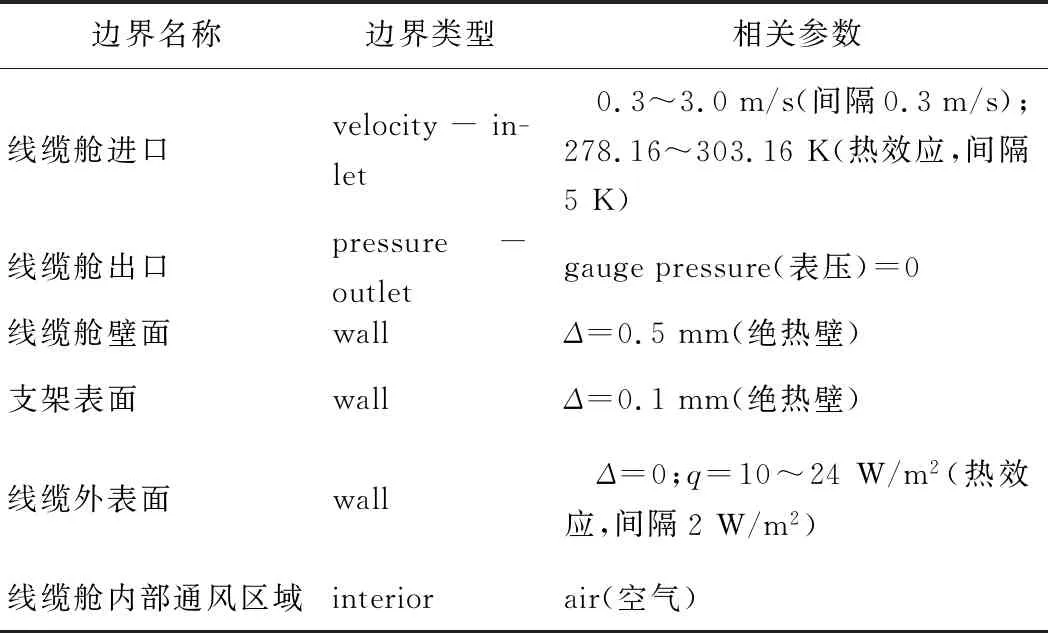
邊界名稱邊界類型相關參數線纜艙進口velocity-in-let 0.3～3.0m/s(間隔0.3m/s);278.16～303.16K(熱效應,間隔5K)線纜艙出口pressure-outletgaugepressure(表壓)=0線纜艙壁面wallΔ=0.5mm(絕熱壁)支架表面wallΔ=0.1mm(絕熱壁)線纜外表面wall Δ=0;q=10～24W/m2(熱效應,間隔2W/m2)線纜艙內部通風區域interiorair(空氣)

2.3 模擬結果

根據管廊縱向幾何尺寸，本數值模擬過程中以1 m的管廊長度(含1個豎排支架)為單位長度進行計算。

根據模擬結果，取進口斷面和出口斷面的靜壓差、動壓差之和，即可得到總的通風阻力，再根據式(8)可求出綜合管廊單位長度的通風阻力系數。

在不考慮熱效應的前提下，綜合管廊線纜艙內有、無支架和線纜對通風的影響如表2所示。表2中差異值為綜合管廊線纜艙有支架和線纜時對應參數與沒有支架和線纜時的比值。

改變通風風速，并考慮線纜艙內支架、線纜及壁面粗糙程度，有線纜熱效應(熱流量q=18 W/m2)和無熱效應(熱流量q=0)2種情況下對艙內通風影響的對比分析如圖3所示。

通風風速恒定(1.5 m/s)，艙內溫度恒定(303.16 K)以及進風溫度固定(303.16 K)的情況下，線纜不同熱流量對艙內通風的影響如圖4所示。

通風風速恒定(1.5 m/s)，艙內溫度恒定(303.16 K)以及線纜發熱量固定(熱流量q=18 W/m2)的情況下，進風溫度對艙內通風的影響如圖5所示。

進風溫度恒定(303.16 K)，艙內溫度恒定(303.16 K)以及線纜發熱量固定(熱流量q=18 W/m2)的情況下，通風風速變化時的溫度場如圖6—8所示。

表2綜合管廊線纜艙有、無支架和線纜情況下通風阻力情況對比

Table 2 Comparison of ventilation resistance of utility tunnel cable cabin with and without brackets and cables

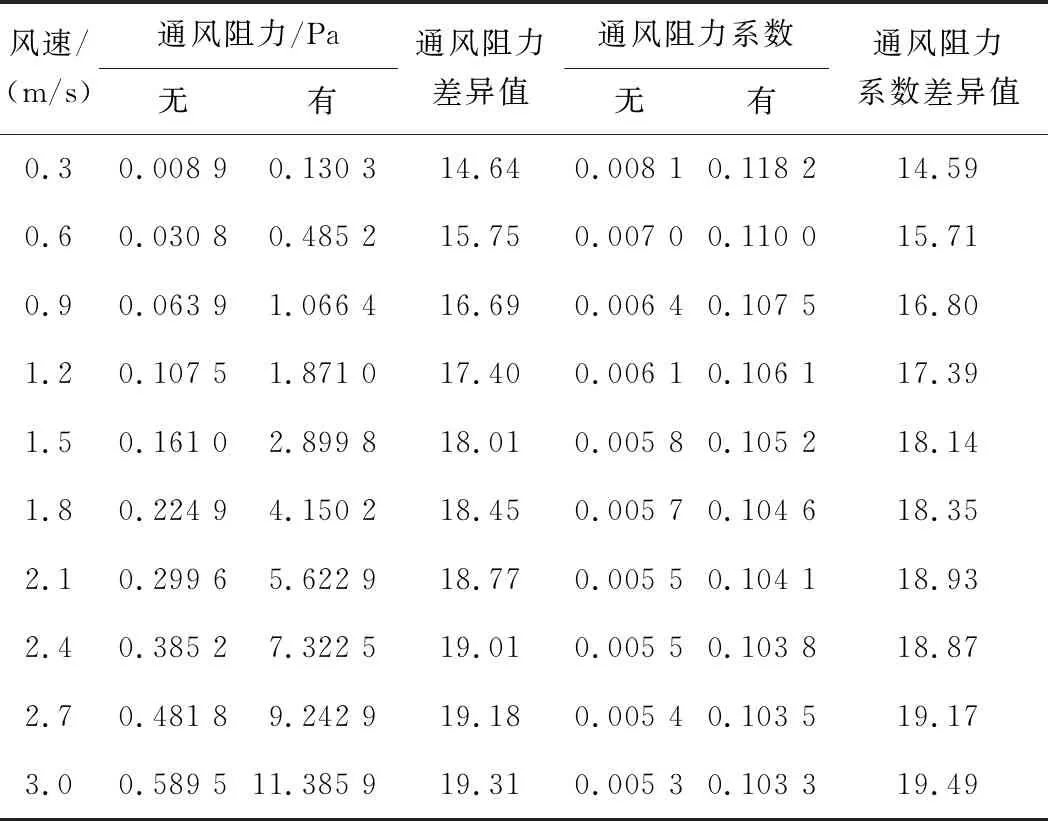
風速/(m/s)通風阻力/Pa無有通風阻力差異值通風阻力系數無有通風阻力系數差異值0.30.00890.130314.640.00810.118214.590.60.03080.485215.750.00700.110015.710.90.06391.066416.690.00640.107516.801.20.10751.871017.400.00610.106117.391.50.16102.899818.010.00580.105218.141.80.22494.150218.450.00570.104618.352.10.29965.622918.770.00550.104118.932.40.38527.322519.010.00550.103818.872.70.48189.242919.180.00540.103519.173.00.589511.385919.310.00530.103319.49

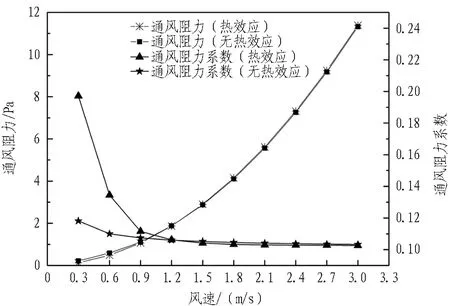
圖3 線纜有、無熱效應通風情況對比

Fig. 3 Comparison of ventilation situation under conditions of cables with and without thermal effect

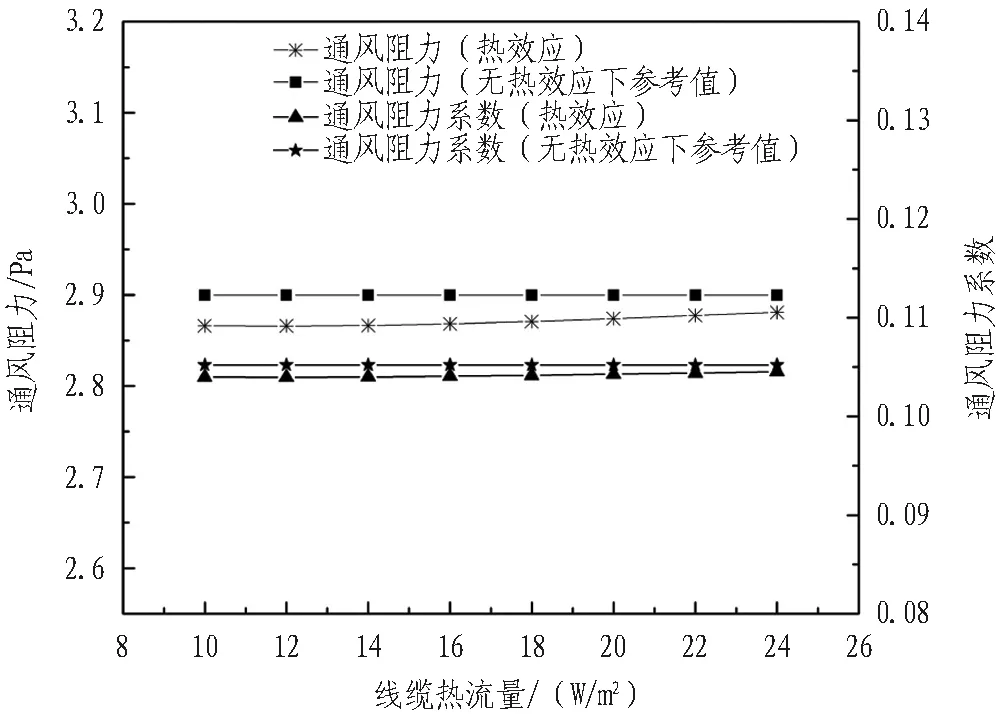
圖4不同線纜熱流量下通風情況對比

Fig. 4 Comparison of ventilation situation under conditions of different cable heat fluxes

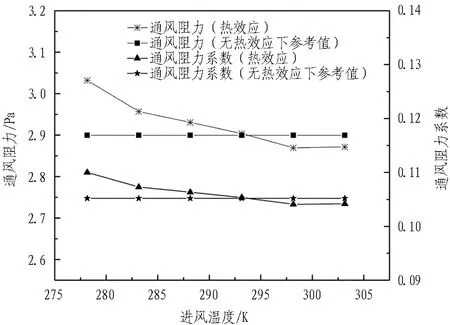
圖5 不同進風溫度下通風情況對比

Fig. 5 Comparison of ventilation situation under conditions of different inlet air temperatures

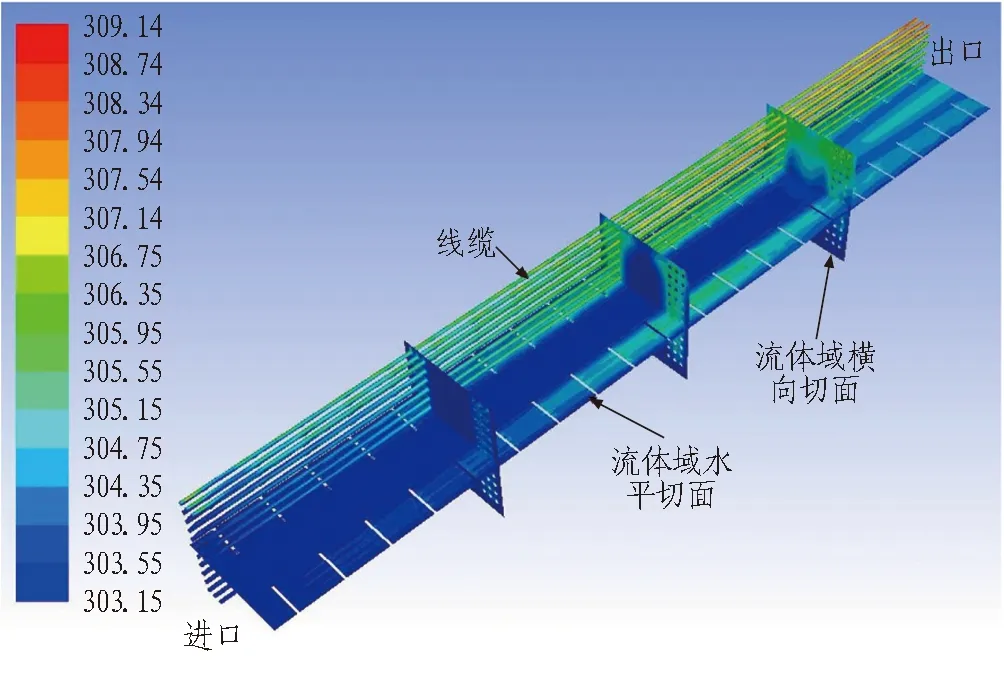
圖6 進口風速0.6 m/s下考慮熱效應的溫度場(單位： K)

Fig. 6 Temperature field considering thermal effect at an inlet air speed of 0.6 m/s (unit: K)

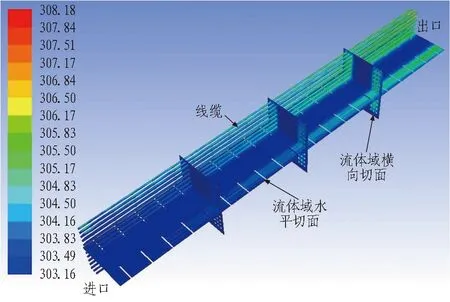
圖7 進口風速1.2 m/s下考慮熱效應的溫度場(單位： K)

Fig. 7 Temperature field considering thermal effect at an inlet air speed of 1.2 m/s (unit: K)

3 結果分析

3.1 無熱效應的情況

在沒有考慮熱效應的情況下，不同通風風速，有支架、線纜的管廊通風阻力和通風阻力系數是沒有時的14～20倍(見表2)。由此可見，城市綜合管廊線纜艙內部支架、線纜等對其通風阻力有極大的影響，在通風設計時需著重考慮。

圖8 進口風速1.8 m/s下考慮熱效應的溫度場(單位： K)

Fig. 8 Temperature field considering thermal effect at an inlet air speed of 1.8 m/s (unit: K)

由表2和圖3可以得到： 隨著斷面風速的增大，含支架、線纜的線纜艙內部通風阻力逐漸增大，并且增長速率越來越大。這是因為在充分發展的紊流中，通風阻力與風速的平方成正比。

另外，本模型中所有工況均為紊流，沿程阻力系數隨Re增大而逐漸減小(見式(6))；局部阻力系數只與阻礙物幾何形狀有關； 因此，隨著斷面風速的增大，線纜艙內通風阻力系數逐漸減小，并趨于平穩(見圖3)。

3.2 有熱效應的情況

隨著空氣溫度增加，空氣分子熱運動加劇，由碰撞和摩擦導致的機械能損失增大。圖3中風速為0.3～0.6 m/s時，進口斷面風速過小，對艙內的散熱效果不好，空氣被加熱(如圖6所示)而導致通風阻力較大，因而該情況下的通風阻力系數較大。而風速大于0.9 m/s時，廊內通風散熱情況較好，空氣溫度較低，故通風阻力系數總體變化不大。

根據圖4中結果，在斷面風速一致(1.5 m/s)的情況下，與無熱效應的情況相比，艙內線纜發熱量導致通風阻力和通風阻力系數均減小，但是整體差異不大。由圖5可以看出，當其他條件固定時，進風溫度對艙內通風有一定的影響，其通風阻力和通風阻力系數隨著進風溫度的增加而逐漸減小。出現這一現象的原因在于“煙囪效應”，即在沒有機械通風動力的情況下(進口斷面風速為0)，由于進口斷面溫度較低，廊內上部氣流由于密度差會向進口段面流動(如圖9所示)，故而導致通風阻力增大； 但是，隨著進口斷面溫度逐漸升高，溫度差逐漸降低，由溫差引起的阻力逐漸減小。

另外，依據圖6—8的結果可以得到，其他條件固定的情況下，隨著斷面風速的增加，艙內的最高溫度逐漸降低，并且線纜發熱對艙內空氣的溫度影響較小，其最大影響范圍在出口斷面附近的線纜周圍，對艙內過道的空氣溫度幾乎沒有影響。

圖中所取平面為X=0.8 m的Y-Z平面(本模型X、Y、Z方向取值范圍分別為0～2.5 m、0～3.0 m和-20～0 m)。

圖9進口斷面風速為0、溫度為278.16K時氣流縱向流速方向

Fig. 9 Longitudinal speed direction at an inlet air speed of 0 and temperature of 278.16 K

4 結論與討論

本文通過ANSYS FLUENT軟件模擬分析了城市綜合管廊線纜艙的支架、線纜和相關熱效應對通風風流的影響，并得到綜合管廊線纜艙通風阻力效應的相關結論：

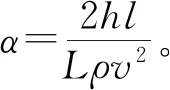
2)針對同一綜合管廊線纜艙，隨著進口風速的增加，線纜艙內的通風阻力逐漸增大，而通風阻力系數逐漸變小，并且趨于穩定。

3)進口空氣溫度、線纜發熱及艙內溫度產生的熱效應對艙內通風的阻力效應有一定的影響，并且隨著進風溫度增大，通風阻力和通風阻力系數逐漸降低。

4)本模型的橫斷面通風障礙物比例值約為15%，而綜合管廊通風系統設計中斷面風速一般不宜大于1.5 m/s。根據本研究結果，當通風障礙物比例值約為15%，且斷面風速取1.5 m/s時可取通風阻力系數約為0.105 2。

結合實際綜合管廊工程，本模擬結果還有一些不足之處，如管廊縱坡和管廊交叉部位等細節未納入模擬等。下一步，筆者所在課題組將進行模型試驗和工程實測來修正相關結論，以期提出適用于實際工程的通風阻力參數。