基于改進混沌理論的網絡輿情短期預測策略方法研究
高 穎
(1.南開大學 周恩來政府管理學院, 天津 300000;2.內蒙古民族大學 人事處, 內蒙古 通遼 028000)
輿情是一定時期、一定范圍內民眾對社會現實的主觀反映,是群體性的思想、心理、情緒、意見和要求的綜合表現[1]。隨著互聯網的迅速發展和智能手機的廣泛使用,網絡已成為一種主導性的信息傳播方式。國內外的重大事件都可能在互聯網上快速傳播,引發社會公眾的廣泛關注和討論,從而造成極大的輿論壓力,成為任何國家和部門都必須面對的社會問題。
從一定程度上看,互聯網已成為新時代社會輿論的放大器。一方面,網絡能夠起到社會監督的作用;但另一方面,如果引導和監管不善,負面輿情可能對公共安全造成威脅。網絡輿情具有突發性、隱蔽性和多元化等特點,因此相關部門對網絡輿情的處理可能滯后。加強對網絡輿情的監控和疏導,提前預測輿情發展趨勢,盡最大可能化解矛盾,對維護社會穩定、保障國家安全具有重大意義[2]。
從當前研究看,輿情預測的方法總體可分為兩類:一類是傳統的時間序列預測方法,如指數平滑法[3]、灰色預測法等[4-5];另一類是現代智能機器學習方法,如小波理論[6]、神經網絡及其改進方法等[7-9]。指數平滑法適合時間序列平穩情況的預測。灰色預測法適用于具有指數變化趨勢的原始樣本,對隨機波動較大的樣本效果不佳。神經網絡能夠逼近復雜的非線性關系,但是存在網絡結構難以確定、過擬合等問題。
最小二乘支持向量機(least squares support vector machine,LS-SVM)是近年發展起來的一種機器學習方法,能夠避免標準SVM訓練時間長,神經網絡存在的過擬合等問題,具有較強的泛化能力[10-11]。在LS-SVM建模中,傳統的訓練樣本和模型參數選取依靠預測者自身經驗,導致訓練時間長,并且一旦選定訓練樣本就只能通過模型參數優化來反復修正模型,直到達到滿意的訓練效果。粒子群算法[12-13](particle swarm optimization,PSO)是由J.Kennedy和R.C.Eberhart等提出的一種進化算法,具有計算過程簡單、優化精度高、收斂速度快等優點,適用于對LS-SVM參數進行優化。本文在混沌理論相空間重構的基礎上,用LS-SVM擬合網絡輿情相空間中相點的演化趨勢,通過PSO算法尋找最優LS-SVM參數,最后以“8·25”事件為案例進行仿真實驗,對模型進行驗證。
1 相關理論
1.1 相空間重構理論
相空間重構(phase space reconstruction,PSR)是根據有限的數據在重構的相空間中把混沌吸引子恢復出來以研究系統動力學特性的方法。在進行相空間重構時,通常只考慮一個變量,然后將該變量在固定時間延遲點上的測量作為一個新維,進而確定多維狀態空間中的一個點。通過重復上述過程,就可用一個分量重構出原動力系統模型。
對于混沌時間序列{xi,i=1,2,…,n},n為樣本個數。根據Takens定理,重構相空間為:
(xi,xi+τ,…,xi+(m-1)τ),i=1,2,…,M
(1)
式中:xi表示相空間的點;m表示嵌入維數;τ為延遲時間;M為重構相空間中相點個數,M=n-(m-1)τ。重構相空間的吸引子矩陣為:
(2)
相空間重構結果的好壞取決于m和τ。目前,確定m和τ的方法主要包括兩種思路:一種是兩者獨立確定;另一種是聯合確定。依據Takens定理,對于無限長、無噪聲的時間序列,τ可以是任意值。但事實上真實時間序列往往都有噪聲,同時不能保證時間序列的長度足夠長。C-C法[14]基于嵌入窗的思想,在確定τ的過程中同時得到合適的m,并且該方法計算量小、具有較強的抗噪聲能力,因此采用C-C法進行相空間重構。
1.2 LS-SVM
給定一組訓練樣本D={(xk,yk)|k=1,2,…,N},xk∈Rn,yk∈R。xk為輸入向量,yk為輸出向量,n為訓練樣本數。
最小二乘支持向量機回歸模型可表示如下:
y=wTφ(x)+b
(3)
式中:φ(·)為映射函數;w為特征空間的權向量;b為偏置量。
根據結構風險最小化原則,LS-SVM函數估計問題可描述為:
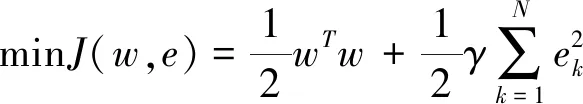
(4)
式中:γ為誤差懲罰參數;ek為誤差變量,ek∈R。
滿足以下約束:
yk=wTφ(xk)+b+ek
(5)
通過構建非線性映射函數,能夠提取原始空間的特征,因此原始的線性不可分問題得到解決。定義拉格朗日函數如下:
L(w,b,e;α)=J(w,e)-
(6)
式中:αk為拉格朗日乘子,αk∈R。
根據KKT條件,對式(6)進行優化,即:
(7)
消去特征空間的權向量w和e,得到矩陣方程如下:
(8)
其中:
e=[e1,e2,…,eN],lv=[1,1,…,1]
y=[y1,y2,…,yN],α=[α1,α2,…,αN]
Ωkl=φT(xk)φ(xl),l=1,2,…,N)
根據Mercer條件,存在映射φ和核函數K(·,·)使:
K(xk,xl)=φT(xk)φ(xl)
(9)
由式(8)和式(9)聯立求出α和b后,得到最小二乘支持向量機回歸算法的函數估計式為:
(10)
式(10)取不同的核函數生成不同的支持向量。徑向基核函數(RBF)在時間序列預測中取得了較好的效果,本文選取RBF核函數為LS-SVM的核函數。確定核函數以后,需要尋找最優的核函數參數σ和誤差懲罰參數γ。
1.3 PSO算法
粒子群算法是基于鳥類個體之間的協作和信息共享尋找最優解,非常適用于連續域優化問題的解決。粒子群算法初始化為一組隨機粒子,然后通過不斷迭代尋找最優解,各粒子的優劣度用適應度函數表示。種群中每個粒子表示一個可能的解向量,通過跟蹤個體極值和全局極值實時更新位置和速度,實現最優目標。設粒子的位置和速度分別是Xi和Vi,則其更新策略為:
(11)
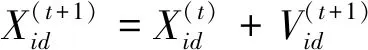
(12)
(13)
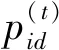
為了減少依靠主觀經驗選取參數的盲目性和工作量,提高訓練效果,本文采用粒子群算法選取LS-SVM的最優參數σ和γ,基本流程如圖1所示。
步驟1初始化粒子的初始位置和速度等。
步驟2用初始粒子對最小二乘支持向量機訓練樣本進行學習,從而獲得當前位置的訓練誤差,將其作為粒子適應度值。對比粒子的當前適應度值和最優適應度值,若結果更優,則當前位置即為該粒子的最優位置。
步驟3計算慣性權重,并用式(11)和式(12)更新粒子的速度和位置。
步驟4計算適應度值,判斷是否符合尋優終止條件(最大迭代次數或設定的精度要求),如果滿足則得到最優解,否則轉至步驟3。
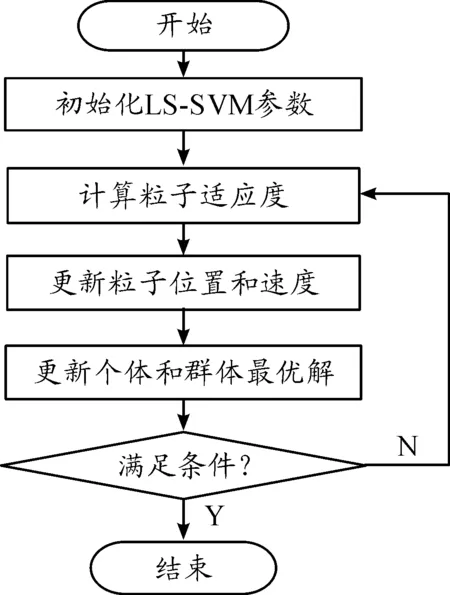
圖1 PSO算法優化LS-SVM參數的基本流程
2 混沌理論和LS-SVM結合的網絡輿情預測模型
2.1 數據預處理
網絡輿情具有非線性、隨機性的特點,原始數據之間相差比較大。因此,在將數據輸入到LS-SVM訓練之前,將原始樣本進行歸一化處理:
(14)
式中:xi表示原始樣本;ximin、ximax分別為原始樣本的最小值和最大值。
然后,對網絡輿情的預測結果進行反歸一化,即:
(15)
2.2 LS-SVM預測器的輸入輸出結構
混沌相空間中,任一相點xi演變到下一相點xi+1可用函數表示如下:
f:xi+1=f(xi)
(16)

2.3 預測步驟
基于改進混沌理論的網絡輿情短期預測步驟如下:
步驟1對輿情原始數據進行預處理;
步驟2相空間重構。用C-C法確定最佳延遲時間τ和嵌入維數m,建立網絡輿情時間序列的多維相空間;
步驟3構造輸入輸出向量,形成訓練樣本和預測樣本;
步驟4用PSO算法對LS-SVM參數進行優化,尋找最優的參數σ和γ;
步驟5在上述基礎上,代入預測樣本用已訓練好的學習機器進行預測,獲得網絡輿情的預測值。
2.4 預測精度評價
當前用于表征預測結果精度的指標主要有:平均絕對值相對誤差(MAPE)、相對誤差(RE)和均方根誤差(RMSE)等。本文采用MAPE作為預測結果精度評價指標:
(17)
3 仿真實驗
3.1 數據來源與預處理
為驗證所建輿情預測模型的有效性,對2018年哈市發生的“8.25”火災事件進行預測分析。通過對百度新聞、搜狐網、騰訊網、今日頭條等網站進行跟蹤調查統計,得到“8.25”事件發展過程中的點擊量、評價量和轉載量,用式(14)對網絡輿情歷史數據進行歸一化處理。由于篇幅限制,僅以事件發生后10天內的點擊量預測為案例進行仿真,如表1所示。
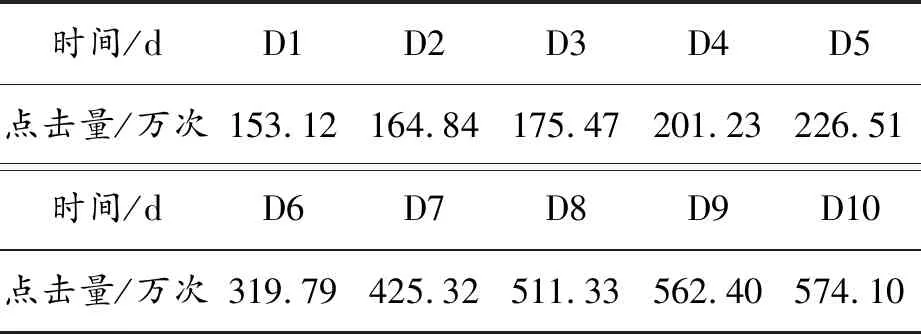
表1 “8.25”事件點擊量
3.2 模型的訓練結果與分析
3.2.1相空間重構
基于混沌理論進行相空間重構,用C-C法確定最優延遲時間τ=1,最優嵌入維數m=4。相空間重構后得到6組樣本集,屬于典型的小樣本預測問題。用前4組樣本作為訓練樣本,用于訓練支持向量機模型,后兩組樣本作為預測樣本,用于檢驗模型的預測能力。
3.2.2LS-SVM參數尋優
用LS-SVM對重構的網絡輿情預測樣本進行訓練,構建訓練樣本的適應度函數如下:
(18)
粒子群算法基本參數設置為:種群數N為20,學習因子c1為1.5,c2為1.5,慣性權重ω為0.5,最大迭代次數Gmax為80。在Matlab2014下進行仿真,得到最優的誤差懲罰參數γ=744,最優的寬度參數σ2=0.51。粒子群算法的參數尋優過程如圖2所示。
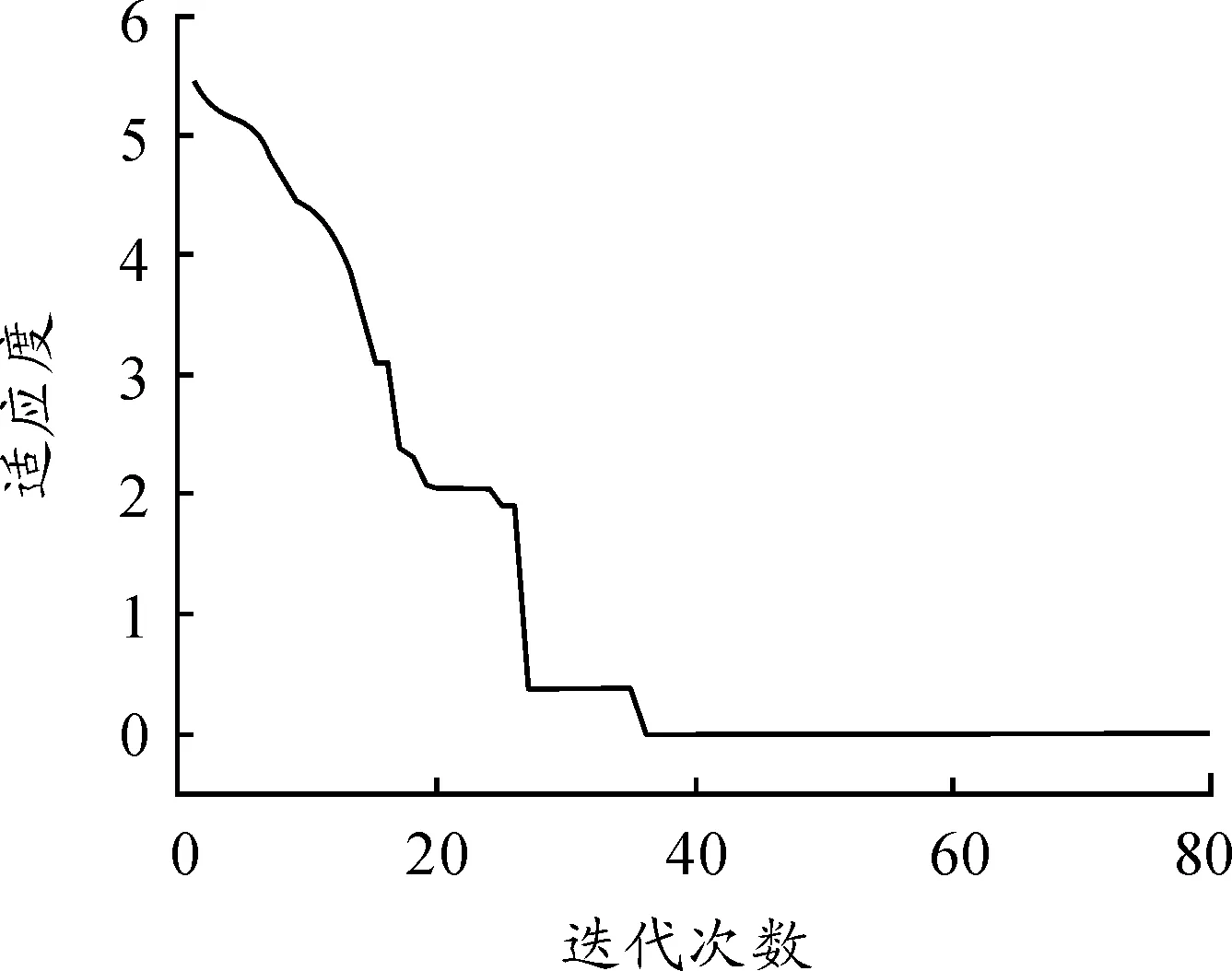
圖2 PSO參數進化過程
3.2.3模型訓練和分析
對網絡輿情訓練樣本進行訓練,結果如圖3所示。可以看出網絡輿情訓練樣本的真實值和輸出值基本上重合,說明所建模型訓練精度較高。

圖3 模型訓練結果
3.3 模型的預測結果與分析
在建立上述學習機器的基礎上,對網絡輿情第9天和第10天的點擊量進行預測,并與未進行PSO參數優化的預測結果對比,結果見表2。
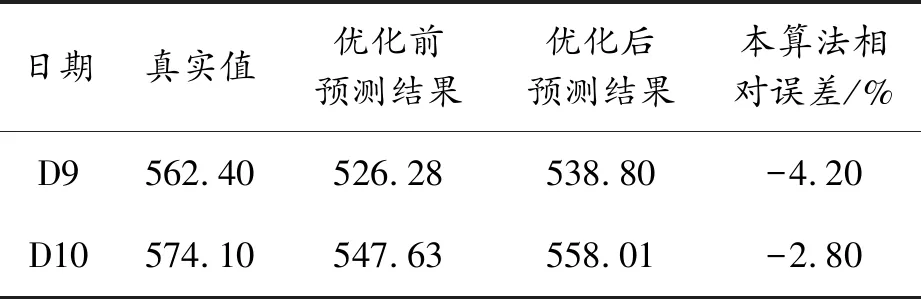
表2 網絡輿情的預測結果
從表2可以看出:參數經過優化后的預測結果更加接近真實值,第9天、第10天的預測結果相對誤差絕對值均小于5%。計算得MAPE=3.50%,說明基于改進混沌理論和LS-SVM的預測模型對網絡輿情短期預測能夠取得較好的預測效果,具有廣泛的應用前景。
4 結論
1) 針對網絡輿情數據隨機波動大、小樣本的特點,通過引入混沌理論對網絡輿情時間序列進行相空間重構,用C-C法確定最佳嵌入維數和延遲時間,避免了依靠預測者主觀經驗的盲目性。
2) PSO算法用于LS-SVM參數尋優具有計算簡單、運算速度快的特點,能夠尋找到最佳的LS-SVM參數,避免了主觀選擇參數的盲目性,提高了建模精度。
3) 通過對網絡輿情第9天、第10天的預測結果分析,MAPE值為3.50%,并且每天的預測值相對誤差絕對值都小于5%,說明本文所提方法具有較高的預測精度和廣泛的應用前景。

