應用于軟件缺陷預測模型的量子粒子群優化BP算法

洪曉彬，姜利群，趙 鵬

(1.廣州工商學院 計算機科學與工程系, 廣州 510850；2.中國礦業大學 計算機學院, 江蘇 徐州 221116;3.太原師范學院 計算機科學與技術系, 太原 030619)

從20世紀90年代開始，隨著計算機的普及和推廣，電腦操作系統得到了快速發展。各類軟件應用程序也迅速出現并在越來越多的企業中得到應用。企業需求的不斷增多和技術的不斷進步，導致軟件的復雜度呈現出指數型增長態勢[1]，其功能和存儲大小都不斷增加。越來越復雜和龐大的軟件程序使出現故障的可能性也隨之不斷提高，而現在的企業已十分依賴軟件系統。如果軟件程序出現故障，會對企業造成不可預知的嚴重影響。因此，軟件的缺陷分析成為了軟件開發步驟中必要的環節。通過軟件缺陷分析，能夠有效地確保軟件質量，加強軟件的安全性。

目前，通常將軟件失效分為3個方面：軟件錯誤(software error)、軟件故障(software fault)、軟件缺陷(software defect)。其中，軟件缺陷是指系統或系統部件中那些導致系統或部件不能實現其功能的缺陷。軟件缺陷屬性包括缺陷標識、缺陷類型、缺陷嚴重程度、缺陷產生可能性、缺陷優先級、缺陷狀態、缺陷起源、缺陷來源、缺陷原因。在軟件開發的過程中，軟件缺陷的產生是不可避免的。因此，如何準確、有效地發現，并快速修復軟件缺陷成為研究的一個熱點。文獻[4]提出了一種評估動態系統中軟件構件可靠性的模型選擇方法；文獻[5]提出一種基于優化BP神經網路的軟件缺陷預測方法，通過灰狼優化算法克服BP神經網絡陷入局部搜索，從而解決其參數設置依賴性問題；文獻[6]運用粒子群優化算法(PSO)優化BP神經網絡的權值和閾值，提出了一種基于PSO-BP軟件缺陷預測模型，在一定程度上提高了預測的準確性。

相比PSO算法，量子粒子群優化算法通過結合量子進化理論，進一步提升了全局搜索能力，能在一定程度上克服BP神經網絡算法在收斂性能上的不足。因此，本文將量子粒子群算法和BP神經網絡相結合，以提高軟件缺陷預測模型的準確性和適用性。以3層BP神經網絡構為基礎，運用量子粒子群優化算法對BP神經網絡的權值和閾值進行優化，從而在調節參數較少的條件下優化全局搜索能力。仿真實驗結果顯示：相比傳統BP神經網絡和粒子群優化BP神經網絡，提出的軟件缺陷預測模型算法在準確率、效率方面均得到有效提高。

1 相關工作

軟件缺陷預測模型可以有效節約軟件測試項目的成本和資源，提高軟件工程質量。近幾年，基于BP神經網絡的軟件缺陷預測技術研究成為了主流。

1.1 BP神經網絡架構

BP神經網絡的本質是一種多層次的前饋網絡，典型的架構為3層感知模型[7-8]。3層BP神經網絡模型結構包含1個輸入層、1個隱含層和1個輸出層，如圖1所示。

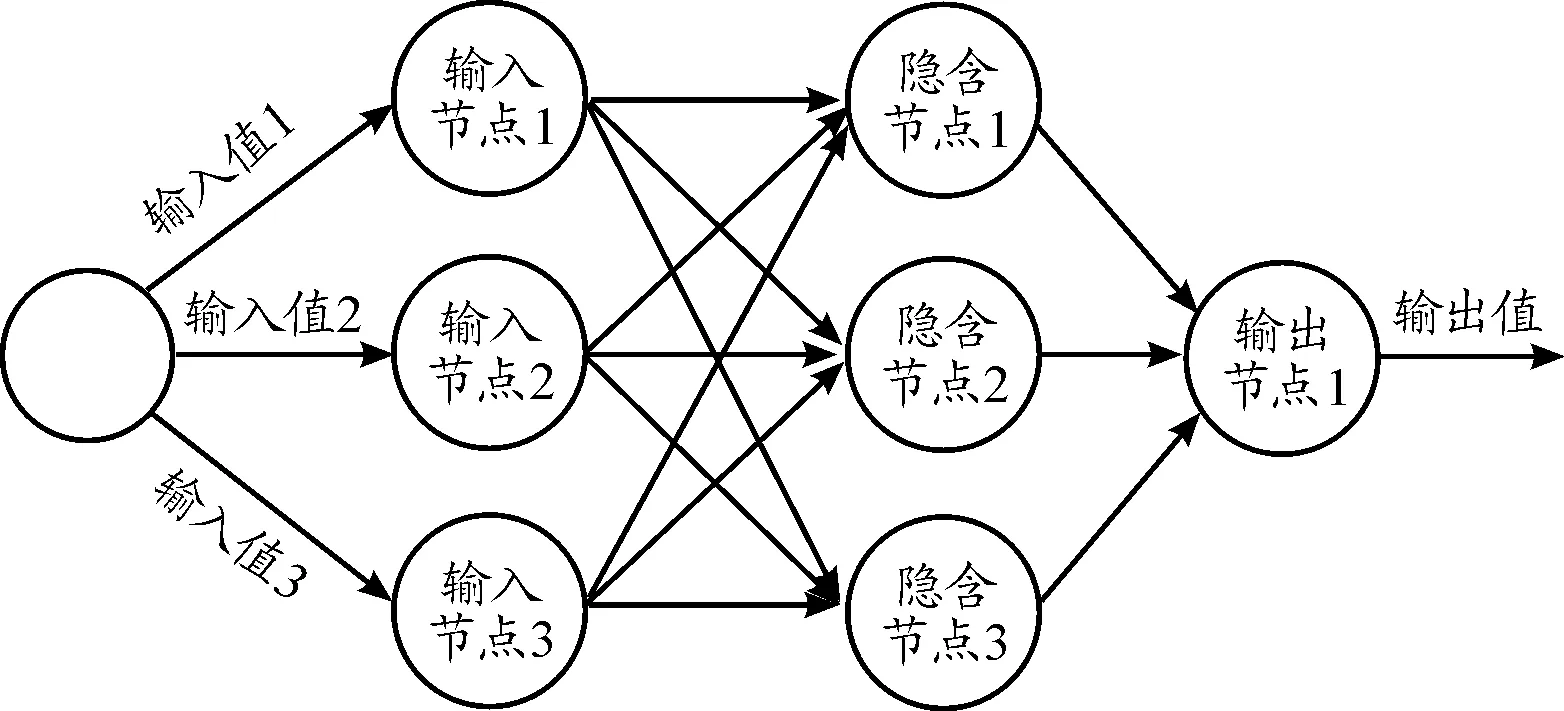
圖1 3層BP神經網絡模型結構

在第1層(輸入層)中輸入和輸出分別為：

(1)

(2)

在第2層(隱含層)中，利用高斯函數對上一層的數值進行分類。該層的輸入和輸出分別為：

i=1,2;j=1,2,…,n

(3)

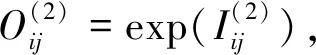
i=1,2;j=1,2,…,n

(4)

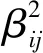
輸出層的輸入和輸出分別為：

(5)

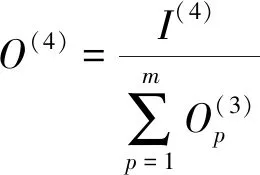
(6)

其中W為連接權重。

參數αij和參數βij的更新方法如下：

λ(αik(t)-αik(t-1))

(7)

λ(βik(t)-βik(t-1))

(8)

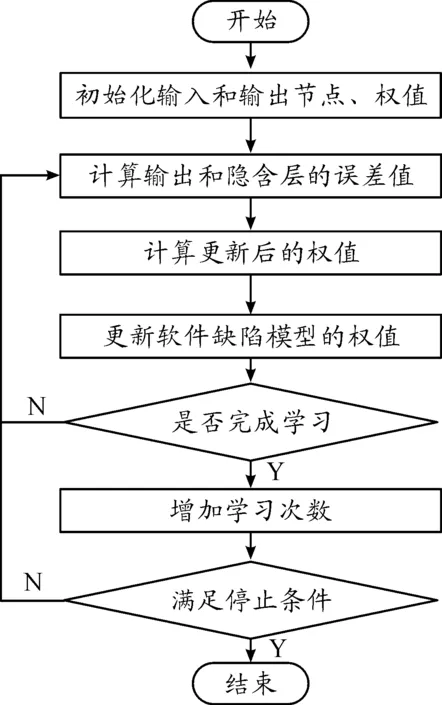
圖2 基于BP神經網絡的軟件缺陷預測流程

1.2 量子粒子群優化算法

群智能優化算法作為一種人工模仿動物群體生活習性的仿生技術，在數據挖掘算法方面具有較大的應用前景。例如，粒子群優化算法作為群智優化的重要方法之一，能夠模擬簡單群落中個體以及個體之間的互動行為來搜索全局最優解[9]。2004年提出的量子粒子群優化算法通過結合量子進化理論，進一步提升了全局搜索能力。利用該特性，文獻[10]將量子粒子群優化算法應用于電網規劃問題。在量子粒子群優化算法中設種群規模為M，粒子位置更新方法如下：

P=a×Pbest(i)+(1-a)×Gbest

(9)

其中：Pbest表示粒子個體最佳值；Gbest表示粒子群最佳值；a為一個隨機數，取值范圍為[0,1]。粒子個體最佳值的平均值為：

(10)

在取值空間內，粒子群搜索過程中收縮擴張因子的更新方式如下：

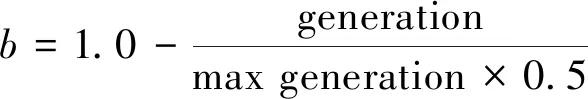
(11)

其中：generation表示當前進化代數；max generation表示最大進化代數。

position=

(12)

其中u為一個隨機數，取值范圍為[0,1]。相比粒子群優化算法，量子粒子群優化算法更容易實現，且所需的調節參數更少。此外，在全局搜索的過程，其陷入局部最優的可能性更低。

2 軟件缺陷預測模型的建立

經研究發現，基于BP神經網絡的軟件缺陷預測模型一般具有較高的概率陷入局部最小值，會導致學習時間長、預測精度差的問題。因此，不少文獻對BP神經網絡進行了各種優化和調整，以提高軟件缺陷模型的預測性能。例如，文獻[11]提出用模擬退火技術代替局部梯度下降法修正BP神經網絡的權值。

2.1 量子粒子群優化BP神經網絡

本文研究目的是使用量子粒子群優化算法改進BP神經網絡各層的連接權值和閾值，從而提高其收斂性能。在確定軟件缺陷預測模型的BP神經網絡結構和相關參數后，采用量子粒子群優化算法對學習結果進行優化，將優化結果反饋到BP神經網絡，從而解決BP神經網絡收斂速度慢、易陷入局部最優的缺陷。BP神經網絡中隱含層采用的應激函數S(z)設置為：

(13)

其中：k表示一個控制應激函數陡峭性的調整因子；z表示該應激函數的輸入值。

量子粒子群優化BP神經網絡算法的實現過程如下：

① 創建BP神經網絡；

② 初始化粒子群，設定種群規模及相關參數并完成迭代過程；

③ 評估粒子的適應度以便得到每個粒子的個體極值和全局極值，并記錄全局極值；

④ 對于每個粒子的極值都要進行實時的更新，如式(12)所示；

⑤ 重新計算每個粒子的適應度，并記錄全局極值；

⑥ 判斷是否滿足收斂條件，是則跳轉下一步，否則繼續執行步驟3；

⑦ 通過獲得的最佳位置對全局最佳值(BP神經網絡各層的連接權值和閾值)進行更新，算法運行結束。

2.2 軟件缺陷預測模型

基于量子粒子群優化BP算法的軟件缺陷預測模型如圖3所示。

3 實例分析

3.1 實驗數據

本文采用NASA提供的MDP 軟件信息數據集(arff文件格式)[12-14]，對基于量子粒子群優化BP算法(QPSO-BP)的軟件缺陷預測模型進行驗證分析和性能對比。具體使用MDP數據集中的7個數據集文件進行了軟件缺陷預測，其相關信息如表1所示。實驗環境：Windows 10操作系統，6 GB內存。在Eclipse平臺上采用Java開發語言進行具體編程實現。設定學習率為0.02，訓練次數為10 000次，最大誤差為0.002。

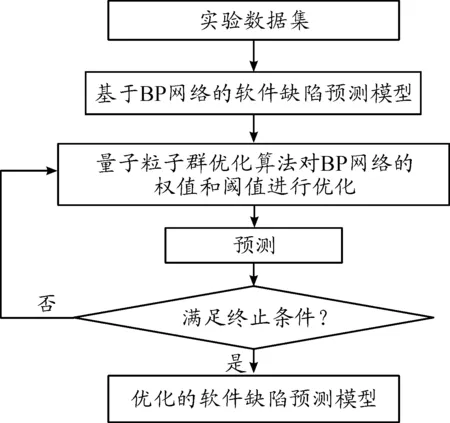
圖3 軟件缺陷預測模型

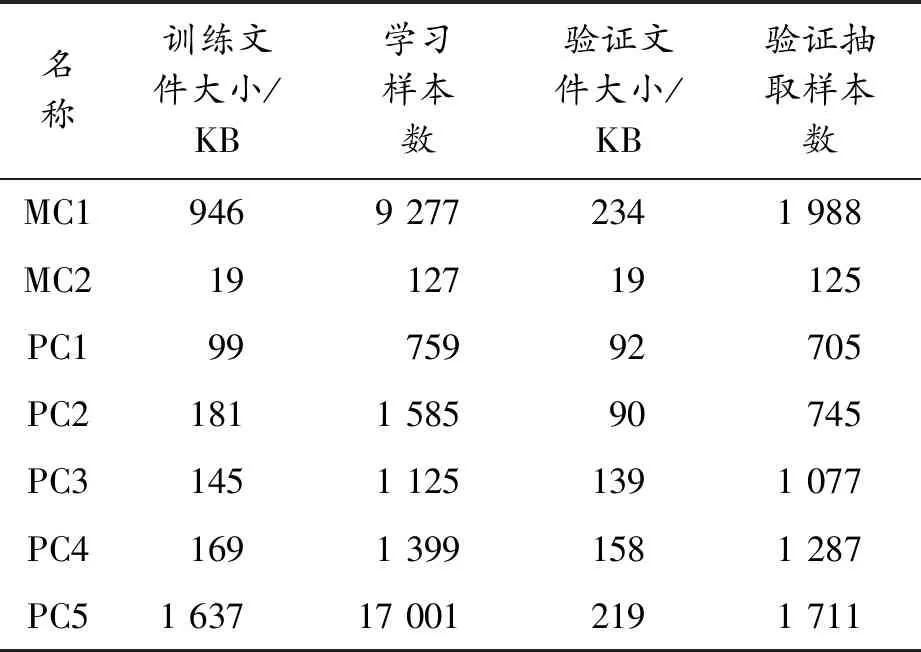
名稱訓練文件大小/KB學習樣本數驗證文件大小/KB驗證抽取樣本數MC19469 2772341 988MC21912719125PC19975992705PC21811 58590745PC31451 1251391 077PC41691 3991581 287PC51 63717 0012191 711

3.2 評估指標

為了對提出模型的性能進行量化分析，選用3種常用的評價準則[15-17]：均值誤差平方和、回歸曲線方程的相關指數和準確度來比較模型的預測能力。均值誤差平方和的計算方法如式(14)所示。

(14)

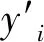
(15)

其中：yave表示yi的均值；RSq的數值越接近1，可靠性評估性能越好。準確度的計算方法如式(16)所示：

(16)

其中：T表示正確預測的模塊數量；C表示觀測數據實例的總數。準確度的數值越高越好。

3.3 結果與分析

表2分別列出了基于傳統BP神經網絡、PSO-BP和QPSO-BP的3種軟件缺陷預測模型在7個數據集文件上的預測結果。

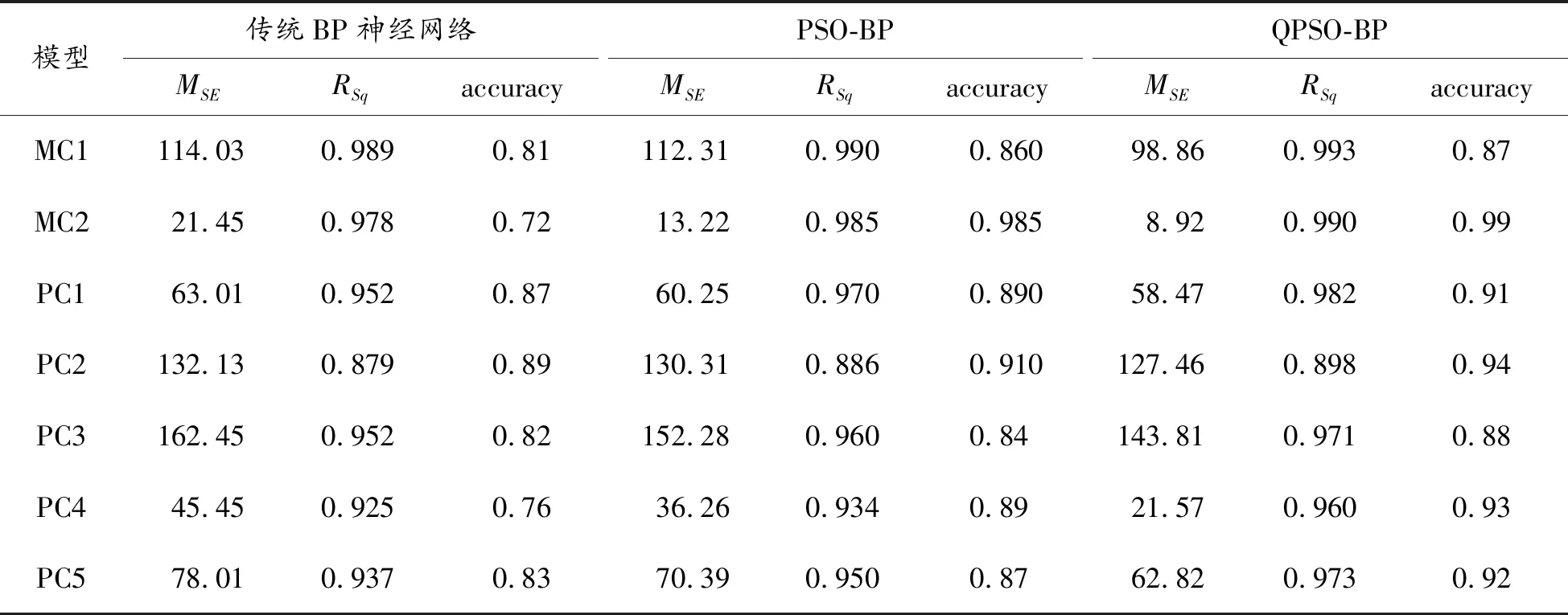
表2 不同模型的預測結果

從7個數據集文件上的預測結果可以看出：相比其他2種基于BP神經網絡的軟件缺陷預測模型，基于量子粒子群優化BP算法的軟件缺陷預測模型的性能最佳，準確度最高。從表2中可以看出：本文提出模型的MSE數值均最小，分別為98.86、8.92、58.47、127.46、143.8、21.57和62.82。RSq數值均接近1，分別為0.993、0.99、0.982、0.898、0.971、0.96、0.973。7組預測的準確度結果也最高，均能達到90%左右。

3種軟件缺陷預測模型的預測計算時間結果如圖2所示。可以看出：相比基于傳統BP神經網絡和PSO-BP的方法，基于量子粒子群優化BP算法的軟件缺陷預測模型所需的學習時間最短。這是由于量子粒子群優化算法更容易實現，且所需的調節參數更少。

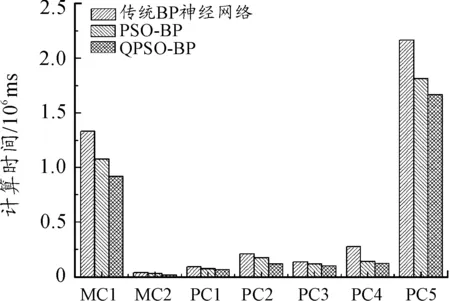
圖4 軟件缺陷預測的計算時間對比

4 結束語

本文將量子粒子群算法和BP神經網絡相結合，提出了一種基于QPSO-BP的軟件缺陷預測模型。提出的優化方法能更有效地提高BP神經網絡的收斂速度，防止陷入局部極小。仿真實驗結果顯示：相比傳統BP神經網絡和粒子群優化BP神經網絡，提出軟件預測模型的準確率、效率均得到有效提高。但是，提出算法的預測精度仍有提升空間，后續將會對BP神經網絡結構和參數做進一步改進和優化。