面向無人機集群的數據鏈中繼節點選擇方法

2019-07-22 01:08:00鄒永顯鄒浩彥

艦船電子對抗 2019年3期

肖剛，鄒永顯，王雷，鄒浩彥

(1.中國電子科技集團公司第二十研究所，陜西西安 710068；2.解放軍63963部隊,北京 100072；3.中航飛機股份有限公司特設技術室，陜西西安 710089；4.解放軍駐西飛公司軍事代表室，陜西西安 710089)

0 引言

無人機集群具有協同能力強、任務執行單元多、成本相對低等特點，適合在復雜環境下完成搜索、偵察、打擊等任務[1]。但無人機受限于其單機抗毀性差和覆蓋范圍有限等缺點，需要無人機集群數據鏈通信解決。在任務執行期間，無人機集群位置有隨機性、分散性等特征，某些無人機平臺在任務中會出現遠離集群、獨立執行任務的情況，因此，無人機集群分散機動中通信問題成為無人機集群通信領域的一個研究方向[2]。隨著無人機的種類逐漸豐富，出現了續航能力長、通信距離遠的無人機機型，可以有效解決以上問題。具有中繼無人機的無人機數據鏈網絡，可以顯著擴展集群執行任務的通信范圍，靈活建立編隊子網，有效控制孤立的無人機單元，實現整個集群態勢資源共享，增強集群編隊協同能力[3]。本文綜合考慮，以無人機集群協作執行任務為背景，構建了無人機集群數據鏈中繼網絡，設計基于文化算法的改進克隆蟻群算法解決無人機數據鏈中繼節點選擇問題。

1 中繼節點選擇相關研究

無人機中繼節點的通信區域主要取決于中繼節點飛行高度、通信區域高度和最大通信距離[4]。假設最大通信距離為R,中繼節點飛行高度為H，通信區域高度為h，則通信最大覆蓋半徑為：

(1)

在實際作戰中，無人機集群節點間高度差一般在數十米到數千米間，而中繼節點的最大通信距離往往高達幾百千米以上，節點間的高度差對比與通信最大距離可以忽略不計。考慮到無人機間的高度差對于信號的通信范圍和集群拓撲結構的影響可以忽略，故為便于建模分析問題，本文將節點選擇問題從三維空間降維到二維空間進行研究。

1.1 通信覆蓋率

本文將任務區域按照網格形式分解，并將每一個網格簡化為點，成為像素點，設任務區域有m×n個像素點，節點集S通信覆蓋率Rarea(S)為S覆蓋像素點的總和與任務區域總像素點的比值公式如下：

(2)

1.2 聚集度

聚集度的衡量標準是節點之間的平均最短路徑和網絡中的節點數目[5]。聚集度是用于評估在中繼節點數量有限和通信距離有限的情況下，如何部署可以既滿足覆蓋和通信的需求，又可以最大限度地提升網絡抗毀性。在無人機集群中，每個中繼無人機除了對本身通信范圍內的無人機進行中繼，同時要考慮為相鄰無人機轉發消息。因此，本文定義中繼無人機的聚集度βi：

(3)

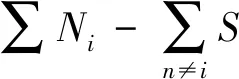
1.3 分布評估函數

在中繼無人機數量和覆蓋半徑確定的條件下，基于集群連通性、魯棒性和覆蓋率，在保證集群最佳通信覆蓋的情況下，為增強數據鏈網絡的魯棒性，各中繼無人機的聚集度需要盡量小。3個條件間相互制約，綜合衡量得到數據鏈中繼網絡的分布評估函數為：

Edis=l1×Rarea(S)-l2×var(βi)

(4)

式中：l1和l2為權重系數。

2 CA-CSACA算法設計

2.1 蟻群算法

假設螞蟻k由當前節點i移動到節點j的移動規則為:

(5)

式中：α為第k只螞蟻移動中信息素濃度；β為啟發因子在螞蟻挑選節點中的重要度；dk為螞蟻k可以下一步選擇的節點子集；ηij(t)為挑選節點的啟發信息；τij(t)為在t時刻路徑(i,j)上的信息素量。

為防止信息素殘留引起啟發信息作用被削弱，當螞蟻選擇下一步節點后，要對信息素進行局部更新，更新公式如下：

τi,j(t+Δt)=(1-ρ1)τi,j(t)+Δτi,j(t)

(6)

(7)

(8)

式中：0

當沒有局部更新時，螞蟻將在上一次選擇的最佳路徑的相鄰區域內搜索。

2.2 克隆選擇算法

克隆選擇算法基本操作如下：

(1) 復制操作：將Ai(k)復制qi次，生成qi個抗體，這一操作表示為：

(9)

式中：Ei為qi×1的單位陣。

抗體適應度qi為：

qi(k)=g(N，f(Ai(k)))，1≤i≤n

(10)

(11)

式中：Int(·)為取最小整數的函數；N(N>n)表示克隆數目。

由此可見qi與f(Ai(k))成正比例關系。通過克隆復制操作后，種群變為Y(k)，形式如下：

Y(k)={Y1(k)，Y2(k)，…，Yn(k)}

(12)

式中：Yi(k)={Ai1(k)，…Aij(k)，…，Aiqi(k)}，且Aij(k)=Ai(k)，j=1，2，…，qi。

(13)

(14)

一般使用概率選擇的方法，進行進化操作。

具體地，?i=1,2,…,n，則：

Bi(k)=max{Zi(k)}=

{zij(k)|max(f(Zij))，j=1，2，…，qi}

(15)

Bi(k)取代Ai(k)成為Ai(k+1)的概率Ps為：

(16)

其中根據計算種群中各抗體適應度值，挑選出適應度值最大的抗體作為最優抗體。

2.3 文化算法

文化算法模擬人類知識積累的歷程，在普通種群空間的基礎上構建有知識積累、進化和傳播的信仰空間，形成雙層進化機制[7]。文化算法主要包括三部分，分別是種群空間、信仰空間與溝通渠道。其中溝通渠道可具體劃分為接受函數、影響函數和更新函數。而信仰空間則主要包括規范知識、拓撲知識、領域知識等[4]。接受函數提取每一個代種群中適應度高的個體，并送入樣本庫進行演化。

2.4 CA-CSACA算法

蟻群算法求解過程中容易過早得到局部最優解并局部收斂。克隆選擇算法通過免疫和克隆操作，可以不斷給種群引入新的優秀個體，有利于跳出局部收斂，而得到全局最優解。2種算法通過文化算法的雙層進化機制有機結合，建立以克隆選擇算法優化的信仰空間和以蟻群算法優化的種群空間。經克隆選擇算法初始化信仰空間、蟻群算法優化種群空間處理后，采用適應度函數評估種群中個體適應度優劣，通過接收函數將迭代中產生的最優個體保存在信仰空間，信仰空間使用克隆選擇算法定期將保存的優良個體通過影響函數反饋到種群空間，種群空間在更新后的新種群基礎上繼續進化，重復整個進化過程，直到滿足結束條件，得到最優解。

算法流程描述如下：

步驟1：種群空間初始化，采用蟻群算法進化，設置基本參數，如螞蟻數量、信息素揮發系數、迭代次數等。根據適應度公式評估抗體的優劣。

步驟2：信仰空間初始化，采用克隆選擇算法進化，形成抗體的種群，針對抗體種群，分別進行交叉和變異操作，操作數量占種群空間個體數量的15%到25%。

步驟3：定義接受函數，在每輪進化結束后，信仰空間用種群空間中當前最優解替換信仰空間內當前最劣解。

步驟4：定義影響函數，每迭代N次，用信仰空間中適應度最優的T個個體將種群空間中適應度最差的T個個體進行替換。

步驟5：迭代求解：

(1) 種群空間更新。當滿足條件時，運行影響函數，然后利用蟻群算法對種群空間進行進化。

(2) 信仰空間更新。運行接受函數，然后利用克隆選擇算法對信仰空間進行進化。

步驟6：更新記錄冊。每次迭代完成后比較當前記錄冊的值和種群空間中的最優值，并將兩者中的較優值賦給記錄冊。

步驟7：比較終止條件和記錄冊上的值，直至滿足終止條件，輸出解集；否則，轉步驟5。