高速角接觸球軸承剛度計算及影響因素分析
丁鴻昌,李家成,李茂源,付會彬
(山東科技大學 機械電子工程學院,山東 青島 266590)
符號說明
A——內、外溝曲率中心距
B——軸承寬度
d——內徑
d′i——內圈溝道直徑
d′e——外圈溝道直徑
D——外徑
Dpw——球組節圓直徑
Dw——球直徑
Eb——外圈材料彈性模量
Eh——軸承座材料彈性模量
fe——外溝曲率半徑系數
fi——內溝曲率半徑系數
F——外載荷
Fc——球離心力
j——第j個球
J——球轉動慣量
K——軸承剛度
K′——球與套圈接觸剛度
m——球質量
M——傾斜力矩
Mg——球陀螺力矩
Q——球與套圈的接觸力
Ri——內圈溝道半徑
t——時間
X——外溝曲率中心與球心之間的距離
Z——球數量
Δf1——軸與內圈過盈量
Δf2——軸承座與外圈過盈量
ωb——球公轉角速度
ωr——球自轉角速度
ωc——保持架角速度
δ——內、外圈相對位移
δ′e——外圈溝道直徑減小量
δ′i——內圈溝道直徑增大量
θ——內、外圈角位移
α——接觸角
ψ——球方位角
ζ——球姿態角
νb——外圈材料泊松比
νh——軸承座材料泊松比
μ——摩擦因數
x,y,z——坐標軸方向
下標
i——內圈
e——外圈
角接觸球軸承是旋轉機械的重要零部件,具有摩擦力小,潤滑簡單和便于更換的優點,廣泛應用于汽車、機床、精密儀器、航空航天、機器人等領域。隨機械工業的發展,旋轉機械朝著高精度,高速度,重載荷的方向發展,為滿足旋轉機械設備的要求,并確保系統的安全性和可靠性,有必要提高軸承在高轉速工況下的支承性能[1-4]。
文獻[5]基于簡單的力學關系和理想的運動狀態建立了滾動軸承平衡方程,并分析了軸承在任意工況下的載荷分布;文獻[6]對低速時靜態軸承內部的載荷分布及高速時動態軸承的內部載荷分布進行了分析;文獻[7]基于ANSYS/LS-DYNA建立了角接觸球軸承有限元模型,分析了軸承應力分布和動態響應;文獻[8]建立了滾動軸承接觸力學模型,采用組合曲面積分和有限元法求解滾動體和滾道之間的接觸力;文獻[9]分析了軸承動力學模型中載荷與撓度的關系,并提出了一種基于隱函數微分的解析模型用來計算剛度;文獻[10]分析了不同軸承配置下的主軸承剛度。
在上述研究的基礎上,以某角接觸球軸承為研究對象,綜合考慮了高轉速下球的離心力、陀螺力矩等參數的影響,建立了一個五自由度的角接觸球軸承剛度模型,分析軸向載荷、徑向載荷、轉速和過盈量等因素對軸承剛度的影響。
1 角接觸球軸承建模
以NSK 7212A5角接觸球軸承為研究對象,其主要結構參數見表1。軸承內、外圈和球材料均為GCr15軸承鋼,其材料參數為:彈性模量207 GPa,泊松比0.3,密度7 830 kg/m3,屈服應力1 815 MPa。
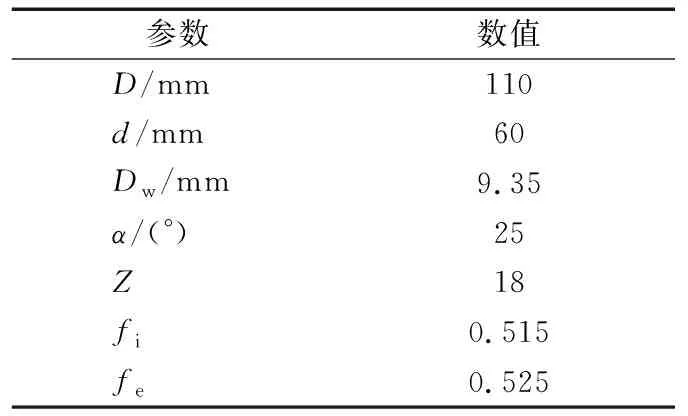
表1 7212A5角接觸球軸承主要結構參數
在CAD中建立該角接觸球軸承的二維模型,如圖1所示。為建立實用的軸承模型,提出以下假設[11-12]:1)外圈固定,內圈會產生徑向或軸向偏轉;2)外圈和內圈不彎曲,在球和溝道的接觸區域處會發生小變形,但不會影響2個溝道的整體形狀;3)球由保持架以恒定角度分開,忽略保持架動態行為;4)外載荷作用在套圈上,不會導致軸承套圈出現角度不對中;5)忽略潤滑,軸承在等溫條件下運轉。
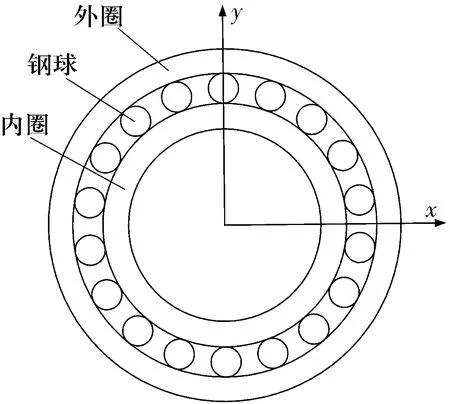
圖1 角接觸球軸承二維模型
2 軸承動態剛度計算
軸承動態剛度是指在交變動載荷作用下抵抗動態位移的能力,是軸承在運動過程中的瞬時剛度,體現為球與溝道的接觸剛度[13-14]。
2.1 過盈配合分析
軸承在安裝過程中采用過盈配合,內圈溝道直徑增大,外圈溝道直徑減小[15]。根據彈性力學可得
(1)
δ′e=
(2)
在軸承安裝后,初始接觸角α0變為α,則
(3)
2.2 平衡方程
接觸角作為角接觸球軸承的重要參數之一,大多數情況下為一個常量,稱為公稱接觸角。軸承運轉時,接觸角會發生變化。為使軸承載荷分布計算更為精確,必須考慮其接觸角變化[16]。
第j個球中心與內、外溝曲率中心的位置關系如圖2所示,對軸承施加載荷后,外溝曲率中心A保持不變,而內溝曲率中心從C移動到C′,球中心從O移動到O′,球與外溝道的接觸角由α變為αej,與內溝道的接觸角從α變為αij。
通過引入A1j,A2j,X1j,X2j輔助變量來描述圖2的幾何關系,即
(A1j-X1j)2+(A2j-X2j)2-[(fi-0.5)Dw+δij]2=0,
(4)
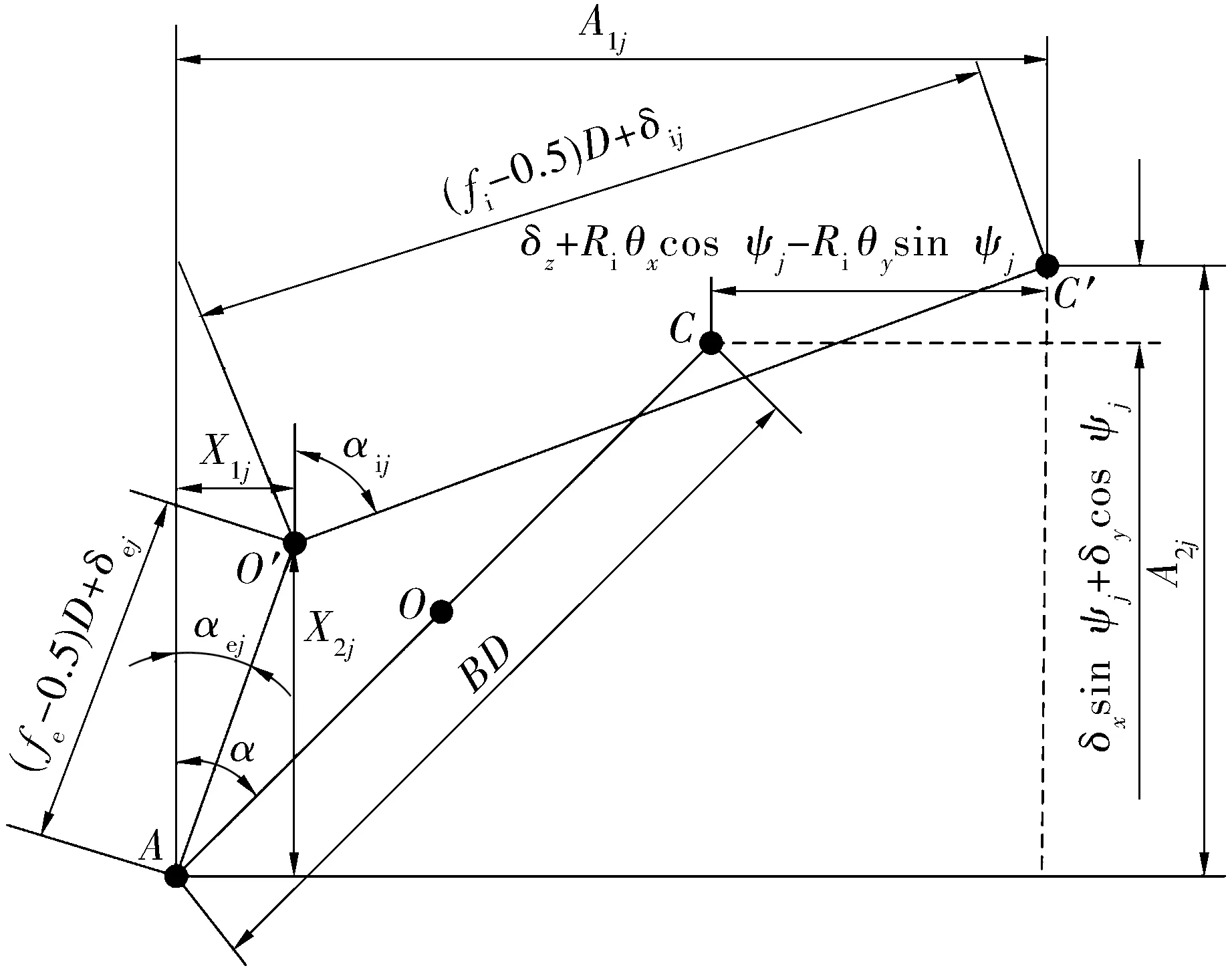
圖2 球和溝曲率中心的位置關系示意圖
考慮軸承五自由度,輔助變量A1j,A2j可表示為
A1j=BDsinα+δz+Riθxcosψj-Riθysinψj,
(5)
A2j=BDcosα+δxsinψj+δycosψj,
(6)
對于任意方位角的球,根據溝道控制理論,假設球的陀螺力矩可通過球與溝道之間的摩擦力并應用D′Alembert原理來平衡,如圖3所示。
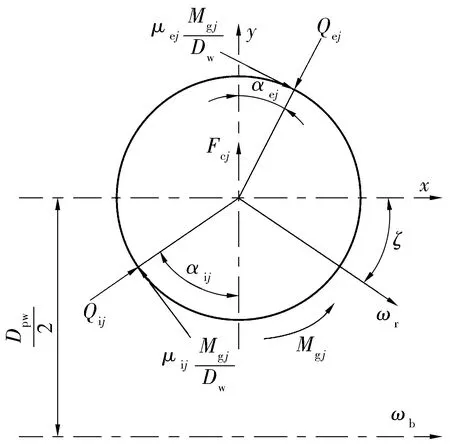
圖3 球的受力分析圖
球的力和力矩平衡方程為
(7)
μij+μej=1。
根據Hertz接觸理論確定球與內、外圈溝道的接觸力為
(8)
球的離心力和陀螺力矩分別為
(9)
Mgj=Jωrωbsinζ;j=1,2,…,Z,
(10)
力和力矩作用下的軸承位移如圖4所示,由于軸承載荷及球位置變化,這2個接觸角可表示為
。 (11)
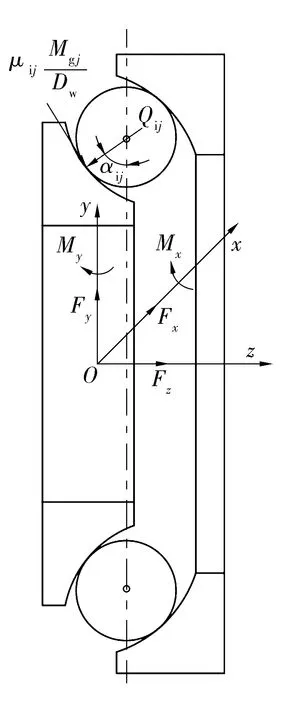
圖4 力和力矩作用下的軸承位移
Jones-Harris模型由3部分組成,即軸承零部件幾何約束關系,球力平衡和內圈力平衡,該傳統模型僅x,y,z這3個平動自由度。在該模型基礎上,增加軸承內圈繞x,y軸的2個角位移,對5個自由度軸承模型進行分析。
考慮到球對內圈溝道的作用,軸承整體平衡方程為
(12)
2.3 軸承剛度矩陣
基于準靜態模型的增量法計算五自由度剛度矩陣,即
(13)
式中:Kxx,Kyy為徑向剛度;Kzz為軸向剛度;Kθxθx,Kθyθy為角剛度。
在剛度矩陣K中,其他剛度元素相比于對角元素影響很小,分析中可忽略。對角元素可表示為
(14)
(4),(7),(12)式可通過Newton-Raphson法求解,最終通過(13),(14)式可計算軸承剛度矩陣。通過剛度矩陣中主對角線的剛度值可得到軸向剛度Kzz、徑向剛度(Kxx=Kyy)、角剛度(Kθxθx=Kθyθy)。
3 模型驗證
以NSK 7020A5型單列角接觸球軸承為研究對象,在預載荷分別為450,1 100,2 200 N時進行理論計算,得到不同預載荷下軸承的剛度為
K450=

K1 100=

K2 200=

軸承理論剛度計算值與文獻[17]中的試驗結果對比見表2,由表可知,二者相對誤差在8%以內,說明建立的軸承剛度計算模型是可靠的。
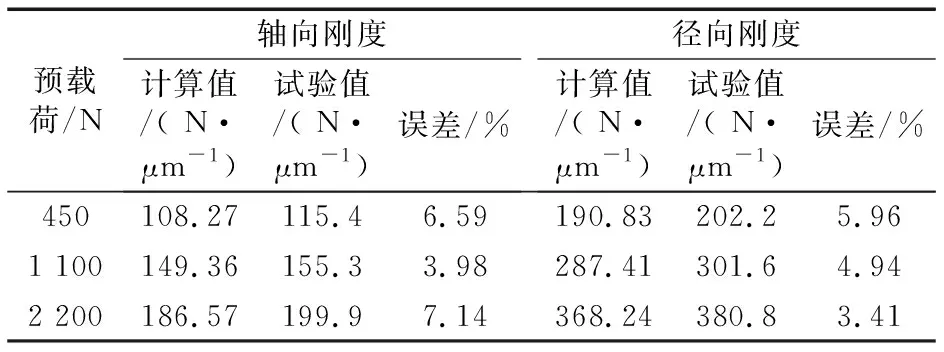
表2 軸承剛度計算值與文獻中試驗結果對比
4 結果分析
在上述理論研究的基礎上,分析NSK 7212A5軸承軸向載荷Fa、徑向載荷Fr、轉速n和安裝過盈量Δ對軸承剛度的影響。
4.1 軸向載荷對軸承剛度的影響
在Fr=0 N,Δ=5 μm,n=10 000 r/min下,軸承剛度隨軸向載荷的變化如圖5所示,由圖可知:當軸向載荷增大時,徑向剛度、軸向剛度和角剛度均增大,且三者曲線均為非線性,增大幅度隨軸向載荷增大而減小。
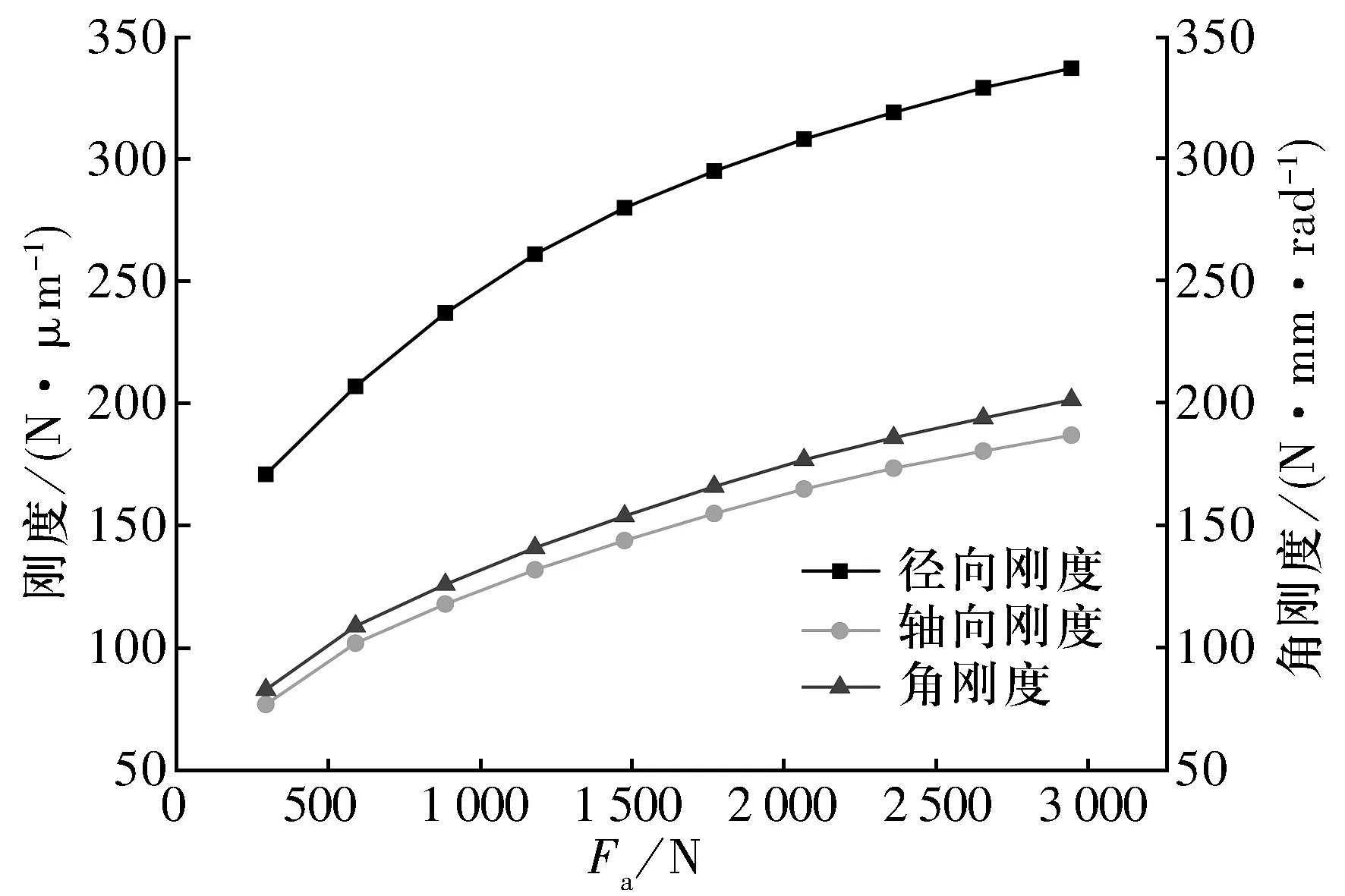
圖5 軸承剛度隨軸向載荷的變化
4.2 徑向載荷對軸承剛度的影響
在Fa=295 N,Δ=5 μm,n=10 000 r/min時,軸承剛度隨徑向載荷的變化如圖6所示,由圖可知:隨徑向載荷增大,軸向剛度和角剛度逐漸減小,但變化緩慢;而徑向剛度增大,且增大趨勢較為明顯。這是由于徑向載荷增大時,軸承內部游隙和球間距變大,接觸區球數量逐漸減少。
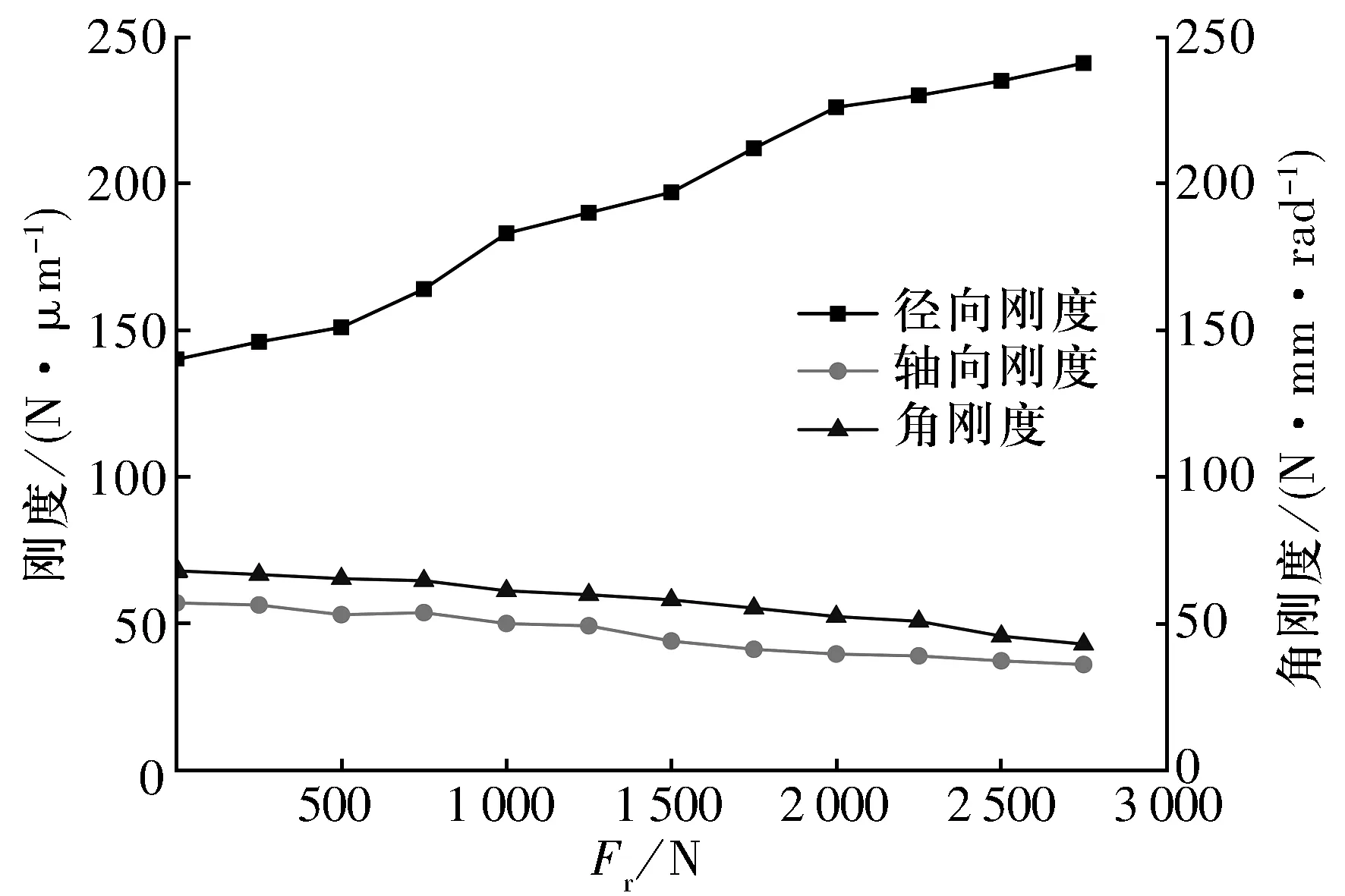
圖6 軸承剛度隨徑向載荷的變化
4.3 轉速對軸承剛度的影響
在Fr=0 N,Fa=295 N,Δ=5 μm時,軸承剛度隨轉速的變化如圖7所示,由圖可知:隨軸承轉速增大,徑向剛度減小,軸向剛度和角剛度先減小后趨于穩定。這是由于軸承轉速增大后,球離心力迅速變大,使軸承內、外圈溝道間隙變大,導致球與外圈溝道之間的接觸角和接觸剛度減小。當轉速增大到某值時,受軸承結構限制,鋼球離心力引起的軸承溝道變形趨于穩定,徑向剛度減小變緩,軸向剛度和角剛度也趨于穩定。

圖7 軸承剛度隨轉速的變化
4.4 過盈量對軸承剛度的影響
在Fr=0 N,Fa=295 N,n=10 000 r/min時,軸承剛度隨過盈量的變化如圖8所示,由圖可知:隨安裝過盈量增大,軸承徑向剛度變大,軸向剛度和角剛度則先減小后趨于穩定。這是由于過盈量增大,軸承內部間隙減小,球與內、外圈溝道的接觸剛度增大,而球與內、外圈溝道的接觸角減小。當過盈量增大到某值時,受軸承結構限制,軸承內、外圈溝道變形趨于穩定,徑向剛度增大變緩,軸向剛度和角剛度也趨于穩定。
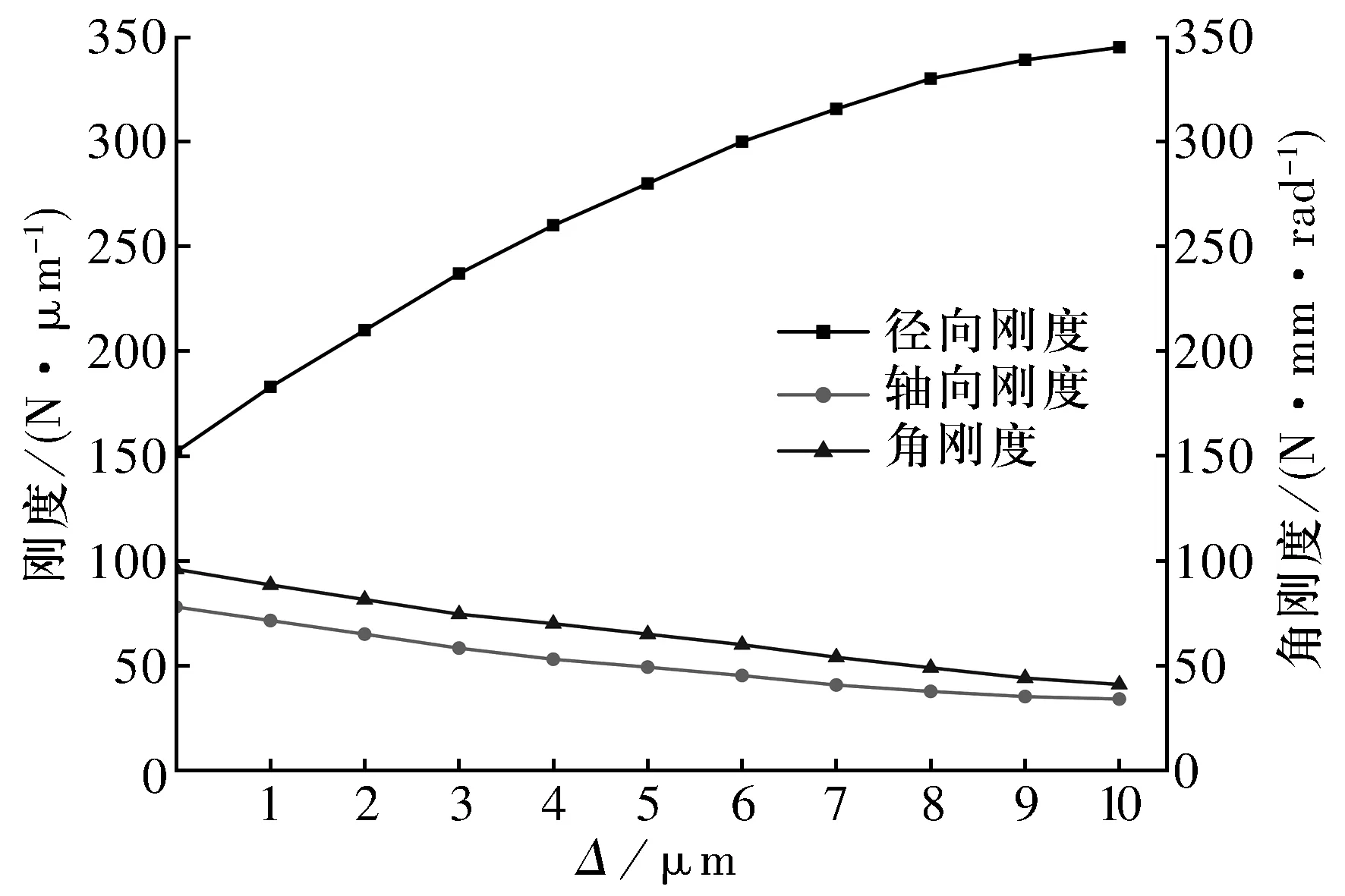
圖8 軸承剛度隨過盈量的變化
4.5 小結
轉速和徑向載荷屬于軸承使用條件,因而軸承預期剛度可通過設定軸向載荷和過盈量得到。在Fr=0 N,n=10 000 r/min時,Fa及Δ綜合作用對軸承剛度的影響如圖9所示,由圖可知:當Fa和Δ增大時,徑向剛度也隨之變大。因此,在實際工況下可根據軸向預緊力的推薦數值和過盈量來選擇軸承剛度的工作范圍。在低速、輕載工況下,盡量選用較小的安裝過盈量及軸向預緊力;在高速、重載工況下,盡量選用較大的安裝過盈量及軸向預緊力。
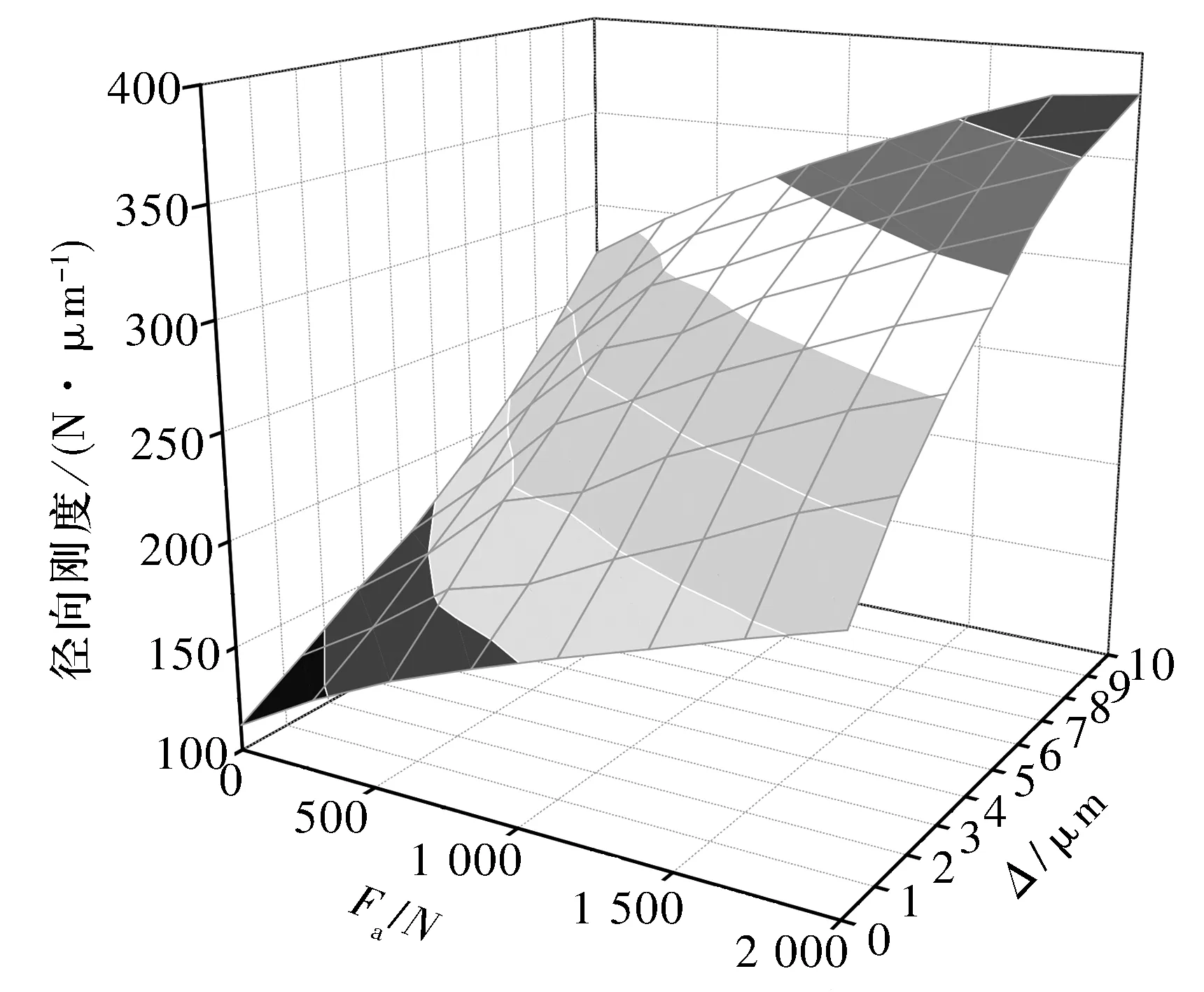
圖9 軸向載荷及過盈量綜合作用對軸承剛度的影響
5 結束語
在Jones-Harris剛度模型的基礎上建立了一個基于溝道控制理論的五自由度角接觸球軸承剛度計算模型,該模型計算值與試驗值相對誤差在8%以內,證明了該模型的可靠性。并分析了軸向載荷、徑向載荷、轉速和安裝過盈量對軸承剛度的影響,實際工況下可根據軸向預緊力的推薦數值和過盈量來選擇軸承剛度的工作范圍。

