考慮表面缺陷的角接觸球軸承非線性動力學分析

殷學賓，趙自強，王文中

(北京理工大學 機械與車輛學院，北京 100081)

滾動軸承作為機械設備重要的支承部件，其動態特性直接影響整機的性能。隨著重要裝備向高速、高精度方向發展，對滾動軸承的精度、可靠性和承載特性提出了越來越高的要求。然而，在軸承的加工制造和服役過程中，滾道表面會產生凹坑、凸包、劃痕、裂紋、剝落等缺陷，引起軸承振動，影響機械設備的運轉精度。因此，有必要對滾動軸承進行故障動力學建模，分析其在特定工況和故障下的動力學行為規律，為狀態監控和故障診斷提供理論依據。

文獻[1-2]首次提出了考慮缺陷的滾動軸承的分析模型，研究了內溝道表面單個和2個點缺陷對軸承振動的影響。模型中用一系列的脈沖代替鋼球通過缺陷時的動態響應，通過試驗證明了模型的正確性。文獻[3]建立了分析模型，研究了位于內、外滾道或者滾動體上的單個缺陷引起的軸承振動頻率，考慮了徑向和軸向載荷，并采用矩形、三角形和半正弦脈沖表示缺陷引起的振動響應。文獻[4-5]建立了六自由度的深溝球軸承動力學模型，考慮了非線性Hertz接觸變形和彈流潤滑油膜，研究了局部式缺陷和分布式缺陷對軸承振動的影響，發現徑向游隙對軸承系統的振動響應和固有頻率有較大的影響。文獻[6]基于有限元軟件研究了不平衡受力狀態下局部式缺陷對滾動軸承振動的影響。文獻[7]建立了求解局部表面缺陷對軸承振動問題的數值模型，其中加入了滑動摩擦的影響。文獻[8]建立了軸-軸承模型，研究了角接觸球軸承有缺陷和無缺陷對球振動的影響。文獻[9]基于Runge-Kutta法建立了求解深溝球軸承單一缺陷、多缺陷及缺陷位于內、外溝道引起的軸承振動的模型。文獻[10-11]考慮了缺陷引起的時變位移和時變接觸剛度，并將缺陷形狀劃分得更加細致。文獻[12]研究了鋼球通過局部表面損傷時軸承的加速度與鋼球、損傷之間沖擊力的對應關系，以及轉速和損傷寬度對軸承振動響應的影響規律。文獻[13]建立了角接觸球軸承非線性動力學模型，研究了質量、剛度對系統穩定性的影響。文獻[14]建立了含有單表面故障的滾動軸承非線性動力學方程，對缺陷軸承連續運轉過程進行了分析。文獻[15]建立了深溝球軸承局部剝落故障時變位移激勵模型，研究了球通過局部剝落缺陷過程中的打滑動力學特征。

多數文獻以深溝球軸承為研究對象，且缺陷數目多是1個和2個，而缺陷對角接觸球軸承振動特性的影響鮮有研究。然而，角接觸球軸承廣泛應用于機床主軸等各種裝備中，且缺陷數目、分布規律是均勻或隨機的。因此，現以角接觸球軸承為研究對象，結合Hertz接觸理論，運用4階Runge-Kutta法求解運動學微分方程，結合位移頻譜圖，研究缺陷對角接觸球軸承振動的影響。

1 考慮缺陷的角接觸球軸承動力學建模

1.1 動力學模型

角接觸球軸承承受純軸向載荷Fa作用時，各球受力均勻，其大小為

(1)

式中：Z為球數；α為軸向載荷作用下的接觸角，其值大于初始接觸角α0。

純軸向載荷作用下軸承接觸角的變化示意圖如圖1所示。

圖1 純軸向載荷作用下接觸角的變化

當軸承承受軸向載荷時，內圈只發生軸向位移。球與溝道之間的變形量δ是內、外溝曲率中心距的變化量，由圖1可知

δ=EI′-EI，

(2)

EIcosα0=EI′cosα，

(3)

(4)

式中：A為內、外溝曲率中心距。由此可得

(5)

根據Hertz接觸理論，球與溝道間的接觸力為

(6)

式中：K為軸承剛度。

將(1)式代入(6)式可得

(7)

用數值迭代法可求得α。

內圈只發生軸向位移δ0(圖1中的II′)，由圖1可得

(8)

(9)

通常假設外圈剛性且固定不動。在軸向和徑向載荷作用下，內圈中心在徑向平面內豎直方向上的位移為x，水平方向上的位移為y，在軸向平面內的軸向位移為z。軸承徑向平面示意圖如圖2所示。

圖2 軸承徑向平面示意圖

在任意時刻t，徑向平面內內圈中心的位移為

δrj=xcosφj+ysinφj，

(10)

φj=2π(j-1)/Z+ωct，

式中：φj為t時刻第j個球的位置角；ωc為球的公轉角速度；ωi為內圈角速度；di和de分別為內、外圈溝底圓直徑。

內圈中心在軸向上的位移為

δaj=z。

(11)

在φj處，球與溝道間總的彈性變形量為內、外溝曲率中心距的變化量

δj=A′-A，

(12)

式中：A′為受載后內外溝曲率中心距。

根據幾何關系

(13)

根據Hertz接觸理論，第j個球與溝道間的接觸力為

(14)

所有球作用于內圈上的接觸力分解到x，y，z方向為

(15)

根據Lagrange方程，建立軸承-轉子系統的運動微分方程為

(16)

式中：m為轉軸和內圈的總質量；c為阻尼系數，e為軸承-轉子系統的偏心距，當系統平衡時e取0；Fx，Fy，Fz為油膜切向摩擦力F在x，y，z方向上的分力；Fr為徑向載荷。

滑滾接觸中潤滑油膜的切向摩擦力隨滑滾比的變化較為復雜，可用經驗摩擦因數法[16]計算鋼球與溝道間潤滑油膜的切向摩擦力。為了簡化計算，取摩擦因數μ=0.007。接觸區內任一點的摩擦切應力為

(17)

式中：a，b分別為接觸區的長、短半軸。切應力在接觸區內積分可以得到總的油膜切向摩擦力。

令

(18)

(16)式可化簡為一階非線性微分方程組，即

(19)

(19)式可采用4階Runge-Kutta法求解。

1.2 表面缺陷模型

溝道缺陷示意圖如圖3所示，圖中：ζ為缺陷位置角，下標i，e分別為內、外溝道；dw為缺陷的寬度；dq為缺陷深度；Dw為球徑；Δ為球中心的變化高度，當球落入缺陷中，有

圖3 溝道缺陷示意圖

(20)

具有多個缺陷的滾動軸承示意圖如圖4所示。

圖4 多個溝道缺陷的軸承示意圖

由于外圈固定，外圈上的缺陷位置保持不變

(21)

(22)

內溝道表面的缺陷隨著內圈以角速度ωi旋轉，t時刻缺陷位置角范圍為

(23)

當內溝道表面有多個缺陷時，第n個缺陷的位置角范圍為

(24)

通過計算球位置和缺陷位置角范圍，可以判斷球和缺陷的相對位置。用β表示球和缺陷的位置關系，當球落入缺陷中，β取1；否則，β取0，即

(25)

(26)

考慮溝道表面缺陷后，球與溝道間的彈性變形量為

δj=A′-A-βiΔi-βeΔe。

(27)

將(27)式代入(14)式即可建立考慮溝道表面缺陷的角接觸球軸承非線性微分方程，仍用四階Runge-Kutta法求解。

2 結果與分析

計算時，x，y，z方向上的位移和速度初值均取0，即z1=z2=z3=z4=z5=z6=0。積分步長取激勵周期的1/1 000，總共計算500個周期，從第450個周期開始取值，即可得到系統穩定后內圈中心在x,y,z方向上的位移和速度。以ZYS 7008C角接觸球軸承為例，其計算參數見表1。

表1 軸承計算參數

將內圈(軸承)轉速作為系統的分岔參數，其變化范圍取5 000～13 000 r/min。軸承位移隨轉速變化的分岔圖如圖5所示，其中圖5a為無缺陷軸承，圖5b和圖5c分別為內、外溝道表面有1個2 mm寬的凹坑缺陷的軸承。由圖可知，無缺陷軸承僅在轉速為5 500 r/min附近出現了1個較短的混沌期，其他轉速下均為單周期運動，當缺陷出現時，單周期運動被破壞;當缺陷位于內溝道時，多周期運動和混沌運動交替出現，軸承振動較為嚴重；當缺陷位于外溝道時，分岔圖比內溝道缺陷的清晰，但比無缺陷軸承的復雜。

圖5 軸承位移隨轉速變化的分岔圖

取內圈轉速為10 000 r/min，研究高速狀況下溝道表面缺陷對軸承運轉精度的影響。軸承特征頻率見表2。

表2 軸承的特征頻率

2.1 缺陷位置的影響

不同缺陷位置下軸承速度-位移相圖和頻譜圖如圖6所示。由圖可知，無缺陷軸承的速度-位移相圖為封閉的橢圓形曲線，表示系統做單周期運動，振動只發生在fve及其倍頻。當溝道表面出現缺陷時，相圖較為雜亂，周期運動被破壞。對比圖6b和圖6c可知，缺陷位于內溝道時對軸承振動的影響較大，這是因為球通過內圈缺陷的頻率(fvi)大于球通過外圈缺陷的頻率(fve)，此外，其頻譜圖的幅值明顯高于缺陷位于外溝道頻譜圖的幅值，且出現了fvi和更多低頻低幅值振動。當缺陷位于外溝道時，頻譜圖中除了有fve及其倍頻，還出現了10fc以及其他低頻率的幅值。

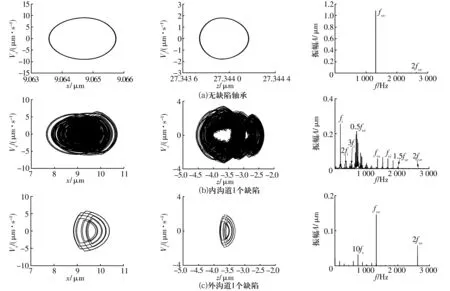
圖6 不同缺陷位置下軸承速度-位移相圖和頻譜圖

2.2 缺陷數目的影響

內溝道上不同缺陷數目的軸承速度-位移相圖和頻譜圖如圖7所示。由圖可知，隨著缺陷數目的增加，速度-位移相圖更加復雜，范圍增大，說明振動增強；頻譜圖也更加復雜，fvi等特征頻率的幅值較單個缺陷明顯增大。

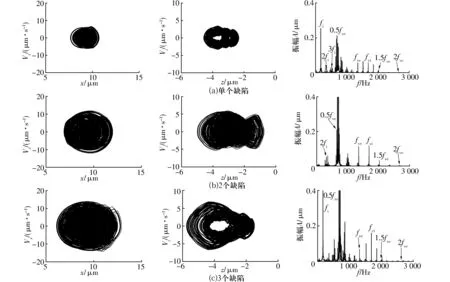
圖7 內溝道不同缺陷數目的軸承速度-位移相圖和頻譜圖

2.3 缺陷分布規律的影響

溝道表面出現多個缺陷時，其分布可能是均勻或隨機的。以3個缺陷為例研究缺陷的分布規律對軸承振動的影響。缺陷均勻分布表示3個缺陷相隔120°分布在溝道表面;缺陷隨機分布表示3個缺陷隨機出現在溝道的不同位置。

內溝道缺陷不同分布規律對軸承振動的影響如圖8所示。由圖可知，相對于缺陷隨機分布，當缺陷均勻分布時，速度-位移相圖更加復雜，范圍更大，軸承振動嚴重，說明缺陷均勻分布加劇了軸承振動。這是因為ZYS 7008C軸承有18個鋼球，當缺陷均勻分布時，每次有3個球同時落入缺陷中，產生共振，軸承振動增大。當缺陷隨機分布時，一般不會出現球同時落入缺陷的情況，一定程度上對軸承振動起到了抑制作用。從頻譜圖可以看出，當缺陷均勻分布時，出現類似于周期性的高幅值頻率，且幅值較大；當缺陷隨機分布時，不存在周期性高幅值頻率，也說明了缺陷均勻分布時軸承周期性振動較強。

圖8 內溝道缺陷分布規律的影響

外溝道缺陷不同分布對軸承振動的影響如圖9所示。由圖可知，外溝道缺陷的不同分布對軸承振動幾乎沒有影響。這是因為外圈是固定的，位于承載區的缺陷對軸承振動起主導作用，而分布規律對其影響相對較小。二者的頻譜圖基本相同，也表明外溝道缺陷的不同分布對軸承振動幾乎沒有影響。

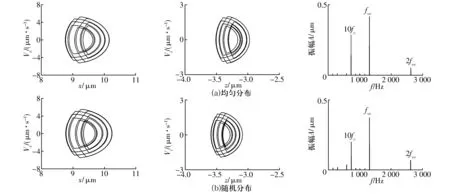
圖9 外溝道缺陷分布規律的影響

3 結論

1)溝道表面凹坑缺陷降低了角接觸球軸承的運轉精度，且缺陷位于內溝道時，軸承振動較為嚴重。

2)溝道表面多個缺陷會使軸承振動加劇，相對于缺陷均勻分布，缺陷隨機分布對軸承振動起到一定的抑制作用。

3)外溝道表面產生缺陷時，頻譜圖中除了出現fve及其倍頻，還會出現其他低頻率的幅值；內溝道表面產生缺陷時，頻譜圖較為復雜，并且出現fvi。當溝道表面產生多個缺陷時，頻譜圖更加復雜。