蘋果采摘機器人末端執行器恒力柔順機構研制

苗玉彬，鄭家豐

蘋果采摘機器人末端執行器恒力柔順機構研制

苗玉彬，鄭家豐

（上海交通大學機械與動力工程學院，上海 200240）

為了減少采摘機器人末端執行器在夾持過程中對果實造成的損傷，該文通過在末端執行器上設置柔順機構，并對柔順機構力學性能進行計算，求解果實無損采摘所需的柔順恒力特性。首先，基于形狀函數建立邊界條件約束下的柔順梁非線性常微分控制方程；然后，利用打靶法將上述邊值問題重新描述為初值問題，并結合遺傳算法進行初值優化求解，采用序列二次規劃法優化梁的形狀函數，使其在一定變形范圍內實現恒力輸出；最后，在給出求解所需參數和柔順機構初始形狀參數基礎上，以蘋果采摘為例，通過優化計算，使柔順梁對果實的夾持力維持在7.9 N左右，非線性有限元計算和力-位移特性試驗驗證了計算結果的準確性，多次蘋果夾持試驗的抓取完好率為95%，驗證了該柔順機構無損夾持蘋果的可行性。研究結果可為不同類型果實的恒力夾持提供參考。

機器人；末端執行器；設計；恒力柔順機構；打靶法

0 引 言

采摘作業是果蔬生產中最耗時、費力的一個環節。隨著農業勞動力的減少，農業生產成本相應提高，果蔬采摘機器人逐漸成為農業機器人領域的研究熱點[1]。果實的無損采摘是采摘機器人的關鍵技術之一[2-7]，主要通過末端執行器和作物果實直接接觸。由于果實一般比較脆弱柔軟，形狀及生長狀況比較復雜，采摘過程中夾持力過大容易造成果實表面或內部損傷，而夾持力不足又無法抓牢果實。因此，合理地優化設計末端執行器，實現對果實的柔順抓取，是實現果實無損采摘的研究重點。

目前末端執行器無損夾持一般基于力的反饋控制實現，即利用壓力傳感器實時測量對果實的夾持力，將實際輸出與期望輸出對比構成閉環控制，使夾持力保持恒定。如王學林等[8]提出基于灰色預測的增量式比例積分力控制算法，根據預測模型的精度調整預測力偏差所占的權重，計算出穩定控制夾持力的校正量。周俊等[9]以當前抓取力和滑動信號小波變換的細節系數作為控制器的輸入，末端執行器閉合的距離作為控制器的輸出，采用混合學習算法結合減法聚類算法進行訓練，使抓取力超調量得到有效限制。Dimeas等[10]提出基于模糊控制的分層遞階控制策略，通過模糊控制器調節采摘草莓的抓取力。但由于受到成本和使用環境等因素限制，精確控制的末端執行器難以在農業領域得到廣泛應用[11]。

近年來，柔順機構引起廣泛關注。柔順機構是一種依靠機構中柔性構件的變形來完成全部運動，從而實現力或能量傳遞的機構[12-16]。柔性構件的應用使得在一定范圍內可以進行恒力輸出，減少恒力機構對力傳感和控制的需求。如張贏斌[17]研究了柔順鉗和柔順恒力機構設計的拓撲優化，采用相對密度法和非線性有限元方法對柔順鉗進行了優化設計。Merriam等[18]借助遺傳算法和有限元建模控制柔順伸縮器的結構參數，使其具有一定范圍內的恒力輸出。Wang等[19]用打靶法設計靜平衡機構和恒力機構，將它們串聯得到有穩定恒力輸出的恒力夾鉗，并使用有限元模型和實物模型驗證結果。Pham等[20]參考柔性雙穩態機構設計人字形柔順屈曲梁，通過非支配排序遺傳算法優化梁的形狀實現輸出力的調節。Liu等[21]采用傾斜的基于彎曲梁的柔性雙穩態機構來構造負剛度機構，設計了一種新型的柔性鉗，并采用非開關變結構控制算法克服滯后效應。

顯然，如果能利用恒力柔順機構對果蔬采摘機器人的末端采摘夾持器進行合理設計，在保持對果實可靠夾持的同時將夾持力控制在一定范圍，則既可以降低末端夾持裝置的復雜度，也能減少甚至避免對果實的夾持損傷。但現有的柔順恒力機構往往存在恒力區間相對機構尺寸小的缺陷，難以應用在果實采摘等要求結構設計緊湊的場合。為此，本文針對果實柔順夾持問題，在末端執行器的驅動機構和夾鉗之間設置柔順屈曲梁，并結合打靶法、遺傳算法計算求解柔順機構的數學模型，利用序列二次規劃法設計優化柔順機構的相關參數，使末端執行器在一定位移輸入范圍內具有恒力輸出特性，并可根據夾持力大小調整，從而實現對果實的恒力夾持。

1 柔順夾持機構設計與分析

1.1 采摘夾持器柔順設計

末端執行器按手爪個數可分為2指和多指型，用于蘋果等球狀果實的夾持器通常為弧形二指或三指結構[8,22-23]，夾持手指采用弧面結構以增大和果實的接觸面積、減少損傷。這種夾持器一般使用電動或氣動裝置驅動手指抓取果實，手指弧面上安裝有壓力傳感器獲取夾持力反饋，用以調節位移輸入。

以二指式末端執行器為例，圖1為二指式果實夾持末端執行器模型。當二指機構與果實接觸時，假定2指相對平行，則果實每側所受擠壓合力方向與該側機械手指的位移輸入方向相同，如圖1a所示。如果在驅動機構和弧面手指之間設置屈曲梁或類似柔順機構，當柔順機構的形狀滿足特定條件時，在一定位移輸入范圍內柔順機構變形，產生類似“超彈性”效果，使弧面手指保持恒力夾持，如圖1b所示。

注：Fin為輸入力，N；yin為位移輸入，cm；L1、L2分別為2段梁的長度，cm；t為柔順梁寬度，cm；w為柔順梁厚度，cm；n1、n2、n3為柔順梁節點，下同

由于結構的對稱性，取一側柔順機構進行計算，如圖1c所示。柔順機構由長為1和2的2段柔順梁組成，記為梁1和梁2，每段柔順梁均具有矩形橫截面，其中梁厚度為，寬度為以點1為坐標原點保持不動，點3處有豎直方向的位移量in。

圖2為柔順梁的大撓度變形模型，未變形的柔順梁由形狀函數()描述[24]，其中∈[0，1]，是沿中性軸的無量綱弧長，表示柔順梁相對軸的傾斜角度，rad。當受到外部負載時，偏轉梁由另一個函數()表示，rad。柔順梁受到的和方向的外力分別表示為F和F，N。中性軸上的任意點(,)表示為：

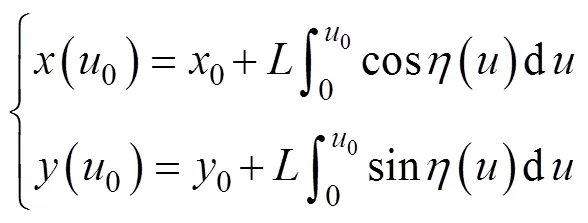
式中(0)，(0)表示無量綱弧長=0時的坐標，cm；為梁的長度，cm。

注：F和F分別為和方向的支反力，N；∈[0，1]，是沿中性軸的無量綱弧長；()表示未變形梁和軸的夾角，rad。()表示變形梁和軸的夾角，rad。

Note:FandFare reaction forces in theanddirections respectively, N;∈[0,1] is the dimensionless arc length along the neutral axis;() represents the angle between the undeformed beam and the-axis, rad；() represents the angle between the deformed beam and the-axis, rad.

圖2 柔順梁的大撓度非線性變形模型

Fig.2 Nonlinear large deformation model of compliant beam

將未變形梁的形狀函數利用多項式進行參數化處理，如式（2）所示。

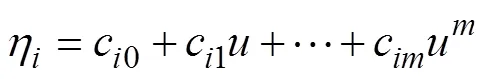
其中系數c0～c表征第段梁的形狀，將其描述為+1次多項式曲線。

根據文獻[25]，柔順梁的控制方程為：

式中為梁的抗彎剛度，其中是彈性模量，MPa；截面慣性矩=312，cm4；和分別等于F和F，N。

梁上的應力(MPa)如式（4）所示。

1.2 柔順梁變形模型的打靶法求解

以無量綱弧長為自變量，由式（1）、式（3）可得到控制梁變形的常微分方程組為：

式中下標=1，2分別表示圖1c中長度為1和2的2段梁。根據梁的力平衡、力矩平衡、轉角連續和幾何約束等條件，式（5）須滿足以下初始條件和邊界條件：

1）在點1處：

2）在點2處：

3）在點3處：

取梁形狀參數中=2，此時梁形狀曲線為三次多項式曲線，已能保證梁形狀的多樣性。當梁的控制參數10，11，12，20，21，22，1，2確定時，記未知初值1￠(0)為，整理得初值條件為

終值條件為

式（5）、（9）～（11）組成的非線性二階常微分方程組中含2個未知參數、和1個未知初值，其終值處有3個邊界條件，故可求解。本文采用打靶法[26]將邊值問題轉換為初值問題求解該微分方程組。為保證初值問題的求解精度，使用Matlab中的ode45函數[27]，即變步長的龍格庫塔法求解。將求解的結果終值與式（11）聯立得到三元非線性方程組。

該三元非線性方程組的求解需要給出適當的初值，否則容易陷入局部收斂。為此本文將此方程組的求解視作優化問題，首先使用具有全局優化能力的遺傳算法[28]得到一組可行解，并將該組解作為初值，代入到Matlab的fsolve函數，最終得到方程組的解。

方程組的解中等于y，為節點3在位移至in處時該點沿位移輸入方向的支反力。將求得的解代入初值問題過程量中，得到、、￠，進而得到位移輸入下柔順梁的形狀和梁上應力。柔順梁模型的求解過程如下：

1）給定梁優化的初值1、2、1、2。

2）通過ode45函數建立三元非線性方程組。

3）通過fsolve函數結合遺傳算法求解步驟2）中的非線性方程組得到未知參數、和未知初值。

4）將步驟3）中的解代入ode45函數數值求解每一步的函數值得到￠。

5）以￠建立1.3節中優化的目標和約束。

6）在優化過程中重復步驟1）～4），直至達到局部最優的1、2、1、2值，即最優柔順梁模型。

1.3 柔順梁模型優化

由式（1）～（2）可知，柔順梁模型的控制參數為10，11，12，20，21，22，1，2，為使一定位移輸入內的輸出力F保持恒定，使和這2個位移輸入下的輸出力盡量接近，定義函數()表示輸出力和位移輸入的關系，則柔順梁的優化模型可定義如下：

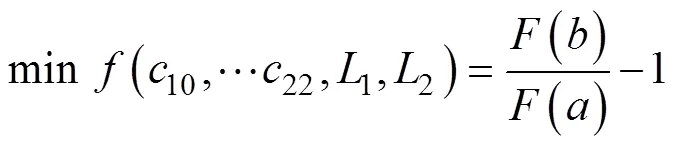
其中n1，n1，n3，n3分別為節點1和3的坐標，1，1，2，2分別為2段梁各點坐標，在梁模型求解步驟4）求得，cm。固定節點位置可以控制梁的設計邊界和坐標取值范圍，確保2段梁保持在一定邊界內，防止2段梁互相交叉。限制2段梁的長度1和2，可以防止梁發生自身交叉。上述變量的約束如圖1c中的虛線框所示，可根據柔順梁在末端執行器上的尺寸調整。位移輸入為時的應力c由式（4）求得，用于限制最大變形時梁的最大應力不超過許用應力，y是屈服應力，MPa。SF是安全系數。

式（13）為模型的約束條件，以保證優化后的柔順梁形狀能夠滿足末端執行器大小需求。梁模型優化為非線性最優化問題，采用序列二次規劃法（SQP，sequence quadratic program）[29]求解。但SQP為局部最優化算法，其初值的選取會影響最終優化結果，故此首先需要根據柔順機構特點定義梁的相對合理的初始形狀，再利用SQP算法進行優化。

2 柔順梁優化與試驗

2.1 柔順梁模型優化

采用前述優化算法對蘋果夾持末端執行器柔順梁模型進行優化和求解。根據柔順梁3D打印使用的聚甲醛材料和期望的恒力輸出區間，設定優化的相關參數為：彈性模量=2.6 GPa，屈服應力y=76 MPa，安全系數SF=1.5，=0.7 cm，=2 cm，最大允許應力下的位移輸入=2.2 cm，梁寬度=10 mm，梁厚度=1 mm。

優化后得到梁的形狀參數為：

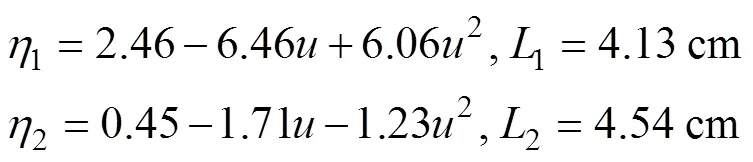
根據梁模型求解步驟4）得到優化后柔順梁的初始形狀和受到位移輸入作用后的變形形狀，如圖3所示。柔順梁的3個節點位置和2段梁的位置受優化模型中的約束條件限制，約束取值可按需求設置。柔順梁的最大應力出現在節點1處。柔順梁存在恒力輸出段的原因如下：由圖4中梁2的變形趨勢可見梁2在位移輸入方向上的剛度（抵抗變形的能力）隨位移輸入而減小，由正剛度結構變為負剛度結構。由梁1變形趨勢可見梁1始終為正剛度結構，梁1起到輔助梁2變形的作用。當2段梁在位移輸入方向上的剛度之和接近零剛度時，將存在一段輸出力不隨位移輸入發生變化的范圍。

圖3 柔順梁變形過程圖

圖4為優化前后柔順梁的力-位移曲線，其中()=3.911 6 N，()=3.960 5 N，并在最大位移處達到許用應力48.1 MPa。當夾持器夾取果實時，在0～位移范圍內夾持力持續增加，在～范圍內夾持力保持基本恒定，從而在不需要力反饋的條件下，實現了對果實的恒力柔順夾取。其恒力范圍可根據式（12）、式（13）進行調整。相比之下，優化前的柔順梁無“零剛度”段，夾持力隨位移輸入增大而明顯變化，無法實現恒力夾持。

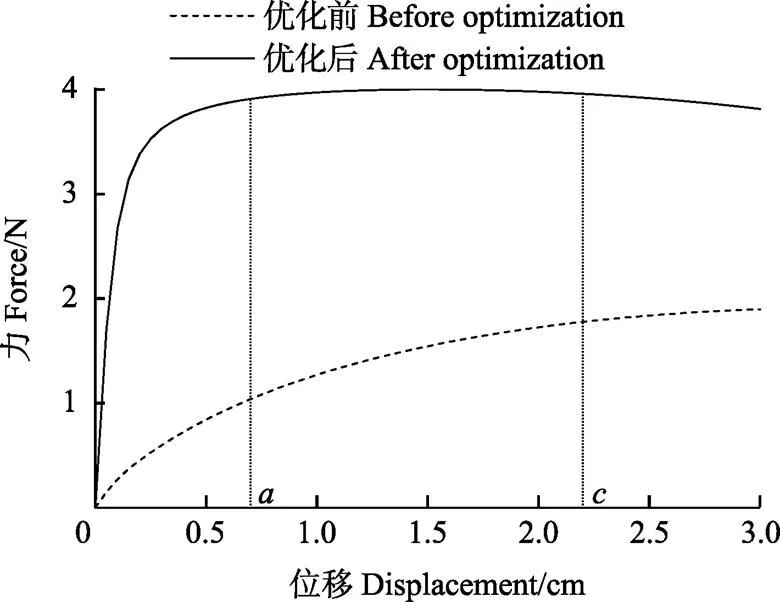
注：a～c表述優化時設定的恒力位移區間。

此外，由圖4中~恒力段數據，單側柔順梁對蘋果的夾持力約為3.95 N左右，夾持合力約為7.9 N，波動誤差不超過0.1 N。根據文獻[30]中的蘋果抓持試驗，以300 g蘋果為例，與夾持指摩擦系數為0.5時穩定抓取的力不小于3 N，當夾持力超過20 N（生物屈服力）后蘋果的內部組織將受到損傷，本文的優化結果滿足蘋果無損穩定采摘要求。當需要調整恒力大小時，不改變梁優化形狀即可實現，由式（3）知相同位移輸入下的支反力大小與抗彎剛度正相關。通過改變梁厚度或寬度可使梁具有不同的抗彎剛度，從而調整優化后柔順梁提供的恒力大小，使其適應不同種類果實的無損采摘需求。需要注意的是，梁厚度將影響梁受到的應力，當取較大值時，相同載荷下的應力增大，將限制柔順機構的操作范圍。

2.2 柔順梁力-位移特性仿真與試驗

為驗證本文方法的正確性，分別利用非線性有限元仿真和柔順梁力-位移特性試驗對上述結果進行對比驗證。為了加工方便和便于觀察試驗效果，對恒力結構進行了適當放大。實際使用時，一方面可結合連桿機構將柔順梁設置在合理位置而不是夾鉗上，另一方面可以將恒力結構的尺寸和恒力范圍縮小，通過機構并聯的方式實現期望的輸出特性，從而大大減小結構尺寸。

試驗裝置如圖5所示，柔順梁形狀參數與文中優化結果相同，使用聚甲醛材料通過3D打印加工而成，其彈性模量和屈服應力與優化時的材料參數設置一致。位移輸入裝置為步進電機驅動的線軌滑臺模組（盛斯達T6/4-200 mm，精度0.1 mm，水平最大負載2.5 kg）。裝置中柔順梁、絲桿導軌和數顯百分表（型號為BFQ-350A，量程50.8 mm、精度±0.02 mm）均固定，載物平臺在步進電機驅動下在絲桿導軌上移動并通過拉壓力傳感器（型號為JLBS-M2-3KG，量程3 kg，精度0.05%）對柔順梁施加位移輸入，力傳感器測量作用力數值，數顯百分表測量位移數值，力與位移一一對應得到力-位移曲線。

1. 數字百分表 2. 絲杠導軌 3. 載物平臺 4. 力傳感器 5. 柔順梁

非線性有限元仿真在有限元分析軟件Abaqus中進行，以柔順梁優化結果的形狀建立梁單元模型，設定彈性模量為2.6 GPa（與優化參數相同），邊界條件如圖1c所示（1固支，3設置位移輸入且限制其他方向自由度），并劃分為866個網格單元，記錄3位移輸入和1相應的支反力。

圖6為Abaqus仿真結果中位移輸入為2.2 cm時梁的應力云圖，其中最大應力47.87 MPa，與本文算法的實際計算結果48.10 MPa誤差為-0.48%。Abaqus對梁的力-位移關系對比驗證結果如圖7所示，位移輸入范圍0.2～2.8 cm，間隔0.2 cm，共14個點。仿真結果與計算相比，支反力平均誤差為-0.007 N，平均相對誤差-0.18%，最大誤差為-0.038N，最大相對誤差-0.96%，計算結果精度較高，表明本文梁模型的計算方法理論可行。

測試試驗的位移輸入范圍0.2～2 cm，間隔0.05 cm，共37個測點。與本文模型計算結果相比，試驗測得的支反力平均誤差為0.198 N，平均相對誤差5.06%，最大誤差為0.215 N，最大相對誤差5.8%。試驗結果與計算結果大致吻合，說明本文梁模型實際可實現。圖中試驗結果比計算、仿真值稍大，而仿真結果、計算結果吻合，其主要原因是仿真分析和計算的理論模型只考慮了中性軸的變形，而實際中存在梁厚度，使得連接處的剛性比理論模型稍大，同時也存在打印加工誤差和材料彈性模量誤差，使試驗結果相對理論分析值產生偏差。

圖6 位移輸入為2.2 cm時柔順梁應力云圖

圖7 力-位移特性驗證結果

2.3 蘋果抓取試驗

采用文中機構對蘋果進行柔順夾持，夾持試驗裝置如圖8所示，力傳感器與驗證試驗相同。夾持指Ⅰ固定不動，夾持指Ⅱ通過力傳感器安裝在載物平臺上。在步進電機驅動下，載物平臺在絲桿導軌上移動，帶動夾持指Ⅱ與夾持指Ⅰ合攏夾緊蘋果，載荷大小由力傳感器讀取。

以1次抓取試驗為例，圖9為抓取蘋果時柔順梁夾持力隨時間變化曲線，將載荷開始增大的時間記為0時刻。從夾持指Ⅰ開始接觸蘋果時載荷開始迅速增大，當夾持力大約達到8 N時進入柔順梁的恒力范圍；隨時間增加，步進電機繼續驅動夾持指夾緊，夾持力基本穩定。取夾持力穩定段4～7 s共150個數據點進行分析，得到支反力波動范圍為7.46～8.42 N，平均支反力為8.03 N，與模型計算值的誤差為1.6%，與力-位移驗證試驗結果的誤差為-0.84%。由此可見，實際蘋果夾持時雖然夾持力有一定波動，但夾持恒力與計算結果基本相符。

1. 絲杠導軌 2. 載物平臺 3. 力傳感器 4. 夾持指Ⅱ 5. 夾持指Ⅰ

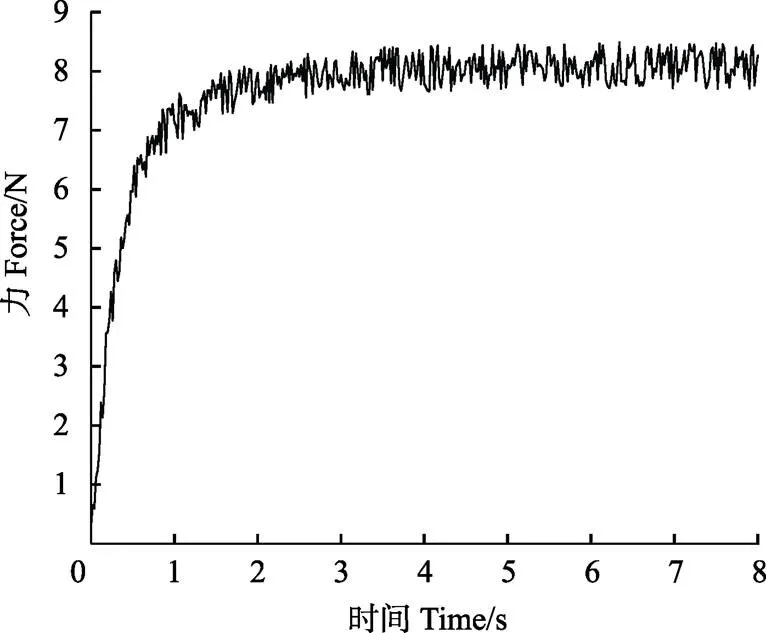
圖9 蘋果抓取試驗夾持力

為進一步驗證夾持機構的柔順性，選取大小相近、表面完好的20個蘋果進行抓取試驗，夾持持續時間為 10 s，均沒有發生滑落現象。將蘋果靜置24 h，人工觀察蘋果表皮只有1個蘋果表面出現壞點抓取完好率為95%。由于夾持力未達到蘋果的生物屈服力，該蘋果內部未發生損傷，其表面損傷的原因可能是由于表面與夾持指不貼合，導致局部壓強較大。

3 結 論

1）針對果蔬采摘機器人無損采摘需求，通過在末端執行器上設置柔順機構，并對柔順機構的力學性能進行優化計算，獲取果實無損采摘所需的柔順恒力特性。

2）建立柔順梁的變形控制微分方程組，采用打靶法將邊值問題重新描述為初值問題，并結合遺傳算法優化求解初值。在此基礎上，采用序列二次規劃法優化計算梁的形狀函數，使柔順梁對蘋果的恒定夾持力維持在7.9 N左右。

3）分別進行非線性有限元仿真和柔順梁力-位移特性試驗，仿真與模型計算結果相符，試驗與模型計算結果平均誤差為5.06%。進行蘋果抓取試驗，夾持力波動為7.46～8.42 N，平均恒定夾持力約為8.03 N，滿足蘋果無損夾持需求。

4）多次蘋果夾持試驗的抓取完好率為95%，驗證了該柔順機構無損夾持蘋果的可行性。通過適當調整柔順梁的參數，本文算法可適應不同類型果實的恒力夾持需求，可為柔順機構在果蔬無損夾持采摘中的有效應用提供參考。

[1] 宋健，張鐵中，徐麗明，等. 果蔬采摘機器人研究進展與展望[J]. 農業機械學報，2006，37(5)：158－162. Song Jian, Zhang Tiezhong, Xu Liming, et al. Research actuality and prospect of picking robot for fruits and vegetables[J]. Transactions of the Chinese Society for Agricultural Machinery, 2006, 37(5): 158－162. (in Chinese with English abstract)

[2] Liu F, Ji W, Tang W, et al. Research on grasping planning for apple picking robot’s end-effector[C]//Proceedings of the 2015 Chinese Intelligent Systems Conference. Berlin Heidelberg: Springer, 2016: 95－103.

[3] Bac C W, Hemming J, Van Tuijl J, et al. Performance evaluation of a harvesting robot for sweet pepper[J]. Journal of Field Robotics, 2017, 34(6): 1123－1139.

[4] 徐麗明，劉旭東，張凱良，等. 臍橙采摘機器人末端執行器設計與試驗[J]. 農業工程學報，2018，34(12)：53－61. Xu Liming, Liu Xudong, Zhang Kailiang, et al. Design and test of end-effector for navel orange picking robot [J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(12): 53－61. (in Chinese with English abstract)

[5] 傅隆生，張發年，槐島芳德，等. 獼猴桃采摘機器人末端執行器設計與試驗[J]. 農業機械學報，2015，46(3)：1－8. Fu Longsheng, Zhang Fanian, Yoshinori G, et al. Development and experiment of end-effector for kiwifruit harvesting robot[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(3): 1－8. (in Chinese with English abstract)

[6] Chiu Y C, Yang P Y, Chen S. Development of the end-effector of a picking robot for greenhouse-grown tomatoes[J]. Applied Engineering in Agriculture, 2013, 29(6): 1001－1009.

[7] Kondo N, Yamamoto K, Shimizu H, et al. A machine vision system for tomato cluster harvesting robot[J]. Engineering in Agriculture Environment & Food, 2009, 2(2): 60－65.

[8] 王學林，姬長英，周俊，等. 基于灰色預測控制的果蔬抓取系統設計與試驗[J]. 農業工程學報，2010，26(3)：112－117. Wang Xuelin, Ji Changying, Zhou Jun, et al. Design and experiment of fruit and vegetable grasping system based on grey prediction control[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(3): 112－117. (in Chinese with English abstract)

[9] 周俊，楊肖蓉，朱樹平. 基于自適應神經模糊網絡的果蔬抓取力控制[J]. 農業機械學報，2014，45(7)：67－72. Zhou Jun, Yang Xiaorong, Zhu Shuping. Fruit and vegetable grasping force control based on adaptive neural fuzzy network[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(7): 67－72. (in Chinese with English abstract)

[10] Dimeas F, Sako D V. Design and fuzzy control of a robotic gripper for efficient strawberry harvesting[J]. Robotica, 2015, 33(5): 1085－1098.

[11] 章軍. 六關節三指蘋果抓取機械手的自適應柔性分析[J]. 農業工程學報，2010，26（1）：140－144. Zhang Jun. Analysis of adaptive flexibility of three-finger manipulator with six-joint for grasping apple[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(1): 140－144. (in Chinese with English abstract)

[12] Ling M , Cao J , Jiang Z , et al. Development of a multistage compliant mechanism with new boundary constraint[J]. Review of Scientific Instruments, 2018, 89(1): 015009.

[13] Zhang X, Zhu B. Topology optimization of compliant mechanisms[M]. Singapore: Springer Singapore. 2018.

[14] Li Y, Chen Y, Yang Y, et al. Passive particle jamming and its stiffening of soft robotic grippers[J]. IEEE Transactions on Robotics, 2017, 33(2): 446－455.

[15] 張愛梅. 平面梁大撓度非線性問題的完備解與柔順機構精確建模[D]. 西安：西安電子科技大學，2013. Zhang Aimei. Comprehensive Solution to Nonlinear Large-Deflection Problems of Planar Beams and Accurate Modeling of Compliant Mechanisms[D]. Xi’an: Xidian University, 2013. (in Chinese with English abstract)

[16] 李庚. 空間大撓度梁的變形計算及其在空間柔順機構建模中的應用[D]. 西安：西安電子科技大學，2016. LI Geng. Deformation Calculation of Spatial Large Deflection Beam and its Application on the Modeling of Spatial Compliant Mechanisms[D]. Xi’an: Xidian University, 2016. (in Chinese with English abstract)

[17] 張贏斌. 拓撲優化法設計柔順恒力機構[D]. 西安：西安電子科技大學，2012. Zhang Yingbin. Design Compliant Constant Force Mechanism Using Topology Optimization[D]. Xi’an: Xidian University, 2012. (in Chinese with English abstract)

[18] Merriam E G, Colton M B, Magleby S, et al. The design of a fully compliant statically balanced mechanism[C]//ASME 2013 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference. 2013, 6A(7): doi: 10.1115/DETC2013-13142

[19] Wang J Y, Lan C C. A constant-force compliant gripper for handling objects of various sizes[J]. Journal of Mechanical Design, 2014, 136(7): doi: 10.1115/1.4027285

[20] Pham H T, Wang D A. A constant-force bistable mechanism for force regulation and overload protection[J]. Mechanism & Machine Theory, 2011, 46(7): 899－909.

[21] Liu Y, Zhang Y, Xu Q. Design and control of a novel compliant constant-force gripper based on buckled fixed-guided beams[J]. IEEE/ASME Transactions on Mechatronics, 2016, 22(1): 476－486.

[22] 姬偉，李俊樂，楊俊，等. 機器手采摘蘋果抓取損傷機 理有限元分析及驗證[J]. 農業工程學報，2015，31(5)： 17－22. Ji Wei, Li Junle, Yang Jun, et al. Analysis and validation for mechanical damage of apple by gripper in harvesting robot based on finite element method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(5): 17－22. (in Chinese with English abstract)

[23] 姬偉，羅大偉，李俊樂，等. 果蔬采摘機器人末端執行器的柔順抓取力控制[J]. 農業工程學報，2014，30(9)：19－26. Ji Wei, Luo Dawei, Li Junle, et al. Compliance grasp force control for end-effector of fruit-vegetable picking robot[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(9): 19－26. (in Chinese with English abstract)

[24] Lan C C, Wang J H, Chen Y H. A compliant constant-force mechanism for adaptive robot end-effector operations[C]// Proceedings of the IEEE International Conference on Robotics and Automation. IEEE, 2010: 2131－2136.

[25] Lan C C, Cheng Y J. Distributed shape optimization of compliant mechanisms using intrinsic functions[J]. Journal of

Mechanical Design, 2008, 130(7): 3－11.

[26] Yin X, Lee K M, Lan C C. Computational models for predicting the deflected shape of a non-uniform, flexible finger[C]//Proceeedings of the IEEE International Conference on Robotics and Automation. IEEE, 2004: 2963－2968.

[27] 薛定宇，陳陽泉. 高等應用數學問題的MATLAB求解[M]. 北京：清華大學出版社，2004.

[28] John H. Mathews, Kurtis D Fink. 數值方法（MATLAB版）[M]. 北京：電子工業出版社，2005.

[29] 馬昌鳳. 最優化方法及其Matlab程序設計[M]. 北京：科學出版社，2010.

[30] 唐偉. 蘋果采摘機器人末端執行器無損主動抓取技術研究[D]. 鎮江：江蘇大學，2017. Tang Wei. Research on Non-destructive and Active Grasp Technology for End-Effector of Apple Picking Robot[D]. Zhenjiang: Jiangsu University, 2017. (in Chinese with English abstract)

Development of compliant constant-force mechanism for end effector of apple picking robot

Miao Yubin, Zheng Jiafeng

(,,200240,)

In order to reduce the damage caused by end effector of picking robot during fruit clamping process, non-destructive fruit picking has gradually become a key technology of fruit harvesters. The application of compliant constant-force mechanism may enable a constant output force within a certain range of operating displacement. The existing compliant constant force mechanism has the defect that the constant force interval is small relative to the size of the mechanism, which makes it difficult to apply in the situations requiring compact structure design such as fruit picking. In this paper, a method to generate compliant constant-force mechanism is introduced. Firstly, based on the shape function, a set of nonlinear ordinary differential equations for buckling deformation of compliant beams under boundary conditions is established. Secondly, the boundary value problem is redescribed as the initial value problem by applying the shooting method combined with the Runge-kutta method, the 3D nonlinear equations are obtained according to three boundary conditions, two unknown variables and one unknown initial value. Thirdly, the nonlinear equations is solved as an optimization problem. To avoid the optimization problem falling into local convergence, the genetic algorithm is employed to globally find the appropriate initial values of the three unknowns in the nonlinear equations, the solution of the differential equations is obtained according to the principle of the shooting method. Finally, the sequential quadratic programming method is implemented to optimize the parameters of the shape function, the optimization objective is to achieve a constant output force within a certain range of displacement input, and the constraints are the design boundary and the maximum permissible stress of the beams. A two-finger apple picking end effector is taken as an example, the initial shape parameters of the compliant mechanism are set and the algorithm is realized in Matlab. After optimization, the constant clamping force of the compliant beam to the fruit is about 7.9 N. In order to verify the correctness of the method, the non-linear finite element simulation is carried out in Abaqus, and the force-displacement experiment is carried out. The simulation results agree well with calculations, compared to the calculations, the average error of force-displacement test is 5.06%, which is acceptable. The main reason for the error may be that the theoretical model only considers the deformation of the neutral axis. The apple picking test is designed to verify the practicality of the method. At constant-force range, the clamping force fluctuates from 7.46-8.42 N, and the average clamping force is about 8.03 N. The clamping force is basically consistent with the calculation results though a certain fluctuation exists. To further verify the flexibility of the clamping mechanism, 20 apples of similar size and intact surface are selected for clamping test. The result shows that the ratio of non-destructive grasping is 95%, no slipping occurred, the compliant mechanism designed can achieve stable clamping of apples. The algorithm can meet the requirements of constant force clamping for different types fruit by properly adjusting the parameters of the compliant beam. The research provides a reference for the effective application of the compliant mechanism in non-destructive fruit-picking.

robots; end effectors; design; compliant constant force mechanism; shooting method

10.11975/j.issn.1002-6819.2019.10.003

TP241

A

1002-6819(2019)-10-0019-07

2018-12-12

2019-01-15

上海市科研計劃項目（16391901700）；滬農科推字（2018）第1-2號、（2015）第4-1號；上海市工程技術研究中心建設專項（17DZ2252300）

苗玉彬，副教授，主要從事智能裝備、智能傳感器研究。Email：ybmiao@sjtu.edu.cn

苗玉彬，鄭家豐.蘋果采摘機器人末端執行器恒力柔順機構研制[J]. 農業工程學報，2019，35(10)：19－25. doi：10.11975/j.issn.1002-6819.2019.10.003 http://www.tcsae.org

Miao Yubin, Zheng Jiafeng. Development of compliant constant-force mechanism for end effector of apple picking robot[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(10): 19－25. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.10.003 http://www.tcsae.org