404 Not Found
404 Not Found
立足忘“形”得“一” 實(shí)現(xiàn)由“厚”到“薄”*
●劉鑫鈞 高 嬌
(灌南高級(jí)中學(xué),江蘇 灌南 222500)
道生一,一生二,二生三,三生萬(wàn)物.學(xué)習(xí)的關(guān)鍵在于領(lǐng)悟“道”,而要領(lǐng)悟“道”就需先得“一”,這個(gè)“一”應(yīng)該是簡(jiǎn)單的、也是最本質(zhì)的.然而在高三復(fù)習(xí)教學(xué)中,學(xué)生往往被厚厚的書(shū)本、沉甸甸的試卷壓得喘不過(guò)氣來(lái),教師不斷重復(fù)、拉網(wǎng)式的講題,只見(jiàn)厚的教學(xué),卻未見(jiàn)教學(xué)的薄,使得學(xué)生只見(jiàn)“萬(wàn)物”而未得一.
如何得“一”呢?這就需要忘“形”.而這之前需要經(jīng)歷3個(gè)過(guò)程,即展“形”、變“形”與析“形”,通過(guò)這3個(gè)過(guò)程對(duì)相關(guān)聯(lián)的或類(lèi)似的概念、問(wèn)題、認(rèn)識(shí)等作橫向、縱向溝通,并力求在“越界而讀”上下足功夫,即將所學(xué)知識(shí)讀厚,接下來(lái)需要的就是讀薄,忘卻“外在的形”(即非本質(zhì)的屬性),只有這樣心中才一片空明,才能吐故納新、忘卻形式、抽象本質(zhì),乃為得其“一”.本文基于筆者的教學(xué)經(jīng)驗(yàn),從3個(gè)方面來(lái)闡述在高三復(fù)習(xí)教學(xué)中如何忘“形”得“一”,實(shí)現(xiàn)教學(xué)的“厚”向教學(xué)的“薄”轉(zhuǎn)化.
1 忘“形”得“一”,領(lǐng)悟概念之間的聯(lián)系性
概念復(fù)習(xí)教學(xué)的一個(gè)重點(diǎn)就是讓學(xué)生認(rèn)識(shí)到概念之間具有一定的聯(lián)系,而不是割裂地認(rèn)識(shí)問(wèn)題.在概念復(fù)習(xí)教學(xué)中,如何提高概念知識(shí)的聯(lián)系性呢?
1.1 展“形”——呈現(xiàn)概念的形式化語(yǔ)言
案例1 “函數(shù)單調(diào)性”概念的復(fù)習(xí)教學(xué).
符號(hào)語(yǔ)言的抽象性使得學(xué)生對(duì)概念理解存在一定的困難,因此,在復(fù)習(xí)教學(xué)時(shí)需要加強(qiáng)學(xué)生對(duì)概念形式化定義的進(jìn)一步理解,以函數(shù)單調(diào)性概念為例,在高三復(fù)習(xí)時(shí)可以讓學(xué)生回顧、表述概念的形式化定義.
問(wèn)題1 什么是單調(diào)遞增函數(shù)?它是如何定義的?
生:一般地,設(shè)函數(shù)y=f(x)的定義域?yàn)锳,區(qū)間I?A.如果對(duì)于區(qū)間I內(nèi)的任意兩個(gè)值x1,x2,當(dāng)x1 教師可以向?qū)W生依次提出以下4個(gè)問(wèn)題,通過(guò)不斷變化定義的形式,讓學(xué)生真正感悟概念形式化定義的本質(zhì). 問(wèn)題2 把“f(x1) 問(wèn)題3 把“f(x1) 上面這些形式各有不同,如何把握它們的聯(lián)系與區(qū)別,將學(xué)生對(duì)概念的本質(zhì)認(rèn)識(shí)不斷引向深處呢?可以向?qū)W生追問(wèn)以下5個(gè)問(wèn)題. 問(wèn)題6 單調(diào)性實(shí)質(zhì)上就是考查f(x2)-f(x1)與x2-x1之間的什么關(guān)系? 問(wèn)題7 (x2-x1)[f(x2)-f(x1)]>0;當(dāng)x1 問(wèn)題9 若A(x1,f(x1)),B(x2,f(x2))為函數(shù)y=f(x)圖像上的兩個(gè)點(diǎn),那么函數(shù)f(x)在[x1,x2]上的平均變化率是什么?與單調(diào)性有什么關(guān)系? 問(wèn)題10 “函數(shù)在區(qū)間A上的單調(diào)性”與其導(dǎo)數(shù)f′(x)有何關(guān)系呢? 高三解題教學(xué)貴在跳出題海,掌握基本的解題經(jīng)驗(yàn),使學(xué)生獲得一類(lèi)試題的通法通性,不被試題“外在之形”所迷惑,于四面題海之中獲“試題之本意”,從紛繁復(fù)雜之中跳出來(lái),游刃而有余.那么,在解題教學(xué)中如何忘“形”得“一”,才能讓學(xué)生掌握一類(lèi)試題的普適性解法呢? 案例2 直線(xiàn)與圓的一類(lèi)比例問(wèn)題的解題教學(xué). 《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)(2017年版)》強(qiáng)調(diào):對(duì)學(xué)生“直觀想象”這一數(shù)學(xué)核心素養(yǎng)的培養(yǎng),指借助幾何直觀和空間想象感知事物的形態(tài)與變化,利用空間形式特別是圖形,培養(yǎng)理解和解決數(shù)學(xué)問(wèn)題的素養(yǎng).因此,在解題教學(xué)中要鼓勵(lì)學(xué)生把試題中元素的位置、形態(tài)用圖形語(yǔ)言表示出來(lái).從哪入手呢?波利亞指出:從最簡(jiǎn)單的開(kāi)始. 例1 過(guò)點(diǎn)P(-4,0)的直線(xiàn)l與⊙C:(x-1)2+y2=5相交于點(diǎn)A,B,若點(diǎn)A恰好是線(xiàn)段PB的中點(diǎn),則直線(xiàn)l的方程為_(kāi)_____. 圖1 該題的圖形表征大致如圖1所示.在表征的過(guò)程中認(rèn)識(shí)到:只有當(dāng)直線(xiàn)l處于一個(gè)特定位置時(shí),點(diǎn)A才可能恰好是線(xiàn)段PB的中點(diǎn).在畫(huà)圖的過(guò)程中,發(fā)現(xiàn)學(xué)生畫(huà)圖的順序有所不同,有的學(xué)生是先畫(huà)直線(xiàn),后標(biāo)注點(diǎn)A,B,即先產(chǎn)生直線(xiàn),因此可以先假設(shè)直線(xiàn)斜率k,然后求點(diǎn);有的學(xué)生先畫(huà)點(diǎn),再聯(lián)結(jié)兩點(diǎn)所在直線(xiàn),最后出現(xiàn)另一點(diǎn),這樣就可以設(shè)點(diǎn)來(lái)做.利用幾何圖形描述問(wèn)題,借助幾何直觀理解問(wèn)題,在圖形表征過(guò)程中實(shí)現(xiàn)了動(dòng)態(tài)地理解問(wèn)題. 解題教學(xué)不僅要一題多解,更要善于多題一解,因此要善于對(duì)問(wèn)題進(jìn)行變式.顧泠沅等學(xué)者把變式教學(xué)分為概念性變式教學(xué)和過(guò)程性變式教學(xué)兩類(lèi).概念性變式教學(xué)突出對(duì)概念內(nèi)涵的理解,過(guò)程性變式教學(xué)突出對(duì)概念外延的應(yīng)用,注重知識(shí)之間的聯(lián)系和拓展,通過(guò)過(guò)程性變式教學(xué),使數(shù)學(xué)教學(xué)有層次地遞進(jìn)[1].利用過(guò)程性變式可以對(duì)一個(gè)初始問(wèn)題進(jìn)行變式,從而深化對(duì)這類(lèi)問(wèn)題的認(rèn)識(shí). 2.2.1 改變?cè)?/p> 變式1 (定點(diǎn)變動(dòng)點(diǎn))過(guò)點(diǎn)E(2,t)作直線(xiàn)l與⊙C:x2+y2=1交于點(diǎn)M,N,若點(diǎn)M恰好是線(xiàn)段NE的中點(diǎn),則實(shí)數(shù)t的取值范圍是______. 變式2 (豎線(xiàn)變斜線(xiàn))已知⊙C:(x-2)2+y2=1,點(diǎn)P在直線(xiàn)l:x+y+1=0上,若過(guò)點(diǎn)P存在直線(xiàn)m與⊙C交于點(diǎn)A,B,且點(diǎn)A為PB的中點(diǎn),則點(diǎn)P橫坐標(biāo)x0的取值范圍是______. 變式3 (定圓變動(dòng)圓)已知△ABC的3個(gè)頂點(diǎn)A(-1,0),B(1,0),C(3,2),其外接圓為⊙H. 1)略. 2)對(duì)于線(xiàn)段BH上的任意一點(diǎn)P,若在以C為圓心的圓上都存在兩個(gè)不同的點(diǎn)M,N,使得點(diǎn)M是線(xiàn)段PN的中點(diǎn),求⊙C的半徑r的取值范圍. 圖2 2.2.2 變更條件 變式4 (中點(diǎn)變向量)如圖2,在平面直角坐標(biāo)系xOy中,已知⊙M:x2+y2-12x-14y+60=0及其上一點(diǎn)A(2,4). 1),2)略. 變式5 (直線(xiàn)變動(dòng)圓,中點(diǎn)變比例)在平面直角坐標(biāo)系xOy中,⊙C1:(x+1)2+(y-6)2=25,⊙C2:(x-17)2+(y-30)2=r2.若⊙C2上存在一點(diǎn)P,使得過(guò)點(diǎn)P可作一條射線(xiàn)與⊙C1依次交于點(diǎn)A,B,滿(mǎn)足PA=2AB,則半徑r的取值范圍是______. 圖3 例1及5個(gè)變式的圖形表征如圖3所示,下面需要整合這6個(gè)圖形,即把一些零散的東西通過(guò)某種方式而彼此銜接,其主要的精髓在于將零散的要素組合在一起,并最終形成有價(jià)值、有效率的整體. 首先,可以看出從例1到變式1是定點(diǎn)變動(dòng)點(diǎn),變式2中的直線(xiàn)可以是橫線(xiàn)(x軸)、豎線(xiàn)或斜線(xiàn),其中線(xiàn)段比例關(guān)系為1∶1,圓始終是定圓.因此,這3個(gè)圖形可以整合為下列一個(gè)基本的模型. 模型1 過(guò)直線(xiàn)l上一點(diǎn)P作一條直線(xiàn),交定圓于點(diǎn)A,B,其中PA∶AB=1∶1. 在高三的解題教學(xué)之中,如果就題講題,那么教師、學(xué)生都將陷于題海之中而不能自拔,如何得其“一”,而忘其形呢?關(guān)鍵的一步就是要對(duì)題型、解法歸一. 2.4.1 題型的概括抽象 2.4.2 解法的提煉與統(tǒng)一 通過(guò)以上分析發(fā)現(xiàn)這6道題本質(zhì)上是一類(lèi)題型,因此,在教學(xué)的過(guò)程中應(yīng)引導(dǎo)學(xué)生掌握這一類(lèi)題型普適性的解法,而不是一題一題進(jìn)行講解.為便于具體說(shuō)明,這里以曲線(xiàn)C是直線(xiàn)或圓、C1是⊙H:(x-a)2+(y-b)2=r2為例. 利用點(diǎn)B在⊙H上,得方程 整理變形,得 (1) 然后利用點(diǎn)A在⊙H上,獲得方程 (x1-a)2+(y1-b)2=r2. (2) 數(shù)學(xué)教學(xué)重在培養(yǎng)學(xué)生的思維,而思維的水平又有高低之分.在高中數(shù)學(xué)課堂教學(xué)中,要善于引導(dǎo)學(xué)生對(duì)問(wèn)題進(jìn)行深刻理解.深刻性指思維活動(dòng)的抽象性和邏輯推理水平,表現(xiàn)為能深刻分析、理解問(wèn)題,善于抓住事物的本質(zhì)和規(guī)律.具體表現(xiàn)在3個(gè)維度:寬度、深度和完整度.那么,在解題教學(xué)中如何忘“形”得“一”,才能讓學(xué)生對(duì)問(wèn)題有深刻性的理解呢? 案例3 運(yùn)用韋達(dá)定理求直線(xiàn)與橢圓交點(diǎn)坐標(biāo). 直線(xiàn)與橢圓的位置關(guān)系有3類(lèi):相離、相切、相交.當(dāng)直線(xiàn)與橢圓相交時(shí),如何求直線(xiàn)與橢圓的交點(diǎn)坐標(biāo)呢?理論上直接聯(lián)立直線(xiàn)方程與橢圓方程,得方程組 消去x(或y)得到關(guān)于y(或x)的方程,解這個(gè)方程即可.如果知道一個(gè)交點(diǎn)的坐標(biāo),利用韋達(dá)定理和或積的形式會(huì)更加簡(jiǎn)便,因此,運(yùn)用韋達(dá)定理求直線(xiàn)與橢圓的交點(diǎn)問(wèn)題主要是針對(duì)直線(xiàn)與橢圓相交、且已知其中一點(diǎn)坐標(biāo)這一類(lèi)模型.用圖形表征如圖4所示. 圖4 圖5 2)若x0=0,求橢圓的離心率; (2015年江蘇省南通市第二次模擬試題第18題) 分析 由于點(diǎn)P(x0,y0)滿(mǎn)足PA⊥PF,從而 化簡(jiǎn),得 (3) 因?yàn)辄c(diǎn)P(x0,y0)在橢圓上,所以 (4) 聯(lián)立式(3)和式(4),得 (5) 于是 因此 圖6 圖7 分析 例3中求點(diǎn)P的橫坐標(biāo)與例2的解法是一致的,同樣可得到關(guān)于xP的一個(gè)一元二次方程,然后要看出a是方程的根.利用韋達(dá)定理求出xP,最后利用xP∈(-a,a)求出離心率的范圍. 通過(guò)對(duì)圖5和圖6分析發(fā)現(xiàn),韋達(dá)定理適用于這樣一類(lèi)模型,這一類(lèi)模型具有更一般的特征:如果動(dòng)點(diǎn)P與定點(diǎn)A(a,b)在橢圓上,Q(m,0),其中m為常數(shù),且PA⊥QA,如圖7所示. 圖8 1)求橢圓C的方程. 2)是否存在常數(shù)λ,使得k1=λk恒成立?若存在,求出λ的值;若不存在,請(qǐng)說(shuō)明理由. 2)判斷常數(shù)λ是否存在的關(guān)鍵是求出k1,k2,因此問(wèn)題的關(guān)鍵在于如何求解k1(求解k2同理可得),即點(diǎn)A1,B1的坐標(biāo)如何求解,但點(diǎn)A1,B1都是動(dòng)點(diǎn),不屬于前兩類(lèi)模型,怎么辦?受圖4的啟發(fā),可以先設(shè)A(x0,y0),暫時(shí)把x0看成常數(shù),首先求出直線(xiàn)AM的方程 因?yàn)樵摲匠逃袃蓚€(gè)根x0,xA1,所以 化簡(jiǎn)得 則 同理可得 下略. 對(duì)圖4~8進(jìn)行分析可知:運(yùn)用韋達(dá)定理求直線(xiàn)與橢圓交點(diǎn)具有廣泛性,其中圖7所代表的題型是對(duì)圖5與圖6所代表的題型的一般性概括.這些圖形大致可以分為3類(lèi):第一類(lèi)如圖4所示,過(guò)橢圓上一定點(diǎn)作直線(xiàn)l交橢圓于另一點(diǎn),求另一點(diǎn)坐標(biāo);第二類(lèi)如圖7所示,已知橢圓上動(dòng)點(diǎn)P與定點(diǎn)A(a,b),定點(diǎn)Q(m,0)不在橢圓上,且PA⊥QA,求動(dòng)點(diǎn)P坐標(biāo);第三類(lèi)如圖8所示,已知橢圓上雙動(dòng)點(diǎn),求動(dòng)點(diǎn)坐標(biāo). 通過(guò)前面的展“形”、變“形”、析“形”,對(duì)運(yùn)用韋達(dá)定理求直線(xiàn)交點(diǎn)這一問(wèn)題有比較深入的認(rèn)識(shí).試題的形式千變?nèi)f化,因此需忘卻形式,獲得本質(zhì)的認(rèn)識(shí),才能靈活地運(yùn)用韋達(dá)定理去解題.雖然形式上有3類(lèi)題型,但是本質(zhì)上就一種,就是最后獲得關(guān)于坐標(biāo)的一元二次方程 (6) 展“形”只是第一境界:見(jiàn)山是山,見(jiàn)招是招.變“形”是第二境界:見(jiàn)山不是山,見(jiàn)招不是招,學(xué)生經(jīng)過(guò)展“形”、變“形”,即不斷讀厚的過(guò)程,之后會(huì)發(fā)現(xiàn),到處都是山到處都是招.下面就需要一個(gè)讀薄的過(guò)程,這就需要析“形”與忘“形”,忘就是為了記,忘卻形式,記住本質(zhì),方能得“一”.最后進(jìn)入學(xué)習(xí)的第三境界:見(jiàn)畫(huà)還是畫(huà),見(jiàn)招還是招,道法自然,一切從心.1.2 變“形”——基于問(wèn)題串追問(wèn)概念的形式化語(yǔ)言


1.3 析“形”——探究不同形式語(yǔ)言的區(qū)別與聯(lián)系

1.4 得“一”——概括形式語(yǔ)言的本質(zhì)與聯(lián)系
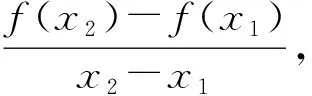
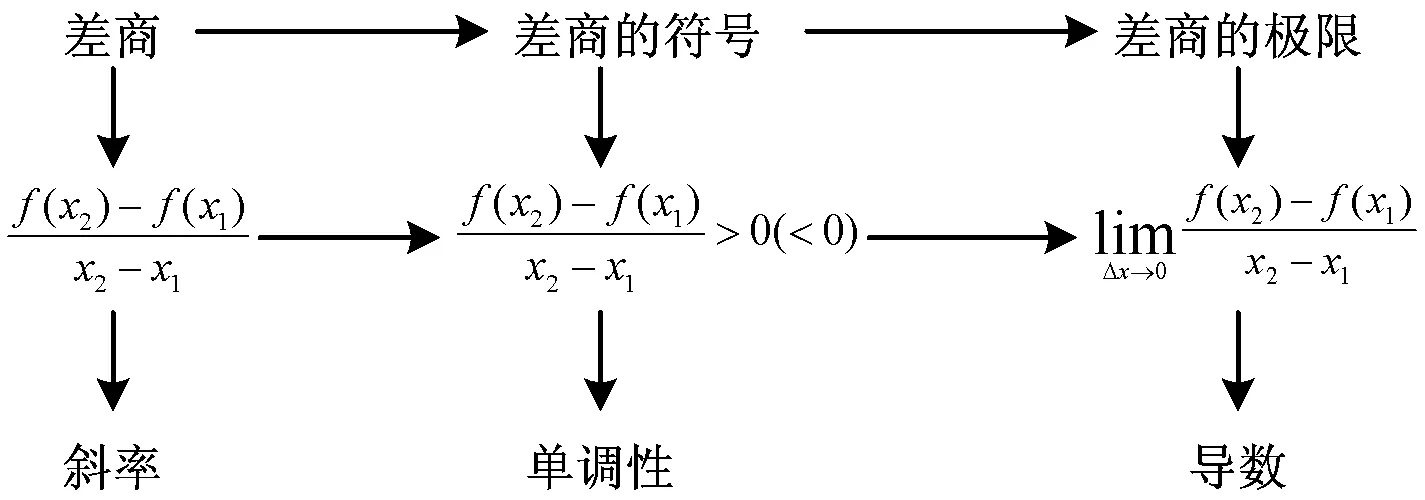
2 忘“形”得“一”,掌握一類(lèi)問(wèn)題的普適性解法
2.1 展“形”——表征圖形中元素位置形態(tài)

2.2 變“形”——變換圖形中元素及位置關(guān)系

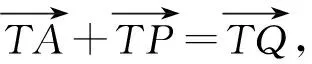
2.3 析“形”——整合相關(guān)圖形




2.4 得“一”——對(duì)模型本質(zhì)的概括與普適性解法的提煉



3 忘“形”得“一”,促進(jìn)對(duì)問(wèn)題的深刻性理解
3.1 展“形”——了解運(yùn)用的寬度

3.2 變“形”——擴(kuò)寬運(yùn)用的深度






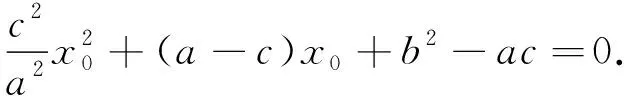





3.3 析“形”——建構(gòu)定理運(yùn)用的完備性認(rèn)識(shí)
3.4 得“一”——掌握定理運(yùn)用的本質(zhì)


4 結(jié)束語(yǔ)
