異構攜能通信網絡頑健資源分配算法

徐勇軍，胡圓，李國權，林金朝，陳前斌

（1. 重慶郵電大學通信與信息工程學院，重慶 400065；2. 重慶郵電大學生物醫學工程研究中心，重慶 400065）

1 引言

隨著通信終端業務呈現出多樣化、智能化和寬屏化的特點，移動設備的能量消耗變得尤為嚴重。然而能源日益枯竭的今天，尋找可再生能源成為社會發展的必然趨勢。為了降低二氧化碳排放并延長通信系統壽命，無線攜能通信（SWIPT, simultaneous wireless information and power transfer）技術應運而生[1]。SWIPT技術通過從周圍環境無線電信號中吸收電磁波能量，給設備進行充電從而延長設備壽命，提高通信系統的能量利用率。異構攜能通信網絡結合了 SWIPT技術和異構無線網絡的優勢，在提高網絡覆蓋范圍、減小通信盲區的同時，延長網絡運行壽命、實現綠色通信，因此成為當前5G通信技術的研究熱點[2]。

在異構攜能通信網絡中，如何有效地干擾管理、提升服務質量是實現多網共存的關鍵，因此資源分配技術被學術界廣泛研究[3]。文獻[4]針對由一個宏小區網絡和多個微小區組成的下行異構網絡，考慮跨層干擾約束、微小區基站的最大發射功率約束和區內干擾約束，提出了一種基于總速率最大化的資源分配算法。文獻[5]研究了基于正交頻分多址的異構網絡聯合功率控制和接入控制的資源分配算法，同時考慮對宏蜂窩用戶的干擾控制和次用戶設備的最小速率約束，旨在最大化網絡的頻譜效率和網絡能量效率。文獻[6]研究了下行異構無線網絡的鏈路傳輸問題，為了減小區間干擾和區內干擾，采用部分頻率復用（FFR, fractional frequency reuse）方式，提出了一種基于能量效率的節能資源分配算法。然而上述研究都是假設在完美信道狀態信息下實現異構無線網絡資源分配。在實際物理通信場景中，環境干擾、信道時延、估計誤差都會導致完美的信道狀態信息很難獲得。

針對上述問題，有很多學者開始研究異構無線網絡頑健資源分配問題。文獻[7]針對正交頻分復用的雙層異構網絡頑健功率控制問題，考慮每個飛蜂窩用戶鏈路上的不確定性，同時避免對宏蜂窩用戶帶來嚴重的跨層干擾約束，提出了用戶速率最大化的頑健功率控制算法。文獻[8]針對認知異構無線網絡中的能量消耗問題，考慮主用戶干擾控制和次用戶速率要求及用戶公平性約束，提出了一種基于啟發式算法的頑健資源分配算法。文獻[9]研究異構無線網絡下的多目標優化問題，考慮干擾信道不確定性的情況，尋找系統頻譜分配和功率分配的最優解，實現蜂窩用戶的能量效率/頻譜效率最大化。

隨著密集小區布局的深入，更多的飛蜂窩用戶接入宏蜂窩網絡頻譜資源，然而由于電池容量的有低蜂窩用戶，飛蜂窩用戶無法進一步提升自己的性能。因此，部分學者開始針對異構攜能通信網絡資源分配問題展開相關研究。文獻[10]研究了雙層異構攜能通信網絡的下行鏈路資源分配問題，采用時間切換和功率切換方法，在保障宏蜂窩小區用戶最小吞吐量的需求下，設定可變的干擾閾值來控制飛蜂窩網絡對宏蜂窩用戶造成的干擾，聯合優化能量收集速率與飛蜂窩網絡吞吐量。文獻[11]針對異構攜能網絡上行傳輸資源分配模型，考慮用戶最小速率需求約束和最大傳輸功率約束，在優化網絡資源（用戶數據速率）的同時最大化小蜂窩網絡的能量利用率，提出了基于雙層博弈理論的資源分配算法。然而上述工作并沒有考慮信道不確定性所帶來的影響，因此，研究異構攜能通信網絡聯合頑健功率控制和功率分流具有十分重要的理論意義。

本文考慮不完美信道狀態信息與非線性能量收集模型，研究雙層異構攜能通信網絡下行傳輸頑健資源分配問題。首先，考慮飛蜂窩基站最大發射功率約束、宏蜂窩用戶中斷概率約束和飛蜂窩用戶最小傳輸速率約束，建立飛蜂窩網絡能量利用率最大化的頑健資源分配模型。其次，針對含概率約束的非凸優化問題，采用最小最大概率機方法將中斷概率約束轉換為凸約束條件，并利用Dinkelbach原理將分式目標函數下的資源優化問題轉換為一個凸優化問題。再次，利用拉格朗日對偶原理獲得解析解，并進行頑健性能分析。最后，通過與傳統資源分配算法對比，仿真分析驗證了本文所提算法的有效性。本文主要貢獻如下。

1) 建立了基于能量收集的多用戶宏蜂窩-飛蜂窩異構攜能通信網絡模型。考慮飛蜂窩用戶最小速率約束、保護宏蜂窩用戶QoS的跨層干擾約束和最大發射功率約束，給出了用戶能量效率最大的資源優化問題。

2) 為了有效地保護宏蜂窩用戶性能，建立了頑健資源優化模型。與傳統假設已知不確定性參數統計模型不同，本文在假設未知不確定性參數模型條件下，已知參數估計誤差和方差，基于最小最大概率機方法，將傳統不易求解的非線性不確定性優化問題轉換為確定性的凸優化問題。

3) 將多變量優化問題分解為功率分配子問題和功率分流子問題，利用Dinkelbach方法將分式目標函數轉換為非分式形式，并利用拉格朗日對偶分解方法及次梯度更新算法來獲得解析解。

4) 仿真結果通過算法收斂性、能量效率和對比不同算法的頑健性來驗證本文所提算法的有效性。

2 系統模型

本文考慮由宏蜂窩和飛蜂窩組成的兩層異構無線網絡下行傳輸場景。系統中有一個宏蜂窩基站服務M個宏蜂窩用戶和一個飛蜂窩基站服務N個飛蜂窩用戶，如圖1所示。

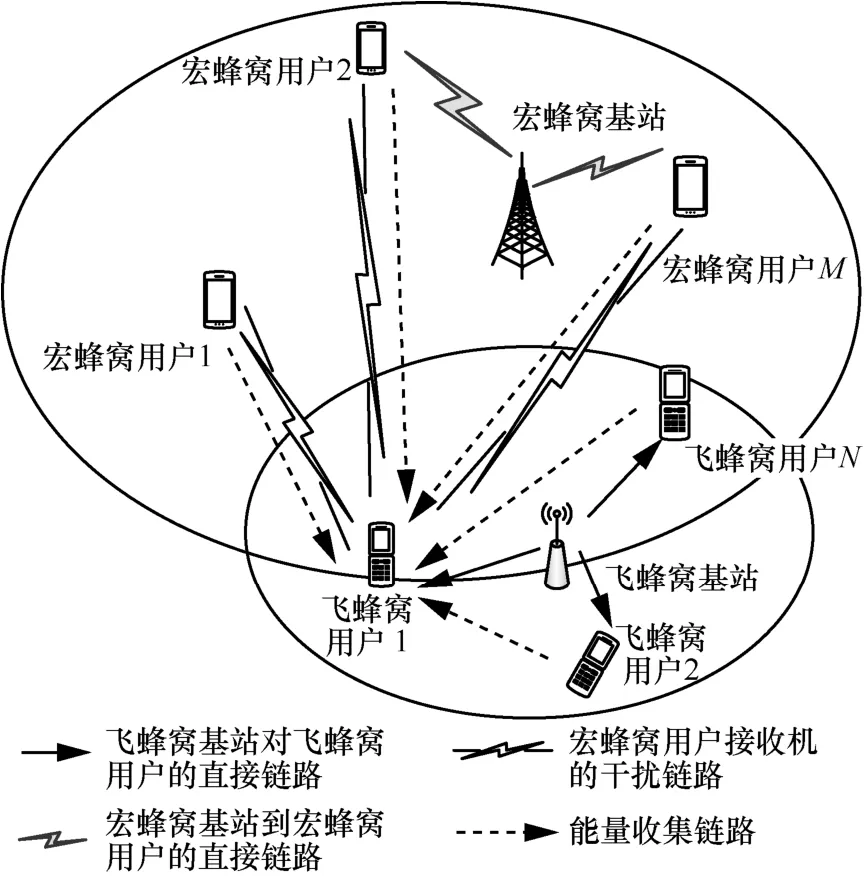
圖1 異構無線攜能通信網絡系統模型

宏蜂窩網絡是具有大覆蓋范圍、高功率的主網絡，是頻譜資源的擁有者，具有較高的頻譜資源利用優先級，因此任何其他網絡共存或用戶接入不應該對當前宏蜂窩網絡用戶的性能造成無法容忍的影響。飛蜂窩網絡是部署在宏蜂窩網絡覆蓋范圍內來解決密集節點傳輸與室內覆蓋盲區或通信質量差等問題的網絡，通常具有較低的頻譜利用權限。當飛蜂窩與宏蜂窩網絡共存時，彼此之間會出現跨層干擾（即非同層干擾）。因此，在功率分配或功率調節時，飛蜂窩用戶需要有效控制其傳輸功率的大小來避免對已經存在相同頻譜資源的宏蜂窩用戶帶來有害干擾。網絡共存的核心是既需要提高當前網絡性能，減小遮蔽效應帶來的影響，同時還需要保證當前網絡用戶能夠正常通信，減小中斷。假設飛蜂窩用戶設備具有SWIPT技術，通過提取接收信號的能量有效地向各種終端設備饋電，解決傳統有線供電或電池供電能量受限的不足。本文采用功率分流方案，在飛蜂窩用戶接收機端將接收到的信號分成兩部分：信息解碼信號和能量收集信號，并在信息解碼器和能量收集器中共享。定義宏蜂窩用戶集合 ?i∈ M ? { 1,2,…,M}和飛蜂窩用戶集合 ?j∈ N ? { 1,2,… ,N}。本文物理參數描述如表1所示。

在上述異構攜能網絡頻譜共享模式下，當宏蜂窩用戶是授權用戶時具有高的頻譜使用優先級，因此飛蜂窩在共享頻譜時，不能影響宏蜂窩用戶正常的通信質量。為了保護每個宏蜂窩用戶接收機的基本通信質量（即最小速率需求或最小信干噪比（SINR, signal to interference plus noise ratio）需求），網絡中所有飛蜂窩用戶對任意宏蜂窩用戶的干擾功率應該滿足

與此同時，由于飛蜂窩基站發射功率受到物理電路的條件限制，不可能提供無限大的能量，因此飛蜂窩基站傳輸功率同時應滿足

考慮宏蜂窩網絡與飛蜂窩網絡間的跨層干擾和飛蜂窩內部之間的多址干擾，每個飛蜂窩用戶接收機端實際接收到的信干噪比可以描述為

表1 本文物理參數描述

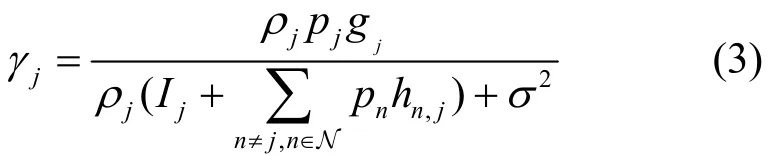
其中，ρj∈[0,1]為信號功率中信息信號的比例系數。

基于香農定理[12]，飛蜂窩用戶j的傳輸速率可以表示為

同時，為了保證每個飛蜂窩用戶的基本服務質量，假設每個飛蜂窩用戶滿足某一最小傳輸速率約束要求，即

隨著 SWIPT技術的引入，在功率消耗部分可以通過收集到的能量進行功率補償，因此，基站處總功率消耗可以描述為

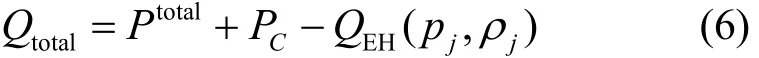
其中，0＜θ＜1為能量收集效率，Aj=Ij+

基于上述分析，假設系統參數能夠精確得到，可以得到異構攜能通信網絡能量效率最大化的資源分配問題為

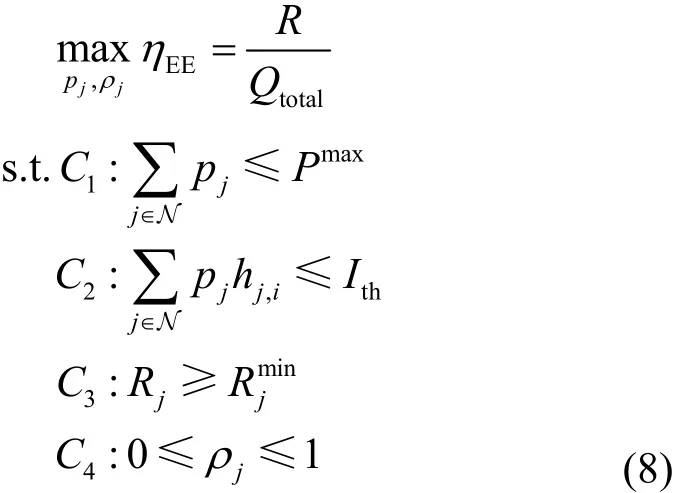
3 頑健資源分配

為了最大限度地保護宏蜂窩用戶的通信質量，本文考慮飛蜂窩基站發射機到宏蜂窩用戶接收機鏈路上的信道不確定性，因為該不確定性可能對宏蜂窩用戶造成無法容忍的干擾。因此，為了提高系統的頑健性，需要將系統的冗余性提前考慮到資源分配算法設計中，本文假設在信道不確定性的條件下，宏蜂窩用戶能夠容忍一定的中斷概率。因此基于干擾中斷概率約束的頑健資源分配問題描述為

其中，εi∈[0,1]為宏蜂窩用戶i的中斷概率閾值。由于C2概率約束的引入，式(9)是一個難以求解的NP-hard問題。

3.1 隨機優化問題

針對概率約束處理方式，已經有很多文獻研究過松弛概率積分[14]和伯恩斯坦方法（Bernstein approximation method）[15]，然而上述2種方法都需要知道不確定參數的精確概率統計分布模型。在實際的異構無線網絡場景中，隨著用戶接入的動態變化和信道衰落的影響，得到這些不確定參數的準確統計模型往往難以實現，因此，需要引入最小最大概率機方法來求解隨機參數概率分布模型未知的不確定性概率約束轉化問題。考慮式(10)所示的概率約束問題

其中，inf表示下確界；y表示不確定性變量；ε∈ [ 0,1]表示中斷概率，即在參數y存在不確定性的條件下，仍然使不等式保持成立的最大概率閾值。假設隨機變量y的均值和方差分別用y和E表

示，可以得到

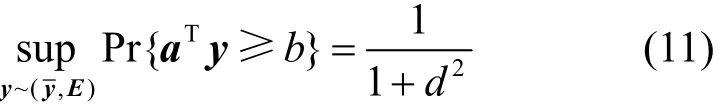
其中，有

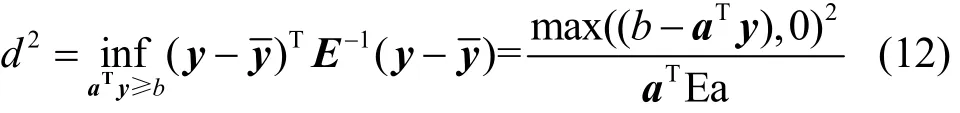
根據上述分析，可以得到

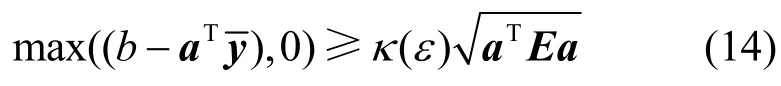
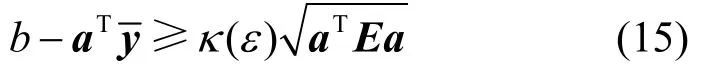
由于本文考慮飛蜂窩基站發射機到宏蜂窩用戶接收機鏈路上的信道不確定性，即干擾信道增益存在擾動的情況下，hj,i可以當作一個隨機變量。定義hj,i的均值和方差分別為和Ej,i，通過上述分析，可以將不確定性約束條件C2轉換為

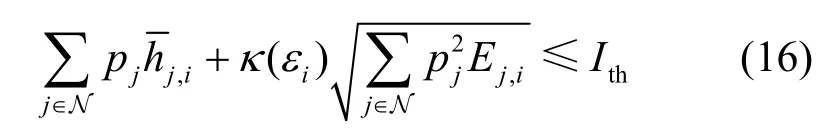
利用柯西不等式[16]對進行放縮處理，有

則式(16)可轉換為

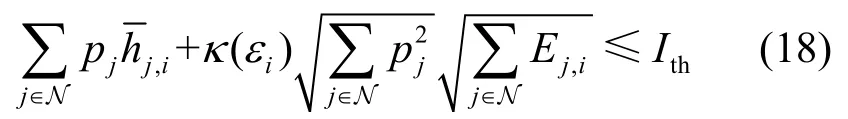
令考慮最壞情況（worst-case）準則，則式(18)的等價形式為

利用不等式縮放性質

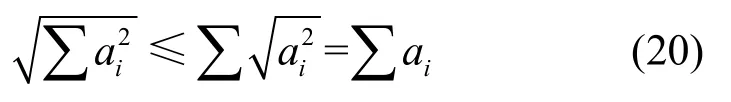
可以得到

則優化問題式(9)可變為

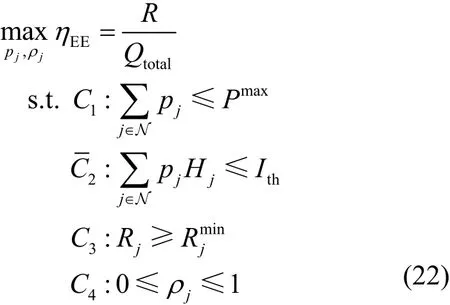
3.2 頑健資源分配問題

根據能量效率的定義可知，目標函數是一個分式規劃問題，因此，式(22)是一個非線性規劃問題，根據Dinkelbach方法[17]，將目標函數轉換成參數相減的形式，即

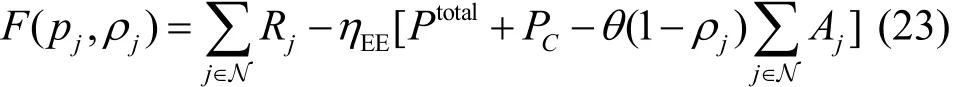
為了獲得式(22)的解析解，需要將其轉換成凸優化的形式，得到如下資源分配問題。

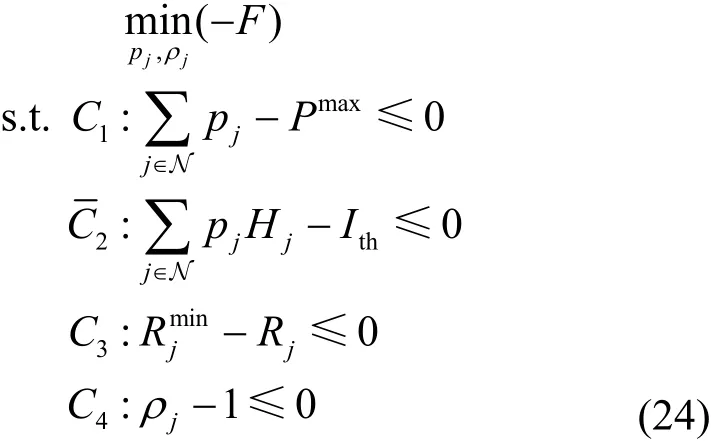
由于約束條件C1、C2和C4為線性約束條件，根據凸優化函數和凸條件定義[18]，該約束為凸約束。由于飛蜂窩通常情況下采用低功率節點傳輸，因此約束條件C3和目標函數的凸性可以通過優化變量的海森矩陣正定性證明得到[19-21]。另外，函數Rj是關于優化變量ρj的單調遞增函數，是一個凸優化問題。綜上所述，優化問題式(24)變成了可求解的凸優化形式。本文聯合優化發射功率pj與信息信號系數ρj，采用雙循環變量法，將原優化問題分解成2個等價的子問題進行求解。

4 頑健資源分配算法求解

4.1 功率分配求解

針對式(24)的凸優化問題，利用拉格朗日對偶原理[22]，可以求解該問題。構建關于功率分配因子pj的拉格朗日函數，如式(25)所示。

其中，λ、?和νj分別是約束條件和C3所對應的非負拉格朗日乘子。式(25)的對偶函數可以寫為

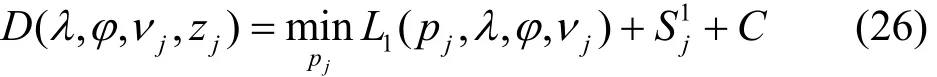
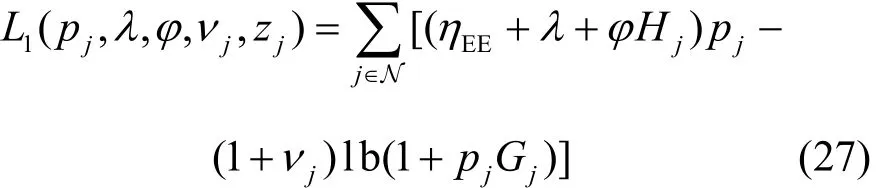
4.2 信息系數求解

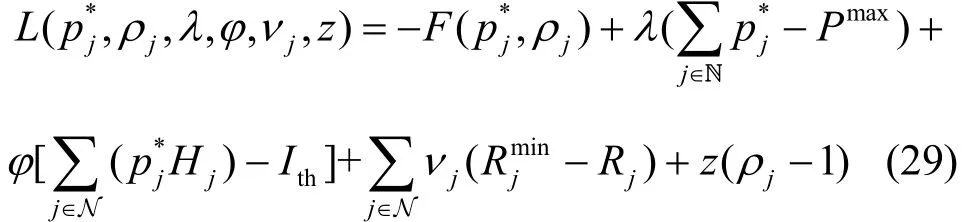
其中，z是約束條件C4對應的拉格朗日乘子。根據拉格朗日對偶原理，得出對偶函數為

式(29)中以拉格朗日乘子為優化變量的對偶優化問題計算式為

根據次梯度更新算法，得到拉格朗日因子的更新式為

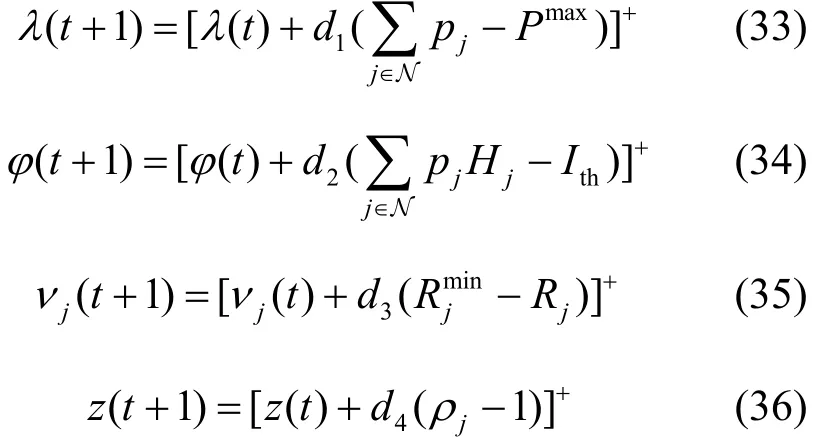
其中，t表示迭代次數，d1≥0，d2≥0，d3≥0和d4≥ 0 為步長，通過選擇合適的步長，可以保證次梯度更新算法的收斂性[23]。

綜上所述，本文提出的基于能量效率的頑健資源分配算法步驟如算法1所示。

算法1 頑健資源分配算法

1) 初始化系統參數d1≥0，d2≥0，d3≥0，d≥ 0 ，I＞0，Pmax＞0，Rmin＞0，p＞ 0 ，設

4thjj定網絡用戶數和最大迭代次數為T，算法收斂精度為ξ。初始化功率分流系數ρj＞0，初始化能量效率ηEE，初始化迭代次數t=0。

4) 判斷飛蜂窩基站發射功率總和、宏蜂窩用戶接收機收到的干擾、飛蜂窩用戶傳輸速率等是否滿足設定閾值值，若都滿足，則繼續；否則，返回步驟2)。

5) 根據式(32)得到次優功率分流比系數*

jρ。

6) 更新迭代次數t=t+1。

7) 若t≥T，則終止；否則，計算能量效率ηEE(t+ 1 )，返回步驟3)。

4.3 復雜度和靈敏度分析

本節考慮由飛蜂窩網絡和宏蜂窩網絡構成的異構無線網絡，提出了聯合發射功率和信息系數的飛蜂窩網絡能量利用率最大化的頑健資源分配算法。假設算法收斂最大迭代次數為T，飛蜂窩用戶個數為N。根據式(28)、式(32)～式(36)可知，在同層循環內，主變量pj、jρ和jν需要的計算復雜度為O(N)，而其他拉格朗日乘子需要的計算復雜度為O(1)。又因為Dinkelbach外循環求解的最大計算復雜度是一個超線性時間復雜度形式O(T)[24]，因此本文算法的多項式時間復雜度為O(NT)。

由于本文考慮鏈路j上飛蜂窩用戶到鏈路i上宏蜂窩用戶的干擾信道增益不確定性，實際的干擾信道增益定義為其中，表示干擾信道增益估計值，Δhj,i表示干擾信道增益的攝動值。由于本文提前將參數不確定性考慮進來，則會犧牲一定的能量效率性能來保障系統的頑健性。分別表示名義優化模型和頑健資源分配模型下的能量效率值，因此，能量效率犧牲的代價可以用來衡量。

其中，有

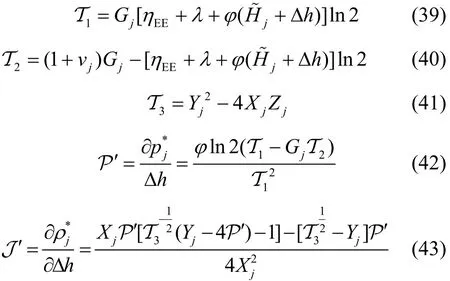
綜上，結合式(37)與式(38)可以得到

5 仿真結果與分析

本節為了驗證所提算法的有效性，在相同仿真環境下，從不同角度對比分析基站發射功率閾值、干擾功率閾值參數對系統能量效率和中斷概率的影響。中斷概率的定義式為

假設用戶均隨機分布在基站的周圍，為了驗證本文算法的快速收斂性，假設飛蜂窩網絡中存在2個飛蜂窩用戶，即N=2。從圖2(a)中可以看出，本文所提算法具有很好的收斂性，飛蜂窩基站通過不斷調整對飛蜂窩用戶的發射功率，來保障飛蜂窩用戶的通信質量，同時總發射功率并沒有超過最大發射功率閾值。同時，從圖 2(b)中可以看出，飛蜂窩用戶對宏蜂窩用戶產生的干擾并沒有超過干擾功率閾值，從而也可以保證宏蜂窩用戶的通信質量。

表2 仿真參數

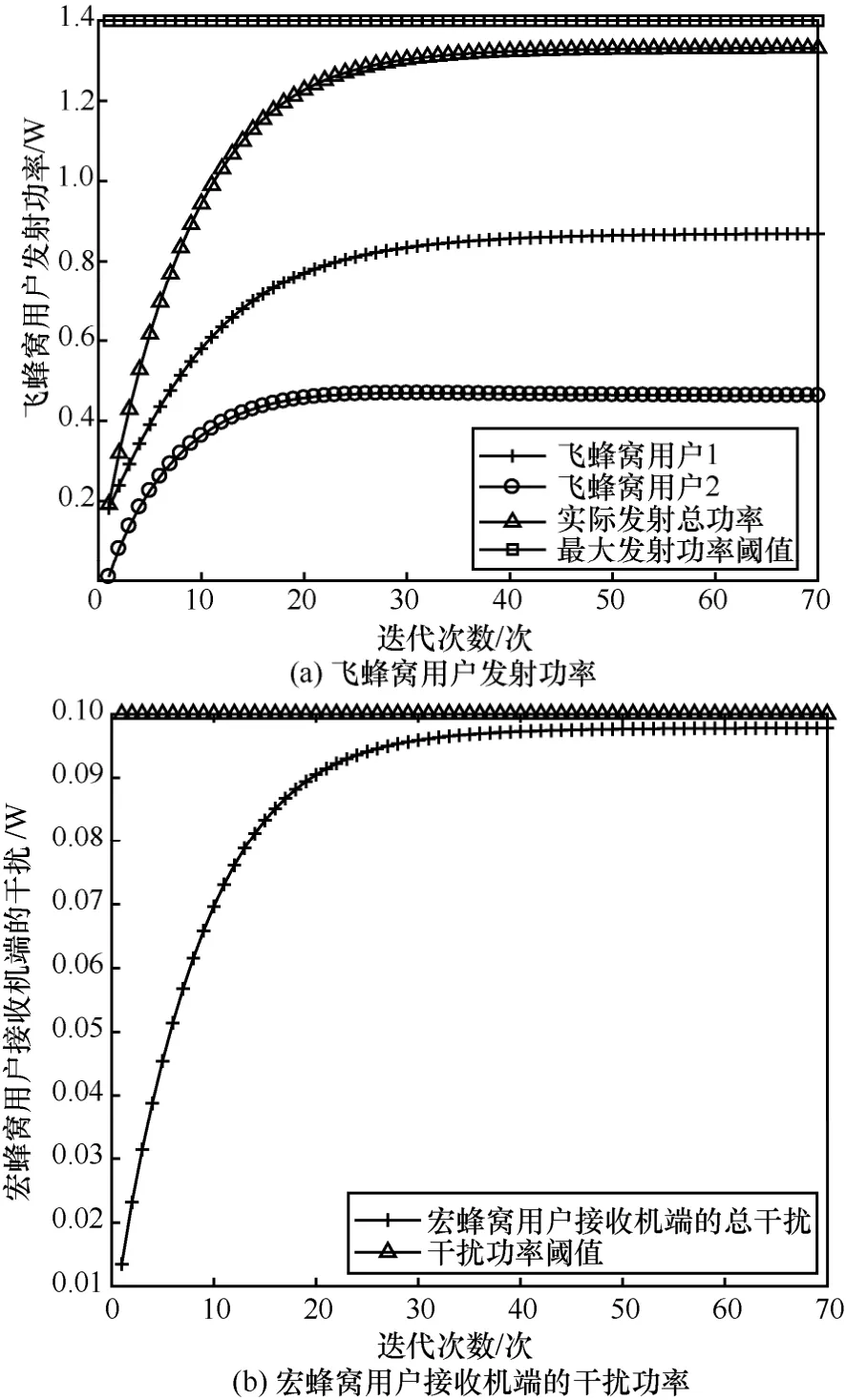
圖2 飛蜂窩用戶發射功率收斂性和宏蜂窩用戶接收機端干擾功率控制

為了研究飛蜂窩基站最大發射功率和系統電路損耗功率對能量效率的影響，假設其他系統參數相同。從圖3中可以看出，當電路損耗功率值不變時，飛蜂窩網絡的能量效率隨著最大發射功率閾值的增加而增加。因為發射功率閾值越大，允許飛蜂窩基站對用戶的發射功率越大，傳輸速率越快，從而系統容量隨之增加，飛蜂窩網絡能量效率增加。當系統最大發射功率值一定時，隨著電路損耗功率的增加，能量效率顯然會隨之減小，電路損耗功率越大，整個系統消耗的功率越多。

圖3 電路損耗功率和最大發射功率閾值對能量效率的影響

為了驗證信道參數對能量效率的影響，假設其他系統參數不變，圖4說明了干擾信道增益參數（方差、均值）對能量效率的影響。從圖4中可以看出，當均值一定時，方差Ej,i越大，能量效率越小。因為方差值越大說明這組信道參數偏離均值的程度越大，信道環境越差，從而導致系統能量效率降低。同時，當方差值一定時，能量效率隨著均值的增加而減小，均值越大，說明干擾信道增益越大，對宏蜂窩用戶接收機產生的干擾越大，因此，系統能量效率降低。

圖4 信道參數方差和均值對能量效率的影響

為了進一步驗證本文所提算法的有效性，從系統性能和收斂性兩方面，將本文所提算法與不同算法進行對比分析。從圖5(a)中可以看出，隨著迭代次數的增加，4種算法都逐漸趨于收斂值，但是本文所提算法趨于收斂值時的迭代次數最低，即收斂性最好。因為采用伯恩斯坦近似法會設定大量參數，從而提高了算法的復雜度，所以收斂性較差。同時從圖5(b)中可以看出，隨著信息系數的增加，4種算法下的能量效率都隨之降低。因為信息系數越大，從干擾信號中收集的能量越多，導致飛蜂窩用戶的信干噪比降低，從而影響飛蜂窩用戶的通信質量。結合圖 5(a)和圖5(b)可以看出，本文所提算法 MREA的能量效率是最高的，因為WREA是考慮最壞情況下的資源分配，雖然避免了用戶發射中斷的情況，但是卻犧牲了能量效率，同時MRRA由于考慮速率最優，卻忽略了最小化功率損耗部分。

圖5 不同算法下的能量效率對比

圖6描述了在干擾功率和信道參數影響下，不同算法下的中斷概率對比值。圖6(a)中對比的3種算法都是頑健資源分配算法，可以看出，在干擾功率閾值一定的情況下，本文所提算法的中斷概率是最低的，并且中斷概率隨著干擾功率閾值的增加而減小。因為干擾功率閾值越大，宏蜂窩用戶接收機端可以容忍的干擾越大，因此，宏蜂窩用戶發生的中斷概率降低。

另外，為了驗證本文所提算法的頑健性，考慮信道擾動參數對中斷概率的影響，實際干擾信道增益為其中為信道估計值，Δhj,i為擾動參數。從圖6(b)中可以觀察到，隨著擾動參數的增加，中斷概率隨之增加。因為擾動參數越大，信道增益波動越大，則宏蜂窩用戶發生中斷的概率變大。同時，可以看出，本文所提的頑健能量效率優化算法的中斷概率最低，非頑健算法中斷概率最高。因為頑健算法提前將參數不確定性考慮進去，可以減小用戶發生中斷的概率，保障了系統的頑健性。

圖6 不同算法下干擾功率和信道參數對中斷概率的影響

為了進一步驗證算法的有效性，圖7給出了已知統計模型處理方法與本文在不同估計誤差和中斷概率方面的能量效率對比。定義情況1為基于高斯隨機變量的頑健算法，情況2為基于均勻分布的頑健算法。圖7表明，在固定中斷概率閾值要求下，隨著估計誤差方差的增大，3種算法的能量效率都增加。本文所提的MREA明顯好于另外2種已知概率分布下的頑健算法。因為無線信道的隨機性和量化誤差影響，并不能保證估計誤差時刻滿足高斯分布或均勻分布特性，因此本文算法更具有一般性。圖8表明，隨著中斷概率閾值要求增加，3種算法的能量效率都減小，并且本文所提的MREA好于另外2種算法。由于實際系統模型失配（即算法假設模型與實際系統模型不符），會使已知模型算法性能降低。

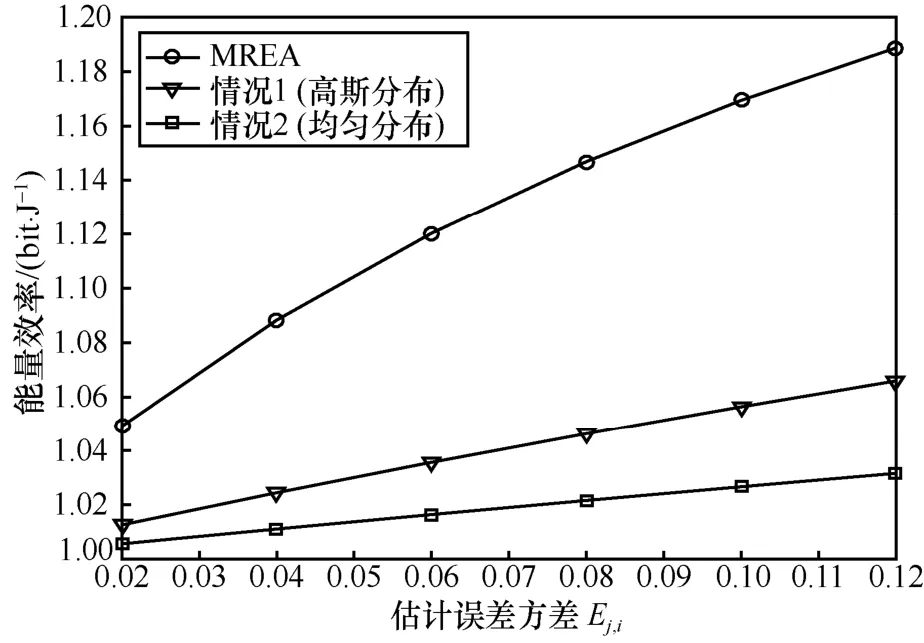
圖7 估計誤差對能量效率的影響

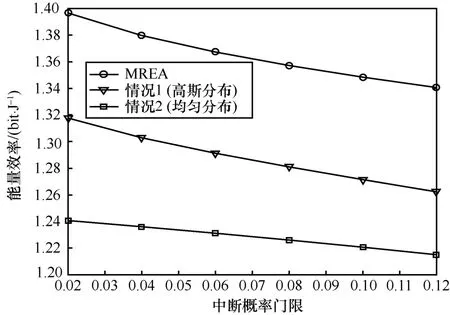
圖8 中斷概率閾值對能量效率的影響

6 結束語

本文以提高飛蜂窩網絡系統能量利用率為目標，研究了信道不確定性下的異構攜能網絡頑健資源分配問題，考慮飛蜂窩基站最大發射功率約束及用戶最小速率約束、宏蜂窩用戶接收機干擾約束，提出了一種聯合功率和信息系數分配的頑健資源分配算法。由于求解最大化能量利用率的效用函數屬于非線性規劃問題，本文利用Dinkelbach方法，將原分式規劃問題轉換成線性規劃形式，并基于最小最大概率機方法，將原機會式約束條件轉換成凸優化形式。最后將發射功率和信息系數的聯合優化過程分解成2個等價的迭代子問題進行求解。仿真結果表明，本文所提的頑健資源分配算法在保障飛蜂窩用戶和宏蜂窩用戶的通信質量前提下，能夠有效地提升飛蜂窩網絡的能量利用率，并且能較好地保障系統的頑健性。