離散Fréchet 距離在強震臺站場地 分類中的應用1

梁基冠 程 印 趙 岑

（西南交通大學，土木工程學院，成都 610031）

引言

在地震工程中，強震臺站的場地分類具有重要意義，合理地劃分強震臺站的場地類別為進一步應用強震數據奠定基礎（王珊等，2014）。采用合適的指標和適當的方法劃定強震臺站場地類別是地震工程中的一項重要課題。獲取臺站鉆孔資料時，利用鉆孔資料計算相應參數，并將這些參數與各類指標進行比對便可劃分場地類別（中華人民共和國住房和城鄉建設部等，2010；Building Seismic Safety Council，2003；Ministry of Land，Infrastructure，Transport and Tourism，2007；蔣其峰等，2017）。

無法獲取場地鉆孔資料時，可用譜比法等經驗方法對場地進行大致分類（Borcherdt，1970；Zhao 等，2006；Wen 等，2011；溫瑞智等，2015）。經典譜比法需參考場地（Borcherdt，1970），由于參考場地選取不便，有研究者提出無需參考場地的方法，如Nakamura（1989）將橫豎向地脈動的傅里葉譜相比以識別場地特性；Lermo 等（1993）、Yamazaki 等（1997）將該方法運用到強震臺站場地分類中；Zhao 等（2006）使用5%阻尼比下的橫豎向加速度反應譜比進行場地分類，利用阻尼比產生的“一致”平滑效果，避免傅里葉譜平滑操作帶來的影響；Fukushima 等（2007）將Zhao 等（2006）的方法應用于建立地震動衰減關系，認為用該方法劃分場地類別可降低衰減關系的標準差，表明使用譜比法劃分場地類別具有獨特的合理性和適用性。利用橫豎向反應譜比法對場地進行分類，關鍵在于將待分類場地的平均反應譜比曲線與各類場地的標準反應譜比曲線相匹配，不同的匹配方法對最終分類結果有很大影響（Zhao 等，2006；Ghasemi 等，2009；Wen 等，2011；溫瑞智等，2015；趙萬松，2017）。因此，對現有匹配方法進行改進，以期達到更好的分類效果是當前使用譜比法進行場地分類研究的熱點問題。利用待分類場地譜比曲線與標準譜比曲線之間的相似性可對場地進行分類。Fréchet 距離是一種判別2 條曲線相似性的工具（Alt 等，1995），兩曲線間的Fréchet 距離越小則越相似。Alt 等（1995）提出計算兩多邊形鏈的連續Fréchet 距離算法；Eiter 等（1994）提出兩多邊形鏈的離散Fréchet 距離算法，并認為離散Fréchet 距離可作為連續Fréchet 距離的近似；Eiter 等（1994）提出的“耦聯法”具有概念明確、計算效率高等特點，因而本文采用該方法計算離散Fréchet 距離，并以此為基礎進行場地分類。

首先基于《建筑抗震設計規范（GB 50011—2010）》對從日本KiK-net 強震臺網獲取的664 個具有鉆孔資料的強震臺站進行場地分類，構建2 個數據集，并求得數據集中各條記錄的橫豎向反應譜比。在此基礎上，計算數據集1 中各類場地的標準譜比曲線和數據集2 中的各臺站平均譜比曲線。最后，基于離散Fréchet 距離重新劃分數據集2 中各臺站的場地類別，并統計此方法分類結果，通過與斯皮爾曼秩相關系數法進行對比，并將應用本文方法分類得到的平均譜比曲線與標準譜比曲線進行對比，以校驗本文分類方法的合理性。

1 離散Fréchet 距離

離散Fréchet 距離是連續Fréchet 距離的一種近似，用多邊形鏈近似代替曲線，通過計算兩多邊形鏈間的Fréchet 距離，并以此作為兩曲線間Fréchet 距離的近似。根據Eiter 等（1994）提出的“耦聯法”，在某種情況下將兩多邊形鏈P、Q的節點連接起來（即速度組合）：

2 KiK-net 臺站標準譜比曲線

2.1 Kik-net 臺站場地分類

《建筑抗震設計規范（GB 50011—2010）》使用“雙指標”劃分場地類別，即由場地覆蓋層厚度和等效剪切波速共同決定場地類別。《建筑抗震設計規范（GB 50011—2010）》中，I類場地被劃分為I0和I1兩個亞類，為保證數據量足夠多，本文將二者合為I 類。

日本KiK-net 強震臺網由692 個臺站組成，分布在日本各地，各臺站均有深達基巖的鉆孔數據（鉆孔深100m 左右）。各臺站均由2 組三分量加速度計組成，分布于地表及孔底（Okada等，2004）。自臺網運行以來，收集到大量地震動數據，對研究場地效應、地震動衰減模型等具有重要意義。按照《建筑抗震設計規范（GB 50011—2010）》中場地分類方法，對664 個KiK-net 臺站進行場地劃分，分類結果如表1 所示，臺站分布如圖2 所示。由于IV 類場地數量較少且《建筑抗震設計規范（GB 50011—2010）》中IV 類場地基本為深軟場地，我國強震臺站處于該類場地的可能性較小（溫瑞智等，2015），本文只制作I、II、III 類場地標準譜比曲線。

表1 KiK-net 臺站場地分類結果 Table1 Classification result of KiK-net stations

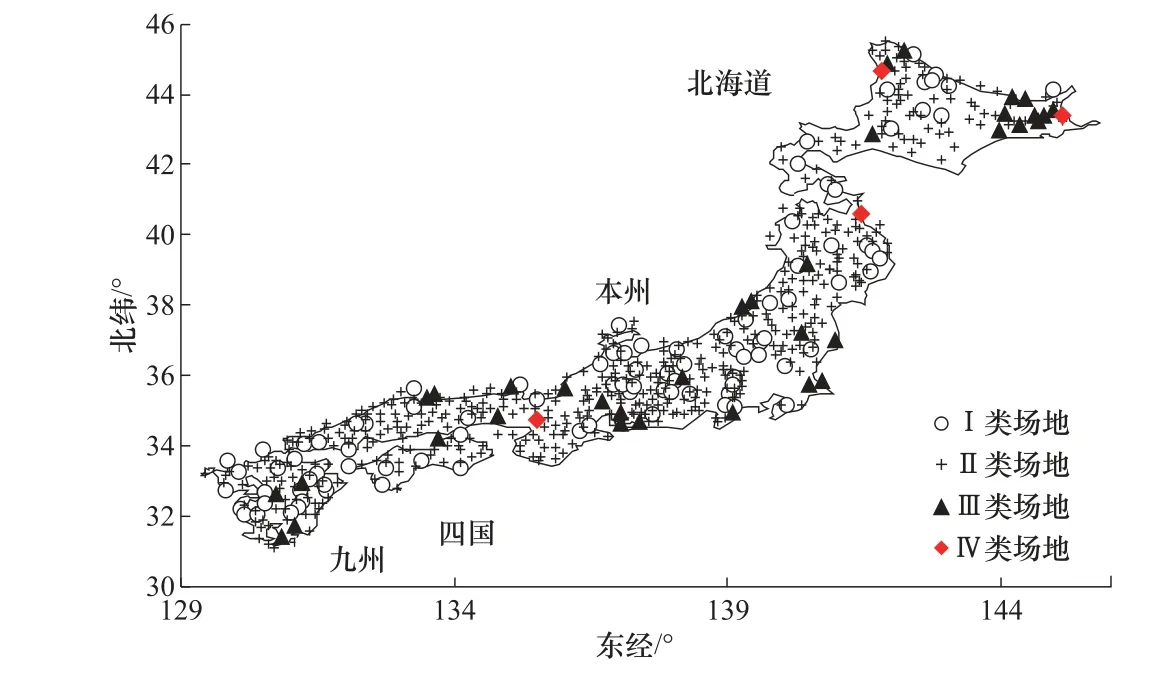
圖2 Kik-net 臺站場地類別及分布 Fig.2 Site class and distribution of Kik-net stations

在I、II、III 類場地臺站中隨機選定數據集1 的臺站，剩下的臺站歸入數據集2。數據集1 選取大部分臺站，用于獲取對應場地類別的標準橫豎向反應譜比曲線；數據集2 用于計算所選臺站的平均橫豎向反應譜比曲線，并利用本文分類方法重新劃分臺站場地類別，如表2所示。

表2 地震動記錄選取信息 Table2 Details on ground motion record selection

2.2 標準譜比曲線

分別計算數據集1 中每條地震動記錄3 個分量5%阻尼比下的加速度反應譜，對2 個水平分量的反應譜值進行幾何平均，再將幾何平均值與豎向反應譜值相比，即可獲得單條記錄的譜比曲線。對于某一類場地，將該類場地上所有的橫豎向反應譜比曲線求幾何平均，可得到該類場地標準譜比曲線。對數據集1 中的地震動記錄進行計算，得到I、II、III 類場地標準譜比曲線及自然對數標準差曲線，如圖3 所示。Zhao 等（2006）及其他研究者（Ghasemi 等，2009）的研究均表明，不同震級、距離下的譜比曲線區別不大，因此譜比曲線主要反映場地效應。由圖3（a）可知，I 類場地標準譜比曲線在反應譜周期為0.1 s 時達到最大值，最大值為2.4 左右，峰值區為0.07—0.12 s，整體趨勢為先升后降；II 類場地標準譜比曲線在反應譜周期為0.2s 時達到峰值，峰值為2.5 左右，峰值區為0.15—0.25s，整體趨勢也為先升后降；III 類場地標準譜比曲線有2 個峰值區，第1 個峰值區為反應譜周期0.12s 附近，第2 個峰值區為0.4—1.05s，峰值為2.8 左右，III 類場地峰值區范圍較I、II 類場地廣，III 類場地標準譜比曲線最大值出現在反應譜周期為0.5s 時。總體上，本文得到的3 條標準譜比曲線具有良好的區分度。由圖3（b）可知，本文得到的3 類場地標準譜比曲線自然對數標準差為0.36—0.60，且隨著周期的增加，各類場地自然對 數標準差逐漸穩定，其范圍與其他研究者的結果較為接近（Zhao 等，2006；Ghasemi 等，2009；溫瑞智等，2015）。因此，本文所得的標準譜比曲線及其自然對數標準差具有合理性。

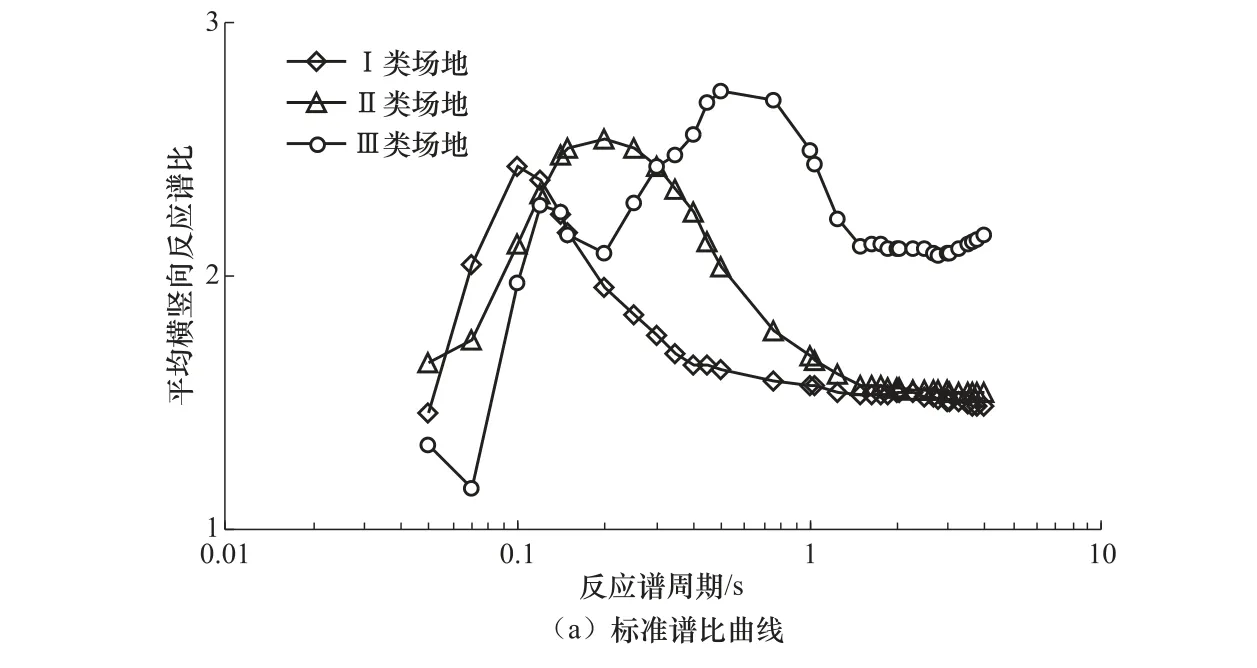
圖3 3 類場地標準譜比曲線及其自然對數標準差曲線 Fig.3 Standard spectra ratio curves and natural logarithmic standard deviation for three site classses

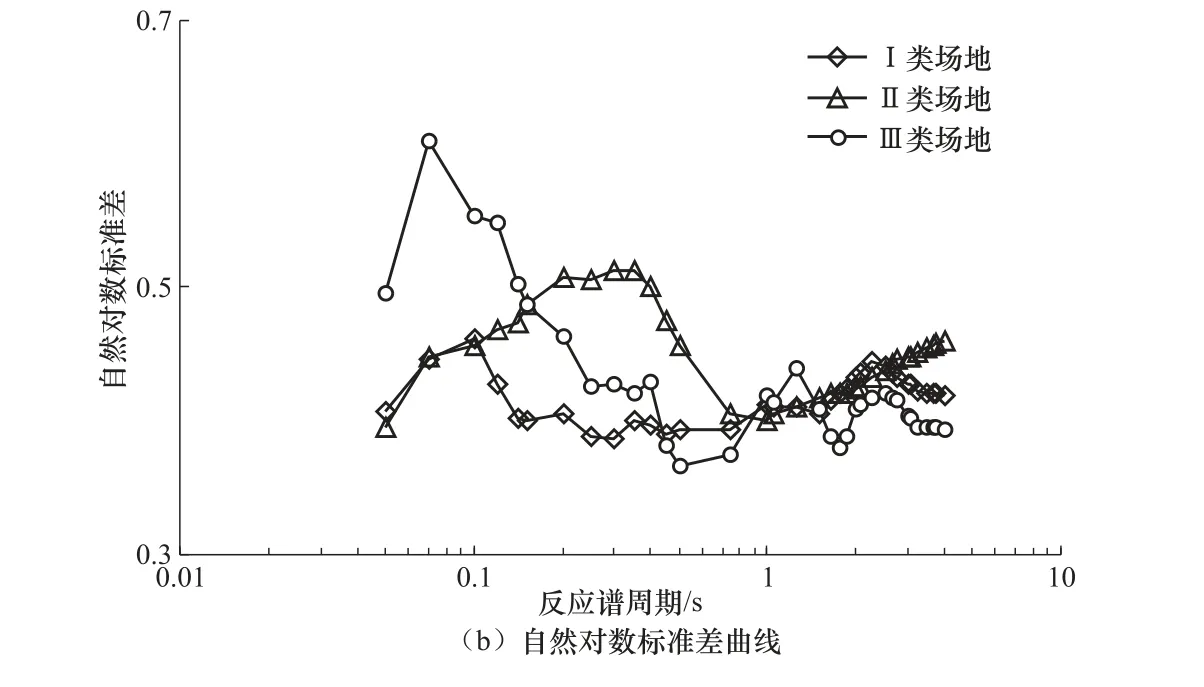
圖3 3 類場地標準譜比曲線及其自然對數標準差曲線 Fig.3 Standard spectra ratio curves and natural logarithmic standard deviation for three site classses

3 場地分類結果與校驗

3.1 場地劃分算例

根據離散Fréchet 距離概念及算法，結合本文得到的3 條標準譜比曲線劃分場地類別。本例選用KiK-net 臺站KGWH03 鉆孔信息，根據《建筑抗震設計規范（GB 50011—2010）》，由鉆孔信息劃分場地類別，結果如表3 所示。

表3 KGWH03 場地鉆孔及場地分類 Table3 Boring Information and Site Classification of KGWH03

使用本文方法對KGWH03 進行場地劃分，結果如圖4 所示。由圖4 可知，場地KGWH03平均橫豎向反應譜比曲線總體上較為平坦，在0.07s 附近達到峰值，然后逐漸下降，0.1s 后的下降趨勢基本與I 類場地平均譜比曲線一致。KGWH03 譜比曲線在0.1s 時出現凹陷，主要由該場地的數據分布造成。此外，單個場地與整類場地的數據量差異也是造成凹陷的原因之一。II 類場地標準譜比曲線峰值出現在0.2s，整個曲線的形狀與KGWH03 平均譜比曲線差異較大。而III 類場地標準譜比曲線具有2 個峰值，下降段斜率更大，與KGWH03 平均譜比曲線差異明顯。總的來說，KGWH03 平均譜比曲線與I 類場地標準譜比曲線最為相似。算得KGWH03 平均譜比曲線與I、II、III 類場地離散Fréchet 距離分別為0.777、0.923、1.321（見圖4），因此可將KGWH03 劃分為I 類場地。由本例可知，譜比曲線間的相似度越高，離散Fréchet 距離越小，利用Fréchet 距離可較合理地劃分場地類別。需注意的是，本例中KGWH03平均譜比曲線與3 條標準譜比曲線的離散Fréchet 距離恰好為標準譜比曲線峰值與對應周期上平均譜比曲線的差值，但對于其他臺站可能并非如此，須根據“耦聯法”計算結果具體分析。

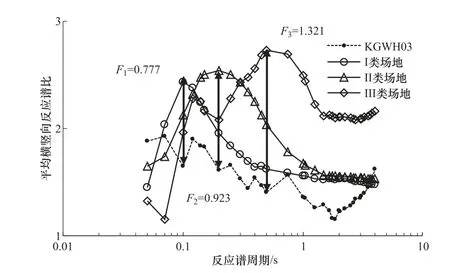
圖4 離散Fréchet 距離場地分類算例 Fig.4 Site classifications using discrete Fréchet distance

3.2 場地劃分結果對比

式中di為第i個反應譜周期處待分類場地平均譜比曲線與標準譜比曲線間的差；n為反應譜所用周期點數。ρ越接近1 表示兩曲線越相似。

使用本文基于離散Fréchet 距離的場地分類方法及斯皮爾曼秩相關系數法分別對數據集2 中的場地進行分類，統計分類成功率及誤判率，結果如圖5 所示。當本文方法將數據集2 中的I、II、III 類場地重新劃分為I、II、III 類時即為成功，否則為失敗。圖5 中，橫坐標“II 類場地”表示重新對數據集2 中的場地進行分類，最終結果顯示為II 類場地的部分。

由圖5 可知，使用本文方法時，I 類場地成功率為56.00%，低于斯皮爾曼秩相關系數法所得68.00%的成功率。本文方法P12=24.00%，P13=20.00%；而斯皮爾曼秩相關系數法P12=24.00%，P13=8.00%。可知本文方法將I 類場地誤判為II、III 類場地的概率接近，而斯皮爾曼秩相關系數法主要將I 類場地劃分為I、II 類場地。造成此種差異的原因為本文數據集中I 類場地平均譜比曲線受數據量不足的影響，其形狀與I 類場地標準譜比曲線差異較明顯，某些場地的平均譜比曲線可能凹凸較多，其與I 類場地標準譜比曲線的離散Fréchet 距離大于II、III 類場地，造成誤判。而斯皮爾曼秩相關系數法則是對2 條曲線間的差值求和，一般來說I類場地平均譜比曲線的值均小于I 類場地標準譜比曲線的值，而II、III 類場地標準譜比曲線的值則比I 類場地標準譜比曲線的值大，所以更易區分。對于II 類場地，斯皮爾曼秩相關系數法劃分成功率為39.39%，小于本文方法，且斯皮爾曼秩相關系數法P23=42.42%，即成功率與誤判率接近，說明斯皮爾曼秩相關系數法難以準確區分II、III 類場地；而本文方法則不然，不僅劃分成功率較高，且誤判率和成功率之間的差異也較大，即誤判風險較小。對于III類場地，本文方法劃分成功率為75.00%，大于斯皮爾曼秩相關系數法，說明本文方法在對III類場地的劃分上較優。因此，本文方法總體表現較好，具有一定合理性。

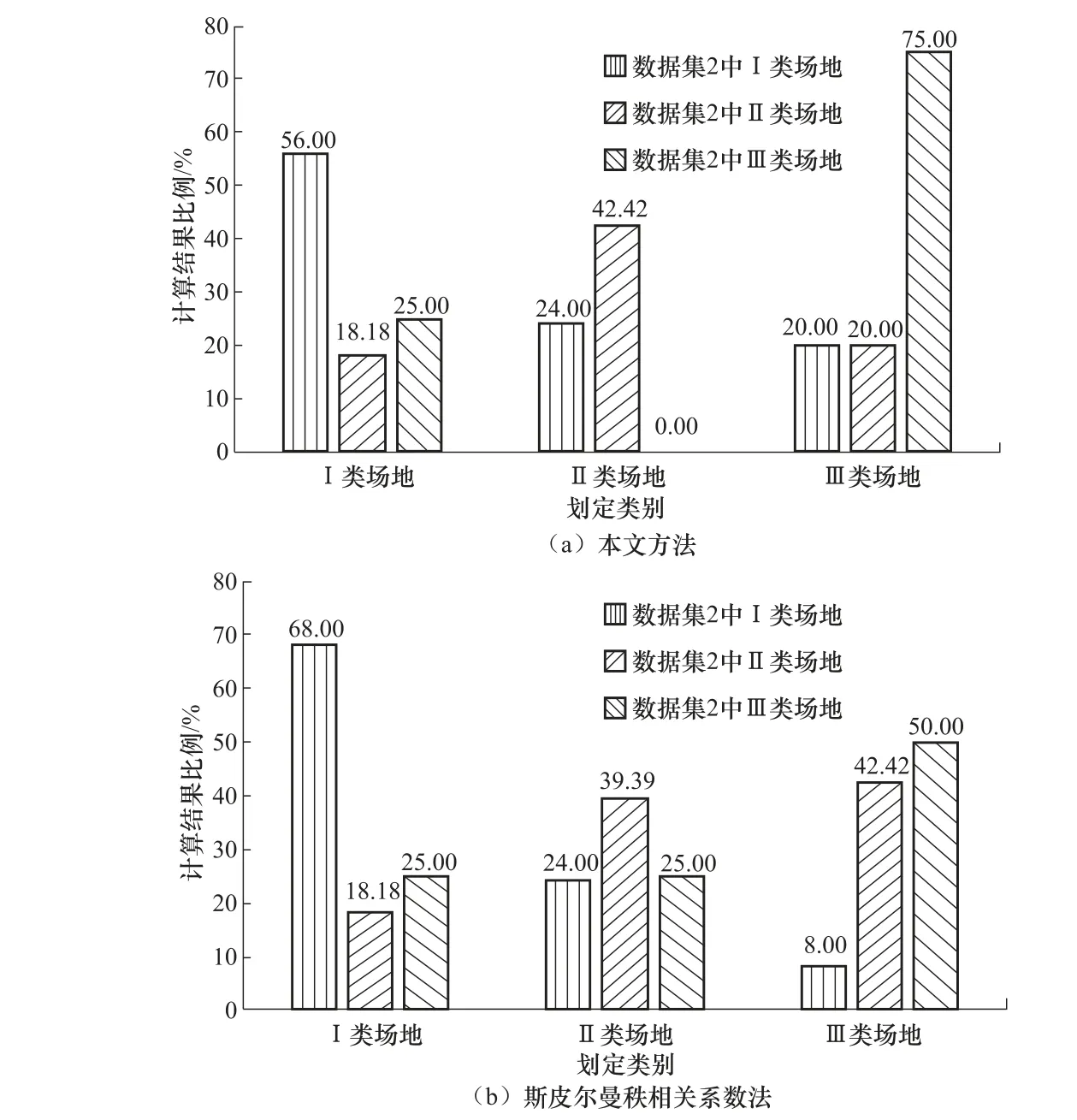
圖5 2 種方法劃分成功率及誤判率 Fig.5 Success rates and failure rates of two classification methods

3.3 分類后譜比曲線

為從側面驗證本文方法的合理性，給出劃分場地類別后的3 條平均曲線，并給出相應的自然對數標準差曲線，與由數據集1 得到的3 條標準譜比曲線對比，結果如圖6 所示。

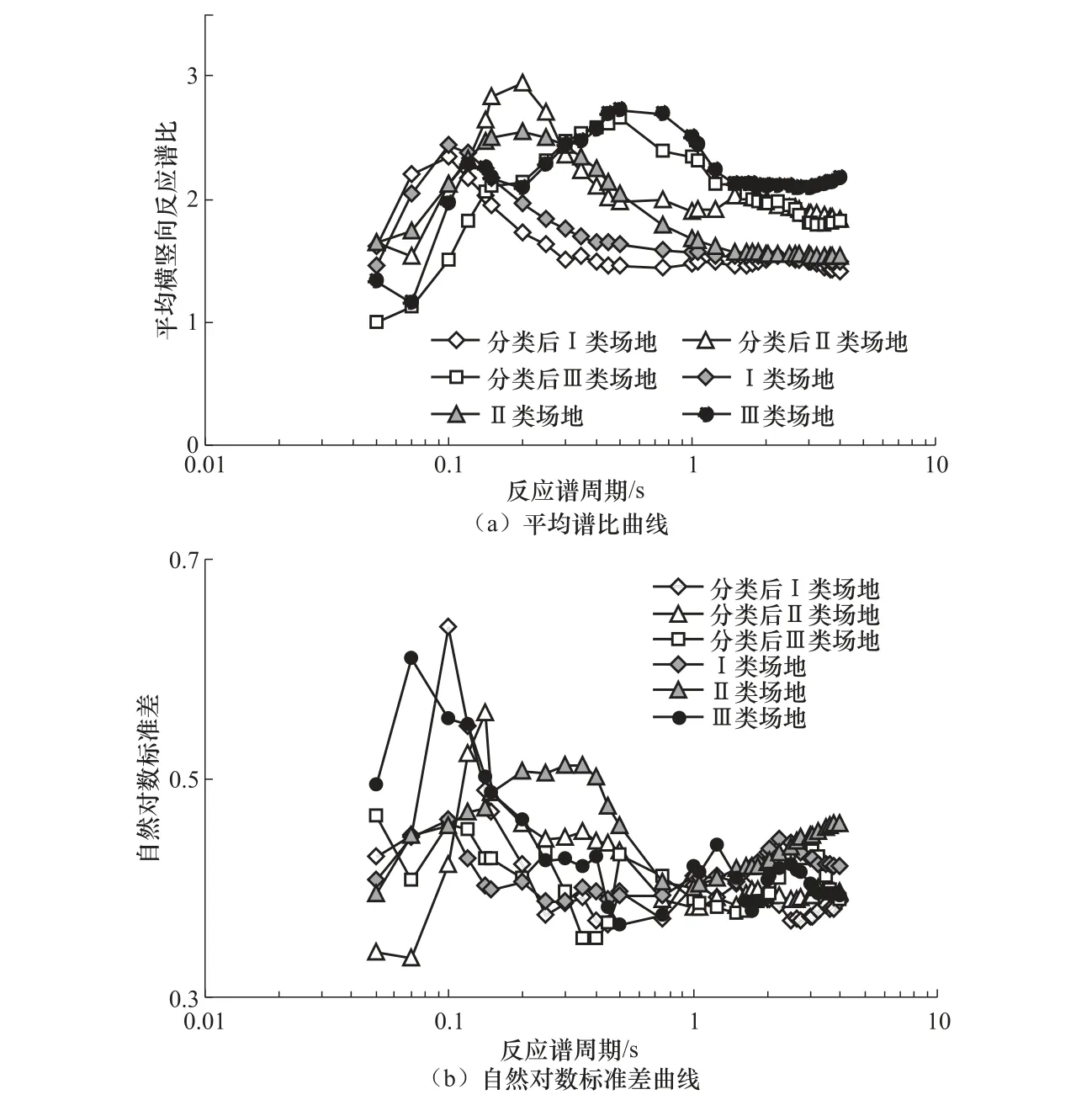
圖6 分類前后3 類場地平均譜比曲線及其自然對數標準差曲線 Fig.6 Standard spectra ratio curves and natural logarithmic standard deviation before and after classification for three site classes

為從側面驗證本文方法的合理性，給出對數據集2 劃分場地類別后的3 條平均譜比曲線及相應的自然對數標準差曲線，并與由數據集1 得到的3 條標準譜比曲線對比，結果如圖6所示。

由圖6（a）可知，經本文方法分類后的I 類場地平均譜比曲線峰值和峰值周期與標準譜比曲線基本接近，0.1s 后I 類場地標準譜比曲線的值略大，但二者下降趨勢基本一致。由圖6（b）可知，分類后的I 類場地自然對數標準差在0.1s 即峰值周期附近和3s 后較大，在其他周期段與標準譜比曲線較為接近。由圖6（a）可知，分類后的II 類場地平均譜比曲線在峰值區（0.1s）前與II 類場地標準譜比曲線基本接近，在峰值區附近及其后的下降段則大于II 類場地標準譜比曲線，但總體形狀相似。分類后的II 類場地自然對數標準差在峰值區附近大于II類場地標準譜比曲線，而其在他周期段上則比II 類場地標準譜比曲線小，如圖6（b）所示。對于III 類場地，由圖6（a）可知，分類后的場地平均譜比曲線僅在某些周期段上較大，而其他周期段則與場地標準譜比曲線基本一致；由圖6（b）可知，0.3s 前，分類后的場地自然對數標準差較大，其他周期則二者接近。

由圖6 可知，使用本文方法分類后，各類場地平均反應譜比曲線與按照鉆孔信息進行場地分類得到的標準譜比曲線基本吻合。數據集2 重新分類后的平均譜比曲線及其自然對數標準差較數據集1 所得結果略有提高，但總體趨勢一致，從側面說明本文所提分類方法的合理性。

4 結論

本文利用收集到的664 個日本KiK-net 臺站場地信息，按照《建筑抗震設計規范（GB 50011—2010）》進行場地分類，以此為基礎構建2 個數據集，進而基于離散Fréchet 距離對數據集2 的場地進行分類，并對分類結果進行校驗，得出以下結論：

（1）按照我國建筑抗震設計規范對KiK-net 臺站進行場地分類，并以此為基礎得到的3類場地標準反應譜比曲線在I、II、III 類場地間具有明顯的區分度。

（2）使用本文所提基于離散Fréchet 距離的方法對強震臺站場地進行分類，分類成功率與誤判率表明該方法具有較高的準確性和可行性。

（3）將本文方法與斯皮爾曼秩相關系數法得到的強震臺站場地分類結果進行比較，結合本文方法得到的平均譜比曲線，表明本文分類方法具有一定合理性。