數(shù)理結(jié)合的賽題典例
——第35屆全國中學(xué)生物理競賽預(yù)賽第6題的4種解法
鐘云杰 柏露枝
(江蘇省常州市北郊高級中學(xué),江蘇 常州 213031)
填空題:田徑場上某同學(xué)將一鉛球以初速度v0拋出,該鉛球拋出點的高度為H.鉛球在田徑場上的落點與鉛球拋出點的最大水平距離為________,對應(yīng)的拋射角θ為________.重力加速度為g.
1 命題意圖研判
數(shù)學(xué)知識既是解決物理問題的工具,更是物理學(xué)發(fā)展的支撐和保障.應(yīng)用數(shù)學(xué)知識解決物理問題的能力既是高考考查學(xué)生物理能力之一,也是全國中學(xué)生物理競賽考查學(xué)生解決物理問題能力水平的重要內(nèi)容之一.第35屆全國中學(xué)生物理競賽預(yù)賽第6題的解法中,蘊含著豐富的數(shù)學(xué)思想和方法,因此,該題的命題意圖旨在通過求斜上拋運動的最大水平射程,凸顯中學(xué)生應(yīng)用數(shù)學(xué)知識解決物理問題的能力水平.現(xiàn)由該題的四種解法展示命題本意.
2 4種解題方法
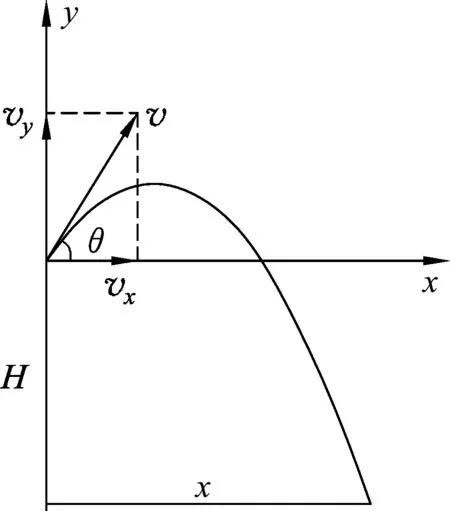
圖1
方法1:分解速度法.
拋體運動常規(guī)的處理方法是,將運動分解為水平方向的勻速直線運動和豎直方向的豎直上拋運動,如圖1所示.由勻速直線運動和豎直上拋運動規(guī)律得
vx=v0cosθ.
(1)
vy=v0sinθ.
(2)
x=vxt.
(3)
(4)
由(1)-(4)式可得
(5)
(5)式可化為
(6)
顯然(6)式是以tanθ為參數(shù)的一元二次方程,因為θ有解,
所以Δ≥0,即
由此解得

解法認(rèn)知:解決拋體運動問題,通常是將拋體運動分解為水平方向和豎直方向兩個分運動來處理.雖然方法1是一種常規(guī)的分解速度法解拋體運動問題,但對學(xué)生的數(shù)學(xué)方程知識、三角函數(shù)知識的應(yīng)用能力有一定的要求.
方法2:分解加速度法.
將加速度分解為與速度方向共線(反向)以及與速度方向垂直兩個方向,如圖2所示.由圖2可知,物體在初速度方向做勻減速直線運動,在垂直初速度方向做初速度為0的勻加速直線運動.
由圖3可見,當(dāng)物體沿初速度方向速度減為0時,物體沿初速度方向位移達(dá)到最大(Q1位置),此時物體到達(dá)地面的實際位置達(dá)到最遠(yuǎn),即Q位置,BQ長度即為所要求的最大射程xm;圖3中∠BAO等于所要求的對應(yīng)拋射角θ.
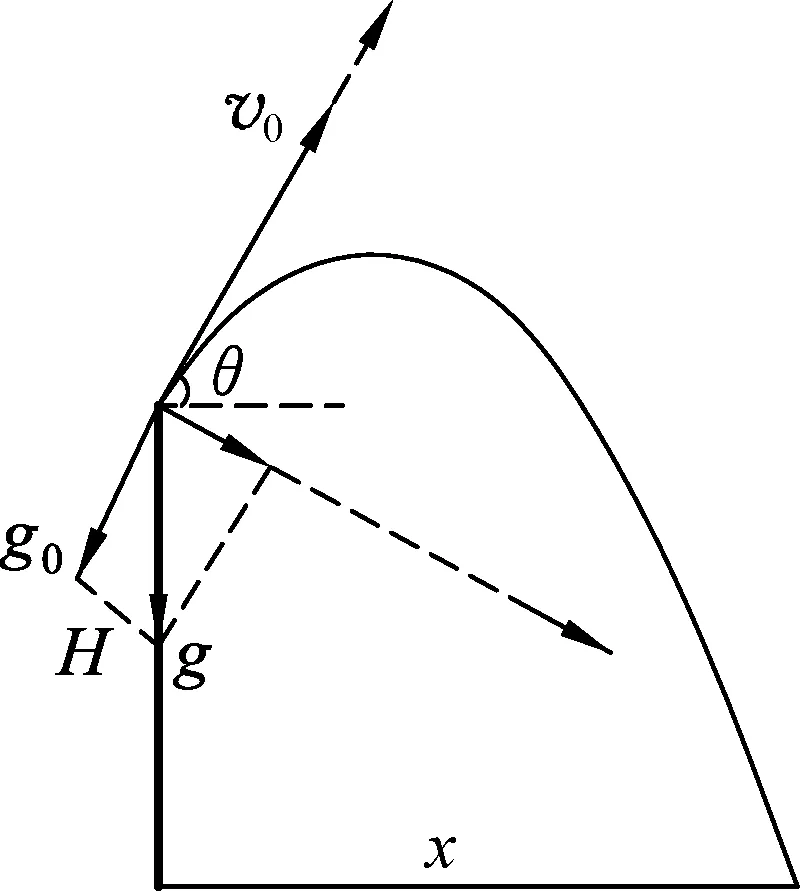
圖2
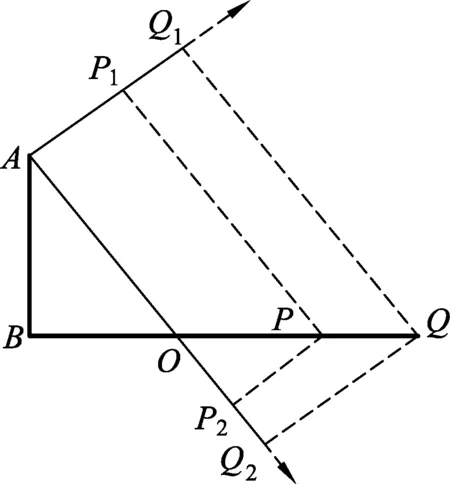
圖3
由加速度分解可得
g0=gsinθ.
(1)
v0方向的最大位移為
(2)
由幾何關(guān)系可知∠BAO=∠Q2QO,故有
(3)
有(1)-(3)式可得
(4)
(4)式由基本不等式規(guī)律可知
即
(5)
將式(5)代入式(4)得
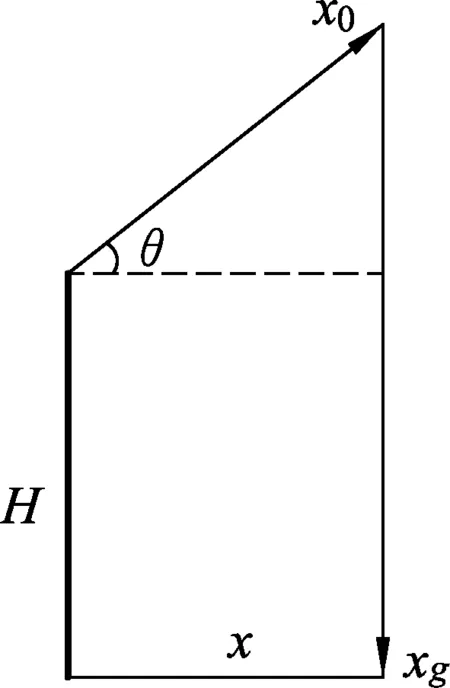
圖4
解法認(rèn)知:運動的分解具有多向性.分解加速度求解拋體運動問題比分解速度求解拋體運動問題在思想層面上突破常規(guī).但分解加速度這種求解方法,對學(xué)生幾何知識和不等式知識的應(yīng)用能力有一定的要求.
方法3:自然分解法.
將物體的運動分解為沿初速度方向的勻速直線運動和豎直方向的自由落體運動,如圖4所示.由此得:
在初速度方向有
x0=v0t.
(1)
在豎直方向有
(2)
由幾何關(guān)系可得
(3)
由式(1)-(3)可得
(4)
(4)式中,將t2作為自變量,可知

(5)
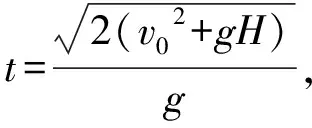
(6)
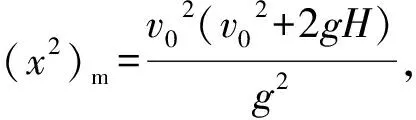
(7)
將式(6)代入式(1)可知
(8)
由于拋射角θ和x0、xm的關(guān)系滿足:
(9)
所以由式(7)-(9)可知
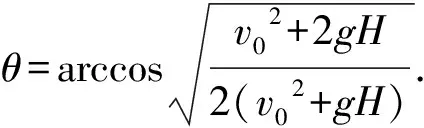
解法認(rèn)知:自然是一種狀態(tài),解題的自然性、本屬性是思維的基本出發(fā)點.基于運動的自然性,拋體運動是初速度方向和豎直方向兩種運動的合運動也就順以為然.顯然從初速度方向的勻速直線運動和豎直方向的自由落體運動求解此題不失為一種基本的、自然的求解方法,但這種解法中凸顯出對一元二次方程和二次函數(shù)知識的靈活應(yīng)用水平.
方法4:動能定理法.
由解法1的圖1可知
vx=v0cosθ.
(1)
x=vxt.
(2)
由式(1)、(2)可得
x=v0tcosθ.
(3)
由于初速度v0確定,即初動能確定;高度也確定,由動能定理可知,末動能確定,即末速度v的大小為定值.那么,由動能定理有
(4)
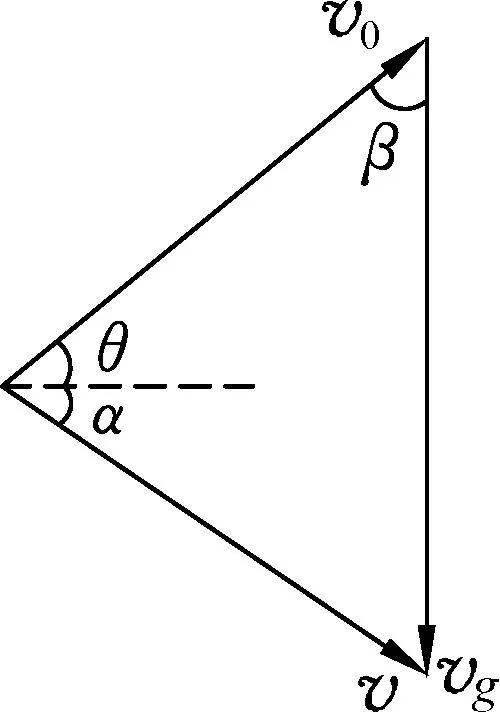
圖5
末速度矢量分解如圖5,易發(fā)現(xiàn)速度矢量三角形面積為
(5)
由式(3)、(5)可得
(6)
而矢量三角形面積又滿足
(7)
由式(6)、(7)可知
(8)
要使x有最大值,則θ+α=90°,結(jié)合(4)后應(yīng)有
拋射角滿足
(9)
由式(4)、(9)可知
解法認(rèn)知:物理知識是解決物理問題之本.動能定理法求解此題,將功能思想融合在純運動問題的解題之中,突破了解決純運動問題的求解域界,實現(xiàn)了思維躍遷.但動能定理法求解此題對學(xué)生向量知識、幾何知識和三角函數(shù)知識的靈活應(yīng)用能力有較高的要求.
綜上可見,該題的4種解法,以運動的合成與分解為主體,以數(shù)學(xué)知識的綜合應(yīng)用為主知,以學(xué)生的數(shù)理結(jié)合能力為主導(dǎo).總之,在這4種解法中,既體現(xiàn)了解決物理問題的自然美和創(chuàng)新美,又體現(xiàn)了物理美和數(shù)學(xué)美在解決物理問題中的結(jié)合美.

