分離窗口快速尺度自適應目標跟蹤算法

楊春德 劉京 瞿中

摘 要：針對核相關濾波器（KCF）跟蹤算法在面對尺度變化時產生的目標漂移問題，提出一種分離窗口快速尺度自適應目標跟蹤算法——FSACF。首先，通過直接對原始幀圖像進行特征提取得到基于顯著性顏色特征的全局梯度組合特征圖，以減小后續的尺度計算對性能的影響;其次，對全局特征圖采用分離窗口法，自適應地選取尺度大小并計算對應的最大響應值;最后，采用定義的置信度函數自適應地更新迭代模板函數，提高模型的魯棒性。通過帶有不同干擾屬性的視頻集上進行實驗，發現FSACF算法與KCF算法相比，在精度上提升7.4個百分點，成功率提高12.8個百分點;與未采用全局特征和分離窗口的算法對比，處理速度上提升1.5倍。實驗結果表明，FSACF算法在尺度變化發生時能有效避免目標漂移的產生，同時具有一定的效率，并在精度與成功率上均優于對比算法。

關鍵詞：目標跟蹤;核相關濾波器;尺度自適應;全局特征;置信度函數

中圖分類號：TP391.41

文獻標志碼：A

文章編號：1001-9081（2019）04-1145-05

Abstract： In order to solve the problem of object drift caused by Kernelized Correlation Filter （KCF） tracking algorithm when scale changes， a Fast Scale Adaptive tracking of Correlation Filter （FSACF） was proposed. Firstly， a global gradient combination feature map based on salient color features was obtained by directly extracting features for the original frame image， reducing the effect of subsequent scale calculation on the performance. Secondly， the method of separating window was performed on the global feature map， adaptively selecting the scale and calculating the corresponding maximum response value. Finally， a defined confidence function was used to adaptively update the iterative template function， improving robustness of the model. Experimental result on video sets with different interference attributes show that compared with KCF algorithm， the accuracy of the FSACF algorithm by was improved 7.4 percentage points， and the success rate was increased by 12.8 percentage points; compared with the algorithm without global feature and separating window， the Frames Per Second was improved by 1.5 times. The experimental results show that the FSACF algorithm avoids the object drift when facing scale change with certain efficiency， and is superior to the comparison algorithms in accuracy and success rate.

Key words： object tracking; Kernelized Correlation Filter （KCF）; scale adaptive; global feature; confidence function

0?引言

目標跟蹤是計算機視覺中最基本的問題之一，在視頻監控[1]、行為分析等方面有著廣泛的應用。盡管目標跟蹤已經取得了較大的進展，但仍受眾多因素的影響，如尺度變化、遮擋[2]等，所以目標跟蹤仍是一個具有挑戰性的課題。

Bolme等[3]提出的最小平方誤差輸出和（Minimum Output Sum of Squared Error， MOSSE）算法，將相關濾波引入跟蹤領域，使跟蹤速度得到提高。而后Henriques等[4]基于MOSSE的框架加入密集采樣的思想提出核循環結構跟蹤（Circulant Structure with Kernel， CSK）算法，利用循環矩陣的性質加速了求解過程。隨后，Henriques等[5]

又對CSK算法加入多通道特征的方法并推導出非線性解，提出非線性核相關濾波器（Kernelized Correlation Filter， KCF）使多特征融合成為可能。Li等[6]針對KCF算法無法處理尺度變化的問題，提出尺度與位移同時計算最優的多特征尺度自適應（Scale Adaptive Multiple Feature， SAMF）跟蹤算法，解決由于尺度變化而導致的目標信息丟失問題，但無法滿足實時性需求，且在面對遮擋時易產生模型污染。

Kalal等[7]提出學習檢測跟蹤（Tracking-Learning-Detection， TLD）算法，將跟蹤和檢測相結合，引入在線學習機制，魯棒性強，具有很強的學習恢復能力，但在面對光照變化等因素影響時易產生目標漂移，并且效率不高。

本文針對KCF算法在尺度變化時易產生漂移的問題，提出一種分離窗口尺度自適應跟蹤算法——FSACF（Fast Scale Adaptive tracking of Correlation Filter）。首先對每幀原始圖像進行全局特征提取，基于顯著性顏色特征和灰度特征提取對應的梯度特征;然后采用提出的尺度自適應算法在全局特征圖上進行計算，以分離窗口的方式選擇合適的尺度進行響應值計算并得到模板函數;最后修改了更新策略，提出一組置信度函數的定義，采用置信度函數對模板函數學習率進行自適應的調整更新，使得模型更加穩定。

1?相關濾波跟蹤算法

相關濾波器跟蹤算法的主要框架包括：首先濾波器采用嶺回歸模型對第一幀選定的目標進行訓練;然后將模型與下一幀的圖像進行快速檢測，通過相關運算得到響應矩陣來確定當前幀圖像中目標的中心位置;最后以新的位置信息對圖像的目標重采樣進行模型更新迭代，重復以上過程實現跟蹤。

1.1?嶺回歸模型建立

假定訓練集的圖像樣本表示為z（mi，ni），則訓練的目標就是找到一個函數f（z）=pTz，使得誤差函數minp（f（z）-Y）2+λ‖p‖2最小。其中：Y為回歸目標;λ為正則化參數，防止過擬合。

為了讓檢測器有更好的表現，Henriques等[5]利用循環矩陣的性質，

其中：zx表示在傅里葉域中z自身的核相關性，是標準正太分布的傅里葉變換。這樣對p的求解就轉變到對偶空間中對α的求解。

1.2?快速檢測運算

循環矩陣的性質同樣被用到了檢測過程中。對下一幀歷史位置提取的圖像塊z進行循環采樣，可以由式（3）得到頻域中的響應函數：

得到響應值矩陣后進行傅里葉逆變換即可得到時域中響應值矩陣，其最大值的位置就是對應目標的中心位置。

2?快速尺度自適應目標跟蹤算法

在目標確定后，本文算法（FSACF）對目標原始圖提取顯著顏色梯度全局特征圖，以避免多次重復提取特征，并提出一種特征組合方式;然后在全局特征圖上采用分離窗口快速尺度估計算法得到響應矩陣，進一步加速尺度信息確定的計算;最后針對響應矩陣的數值進行分析，并代入到提出的置信度函數中，實現對模板函數自適應更新。

2.1?全局特征圖

在相關方法中，傅里葉變換的計算次數與特征維數呈線性關系，為提高計算的速度，本文提出在原始圖的基礎上只進行一次特征提取得到全局特征圖，避免多次提取的重復操作。適當的特征組合也可以顯著地提高檢測性能，而梯度和顏色特征的聯合已被證實有著很強的互補性，但如何進行合適的組合仍是一個有待解決的問題。

常規的方向梯度直方圖（Histogram of Oriented Gradients， HOG）特征[8]和顏色名稱（Color Name， CN）特征[9]的融合是直接相連的，而在不同的顏色空間中，目標的梯度特征是不同的，因此從每個顏色空間中提取梯度特征是一種更好的策略。為了平衡性能，本文提出一種基于顯著性顏色特征提取梯度特征的方法，其過程如下：首先將RGB圖像轉換為11維顏色空間，接著對其降維，提取顯著性顏色特征圖;然后在顯著性顏色特征圖的每一個通道和灰度特征圖上提取HOG特征;最后將得到的梯度特征降維，連接成一個共54通道的三維矩陣為全局特征圖，如圖1所示，后續尺度估計算法直接在全局特征圖上提取對應的目標進行計算。

2.2?快速自適應尺度

如圖2所示：圖2（a）為初始化狀態，圖2（b）～（d）為后續視頻序列根據分離規則分離后得到的對應窗口位置，其中黑點處為當前最大響應值的位置。

當圖2（a）中最大響應處于上半部分時，圖2（b）中w1～wmid-1窗口上移;

當圖2（b）中最大響應處于上半部分時，圖2（c）中w1～wmid-1窗口上移;

當圖2（c）中最大響應處于下半部分時，圖2（d）中w1～wmid-1窗口重新初始化，wmid-1～wm窗口下移。

分離規則如表1所示。表1中：cur表示當前幀最大響應所在的窗口位置;move-1和move+1分別表示對應窗口上移/下移一個單位;stay表示維持當前位置;initialise表示重新初始化到原始位置。

采用分離窗口法可以根據上一幀得到的尺度信息，快速尋找到最適合下一幀目標特征圖feature_map的最可能的m個尺度信息。如圖2（b）所示，當上一幀cur指向hmid-1時，下一幀繼續縮小或保持的概率更大，所以縮小窗口上移偏向選擇縮放比例更小的尺度;而由實驗分析可得，視頻中尺度是漸變的，若此時放大部分的上一尺度不是保持部分則將放大部分初始化至原始位置，保證目標的下一幀目標若為放大時有更適合的尺度與之匹配。

按對應的尺度hisH為大小在feature_map上截取對應尺度特征圖，將得到包含不同比例的正負樣本信息的特征圖，采用雙線性插值法還原到初始尺度，然后將其映射到核空間，代入到式（5），則可以得到目標第t與t-1幀對應的高斯核函數;代入到式（3），則可得到最大響應值，即可確認位置信息和尺度信息。

2.3?自適應更新策略

由于視頻序列的連續性，幀間的目標信息重復性大，大多數跟蹤算法采用的是持續地對模板函數式（2）進行恒定更新迭代，導致跟蹤過程中不可避免的存在模型污染、目標漂移等問題。

經研究發現持續地對模板函數進行更新，在遮擋等情況發生的情況下，不適合的更新容易導致模型污染。針對這個問題，本文提出了一個置信度函數Φ（·），如式（6）所示：

若發生遮擋，為避免采集到過多的錯誤信息污染模型，自適應地調整學習率。

當響應值小于門限μ時，采用αmax3函數降低學習率，降低錯誤采樣對模型造成的影響;當響應值大于門限μ時，采用（αmax-μ）1/4函數，適當地提高更新學習率，維護模型的穩定性。

設new和pre分別表示當前幀和前一幀的模板信息，ξ表示模板函數的學習率，xnew和xpre分別表示當前幀和前一幀的目標信息，η表示目標特征的學習率，hc表示當前幀的尺度信息。根據提出的置信度函數對模板更新函數進行改進，可以得到學習率自適應更新函數如式（7）所示：

對x′目標信息保持持續更新的策略。對于模板函數加入自適應學習率，即控制模板函數在可能發生模型污染的情況下，對模板函數以自適應學習率進行選擇性更新，避免模型污染。對于尺度模板sH逐幀進行更新，以t-1幀時的尺度信息作為第t幀的尺度模板。

2.4?算法流程

FSACF算法的具體流程為：

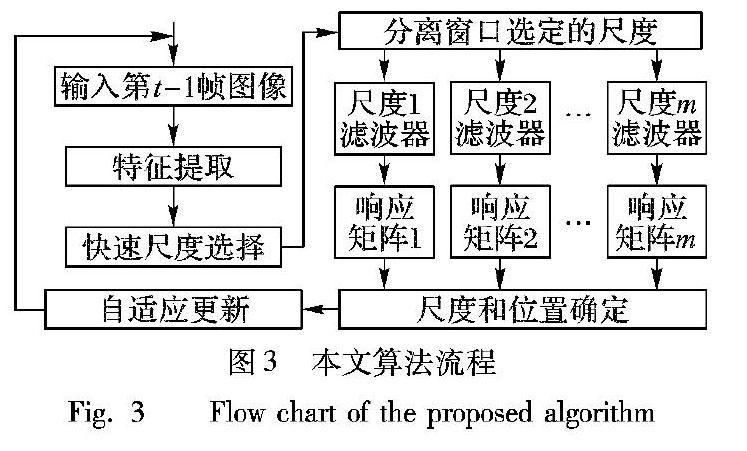
首先輸入第t-1幀的目標中心位置和目標尺度信息，訓練檢測器，根據第t-1幀中的目標中心位置，提取當前第t幀的全局特征圖;然后在全局特征圖上執行快速自適應尺度估計算法進行尺度選擇，將選中的尺度池S中對應的尺度在特征圖中提取出目標，代入到響應值函數進行計算;最后在得到的m組響應矩陣中取最大值進行對比，找到全局最大值的位置，即可確定第t幀的目標中心位置和尺度信息，信息確認后執行自適應更新策略對模板函數和目標信息進行更新。

本文算法流程如圖3所示。

具體算法步驟如下：

輸入?第t-1幀目標中心位置和目標尺度信息。

輸出?第t幀目標的目標中心位置和目標尺度信息。

步驟1?提取第t幀的基于顯著性顏色特征的梯度特征得到全局特征圖。

步驟2?采用分離窗口確定的尺度信息和第t-1幀的中心位置信息，對全局特征圖使用式（5）進行目標特征圖提取，并通過核函數式（6）進行融合得到樣本kxx′。

步驟3?將kxx′依次與模板函數α進行相關運算式（3）得到對應響應圖，選擇擁有最大響應值的響應圖，即可確認第t幀中目標的中心位置與目標尺度信息。

步驟4?對第t幀中的更新模板系數、基樣本x和尺度模板sH采用式（7）進行更新。

重復迭代以上步驟，以實現跟蹤。

3?實驗與結果分析

3.1?實驗參數與評價標準

實驗平臺為Windows 10操作系統，處理器Core i5-6200U，8GB內存，運行平臺為Matlab。實驗測試視頻數據為OTB-50[10]，選取其中40組視頻，涉及到灰度圖像和彩色圖像，同時包含尺度變化、遮擋等11個屬性，每個視頻序列包含多個屬性。為方便與KCF算法進行對比，實驗中參數與KCF算法保持一致。本文為保證精度窗口規模m=5;尺度池S規模t=9，間隔為0.015;學習率ξ=0.01;超參數門限μ=0.25為實驗經驗值。選取了CSK、SAMF等5種算法和本文算法的結果進行定性定量的分析。

所有的實驗均采用四個評價指標：1）精度曲線。精度曲線表示某一距離閾值的正確跟蹤幀的百分比，如果預測的目標中心在距離標準值的一定閾值內，則被認為正確跟蹤，較高的低閾值精度表示跟蹤器更精確，在此選擇的閾值為20個像素。2）平均中心位置誤差（Centre Location Error， CLE）。中心位置誤差是跟蹤算法計算的位置中心與數據集的標準值之間的差異，誤差越小效果越優。3）成功率曲線。成功率是以目標邊界框的重疊率O=|Bt∩Bg|/|Bt∪Bg|進行計算的，其中∩和∪分別表示兩個區域的交集和并集，|·|指的是區域內的像素點個數，Bt為跟蹤的邊界框，Bg是標準邊界框。重疊率越高越準確，這里選擇重疊率的閾值為0.5。4）每秒處理的幀數（Frames Per Second， FPS）。FPS的數值越大說明處理速度越快。

3.2?實驗結果分析

為了評估本文提出的FSACF算法的有效性，選取OTB視頻集中40組視頻，平均所有屬性下的跟蹤結果，繪制出精度曲線和成功率曲線如圖4所示，對比算法包括SAMF、KCF、TLD、核結構化輸出跟蹤算法Struck（structured output tracking with kernels）[11]和CSK算法。

從圖4可看出：本文提出的跟蹤器在20個像素的位置誤差上精度為82.7%，在50%的重疊率上的成功率表現為76.2%，在精確性和魯棒性方面都有很好的應用前景。本文FSACF算法與SAMF算法相比，在精度上高出1.4個百分點，成功率高出3.9個百分點;與KCF算法相比，在精度上提高7.4個百分點，成功率提高12.8個百分點;與Struck算法相比，在精度上高出12.4個百分點，成功率高出18個百分點，在精度與成功率上均優于其他對比算法。由此可以看出，顯著性顏色梯度特征能在一定程度上抑制背景的干擾，經改進后算法對目標信息的捕捉能力有一定提升。

為了驗證本文提出的基于顯著性顏色特征的全局梯度特征法和分離窗口法對尺度計算效率的提升，將FSACF算法與尺度自適應跟蹤（Scale Adaptive Correlation Filter， SACF）算法即無分離窗口和全局特征法的FSACF算法進行比較。本文提出的FSACF算法在處理速度方面如表2所示（這里只選擇了部分的視頻序列進行列舉），平均比SACF算法提升1.5倍。

對超參數μ進行對比分析實驗如圖5所示，其中μ分別取值0～0.7（以0.05為間隔）。以不同μ值依次對FSACF算法進行測試，得到的精度取平均值，可以從實驗結果中看出在μ=0.25時可以得到最高成功率。當給置信度函數選取適當的μ值，模型在一定程度上可以避免異常值對模型造成的污染，從而緩解因遮擋等因素而引起的目標漂移問題。

選取多組視頻序列進行定性分析，各算法的跟蹤結果如圖6所示。實驗結果顯示，現有的一些跟蹤算法僅能在自然場景中小部分干擾因素下正常跟蹤，當有光照、尺度等因素影響時效果反差大，易產生目標漂移等問題。

而FSACF算法采用顏色梯度特征能很好地克服光照變化的影響， 同時采用了分離窗口法有效地克服了尺度變化對跟蹤造成的影響。

當尺度發生較大變化時FSACF算法在三組視頻中均能準確地框定出目標，其他算法則易產生不同程度的目標漂移。所以FSACF算法具有良好的魯棒性，特別是在尺度變化方面表現優異。

4?結語

針對KCF算法在跟蹤過程中面對尺度變化和遮擋發生時易產生目標漂移和模型污染的問題，對其進行改進，提出FSACF算法。本文利用顏色空間和梯度特征的互補性，提出的全局組合特征和分離窗口法，不但能處理尺度的問題，同時保證了實時性的需求。并驗證了置信度函數可以在一定程度上提高模型更新策略的魯棒性，避免模型污染。但綜合所有干擾因素的情況，整體跟蹤精度與成功率沒有大幅度的提升。在接下來的工作中，如何在保證效率的同時對精度與成功率進行進一步的提升是下一步的研究重點。

參考文獻（References）

[1] ZHENG Y， LI S E， WANG J， et al. Stability and scalability of homogeneous vehicular platoon： study on the influence of information flow topologies [J]. IEEE Transactions on Intelligent Transportation Systems， 2016， 17（1）： 14-26.

[2] 勾承甫， 陳斌， 趙雪專， 等. 基于隨機一致性采樣估計的目標跟蹤算法 [J]. 計算機應用， 2017， 36（9）： 2566-2569. （GOU C F， CHEN B， ZHAO X Z， et al. Object tracking algorithm based on random sampling consensus estimation [J]. Journal of Computer Applications， 2017， 36（9）： 2566-2569.）

[3] BOLME D S， BEVERIDGE J R， DRAPER B A， et al. Visual object tracking using adaptive correlation filters [C]// CVPR 2010： Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. ?Washington， DC： IEEE Computer Society， 2010： 2544-2550.

[4] HENRIQUES J F， RUI C， MARTINS P， et al. Exploiting the circulant structure of tracking-by-detection with kernels [C]// ECCV 2012： Proceedings of the 12th European Conference on Computer Vision， LNCS 7575. Berlin： Springer， 2012： 702-715.

[5] HENRIQUES J F， CASEIRO R， MARTINS P， et al. High-speed tracking with kernelized correlation filters [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2015， 37（3）： 583-596.

[6] LI Y， ZHU J. A scale adaptive kernel correlation filter tracker with feature integration [C]// ECCV 2014： Proceedings of the 2014 European Conference on Computer Vision， LNCS 8926. Berlin： Springer， 2014： 254-265.

[7] KALAL Z， MATAS J. Tracking learning detection [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2012， 34（7）： 1409-1422.

[8] FELZENSZWALB P， GIRSHICK R， MCALLESTER D， et al. Object detection with discriminatively trained part-based models [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2010， 32（9）： 1627-1645.

[9] DANELLJAN M， KHAN F S， FELSBERG M， et al. Adaptive color attributes for real-time visual tracking [C]// CVPR 2014： Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition. ?Washington， DC： IEEE Computer Society， 2014： 1090-1097.

[10] WU Y， LIM J， YANG M H. Object tracking benchmark[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2015， 37（9）： 1834-1848.

[11] HARE S， GOLODETZ S， SAFFARI A. Struck： structured output tracking with kernels[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2016， 38（10）： 2096-2109.