中學(xué)數(shù)學(xué)中的無(wú)窮級(jí)數(shù)問(wèn)題*

☉廣東省佛山市順德區(qū)廣東碧桂園學(xué)校 李傳洲

☉武漢晴川學(xué)院計(jì)算機(jī)學(xué)院 楊 艷

一、前言

合情推理是數(shù)學(xué)里面非常重要的推理方法，它包含歸納和類比兩種推理方法，在數(shù)學(xué)研究中，合情推理常常能幫助我們猜測(cè)并發(fā)現(xiàn)一個(gè)新結(jié)論；在證明一個(gè)數(shù)學(xué)結(jié)論之前，合情推理常常能為我們提供證明的思路和方向.法國(guó)數(shù)學(xué)家拉普拉斯（Laplace，1749-1827）曾經(jīng)說(shuō)過(guò)：“即使在數(shù)學(xué)里，發(fā)現(xiàn)真理的主要工具也是歸納和類比.”

但是合情推理所得的結(jié)論是需要證明的，這正是數(shù)學(xué)區(qū)別于其他學(xué)科的顯著特點(diǎn).美籍匈牙利數(shù)學(xué)家喬治·波利亞（1887-1985）說(shuō)過(guò)：“合情推理是冒險(xiǎn)的、有爭(zhēng)議的和暫時(shí)的.”合情推理所獲的結(jié)論，僅僅是一種猜想，未必可靠.例如，法國(guó)數(shù)學(xué)家費(fèi)馬觀察到

221+1=5，

222+1=17，

223+1=257，

224+1=65537

都是質(zhì)數(shù)，于是他用歸納推理提出猜想：任何形如22n+1（n∈N*）的數(shù)都是質(zhì)數(shù).這就是著名的費(fèi)馬猜想.半個(gè)世紀(jì)后，善于計(jì)算的歐拉（Euler）發(fā)現(xiàn)，第5個(gè)費(fèi)馬數(shù)

F5=225+1=4294967297=641×6700417

不是質(zhì)數(shù)，從而推翻了費(fèi)馬的猜想.

在中學(xué)數(shù)學(xué)的教學(xué)中，類比和歸納的推理方法有著廣泛的應(yīng)用，如數(shù)學(xué)歸納法、立體幾何與平面幾何的類比、向量與數(shù)的類比、無(wú)限與有限的類比等等.本文將著重討論中學(xué)數(shù)學(xué)的實(shí)際教學(xué)中無(wú)限與有限類比時(shí)所產(chǎn)生的問(wèn)題與困惑，以及如何利用無(wú)窮級(jí)數(shù)來(lái)解決所產(chǎn)生的問(wèn)題.

二、無(wú)限求和與無(wú)窮級(jí)數(shù)

在學(xué)習(xí)有理數(shù)概念的時(shí)候，我們需要討論無(wú)限循環(huán)小數(shù)是否是有理數(shù)，關(guān)鍵在于無(wú)限循環(huán)小數(shù)能否轉(zhuǎn)化為分?jǐn)?shù)形式.如0.134513451345…能否轉(zhuǎn)化為分?jǐn)?shù)？中學(xué)或小學(xué)階段老師所教的將循環(huán)小數(shù)化為分?jǐn)?shù)的方法如下：

問(wèn)題1：如何將0.134513451345…化為分?jǐn)?shù)？

解：假設(shè)x=0.134513451345…

則10000x=1345.134513451345…

將兩個(gè)等式相減得9999x=1345

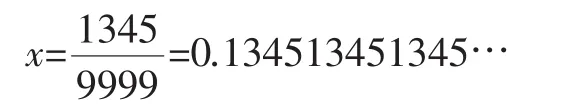
上述方法中讓10000x與x的無(wú)限小數(shù)部分抵消了，思考這樣做是否合理？

受到這個(gè)問(wèn)題的啟發(fā)，有很多學(xué)生又提出了新的問(wèn)題，問(wèn)題如下：

問(wèn)題2：“令S＝1+2+4+8+…，則2S＝2+4+8+…，那么S-2S＝1.”到底S與2S誰(shuí)大？

上述兩個(gè)問(wèn)題在計(jì)算時(shí)用到了同樣的方法，但第二個(gè)卻出現(xiàn)了矛盾，這是為什么呢？如果老師不能合理地解釋這兩個(gè)問(wèn)題，想必在學(xué)生心中教師的權(quán)威也會(huì)降低不少吧.

本質(zhì)上，上面兩個(gè)問(wèn)題都可以看成是無(wú)窮級(jí)數(shù)的問(wèn)題.在中小學(xué)階段，由于所學(xué)知識(shí)有限，只進(jìn)行有限求和運(yùn)算，而對(duì)于無(wú)限求和當(dāng)然是不涉及的.數(shù)學(xué)是嚴(yán)謹(jǐn)?shù)模蓡?wèn)題2可知，有限求和法則不一定適合無(wú)限求和的運(yùn)算，那么我們應(yīng)該如何處理無(wú)限求和運(yùn)算呢？本文關(guān)于無(wú)限求和運(yùn)算的討論主要針對(duì)上述兩個(gè)簡(jiǎn)單的問(wèn)題.

定義1：給定一個(gè)數(shù)列{un}，對(duì)它的各項(xiàng)依次用“+”號(hào)連接起來(lái)的表達(dá)式

稱為數(shù)項(xiàng)級(jí)數(shù)或無(wú)窮級(jí)數(shù)（常簡(jiǎn)稱為級(jí)數(shù)），其中un稱為數(shù)項(xiàng)級(jí)數(shù)（1）的通項(xiàng).

數(shù)項(xiàng)級(jí)數(shù)（1）也常寫作：或簡(jiǎn)寫為∑un.

數(shù)項(xiàng)級(jí)數(shù)（1）的前n項(xiàng)和，記為

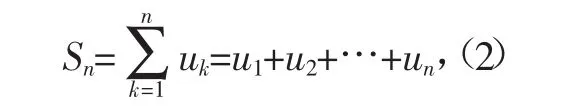
稱它為數(shù)項(xiàng)級(jí)數(shù)（1）的第n個(gè)部分和，也簡(jiǎn)稱為部分和.

定義2：若數(shù)項(xiàng)級(jí)數(shù)（1）的部分和數(shù)列{Sn}收斂于S（即limSn=S），則稱數(shù)項(xiàng)級(jí)數(shù)（1）收斂，稱S為數(shù)項(xiàng)級(jí)數(shù)（1）n→∞的和，記作S=u1+u2+…+un+…或S=∑un.

若{Sn}是發(fā)散的，則數(shù)項(xiàng)級(jí)數(shù)（1）發(fā)散.

例1討論等比級(jí)數(shù)（也稱為幾何級(jí)數(shù)）

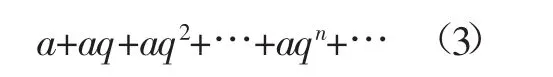
的收斂性，其中|q|＜1，a≠0.

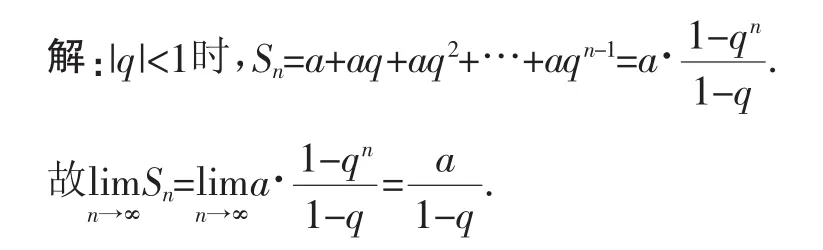
回到問(wèn)題1，可以將0.134513451345…寫成無(wú)窮級(jí)數(shù)的形式，

0.134513451345…=0.1345+0.1345×10-4+0.1345×10-8+…+0.1345×10-4n+…

由例1可知，這是一個(gè)等比級(jí)數(shù)，其中a=0.1345，q=10-4＜1，所以該級(jí)數(shù)收斂且

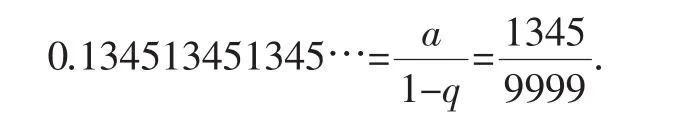
實(shí)際上，對(duì)于更一般的情形，設(shè)一個(gè)含有n（0＜n＜+∞）個(gè)整數(shù)的有限數(shù)列：

B={b1，b2，…，bn}，其中bi∈{1，2，…，9}，（i∈1，2，…，n），

則對(duì)任意一個(gè)循環(huán)節(jié)不含0的純循環(huán)小數(shù)m，均可表示為：

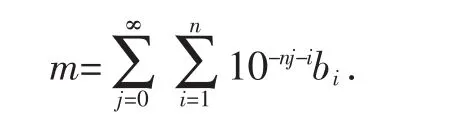
顯然m是一個(gè)收斂的幾何級(jí)數(shù)，由例1可知，

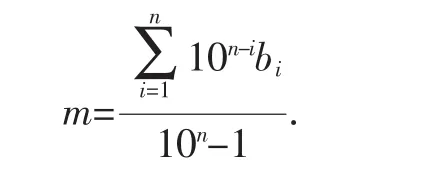
同理可證任意一個(gè)循環(huán)節(jié)含0的純循環(huán)小數(shù)也可化為分?jǐn)?shù)，所以任意的循環(huán)小數(shù)均可化為分?jǐn)?shù).

對(duì)于問(wèn)題2，無(wú)窮級(jí)數(shù)S的前n項(xiàng)和Sn=1+2+…+2n-1→∞（n→+∞）發(fā)散，故無(wú)窮級(jí)數(shù)S不存在和，所以“S-2S=1”的結(jié)論顯然是錯(cuò)的.

我們?cè)倏匆粋€(gè)類似的問(wèn)題：

問(wèn)題3：研究級(jí)數(shù)

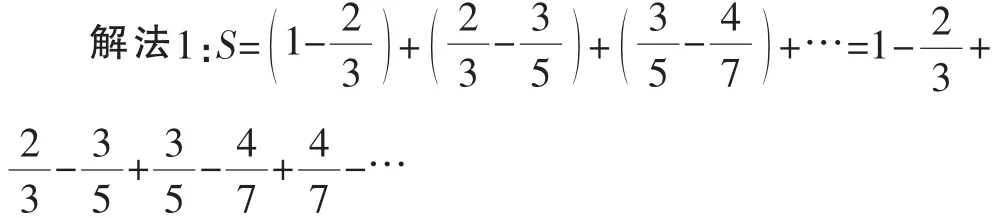
于是，從第二項(xiàng)起全部抵消，故S=1.

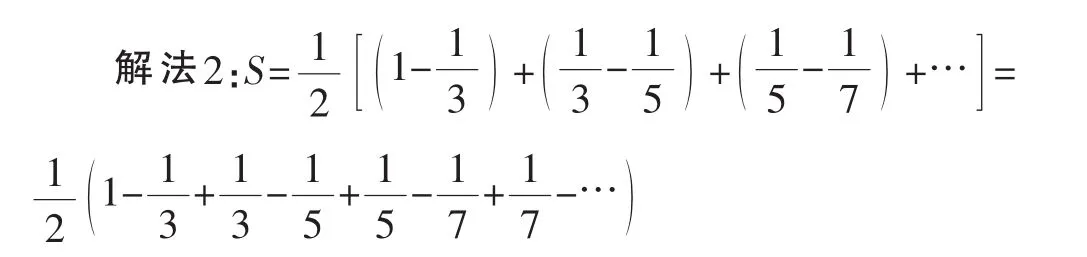
括號(hào)內(nèi)從第二項(xiàng)起全部抵消，故

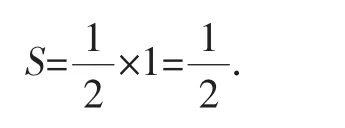
顯然，上述兩種解法的結(jié)果是矛盾的.

對(duì)于上述問(wèn)題中的無(wú)窮級(jí)數(shù)求和問(wèn)題，若不討論其是否收斂隨便求和，企圖用有限求和的計(jì)算法則去處理無(wú)限求和的問(wèn)題，這是不嚴(yán)謹(jǐn)?shù)模⑶胰菀壮霈F(xiàn)錯(cuò)誤的認(rèn)知.實(shí)際上，對(duì)無(wú)窮級(jí)數(shù)的收斂問(wèn)題討論得不深入透徹是引發(fā)第二次數(shù)學(xué)危機(jī)的原因之一，且引起了長(zhǎng)達(dá)百余年的混亂.19世紀(jì)以來(lái)，由于法國(guó)數(shù)學(xué)家達(dá)朗貝爾，德國(guó)數(shù)學(xué)家魏爾斯特拉斯（Weirstrass，1815～1897）和法國(guó)數(shù)學(xué)家柯西（Cauchy，1789～1857）詳細(xì)而系統(tǒng)地提出了極限理論，而后來(lái)由德國(guó)數(shù)學(xué)家戴德金（Dedekind，1831～1916），康托（Cantor，1845～1918）等人完善了實(shí)數(shù)理論，從而結(jié)束了長(zhǎng)達(dá)百余年的混亂，所謂第二次數(shù)學(xué)危機(jī)亦得到解決.

三、結(jié)束語(yǔ)

作為新世紀(jì)的中學(xué)數(shù)學(xué)老師，需打下牢固的數(shù)學(xué)理論基礎(chǔ)，不斷地積累學(xué)習(xí)數(shù)學(xué)知識(shí)和解決數(shù)學(xué)問(wèn)題的經(jīng)驗(yàn)，不能將對(duì)數(shù)學(xué)的認(rèn)識(shí)僅僅停留在經(jīng)驗(yàn)水平上，對(duì)數(shù)學(xué)的起源和發(fā)展以及發(fā)展過(guò)程中的矛盾和斗爭(zhēng)需要有一個(gè)全面的認(rèn)識(shí)，深化并提高對(duì)數(shù)學(xué)具體方法的了解，把握數(shù)學(xué)家的創(chuàng)造所賴以產(chǎn)生的時(shí)代背景以及數(shù)學(xué)家的這些創(chuàng)造對(duì)數(shù)學(xué)發(fā)展的貢獻(xiàn)，自覺(jué)樹立正確的數(shù)學(xué)觀，否則就不能達(dá)到全面貫徹?cái)?shù)學(xué)課程的目標(biāo)，更不能正確的傳播數(shù)學(xué)思想.