反空襲作戰中預警機綜合作戰能力分析

翟海清 吳福初 張 楊

（海軍航空大學 煙臺 264001）

1 引言

反空襲作戰是海軍要地，尤其是島礁要地防御作戰的主要內容之一，具有突發性強、反應時間短、作戰被動和抗擊難度大等特點。由于現代空襲兵力兵器突防速度高，打擊距離遠，從而對目標的遠程預警探測提出了更高的要求。而預警機集預警、指揮、通信、情報和電子干擾等功能于一體，具有較強的戰場感知和信息處理能力，已成為現代反空襲作戰中遂行預警偵察和指揮引導任務的最主要力量，對于發揮防空兵力的作戰效能，贏得反空襲作戰勝利具有舉足輕重的作用［1～4］。由于反空襲作戰環境復雜，影響預警機作戰能力的因素多且難以量化，故采用貝葉斯理論對影響作戰能力的因素進行定性分析和量化處理，利用貝葉斯網絡在解決不確定性問題方面的優勢，構建基于貝葉斯網絡的預警機綜合作戰能力評估模型，并對預警機綜合作戰能力進行了評估。

2 貝葉斯網絡簡述

貝葉斯網絡又稱信念網絡（BeliefNetworks）或因果網絡（CausalNetworks），是描述數據變量之間依賴關系的一種圖形模型，在處理不確定性復雜問題方面具有優勢［5］。通常我們把滿足以下四個條件的有向無環圖稱為貝葉斯網絡［8］：

2）每一個變量的取值既可以是離散的也可以是連續的；

3）由變量對應的節點和節點之間的有向邊構成一個有向無環圖G=V，E ，其中V為節點集，與領域的隨機變量一一對應，E為有向邊集，反應節點變量之間的因果依賴關系；

4）對每個節點 Xi和它的父節點集合Pa（Xi）都對應一個條件概率分布表P(Xi|Pa((Xi))，且滿足

從上面的定義可知，貝葉斯網絡是由一個有向無環圖和若干條件概率表組成，其中前者定性刻畫了變量之間的依賴和獨立關系，而后者則定性地描述了變量節點與其父節點之間的依賴關系。因此，貝葉斯網絡具有較強的模擬現實問題中不同因素間的相互作用關系、解決不確定性問題以及處理殘缺數據的能力［6］。

一般情況下，應用貝葉斯網絡解決實際問題包括以下四個步驟［7］：

1）從實際應用中提取得到相關影響因素的變量，確定它們狀態的可能取值；

2）建立反應這些變量之間關系的有向無環圖；

3）確定反應變量之間關系的條件概率表；

4）利用貝葉斯網絡模型計算出最終結果。

3 預警機綜合作戰能力影響因素分析

反空襲作戰中，預警機主要任務有：一是按作戰需要前出配置于敵主要威脅方向上的指定空域內，對來襲目標實施早期的預警探測；二是在發現目標后，測定目標的位置和運動要素，指揮引導己方防空兵力對敵來襲目標進行攔截；三是根據上級命令，對敵實施電子干擾。所以，根據基于預警機作戰使用的主要作戰任務及相關要求，反空襲作戰中影響預警機綜合作戰能力的因素主要有：預警機持續作戰能力、對空探測能力、指揮引導能力以及電子對抗能力等［8］。

3.1 持續作戰能力

預警機持續作戰能力是保證反空襲作戰中預警機完成各項任務的重要前提，其影響因素主要包括續航時間、完好率和機載工作人員的工作時間等。

3.2 對空探測能力

預警機在預定巡邏空域遂行對空預警探測任務是反空襲作戰中預警機的主要作戰任務之一。對空探測能力的強弱直接影響到預警機預警探測的準確性和預警時效性，是衡量預警機綜合作戰效能的關鍵因素［9］。預警機對空探測能力主要取決于預警機機載雷達探測的強效區寬度、漏警率、有效探測時間和探測距離等因素［10］。

圖1 預警機空中巡邏示意圖

1）強效區寬度的計算

預警機強效區寬度是反應預警機探測范圍的重要指標之一，其計算模型為

式中：D探測為機載雷達探測距離；D近界為發現近界；V敵為敵目標速度；V警為預警機速度；t轉彎為預警機飛離至安全區的時間；R為預警機轉彎半徑；A敵地為敵機載武器最大射程；t轉彎轉為預警機90°轉彎所需時間；L為巡邏邊長；tanα==速度比。

2）漏警率

漏警率是指預警機對已經進入探測范圍內目標的探測概率，其計算模型為

式中：P為漏警率；D航距為目標航線距弱效區外邊界的距離。

3）有效探測時間

預警機有效探測時間是目標進入預警機探測范圍后，預警機對其始終探測、監視的時間，其計算模型為

式中：U為目標航線距巡邏邊長近端距離，tmax為最長有效探測時間；tmin為最短有效探測時間，tˉ為平均有效探測時間。

圖2 有效探測時間示意圖

3.3 指揮引導能力

指揮引導能力是預警機指揮引導己方防空兵力對來襲敵機進行攔截的能力，是影響預警機綜合作戰能力重要的因素，主要包括目標處理能力、引導解算能力和對空通信保障能力。

3.4 電子對抗能力

電子對抗能力是預警機遂行電子對抗任務時所具備的電子攻防能力。由于自身攜帶一定的干擾設備，預警機有時擔負一定的電子對抗的任務，或者利用電子干擾能力在一定程度上保障自身安全。因此，電子干擾能力也是預警機綜合作戰能力的影響因素。預警機電子干擾能力通常包括電子防御能力和電子進攻能力兩個方面。

4 基于貝葉斯網絡的預警機綜合作戰能力評估模型

4.1 預警機綜合作戰能力貝葉斯網絡模型的構建

在上節分析的基礎上，根據各影響因素之間的因果關系，構建出預警機綜合作戰能力評估的貝葉斯網絡有向無環圖，如圖3所示。

圖3 預警機綜合作戰能力評估有向無環圖

模型中變量的狀態集合如下：

預警機綜合能力=［強、中、弱］；持續作戰能力=［強、弱］；對空探測能力=［強、弱］；指揮引導能力=［強、弱］；電子對抗能力=［強、弱］；續航時間=｛長、短｝；完好率=｛高、低｝；工作時間=｛長、短｝；強效區寬度=｛寬、窄｝；漏警率=｛高、低｝；有效探測時間=｛長、短｝；探測距離=｛遠、近｝；目標處理能力=｛強、弱｝；引導解算能力=｛高、低｝；對空通信保障能力=｛強、弱｝；電子防御能力=｛強、中、弱｝；電子進攻能力=｛強、中、弱｝。

4.2 影響預警機作戰能力因素的條件概率模型

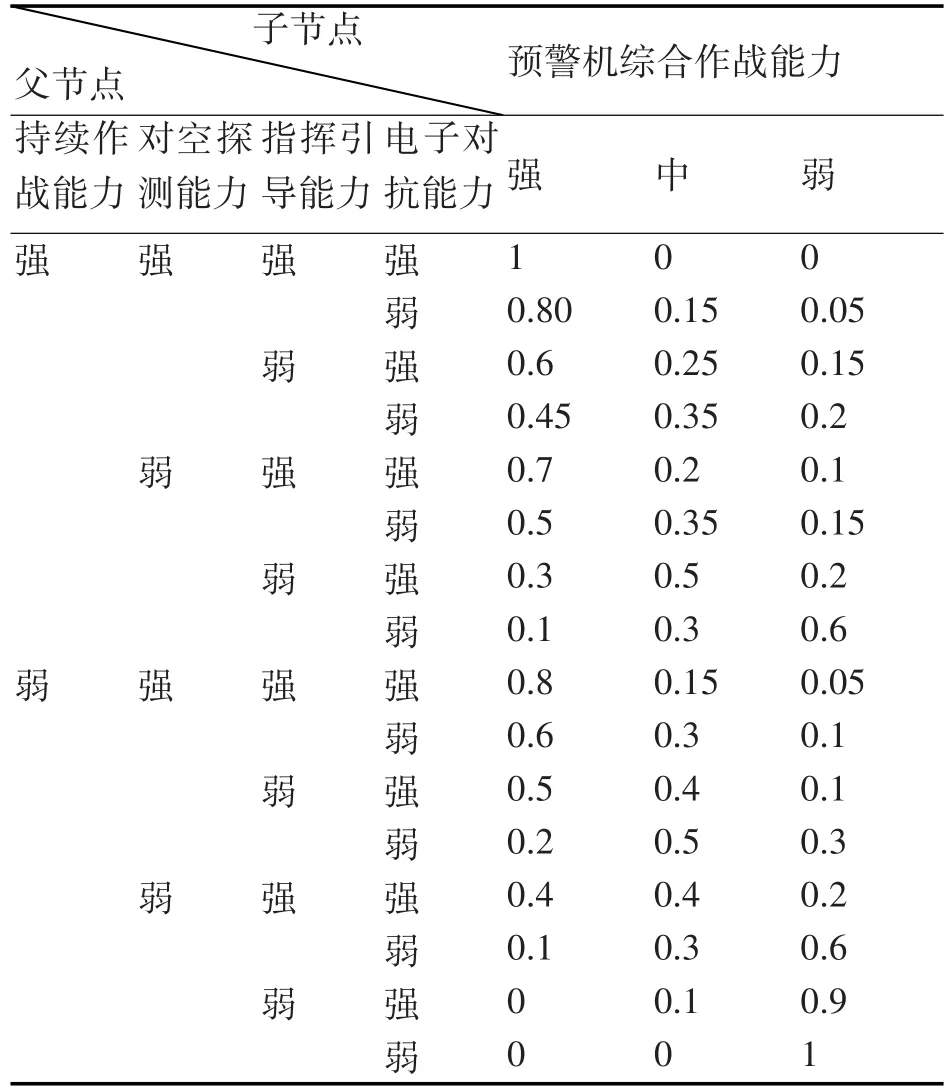
表1 預警機作戰能力評估的條件概率

條件概率矩陣反映的是領域專家對于網絡中關聯節點之間因果關系的看法，是一種專家知識，難免存在一定的主觀性［11］。根據專家經驗得到條件概率如表1。

預警機持續作戰能力、對空探測能力、指揮引導能力以及電子戰能力的強弱等級可以通過各自相關因素確定，如表2～5所示。

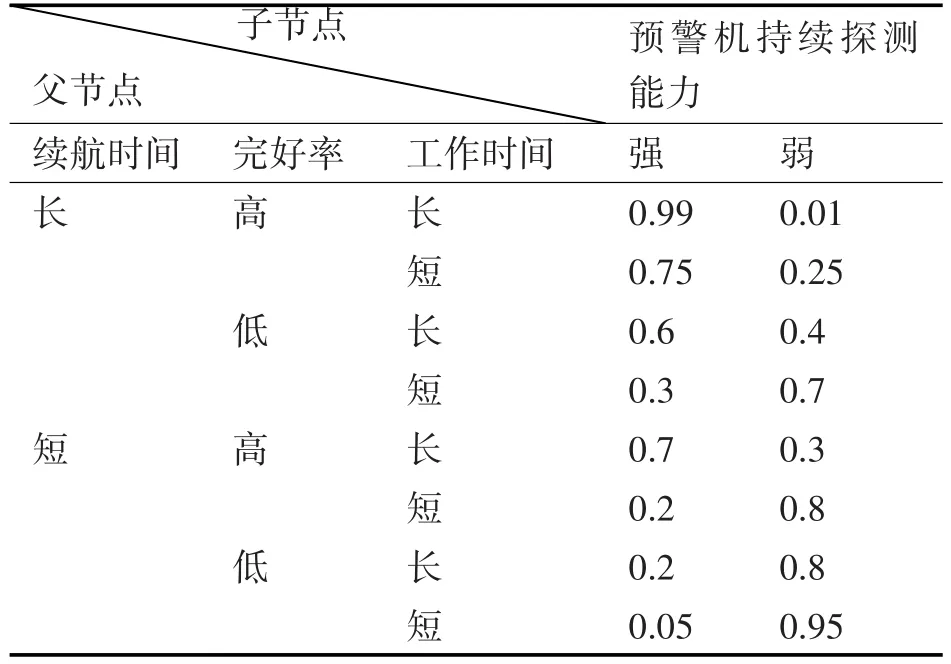
表2 預警機持續作戰能力的條件概率

表3 預警機對空探測能力的條件概率

為減小主觀性對條件概率表的影響，可以采取樣本數據反復調試的方法或根據以往數據庫的數據，對其進行適度的調整，以提高評估結果的可信性。

4.3 隸屬度函數模型

由于影響預警機綜合作戰能力的各因素狀態集合是模糊分類的結果，構建模型的輸入數據是似然概率。對于不確定性因素可采取專家經驗知識打分的方法進行分類，而對于有確定性值的因素則利用隸屬度函數將觀測值轉變為似然概率。若觀測樣本x是包含n個特征的向量，用一系列隸屬度函數的值來表示，即：，隸屬度函數表示為［12］

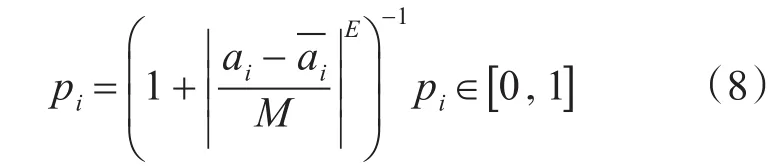
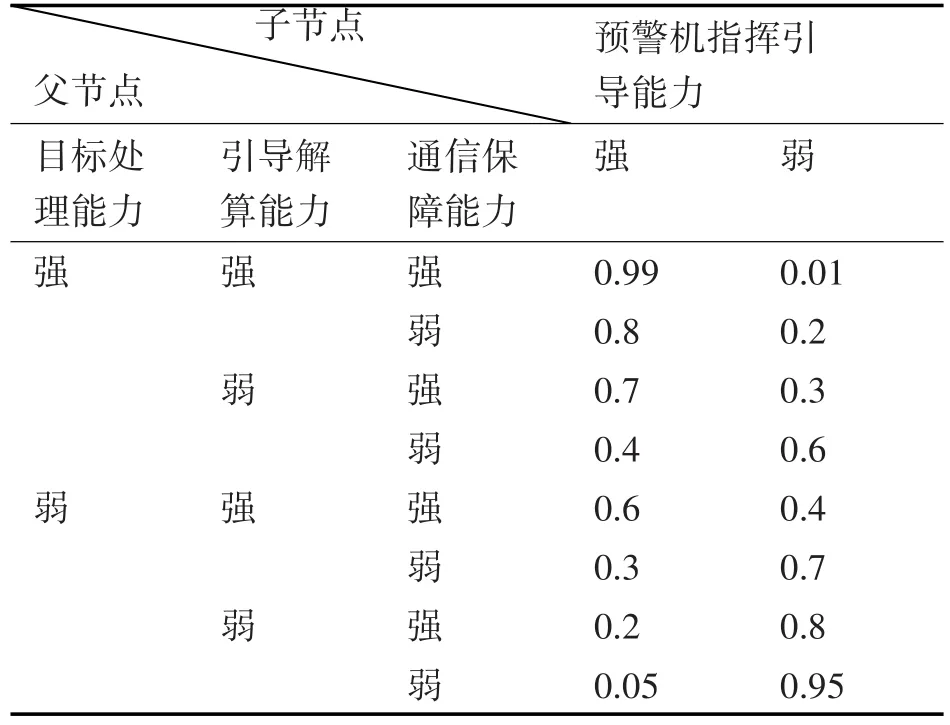
表4 預警機指揮引導能力的條件概率

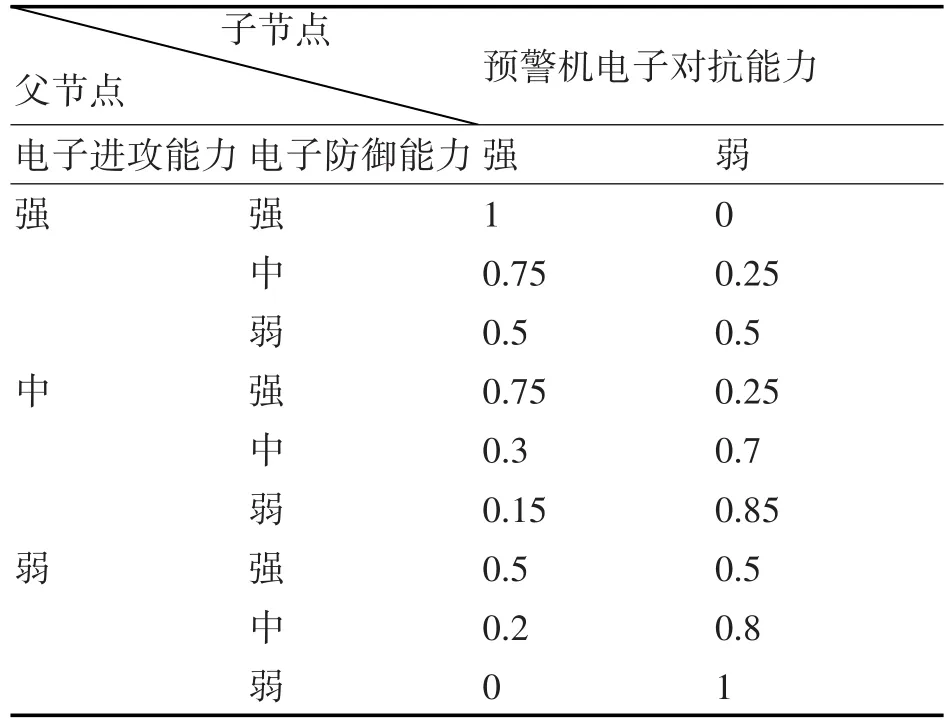
表5 預警機電子對抗能力的條件概率

5 算例分析

當前，貝葉斯網絡構建與實現的工具主要有基于Matlab的貝葉斯網絡工具箱，MSBNX和Netica等軟件［13］。其中，Netica以其建模方便、操作簡單、可視化和適用性強等優點而得到廣泛的運用。

依據預警機作戰使用的特點和Netica軟件的使用要求，本文對預警機綜合作能力量化分析的條件做如下假設：設某預警機續航時間8h，完好率80%，工作時間6h，目標飛行速度900km/h，預警機速度600km/h，預警機飛離至安全區的時間0.5h，預警機轉彎半徑10km，目標武器（對地）最大射程100km，預警機轉90°所需時間10min，目標航線距弱效區外邊界的距離50km，敵機來襲方向偏離巡邏邊長近端距離100km，一次性處理目標批次100批。

將以上條件參數帶入式（1）～（7）中，得到相關因素的量化數值，通過隸屬度函數和以往經驗數據，轉化為似然概率。引導解算能力、對空通信保障能力、電子防御能力以及電子進攻能力等因素不能通過準確的數值計算來確定，可以用過采用專家打分法得到這些子節點的先驗概率，如表6。

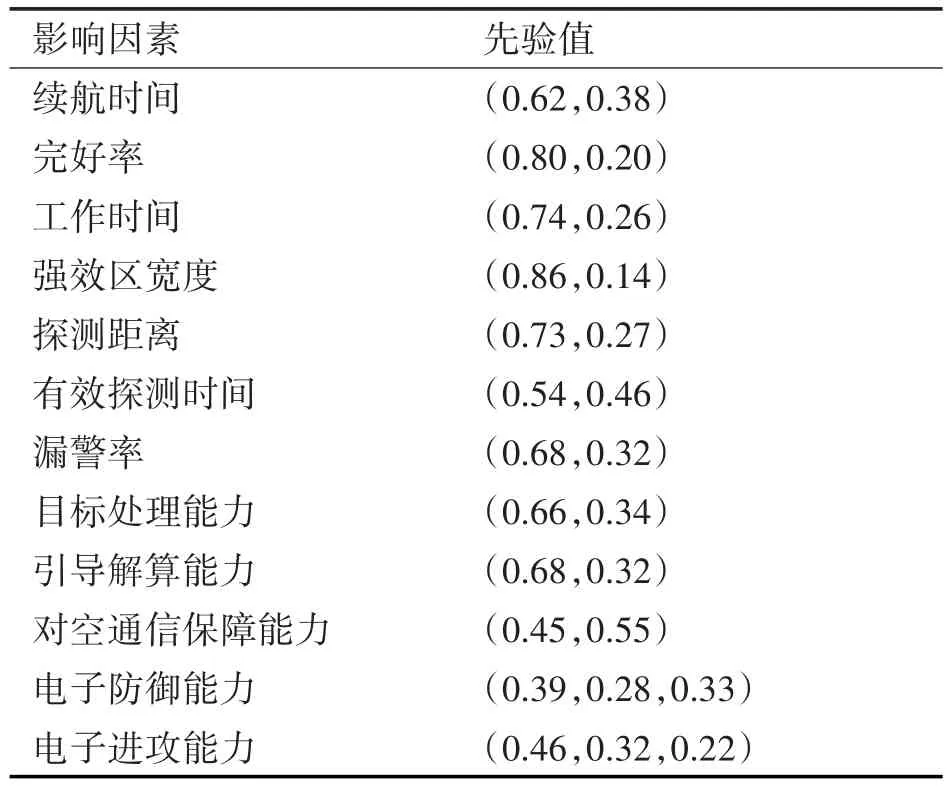
表6 相關先驗概率值

根據前節給出的條件概率矩陣，采用貝葉斯網絡推理機制，利用Netica構建并進行初始化的預警機持續作戰、對空探測、指揮引導以及電子對抗等方面的能力貝葉斯網絡分別如圖4所示。

通過圖4可以直觀地看出，該型預警機在執行反空襲作戰任務時，綜合作戰能力較強的概率為61.7%，說明具有一定的反空襲綜合作戰能力。然而通過仿真圖也能清晰地看出此型預警機作戰能力的短板：電子對抗和指揮引導能力方面稍顯不足。因此，指揮員需要根據任務轉化和作戰對象、戰場環境的特點，對預警機的作戰使用進行合理指揮與控制，以使預警機綜合作戰能力發揮到最高水平。同時，針對此預警機硬件指標較為薄弱的環節，如電子對抗能力，可以有針對性地提出升級改進的意見，以提高此型預警機遂行反空襲作戰的能力。

6 結語

本文在分析影響綜合作戰能力因素的基礎上，針對預警機反空襲作戰過程中不確定性因素多且難以定量分析的問題，依托貝葉斯網絡能夠充分利用領域知識和樣本數據來解決效能評估中信息量大、信息不完整問題的能力，建立預警機綜合作戰能力的貝葉斯網絡模型。通過算例仿真，驗證了模型的可行性。仿真結果直觀易懂，便于指揮員對預警機作戰使用的綜合把握，也為預警機的升級改造改造提供了參考依據。

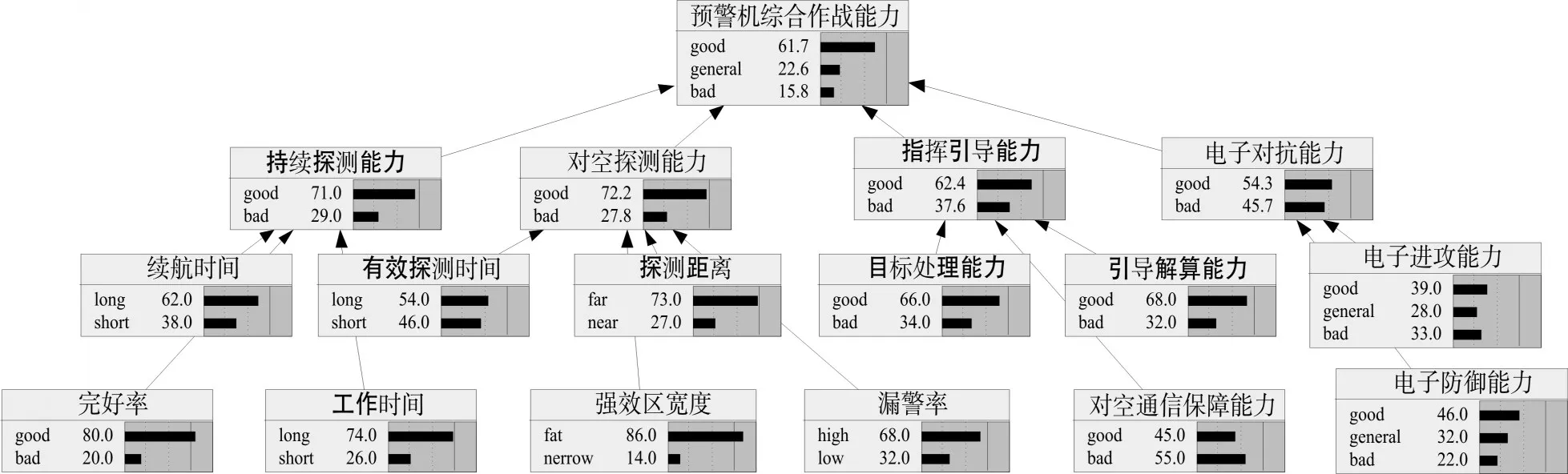
圖4 基于貝葉斯網絡預警機綜合作戰能力仿真圖