基于測試數據的裝備軟件質量評價

張 峰 孫隴平 陳 偉

（1.91404部隊 秦皇島 066000）（2.江蘇自動化研究所 連云港 222061）

1 引言

軟件質量是軟件符合明確敘述的功能和性能等需求、及文檔中明確描述的開發標準的程度。軟件測試是保證發布的軟件產品達到一定的質量標準的一種有效手段，測試數據是在軟件測試過程中產生的軟件缺陷數據，是評價軟件質量的重要方式。根據裝備軟件系統的特點，通過采集軟件測試過程產生的缺陷數據，建立軟件質量評價模型，開展基于測試數據的軟件質量評價技術研究，對于衡量以及促進提高軟件產品的質量有重要意義。

2 軟件質量評價體系

將軟件質量［1～2］從評價目標開始逐層分解到能夠獨立度量的層次，形成軟件質量要素、衡量標準和度量標準相結合的三層次結構。軟件的質量體系由一系列可以體現系統可見的行為化特征的高等級質量因素的質量要素組成，軟件質量是這些高等級質量要素構成的函數；每一個質量要素由若干衡量標準表示，而衡量標準是與軟件產品和設計相關的質量特征的屬性，如可靠性由精確性、容錯能力、一致性和簡單性來表示，正確性由可追蹤性、完備性和一致性來表示；每一衡量標準由若干定量化指標度量標準進行度量，而每個度量標準指標都是獲得質量準則的某些屬性的度量。軟件質量評價框架如圖1所示。

對軟件的質量要素、衡量標準進行充分分解，在此基礎上對衡量標準進行分解，形成多個可以度量的度量元。構建基于測試數據的軟件質量評價體系如圖2所示。

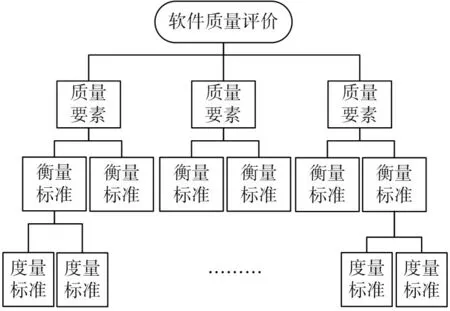
圖1 軟件質量評價框架

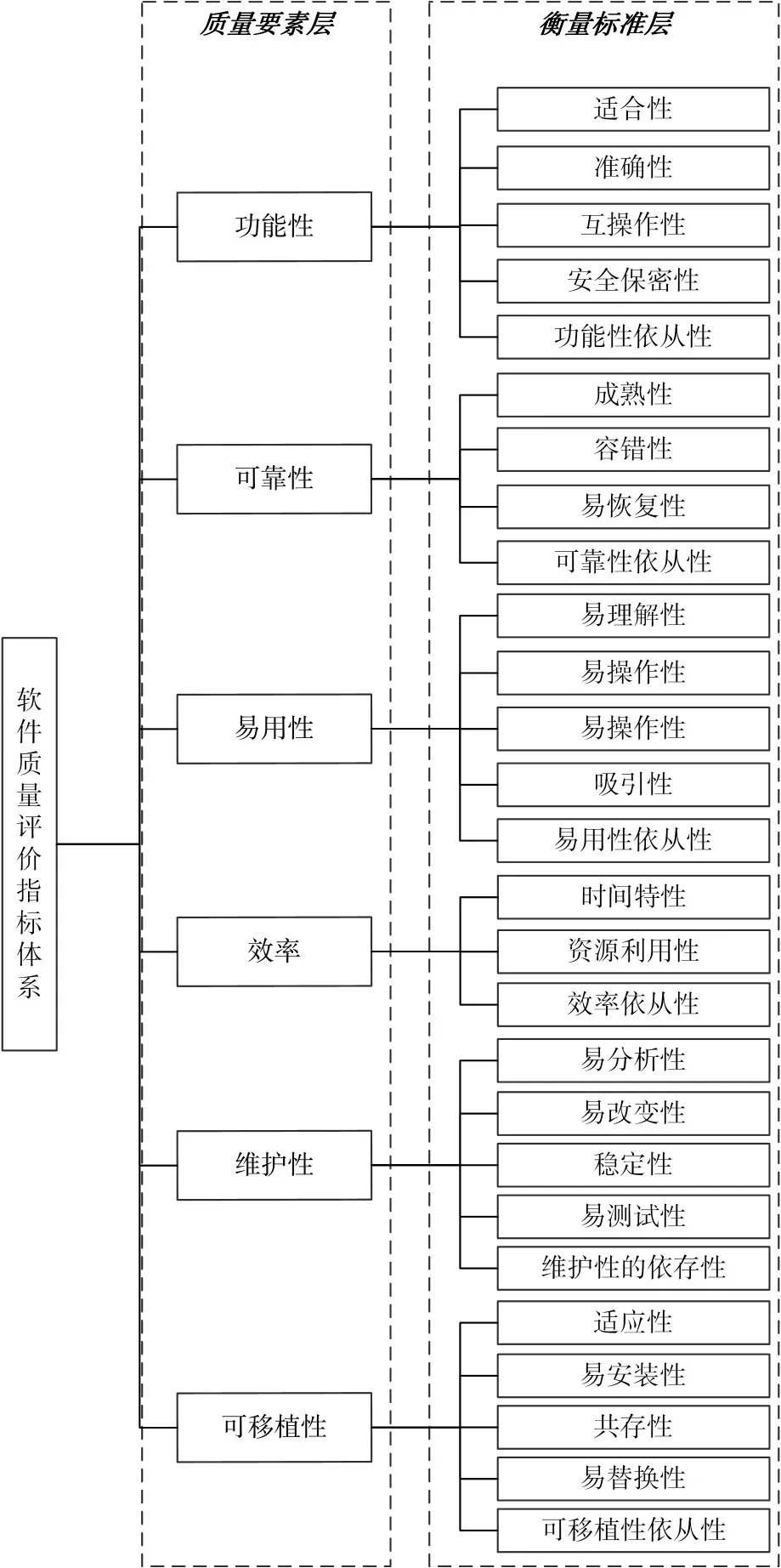
圖2 軟件系統質量評價指標體系

3 軟件質量評價體系映射

通過對測試數據進行相關度分析，建立屬性集；對測試數據按相關屬性進行縱向管理；建立度量標準庫和測試數據源倉庫的映射實體。通過研究測試流程到數據采集流程的映射，建立能滿足基于測試數據驅動的軟件質量評價的數據采集技術以及對測試數據進行分析和管理，從而建立以軟件質量評價為目的數據源倉庫。

軟件質量評價體系［3～8，10］與軟件測試數據映射最重要的是對分解的最末端的軟件度量指標的進行可計算度量的映射，形成軟件質量評價衡量指標可以使用軟件測試數據進行度量計算，而對應的軟件測試數據應該覆蓋軟件測試的全過程數據。軟件質量評價體系與軟件測試過程之間的對應關系如圖3所示。

圖3 軟件質量評價體系與軟件測試過程映射

3.1 軟件質量評體系映射方法

針對軟件質量評價體系的度量指標不能簡單地通過數據標定后定義為“好”、或“優”、“略”，這樣的指標數據找不到明確的邊界，既不能進行衡量標準、質量要素層級的匯總、計算，也無法體現出各個指標值之間的差距如何。通過模糊評價方法來評價軟件的度量指標。

1）模糊數學隸屬函數的定義

設在論域U上給定了一個映射

則稱A為U上的模糊集，A（u）成為A的隸屬函數（或稱為對A的隸屬度）。

上述定義說明，論域U的一個模糊子集A完全由其隸屬函數所刻劃，隸屬函數把U中每個元素u和區間［0，1］中的一個數A（u）結合起來，它表示u在A中的資格，即元素對模糊集合的隸屬程度。當A（u）的值越接近1時，則U隸屬于A的資格就越高。

2）定義計算公式

采用如下公式對軟件質量評價指標進行評價。

其中X為評價值，A為軟件過程中發現的軟件未滿足或滿足功能、性能、接口等數據，B為軟件需求功能、性能、接口等數據，其中0≤X≤1.0越接近1.0越好。

3.2 軟件質量評價體系映射關系

對照軟件需求描述的功能及、軟件測評大綱、軟件測試用例情況，通過對比軟件測試時發現的軟件缺陷，達到對軟件功能性度量，具體軟件功能性與軟件測試數據映射關系見表1。

表1 功能性與軟件測試數據映射關系

4 基于測試數據的軟件質量評價

4.1 評價模型概述

基于測試數據的軟件質量評價模型［9，11］的建立可分為如下步驟。

2）確定權重，由于基于測試數據的軟件質量評價指標體系具有不確定性，對于某些因素缺失的狀況，對缺失的權重進行二次分配；對于群組評價的情況下，給出群組評價的權重確定方法。

4.2 因素集及權重確定方法

1）因素集

軟件質量是各種特性的復雜集合［12］，會隨著應用的不同和用戶要求的不同而不同。針對基于測試數據的質量評價指標體系建立模型，對于具體軟件評判的特殊要求可在現有模型基礎上添加。

根據評價指標體系中的層次化結構，將軟件質量評判因素劃分為6個子集。

U1：功能性度量子集；U2：可靠性度量子集；U3：易用性度量子集；U4：效率度量子集；U5：可維護性度量子集；U6：可移植性度量子集。

每個子集中包含不同的子子集，子子集中的元素是質量特性中的子特性。U1={ }

U11，U12，...U15，其中U11：適合性；U12：準確性；U13：互操作性；U14：安全保密性；U15：功能依從性；其他子集中的元素依此類推。

其中，U11也是一個集合，其子集為適合性的度量標準。

U11={RM1，RM2，RM3，RM4} ，其中 RM1：功能的充分性；RM2：功能的完整性；RM3：功能實現的覆蓋率；RM4：功能規格說明的穩定性。其他子集中的元素依此類推。

2）標度

標度是用于事物之間進行比較的標準，包括比例標度和絕對標度。比例標度的測度往往需要進行比較才能確定，絕對標度的測度往往不需進行比較就可直接決定。

采用比例標度的方法對評價指標體系進行量化，采用矩陣法確定指標體系中個質量特性、子特性以及數據元素之間的權重。

比例標度一般把對事物的特性的比較分成5檔，用1～9的整數及其倒數對比進行測度（級差為2）。表2給出了一種對應關系。

表2 定性信息與定量值的對應關系

3）判斷矩陣

設Ce是遞階層次結構中第k層的一個元素，A1，A2，…，An是第k+1層且與Ce有聯系的元素，每對Ai和Aj的定量判斷可通過下面的模型進行計算，即相對于Ce，元素Ai和Aj哪一個重要，重要的程度如何。

稱 A=(aij)n×n為元素 A1，A2，…，An相對于 Ce的判斷矩陣，顯然判斷矩陣滿足：aij＞0，aij=1/aji，aii=1。因此對于一個n階判斷矩陣來說，需要輸入的信息量為n（n-1）/2（上三角或下三角部分）。相對于可靠性來說，可恢復性（A1）和容錯能力（A3）同等重要，成熟性（A2）稍重要于可恢復性和容錯能力，得到判斷矩陣：

4）殘缺判斷矩陣

由于知識的限制等原因，可能無法提供n（n-1）/2個判斷。如果判斷少于n（n-1）/2個，則稱判斷矩陣為不完全信息下的殘缺判斷矩陣。

5）從判斷矩陣產生權重

得到相對于某一特性的子特性或相對于某一子特性的指標符的判斷矩陣（包括殘缺判斷）后，可用特征根法求出一種質量特性（或屬性）的權重向量W。設判斷矩陣是A的最大特征根，特征根法就是求滿足AW=λmaxW的特征向量。需要說明的是，對于殘缺判斷矩陣，若元素aij殘缺，則用wiwj代替aij。問題是得到一組軟件質量特性的判斷矩陣A后，其最大特征根λmax是否存在？若λmax存在，相應的作為權重向量的特征向量W的分量是否全為正分量。

定理1 設A是n階判斷矩陣，則

1）A的最大特征根 λmax必存在，則 λmax≥n ；

2）A的最大特征根λmax有對應的正特征向量。

下面給出求判斷矩陣A=(aij)n×n的最大特征根λmax和相應特征向量W的迭代算法。

（1）設初值特征向量為W(0)，計算精度為ε＞0。為方便起見，一般取；

（2）計算W(k)=AWk-1，k≥1，其中Wk-1為上一次迭代得到的歸一化向量；

（4）以 W(k)作 為 權 重 向 量 W，并 求 出。

4.3 群組評價權重確定方法

通常人們習慣用引入群組評價的方法來保證評價的科學性，群組評價方法為：k個質量評價者根據判斷矩陣法對待評價的指標體系進行判定，分別給出各自的判斷矩陣。本節主要研究當出現K的相同（K的評價者的評價結果一致）或者不同（K的評價者的評價結果不盡相同）時，如何確定最終的判斷矩陣。

假定有k個軟件質量評價者，它們給出的一組質量特性判斷矩陣為

兩種處理方法包括如下兩種：

1）對k個判斷矩陣求均值，然后以均值矩陣為基礎，按照4.2節中介紹的方法求權重向量W。即：，對A求權重向量W。

分別對k個判斷矩陣按照4.2節中介紹的方法求權重向量Ws，然后對k的權重向量求均值。即：假定 As的權重向量為Ws( )s=1，2，...，k ， 則。

由于方法1）更接近于實際情況下的群組決策方法，采用1）進行群組評價的矩陣確定。

4.4 誤差解決策略研究

設相對于成熟性而言，子特性RM1，…，RM6的判斷矩陣為。若定性判斷 RM3稍重要于 RM2，RM2和 RM4同等重要，即 a32=3，a24=1，則一般就隱含著 RM3稍重要于RM4，即a34=a32·a24=3，但有時由于人的判斷的誤差，實際判斷時a34并不一定等于3，這種情況尤其在元素較多（判斷矩陣階數較大）時不可避免。為使判斷誤差在一個可接收的范圍內，引入一致性指標的概念。

定理2 若A為n階一致性判斷矩陣，則其最大特征根λmax=n。

定義2 設A為n階判斷矩陣，λmax是A的最大特征根，稱CI=(λmax-n)/(n-1)為A的一致性指標。

一致性指標反應了A偏離一致性的程度。不難看出，2階判斷矩陣總是一致的，階數n越大，即涉及的判斷因素越多時，一致性就越難達到。因此，用隨機一致性指標RI來修正一致性指標CI。隨機一致性指標可通過統計檢驗得到（表3）。

表3 一致性指標統計表

定義3 設CI和RI分別是判斷矩陣A的一致性指標和隨機一致性指標，稱CR=CI/RI為A的平均隨機一致性指標。

當CR＜0.1時，認為A具有滿意的一致性，即判斷誤差是可接受的。當然0.1這個界限值也可改變，它只是一個經驗值。

4.5 權值二次分配策略

由于測試數據是在測評過程中產生的一系列復雜數據。被測軟件各自特性的迥異會導致數據有可能能覆蓋到評價指標體系中的所有指標，也有可能只覆蓋到部分指標，為保證最終的加權值為1，應該對未被覆蓋到的指標進行二次分配。

當數據缺失時，根據質量評價的層次模型，依次判斷數據元素層的各個數據元素，若數據元素的缺失不會導致子特性的缺失，則將數據元素的權值按照該數據元素所在子特性下現有數據元素的權重比例，把缺失的數據元素的權值進行二次分配；若數據元素的缺失導致了子特性的缺失，則將缺失的子特性的值按照該子特性所在特性下現有子特性的權重比例，把缺失的子特性的權值進行二次分配。

假設集合U為質量要素，R為衡量標準，RM為質量標準。

?ui∈U，f()ui表示質量要素ui所占權重；

4.6 基于測試數據的軟件質量評價驗證

根據特征根法，求得可恢復性、成熟性和容錯性的權重值分別為 0.2，0.6和 0.2，λmax=3，CR=CI=0。

相對于成熟性而言，RM1稍重要于RM2，RM3明顯重要于 RM5，RM6稍重要于 RM4，RM4和RM2同等重要，RM3明顯重要于RM2，求出的權重值見表4。

λmax=6.005545，CI=0.001109，CR=CI/RI＜0.1。

表4 權重值表

指示符的測度值可通過與指示符有關的數據元素的絕對標度得到，并被映射成評價準備階段定義的等級。

為定義等級，使用兩個值0.4和0.6作為閥，并且使用3個等級值0，0.5，1分別表示差，中等和好（表5）。

表5 質量特性和子特性的等級值

質量特性的等級值可從與其相關的指示符的等級值和權重得到，成熟性的測度值為0.68。RM5的測度值NULL意味著指示符未被測度，所以上面的計算中就不包括RM5。

成熟性和可恢復性的測度值分別是0.68和0.7，通過映射，給這2個子特性等級值賦予1。容錯子特性未被度量。

可靠性的測度值為( )1×0.2+1×0.6/0.8=1，其等級值按等級定義應該是1。然而可靠性的等級值根據約束規則置為0.5。這個規則是：如果一個特性的等級值為1，它的子特性少于4個且其中至少有一個未被測度，則這個特性的等級值強制賦予0.5。

圖4僅展示了一個特性的測度，其他特性的測度可類似得到。當所有特性都被測度之后，就可根據質量需求確定軟件質量是否滿意。

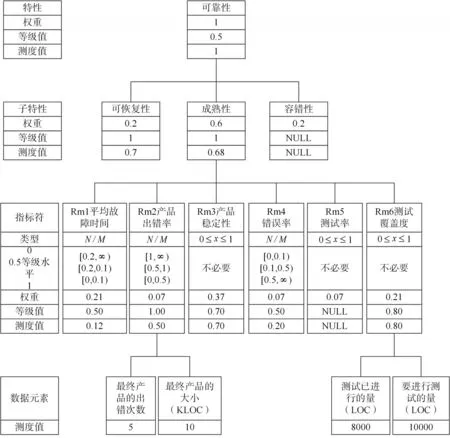
圖4 質量評價實例

5 結語

以軟件質量評價背景，針對軟件質量評價構建了軟件質量評價體系，并將軟件質量評價體系的質量要素、衡量標準分解細化，形成軟件質量度量標準；然后分析整個軟件測試過程，并將軟件測試過程產生的數據和軟件質量評價體系的度量標準進行映射，使測試數據覆蓋度量標準，為度量標準提供數據支撐；研究基于測試數據的軟件質量評價模型，針對建立的基于測試數據的軟件質量評價指標體系，研究因素集以及權重的確定方法，并對群組評價、誤差以及權值的二次分配給出了相應的策略。最后對軟件的可靠性研究成果進行實例驗證。提出的軟件質量評價體系和測試數據與軟件質量評價特性的映射，解決了軟件質量評價數據的來源，突破了測試數據采集的不客觀和不易采集性；研究成果可直接應用于軟件產品的質量評價分析，可以直觀、快捷地評價軟件質量，并能對多個軟件的質量指標進行細化對比，為軟件產品的質量評

價提供一種全新的、科學的、合理的方法，可以提高軟件質量評價的準確性。