基于Abaqus的不對中激勵力作用下軸系振動特性研究

樓京俊 王建午 劉麗濱 楊慶超

（1.海軍工程大學船舶與海洋學院 武漢 430033）（2.海軍裝備部駐上海地區第二軍事代表室 上海 200120）

1 引言

軸系對中不良時，在彈性聯軸器和軸系各連接法蘭處會產生強烈的不對中激勵，這將改變軸系原有的振動傳遞和響應特性，從而導致軸系異常振動［1～4］。目前，關于軸系校中不良與軸系振動特性之間相互影響規律的研究較多，付波、王延溥、徐俊輝等從軸系不對中時的振動特性、振動診斷與處理方法等角度對軸系不對中與軸系振動之間的相互關系進行了研究［5～7］；李方、周奇鄭等推導了不對中狀態下的軸系振動響應計算公式，并分析了不對中量對其振動響應曲線的影響［8～9］；楊俊等分析了三種不對中情況下彈性聯軸器的受力狀態，通過對不對中激勵力進行數值仿真和臺架試驗研究了軸系不對中量對軸系振動的影響［10］；蔣義海、吳振宇等以轉子不對中故障平臺為例，基于計算機軟件建立了軸系仿真模型，計算并分析了不對中故障下軸系的振動響應特性［11～12］。

為進一步弄清軸系不對中激勵力作用下的軸系振動特性，掌握軸系校中對其振動特性的影響，本文將對激勵力作用下的軸系有限轉子動力學方程進行推導，同時根據實船軸系在Abaqus軟件中建立其有限元仿真模型，并對模型開展模態分析與瞬態動力學分析，由此得出不對中激勵與軸系振動特性之間的相互影響關系。

2 軸系有限轉子動力學方程

軸系實質上是一個質量連續分布的轉子系統，用有限元法可將其離散化為許多具有若干集總質量的多自由度轉子單元，這些轉子單元按位置與受力狀態可進一步分為兩大類：梁單元與軸承支承處的的轉子單元。

1）梁單元動力學方程

梁單元模型如圖1所示，每一個梁單元都由兩個節點組成，每一節點有沿水平方向位移x、沿豎直方向位移y、繞水平軸旋轉角度θx與繞豎直軸旋轉角度θy四個空間自由度。該梁單元的空間位移向量可表示為

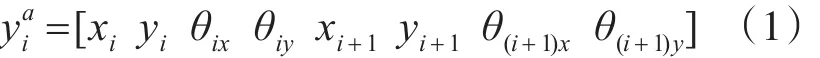
式中，i、i+1為節點編號。

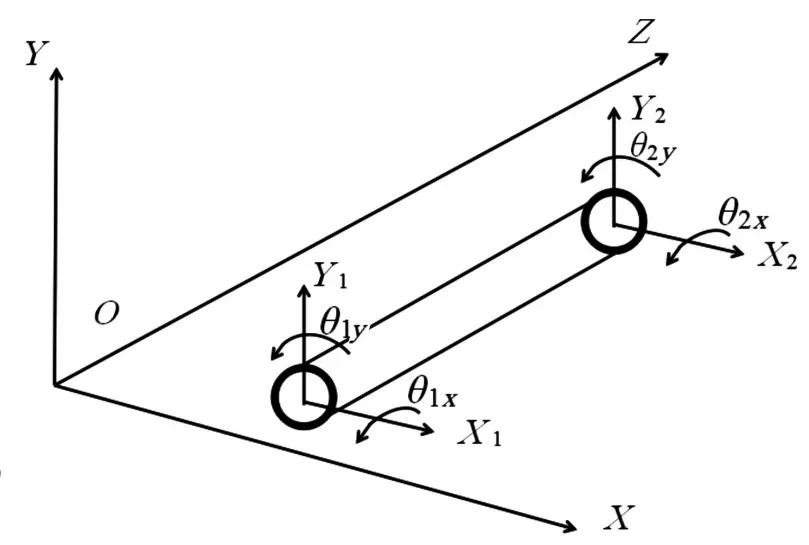
圖1 軸系梁單元模型圖

由拉格朗日法可推導出該梁單元動力學方程：

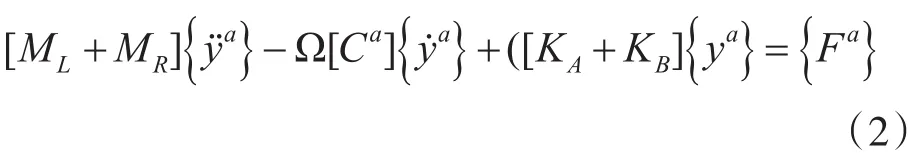
式中，ML、MR分別為梁單元位移質量矩陣與轉角質量矩陣，Ca為梁單元阻尼矩陣，KA、KB分別為梁單元彎曲剛度與軸向剛度矩陣，Fa為梁單元上作用的不平衡力、外載荷等。

2）軸承支承處轉子動力學方程

與梁單元動力學方程類似，線性軸承支承處轉子單元動力學方程為

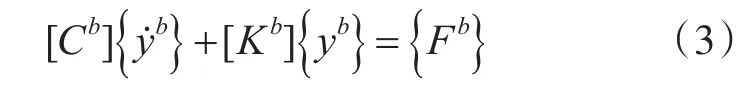
式中，yb、Cb、Kb、Fb分別為各軸承支承處轉子單元的位移向量、阻尼矩陣、剛度矩陣及外載荷。

綜合各軸系轉子單元并將它們的質量、剛度、阻尼、受力進行等效合并，可得到整個軸系動力學方程：

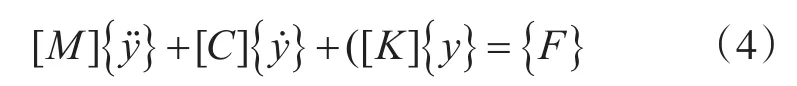
上式中，F含軸系各零部件重力、外載荷、軸系不平衡力及不對中造成的激勵力。

3 軸系有限元模型的建立

某船舶推進軸系結構簡圖如圖2，該軸系由艉至艏依次為螺旋槳、艉軸、艉后軸承、艉中軸承、艉前軸承、推力軸、推力軸承、彈性聯軸器、經航電機、中間軸、中間軸承、輪胎離合器。

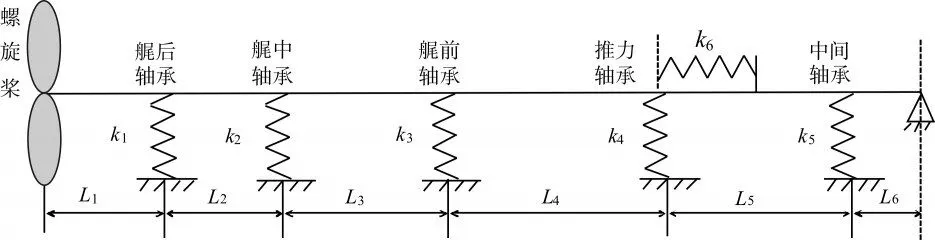
圖2 某船舶推進軸系結構簡圖

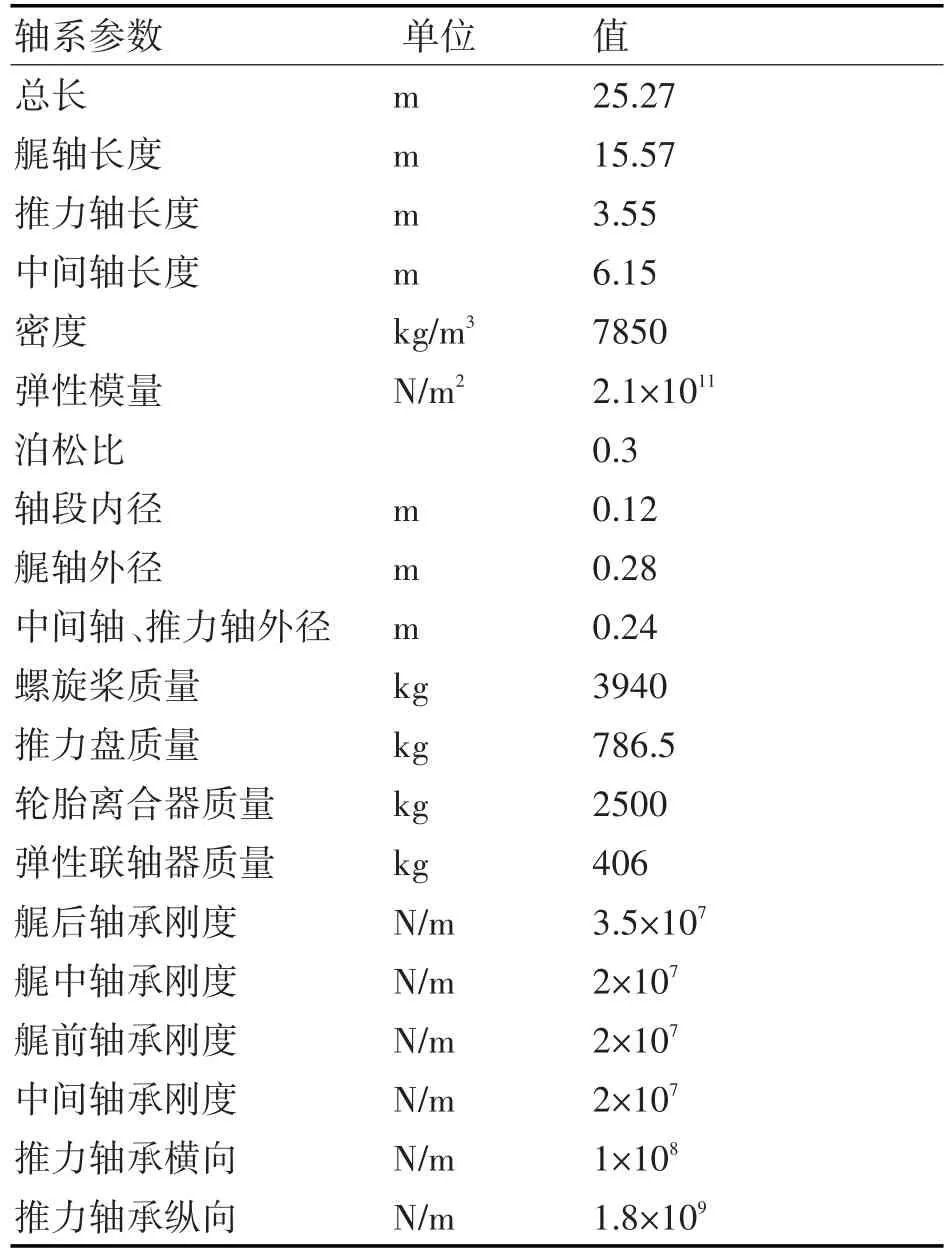
表1 軸系基本參數表

對上述推進軸系進行合理簡化并在Abaqus中建立其仿真模型，用到的軸系基本參數如表1；建模時采用三維可變形梁來模擬軸系，用Springs單元來模擬各支承軸承，螺旋槳用實體七葉槳進行模擬，軸系各零部件用點質量進行模擬并施加于對應位置；由于軸系艏端以輪胎離合器與主推進裝置相連，在建模時將其作簡支處理；在各質量集中單元處對軸系進行分段處理，并在分割節點處設置點質量/慣性值用以賦予各部件質量屬性；另外，在各軸承支承處創建參考點，用于模擬軸承基座并固定軸系。

在幾何模型中首先根據軸系基本參數表設置其材料、截面屬性及各零部件點質量，然后設置各軸承線性彈簧/阻尼連接器剛度。在連接器剛度設置時應注意計入各軸承工作長度對支撐彈簧數量的影響，此處用3個等間隔垂向和水平彈簧模擬艉后軸承，用2個等間隔垂向和水平彈簧模擬艉中、艉前軸承，用1個垂向和水平彈簧模擬中間軸承；推力軸承在設置時不但要計入水平、豎直方向的剛度，還需計入縱向剛度的影響，故用1個水平、1個垂向和1個縱向彈簧進行模擬。此外，由于艉后軸承離螺旋槳較近，受螺旋槳“懸臂作用”影響明顯，一般具有較大軸承負載，因此在賦值時常將其垂向油膜剛度設置得比水平方向油膜剛度稍大，而使其他各軸承垂向剛度與水平剛度保持一致。各軸承剛度設定值見同表1。

根據實際情況，在各軸承支座模擬結點上施加固支邊界條件，同時在螺旋槳中心處設置一參考點，并將該參考點與軸系相應結點建立coupling約束。最后對設定好的軸系幾何模型進行網格劃分與單元類型設置，得到其有限元模型如圖3，其中軸段上共生成了223個結點和212個單元。

圖3 軸系有限元模型示意圖

4 不對中激勵作用下軸系振動特性分析

4.1 軸系模態分析

各激振力在傳遞過程中首先要經過軸系，軸系的固有特性會對各激振力產生不同程度的放大或減弱效果，因而對軸系開展模態分析以弄清軸系本身固有特性是研究不同激勵力作用下軸系振動特性的前提。

在模型中建立頻率分析步，采用Lanczos法對軸系模態振型和頻率進行求解。計算得到軸系一、二、三階縱振振型如圖4所示，其對應模態頻率分別為 40.30Hz、90.34Hz、180.05Hz，由圖可知，軸系一階縱振振型最大變形處主要集中在艉軸中部，二階縱振主要集中在在中間軸附近，三階縱振主要集中在艉軸艏端。

圖4 軸系縱振振型圖

軸系前4階橫振振型如圖5所示，對應模態頻率分別為 8.69Hz、12.51Hz、18.29Hz、20Hz，一階橫振變形主要發生在艉軸靠近螺旋槳一端，二階橫振主要發生在在中間軸承附近，三、四階橫振主要發生在艉軸和中間軸上，各橫振節點基本位于軸承支承處。

4.2 不對中激勵作用下軸系振動響應分析

從模態分析得到的各階振型圖可以看出，不同頻率激勵力作用下，軸系各連接法蘭和彈性聯軸器處均會發生較大變形，這將改變軸系的校中狀態和工作性能。軸系聯軸器不對中是指其兩端轉子中心存在一定的位移或角度偏差，主要分為三種型式：平行不對中、角度不對中和綜合不對中，不對中聯軸器對軸系振動產生的激勵作用主要體現在其兩側節點會產生額外不對中激勵力矩，該激勵力矩最終以反作用力的形式作用在軸系上并引發軸系振動；這種不對中激勵復雜且難以定量計算，它會隨著軸系運轉工況、聯軸器在軸系中的位置以及不對中量的不同而發生改變。

圖5 軸系橫振振型圖

由文獻8中相關理論可知，軸系不對中產生的激勵力為周期力，其主要諧波分量為軸系工作頻率的1倍頻與2倍頻。在Abaqus中進行仿真時，需要先根據模態分析得到各軸系固有頻率fi并按公式：ni=60fi求解出軸系臨界轉速ni，以避免設定的工作轉速與臨界轉速相重合而引起共振；因此，在模型中把軸系工作轉速設定為15r/s，同時將軸系不對中激勵力分解為x、y兩個方向上的諧波分量有：Fy=A1coswt+A2cos2wt和 Fx=A1sinwt+A2sin2wt。按照上述諧波分量表達式將單位不對中激勵施加在聯軸器相應節點位置，并對軸系進行瞬態動力學分析，以艉軸中間點為響應考察點，計算得到軸系振動響應曲線如圖6，其中，圖6（a）、6（c）、6（e）為考察點三個方向振動響應時域圖，對它們分別進行傅里葉變換得到考察點振動響應頻譜圖如圖6（b）、6（d）、6（f）。

由圖6（a）、6（c）、6（e）可知，不對中激勵力作用下軸系豎直、水平方向上的振動響應幅值比縱向振動大了約兩個數量級，這表明聯軸器不對中激勵在軸系上的傳遞途徑主要沿各軸承水平方向與豎直方向，只有小部分以縱向傳遞的方式由各軸承基座傳遞給船體；從圖6（b）可以看出，不對中激勵力作用下軸系縱向振動響應峰值主要出現在26Hz、30Hz、32Hz、40Hz、42Hz、103Hz、131Hz及180Hz等處，結合模態分析結果可以發現：26Hz、32Hz、42Hz、131Hz為軸系橫振固有頻率，40Hz、180Hz為軸系縱振固有頻率，103Hz為螺旋槳模態頻率，又因為軸系轉頻為15r/s，縱振響應曲線在30Hz出現了最高峰值，這表明軸系不對中激勵在沿縱向傳遞時，傳遞形式主要為其2倍轉頻分量；與圖6（b）分析過程類似，發現在圖6（d）、6（f）中，不對中激勵力作用下軸系豎直、水平方向的振動響應峰值除了出現在各結構固有頻率處，在15Hz、30Hz也分別出現了較強烈的響應峰值，其中30Hz處還出現了最高峰值，由此可見，軸系不對中激勵在沿豎直、水平方向傳遞時，傳遞形式為其1倍轉頻分量與2倍轉頻分量且以2倍轉頻為主要頻譜。綜上所述，不對中激勵下軸系頻率響應峰值主要在1倍轉頻與2倍轉頻處，分別為15Hz、30Hz，仿真結果與理論值基本一致。

5 結語

利用有限單元法將軸系離散成了多個具有集總質量的轉子單元，同時推導出了各轉子單元及整個系統的動力學方程；在此基礎上以某實船軸系為例，在Abaqus中搭建了軸系有限元仿真模型，通過對模型開展模態和瞬態動力學分析，得到了軸系各階模態振型、固有頻率及不對中激勵力作用下的軸系振動響應曲線，通過對比研究發現不對中激勵作用下軸系的振動響應頻譜主要表現為1倍轉頻與2倍轉頻的特征，其中2倍轉頻為主要分量且能通過縱振、橫振相結合的方式進行傳遞，1倍轉頻則主要通過軸系橫振的方式進行傳遞，這與理論分析基本相符，驗證了該仿真模型的正確有效性。

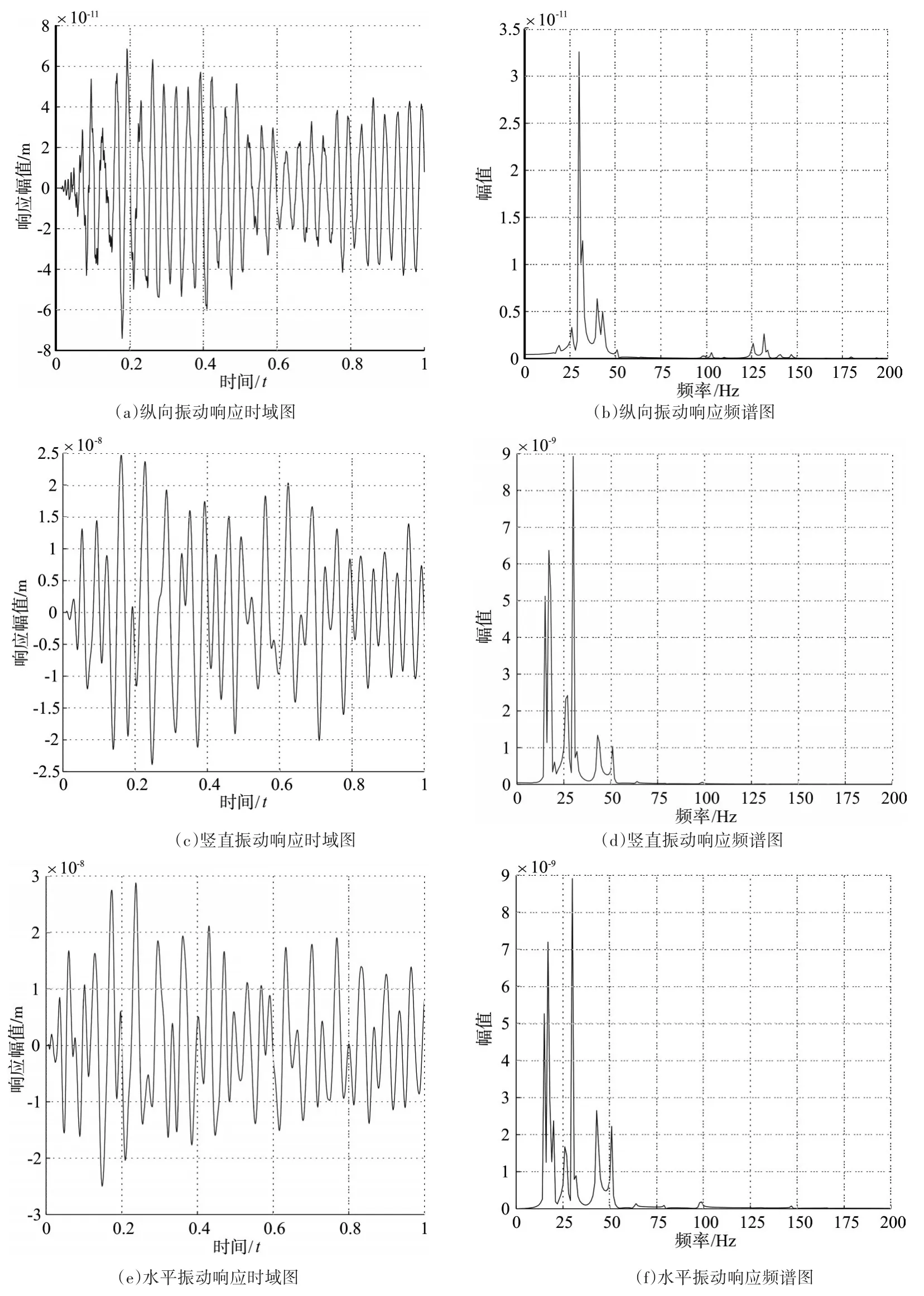
圖6 不對中激勵力作用下軸系振動響應