多元函數取值范圍問題的常見求解失誤

廣東省深圳市鹽田高級中學 (518083)

羅 誠

在解答多元函數取值范圍問題時，由于涉及多個變元，在解題過程中，相對于單變量函數取值范圍問題，更容易出現這樣或者那樣的失誤.有感于此，本文擬將解決這類問題時的常見失誤進行梳理歸類，以供教學參考.

一、疏漏顯性題設

對于多元函數取值范圍問題，關聯多個變量，常常題設較多.在求解過程中，容易出現顧此失彼的情況，以至于疏漏顯性題設導致解題失誤.

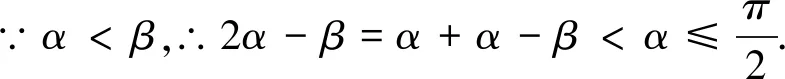
圖1

+∞).

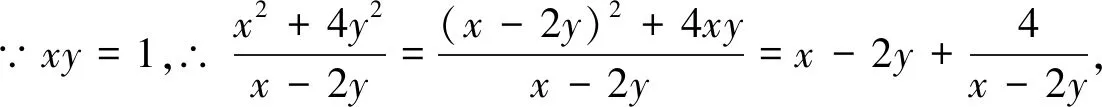
圖2

二、忽視等號成立

等號能否成立，關乎到多元函數取值范圍的上下確界.在解題過程中，倘若不慎，就有可能出現等號不成立的情況，從而由此出現解題失誤.

例3 若正數x,y滿足x+3y=5xy，求3x+4y的取值范圍.

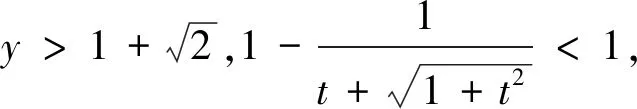
三、變更變元范圍

求解多元函數取值范圍問題，在變形的過程中，出現不等價變形，引起變更變元范圍的失誤是司空見慣的.

例5 已知實數x,y滿足3x2+2y2=6x,求u=x2+3y2的取值范圍.

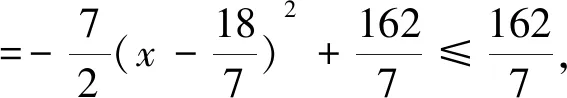
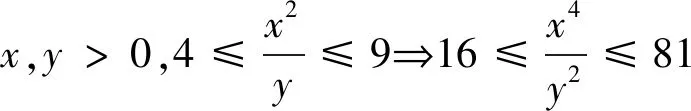
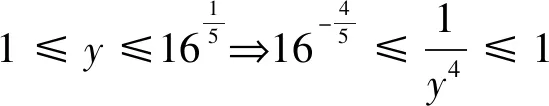
剖析:上述解法，變形過程擴大了變元x,y的取值范圍，正確解法如下：

四、描繪圖像失真

限于直觀的局限，難免在描繪圖像時，使描繪出的圖像產生失真，并由此形成解題失誤.

例7 在平面直角坐標系中，點A，B，C的坐標分別為(0，1)，(4，2)，(2，6)．如果P(x，y)是△ABC圍成的區域(含邊界)上的點，那么當u=xy取到最大值時，點P的坐標是．

圖3

誤解:畫出圖形，如圖3，聯想到線性規劃問題解法，由圖形直觀可知，當點P與點C(2,6)重合時，w=xy的最大值為12.

辨析:上述解法似乎無誤，但這種解法是由于描繪圖像失真的誤解.

請看以下的定量分析：

由題意可得線段BC的方程為y=-2x+10(2≤x≤4)，代入u=xy可得u=x(-2x+10)=

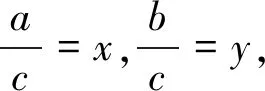
圖4

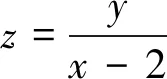
辨析:上面給出的是一種典型的圖像失真導致的誤解.

圖5