PCA 中兩種數據缺失處理方法的比較

左航

（國網鄭州供電公司，河南 鄭州 450000）

第一種方法稱為基于均勻性分析的數據缺失被動(MDP)方法。第二種方法是加權低秩近似法(WLRA)。2 種方法對人為生成的不完全數據進行分析，并用平均同余系數對原始完整數據進行參數恢復能力檢驗。

1 2 種方法的介紹

B 為n ×t 矩陣，C 為m ×t 矩陣，D 為按降序排列的奇異值的t ×t 對角矩陣。設Br,Cr和Dr表示B、C 和D 對應于r 廣義奇異值的部分。

并且

獲得上述解決方案至少有2 個不同的標準：一個是

uj是權的r 元素向量,和表示任意矩陣Y。

另一個是

1.1 缺失數據被動(MDP)

通過文獻概括(4)推導出MDP 方法：

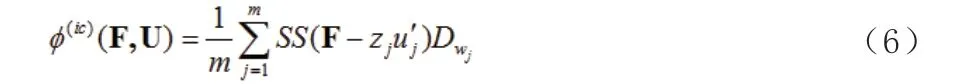
其中：

簡化最小化過程。上述最小化問題為

F 服從于(7)。改為

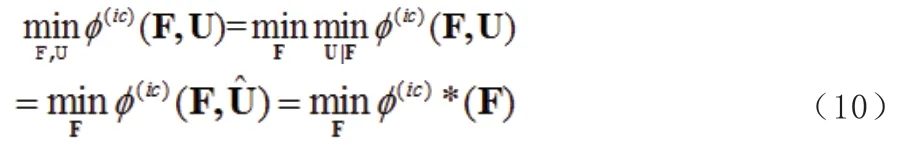
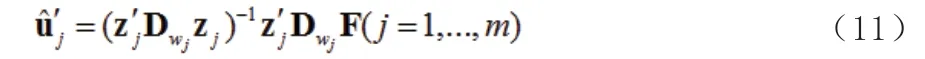
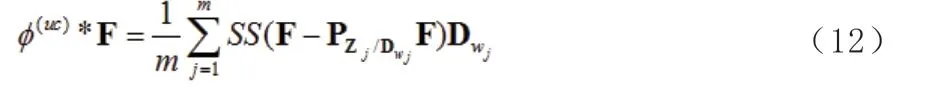
其中：

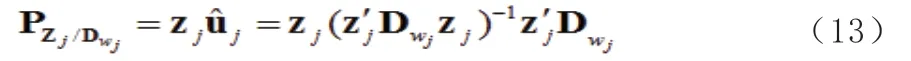
(12)寫成：

其中

(14)相對于(7)，F 的最小化等價于

(16)通過廣義本征方程得到

1.2 加權低階逼近(WLRA)

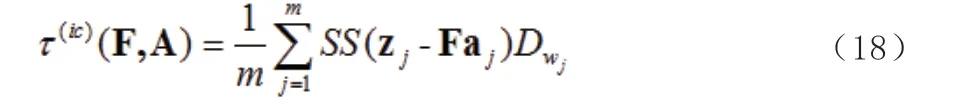
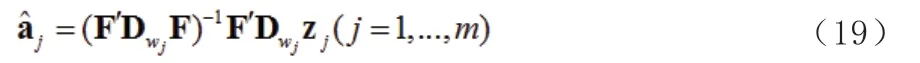
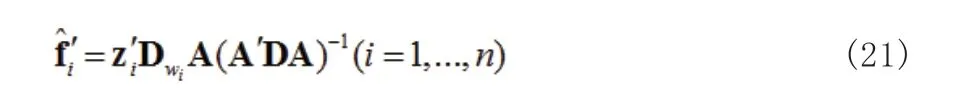
2 實證研究

MCAR 條件下的食物和癌癥數據：數據集是文獻[10]編譯的一個小數據集。規定的比例（10、20 和30）隨機(MCAR)初始完整數據。首先將PCA 應用于原始完整數據，發現第一個我們的組分占總變異的70.8、14.1、6.2 和5.3。

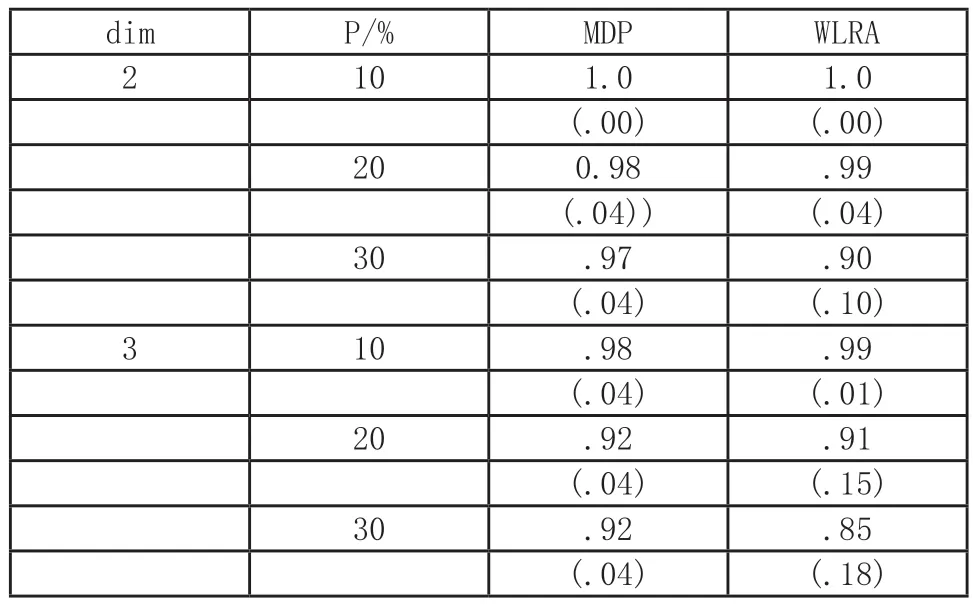
表1 食品和癌癥數據組分負荷恢復：同余系數的均值和標準差（括號內）

有2 個具有經驗意義的組成部分，一個是強的，另一個是相對弱的。決定檢查1 ～3 的組分數量。表1 總結了主要結果。表中的第一列表示提取組分的維度。第二列表示刪失率。接下來的兩列顯示了2 種方法獲得的組分負荷一致性系數的平均值和標準差。少量組件和低刪失率的回收率極佳。隨著維數和刪失率的增加，恢復率下降。然而2 種方法的恢復惡化率并不一致。

3 結語

本文考察了它們的參數恢復能力，作為缺失數據比例、解的維數和刪失中非隨機性程度的函數。在MCAR 情況下，當數據的維數和缺失比例較小時，所有方法都能很好地工作。隨著這些因素的增加，它們的性能下降，但使用 WLRA 方法時，惡化速度往往更快。可以提供的一個一般性建議是，都應保持組件數量盡可能減少。高維解往往會增加提取弱分量的機會，這總是不利于參數恢復。