運用多元表征教學策略促進大班幼兒模式能力發展的行動研究

張迎春 李娟 沈童 鄭紅玲 王麗紅 李瑩

[摘 要] 模式能力是幼兒形成邏輯思維的重要前提，對幼兒以后的數學學習和發展有著深遠影響。為了提高幼兒的模式能力，本研究采用行動研究范式，運用多元表征的教學策略對實驗班和對照班幼兒各30名進行為期4個月的干預，結果發現在行動研究結束后，實驗班幼兒的模式能力在量和質兩個方面都獲得了提升。就量的方面來說，實驗班幼兒的模式能力在前后測及與對照班的對比中都有明顯提升。就質的方面來說，實驗班幼兒更加勝任模式的創造和轉換任務，能夠把模式概念運用于日常生活中，并且樂于開展模式活動。參與行動研究的教師對多元表征教學策略不再“抵觸”，運用多元表征教學策略的能力得到了提高。合理的干預方案和研究小組成員的協作是行動研究富有成效的關鍵因素。教師在數學教學中應善于幫助幼兒理解數學關系，鼓勵幼兒選擇多種方式進行表征，并在日常生活中注重對幼兒多元表征意識的培養。

[關鍵詞] 模式能力;多元表征;行動研究

一、問題提出

模式“反映的是客觀事物和現象之間本質、穩定、反復出現的關系”。[1]模式作為“任何可復制的規律”，具有重復性和可預測性。[2]兒童對模式關系的理解和認識，不僅有助于兒童通過模式的概括去發現、理解數學自身獨特的結構以及數、幾何、測量等各大主題之間的聯系，使兒童獲得有效的數學圖式，而且能夠為其以后抽象的數學知識（如函數、代數觀念）的學習奠定基礎，促進兒童對數學與其他學科之間聯系的理解和掌握。[3]

而模式表征是模式這一概念的重要組成部分，關于數學表征，不同的學者有不同的解讀。有學者認為數學表征是指“運用其他的形式表達數學概念或關系的過程”。[4]也有學者補充“數學表征不僅僅是指兒童用某種形式，如數學符號、圖表及口頭表達等，表達要學習的或處理的數學概念或關系，還包括兒童在解題過程中轉換表征方式的能力”。[5]而多元表征這種“提供多樣化的、彈性的信息呈現方式，讓學習者分別使用文本、圖片、聲音、動畫、多媒體等來顯示同一知識點或學習對象的形式，能最小化學習障礙，最大化學習機會”。[6]因為在數學教育中，多元表征方式可以幫助學生更加深入地理解數學的概念以及概念之間的關系，提高學生問題解決能力，增加數學學習的趣味性。

但是，我國的學前數學教育中，沒有給予模式及其多元表征應有的重視。在實踐中，模式尚未作為一個獨立的概念被提出來，而是和數學領域中序列、樣式混在一起。[7]且在當前的幼兒園模式教學中，存在著操作材料單一、模式教學較多停留在視覺層面等問題，這些問題限制了兒童對模式本質的理解和認識。[8]那么，針對當下模式教學的不足，我們應該如何促進幼兒模式能力的發展呢？黃瑾（2015）指出，教師應該“鼓勵幼兒從視覺、聽覺、動覺上去感受相同的模式規律性，幫助幼兒嘗試將模式的一種表征形式轉化為另外一種表征形式”。[9]杜青霞（2014）按照表征的形式（感覺通道）也提出，數學表征主要包括聽覺表征、視覺表征和動作表征，且三者一般都是相互伴隨出現。[10]

然而，在教育實踐中，到底該如何設計具體的教育活動，如何幫助一線教師掌握利用多元表征模式來促進兒童模式概念的獲得，進而把這種多元表征模式遷移到其他教育活動中呢？傳統上，給教師單純講授知識的方式效果并不太好，[11]讓教師在實踐中開展行動研究是大家公認的促進其專業發展的有效形式，[12]因為行動研究中獲得的知識能夠讓教師們靈活地處理復雜的、多樣的課堂情況，并使知識得到遷移。[13]本研究正是采用協同式行動研究范式，由幼兒園一線教師、H大學學前教育專業碩士生導師、學前教育專業的研究生組成研究共同體，以促進兒童模式能力發展為出發點，對幼兒進行為期四個月的多元表征（聽覺、視覺和動作）教學干預，以此來探析多元表征教學模式及其效果。

二、研究方法

本研究采用行動研究范式。行動研究，是指由社會情境（教育情境）的參與者（教師、校長、學校輔導員或其他教學相關人員）為提高對所從事的社會或教育實踐的理性認識，為加深對實踐活動及其依賴的背景的理解所進行的反思研究。[14]本研究是基于實踐中模式教學的不足而對多元表征教學有效性進行探析的研究，而行動研究則是一種“與教育具體實踐密切相關，由一線工作者與教育學者共同參與，以行動進行研究，以研究促進行動的實踐性研究方法”。[15]因此，本研究與行動研究的思路相切合，故選擇此研究范式。

（一）研究對象

本研究的研究對象來自于河北省保定市Q園， Q園是一所省級示范幼兒園，但是在幼兒數學方面的實踐研究經驗并不豐富。已有研究表明，大班幼兒基本上開始具備模式轉換的能力，也就是多元表征的能力，而小班和中班幼兒一般還不具備。因此，本研究選擇大班幼兒作為行動研究實施的對象。Q園一共有6個大班，其在實施幼兒數學教育時參考來源有兩個：一個是Q園自主研發的園本教材，另一個是Q園購買的幼兒數學教育教材。

本研究從Q園6個大班中隨機抽取2個班共60名幼兒作為研究對象，一個班為實驗班（30人），一個班為對照班（30人），具體情況見表1。

（二）行動研究干預方案

1. 行動研究小組成員介紹。

行動研究既可以是個人的，也可以是多人協同合作的。本研究采用的是多人合作模式，由學前教育專業研究生、實驗班級教師、H大學學前教育專業碩士生導師共同構成行動小組。各成員的基本情況與分工如下頁表2所示：

2. 行動期間，實驗班與對照班模式教學的基本情況。

在行動研究期間，實驗班模式領域的教學沒有實施Q幼兒園園本教材和專門數學教材中的相關內容，而是由行動研究小組按照多元表征的原則設計實施模式領域的教學;對照班模式領域的教學由其本班教師實施，教學內容來自Q園的園本教材和專門的幼兒數學教材。Q園有基本的教學進度要求，因此，兩個班實施的模式方面教育活動數量基本一致，不同的只是教育形式，即實驗班更加注意多元表征下的模式教育，對照班對此并無特意關注。

在行動研究期間，Q園同意由研究者A執教并提供測查場地的行動小組定期交流的會議場所，為整個行動研究的順利實施提供了便利。

3. 干預方案的具體介紹。

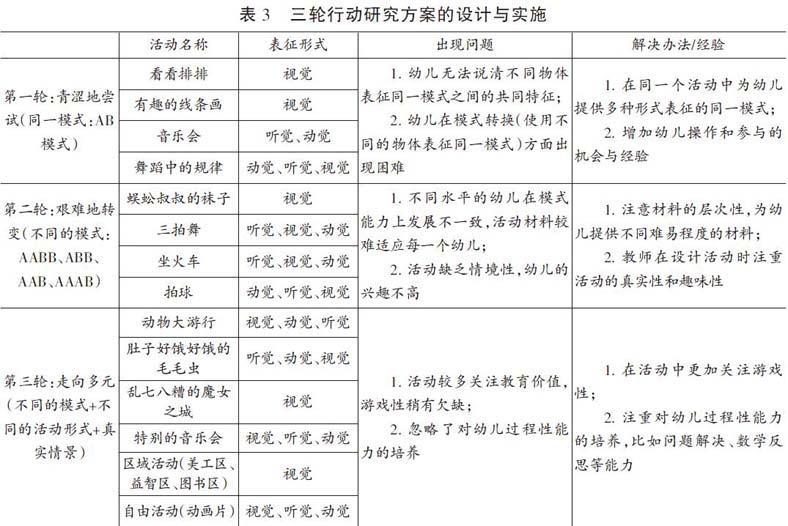
行動研究是一種“動態生成性研究”，其在不斷變化的教育實踐中實施，因此，研究者需要根據實踐中遇到的問題邊研究邊修改方案。[16]在本研究中，除了第一輪行動方案根據大班幼兒模式能力的前測結果制定，第二、三輪的研究方案則是結合前一輪行動研究過程中遇到的問題而制訂。詳見下頁表3。

在模式類型方面，主要分為重復性模式和發展性模式。周蔥蔥、林泳海提出幼兒式樣（模式）的發展經歷了“從循環式樣發展到重復式樣，再發展到滋長式樣（遞增模式或發展性模式），最后發展到變異式樣”。[17]因此，在前兩輪的行動研究中主要涉及重復性模式，在第三輪的行動研究中涉及發展性模式。

在模式結構方面，涉及多種結構的模式。[18]在第一輪的行動研究中，主要涉及AB結構的模式，到后期進行反思的時候，研究者與行動小組一致認為：單一的模式結構會使幼兒在強化的過程中記住某一模式，而不是真正地掌握模式的本質，因此，在后兩輪的行動研究中，會涉及多元的模式結構。

在表征形式方面，本研究在杜青霞（2014）的分類基礎上，將表征形式定義為視覺、聽覺、動覺上的表征，并據此進行模式活動設計，但每節活動涉及的表征形式并不固定，由活動內容本身決定。

在活動形式方面，既包括集體活動也包括區域活動和自由活動。對大班兒童模式能力的前測表明，大班幼兒在模式轉換方面的分數普遍較低，即普遍不擅長模式的多元表征。所以行動之初，行動小組想用集體教授的方式，讓幼兒感知多元表征的形式。但是隨著行動研究的深入，我們越來越認識到在區域活動和自由活動時，存在大量模式多元表征的機會，所以在第三輪行動研究時，加入了這兩種活動形式的干預。

具體的活動方案如表3所示：

（三）測查工具

在參考史亞娟（2003）[19]、楊錚錚（2007）[20]、高燕（2009）[21]、陸敏[22]等人的研究成果及《3～6歲兒童學習與發展指南》模式部分的測查題目的基礎上，本研究結合大班幼兒年齡特點自行編制了測查工具，根據預測查的結果對測查工具進一步修改;隨后結合學前數學教育領域兩名專家的意見，最終形成了正式測查工具。且本研究是測查幼兒的外顯行為，評分標準也簡單易操作（幼兒正確完成任務計1分，錯誤計0分），因此測查工具信度較有保證。

測查題目主要從表征形式（視覺、聽覺、動覺）、模式類型（重復性模式和發展性模式）、模式能力（模式復制、模式填充與擴展、模式創造、模式轉換）三個維度進行設計，共21道題。具體包括：

1. 聽覺的模式：包括重復性模式（ABC）和發展性模式（ABABBABBB）。①ABC 結構的模式：主試展示三種不同樂器并按規律敲出聲音，重復一次以后，請幼兒敲出聽到的規律，并詢問幼兒“接下來是什么”，最后請幼兒用不同的方式表示這個聲音的規律;②ABABBABBB結構的模式：主試播放“貓—狗—貓—狗—狗—貓—狗—狗—狗”的叫聲，重復一次以后，請幼兒模仿聽到的聲音，并詢問幼兒“接下來應該怎么叫”，然后請幼兒用不同的方式表示這個聲音的規律;幼兒聽完兩個有規律的聲音之后，主試請幼兒使用一種、兩種或三種樂器創造與教師不一樣的聲音模式。

2. 動作的模式：包括重復性模式（ABC）和發展性模式（ABABBABBB）。①ABC 結構的模式：主試做出“拍肩—拍手—拍腿—拍肩—拍手—拍腿—拍肩—拍手—拍腿”的動作，重復一次以后，請幼兒重復主試的動作（三組以上），并詢問幼兒“接下來是什么”，最后請幼兒用不同的方式表示這個動作的規律;②ABABBABBB結構的模式：主試做出“拍肩—蹦—拍肩—蹦—蹦—拍肩—蹦—蹦—蹦”的動作，重復一次以后，請幼兒重復主試的動作，并詢問幼兒“接下來應該怎么做”，然后請幼兒用不同的方式表示這個規律;主試做完兩個有規律的動作以后，請幼兒做出與主試不一樣的規律動作。

3. 視覺的模式：包括重復性模式（ABC）和發展性模式（ABABBABBB）。①ABC結構的模式：主試擺出“圓形—正方形—三角形—圓形—正方形—三角形—圓形—正方形—三角形”規律的模式（不同色，且顏色沒有規律），請幼兒擺出這個模式，并詢問幼兒“接下來是什么”，最后請幼兒使用不同的方式表示這個規律;②ABABBABBB結構的模式：主試擺出“兔子—胡蘿卜—兔子—胡蘿卜—胡蘿卜—兔子—胡蘿卜—胡蘿卜—胡蘿卜”（同色），請幼兒擺出這個模式，并詢問幼兒“你知道接下來應該擺什么嗎？”，然后請幼兒使用不同的方式表示這個規律;幼兒看完兩個規律后，主試請幼兒用兔子和胡蘿卜的圖片擺出自己的模式。

（四）測查計分

行動研究之初，研究者對60名幼兒的模式能力進行了前測，利用spss22.0軟件分析大班幼兒的得分情況以及大班幼兒在模式活動中的表現和特點。然后歷時4個月，研究者又對幼兒進行了后測，以探究經過行動研究，實驗班幼兒的模式能力是否發生變化。主試根據幼兒在測查中的表現進行評分，在模式復制、模式擴展任務中采用“0、1”計分，“0分”表示不能完成任務，“1分”表示能夠完成任務。在模式創造、模式轉換任務中采用累積計分，即只要兒童創造或轉換出一種形式，就計1分，分數可以累計;如果一種都無法創造或轉換，則計0分。

這里需要說明的是，前后測的題目結構、難度都一樣，只是稍微變化了一下呈現的材料，比如前測時使用的是雪花片，后測則改為小木塊。前測使用的是小兔子和胡蘿卜，后測使用的則是小狗和骨頭。又由于前后測時間相差4個月之久，所以避免了練習效應。

三、研究結果與分析

（一）量的分析

1. 大班幼兒模式前測得分總體情況。

根據大班幼兒（60名）在前測中完成任務的得分情況可以得出，模式總分最高分為27分，最低分為1分，平均分為10.78分，標準差為5.906。在對幼兒模式得分進行正態分布檢驗時（見圖1），得出偏度系數Skewness=0.792，峰度系數Kurtosis=0.309，兩個系數都小于1，可認為近似正態分布。由此可以看出，本次測查工具的難度適宜大班的幼兒。

2. 不同模式類型的前測得分情況。

在對60名大班幼兒的前測中，幼兒在不同知覺、不同模式能力以及不同模式結構的得分情況詳見表4：

由表4可知，在各項知覺方面，幼兒動覺的模式平均分最高，而視覺和聽覺的平均分則相同;在模式的各項能力方面，幼兒的復制能力平均分最高，其次是模式擴展能力，然后是模式創造能力，模式轉換能力的平均分得分最低，這也就說明幼兒缺乏表征模式的能力;在模式結構方面，幼兒的重復性模式平均分最高，而發展性模式得分較低。

3. 實驗班與對照班的幼兒在前后測中的得分情況。

由表5可以得出，將對照班幼兒、實驗班幼兒的前后測模式得分進行配對樣本t檢驗，發現在行動研究的4個月內對照班幼兒的模式能力無顯著變化（P=0.292>0.05），這意味著傳統的模式教學方式在促進大班幼兒模式能力的發展上效果不明顯。而實驗班幼兒在行動研究的前后測查中有顯著性差異（P=0.000<0.001），這表示了經過三輪的行動研究干預，幼兒的模式能力獲得了明顯提升，也意味著多元表征教學的有效性。

注：前測中N=30;后測中個別幼兒流失：實驗班N=28，對照班N=27;*P<0.05，**P<0.01，***P<0.001（下同）

4. 實驗班與對照班幼兒在前后測中的模式水平對比。

由下頁表6可以得出，在前測時，兩個班級的幼兒模式水平無明顯差異（P=0.116>0.05），即在行動干預之前，兩個班的幼兒模式發展水平接近。而在實驗班經過三輪行動干預、對照班進行常規的模式教學活動后，發現兩班幼兒的模式水平出現了明顯差異（P=0.000<0.001）。因此，與傳統的模式教學相比，多元表征教學能夠更好地促進大班幼兒模式能力的發展。

（二）質的分析

經過三輪行動研究干預后，研究者對實驗班幼兒的表現進行了質性分析：每天記錄下兒童和實驗班教師的行為表現，并收集行動小組教師的反思日志。最后，從一手資料中，編碼出幼兒和教師通過行動研究發生的改變。

1. 兒童的變化。

（1）認知方面——“模式創造與轉換”方面更加勝任。

從前測數據可知，兒童的模式復制和擴展能力發展較好，而模式創造和轉換能力相對較差，這體現了模式能力發展的遞進性，即在模式的各項能力中，模式識別是基礎，隨后發展起來模式的復制、擴展、創造、轉換能力。雖然模式的創造和轉換能力發展對幼兒來說較有挑戰，但是在幼兒早期的模式學習中，模式的創造和轉換能力都體現了幼兒思維的靈活性。[23]因此，在進行模式活動設計的時候，研究者重點關注培養幼兒的模式創造和轉換能力，幼兒在行動研究過程中也獲得了此方面的發展。例如，在區域活動中，幼兒在用動物貼畫來做出自己的模式時，某幼兒提議說可以用筆把自己的模式表示出來，于是其他幼兒也開始嘗試用符號來表示自己的模式;在集體活動中，當幼兒自由選擇材料進行表征時，有的幼兒會根據自己的喜好主動要求使用樂器（教師未事先提供），當教師提供之后，會主動和其他幼兒結伴使用不同的樂器表現某種模式。這些都體現了在行動研究過程中，幼兒在模式識別的基礎上，已經初步獲得了模式創造和轉換的意識與能力。

（2）行為方面——在生活中主動運用模式。

兒童在行為方面的變化表現為實驗班的幼兒逐漸能夠將模式知識與生活聯系起來。隨著行動研究的逐漸深入，幼兒的行為開始發生了一些變化，比如幼兒開始主動地用模式裝飾自己的作品（繪畫作品、相框等）;能夠關注到生活中有規律的事物（如樓梯、柵欄）;在區域活動時能夠自己提出用另外一種方式表示同一模式;在閱讀和其他的自由活動中，幼兒能夠主動使用模式去解決問題。

戶外活動時間，有的幼兒在跳繩，而忘記帶跳繩的幼兒則用粉筆在地上畫畫，地上有圓圈且均勻地劃分為幾個部分，有個幼兒說要裝飾成一個大蛋糕，在裝飾的過程中，幼兒用不同的顏色填充不同的空間，并且顏色的排列有自己的規律（最內圈是一個紅色大圓點，第二圈是黃藍模式，第三圈是白綠模式，第四圈是粉色重復模式）。

———2017年10月19日，行動小組成員A

（3）情感方面——樂在其中地“學習”。

在幼兒的情感方面，表現為幼兒對參與模式活動的興趣提高。在第一輪行動研究的時候，研究者一直在重復AB這一模式，這導致在第一輪后期，幼兒參與AB型規律活動的興趣有所下降。為了提高幼兒在活動中的興趣，在第二輪行動研究時，研究者增加了模式結構的多樣化;在第三輪行動研究的時候，增加了更多的活動形式，比如動畫片、繪本、貼畫、手指謠等，這都使得幼兒在游戲的過程中獲得了模式能力的發展。

在區域活動中，當教師將貼畫投入到美工區以后，美工區幼兒的數量迅速增加，最多的時候有8個幼兒同時進入到美工區，他們有的用貼畫創造自己的模式，有的用筆畫出的符號表示模式。在《亂七八糟的魔女之城》活動結束以后，研究者將繪本投入到閱讀區，在自由閱讀時間，幼兒開始爭先恐后地去閱讀這本書，閱讀過程中，幼兒一邊認真地看故事中的情節，一邊尋找這本書中的模式，并與同伴交流。在研究者播放動畫片《嗚咪123》時，出現模式內容幼兒也能夠投入到劇情里面，跟隨動畫片的要求，解決動畫片中模式的問題，如在第2集中嗚咪兄妹在尋找拉繩時，需要小鳥們唱一首特別的歌“啾啾—滋滋—啾啾—滋滋—啾啾—滋滋”，當一個小鳥不會唱時，為了幫助小鳥，幼兒會主動跟著一起有規律地唱這首歌;在第34集中，為了從果醬中救出小雞，需要幼兒教小雞朝一個方向有規律地移動，即“扭扭—扭扭—拍打—扭扭—扭扭—拍打”，幼兒們都很開心地晃動自己的身體教小雞如何移動。這些都體現了幼兒對模式活動濃厚的興趣。

2. 行動小組成員的變化。

（1）態度認知方面。

在對教師進行訪談的時候，發現幼兒園教師在數學教學中很少開展多元表征教學，其主要原因集中表現為以下兩個方面，一是教師本身對多元表征教學不了解，不愿意使用多元表征策略進行教學;二是使用多元表征需要教師投入更多的時間和精力去設計教學活動，因此，有些教師就會選擇使用單一的教學方式。基于以上這種情況，行動研究的重點就是我們不斷學習和討論如何有效地實施多元表征教學，包括閱讀相關理論、頭腦風暴、辯論、總結。

從第一輪的摸索到第二輪的艱難轉變，再到第三輪的真正多元，我們看到了幼兒對多元表征教學活動的喜愛，看到了他們模式能力的提高，尤其是幼兒在模式轉換能力上（多元表征方面）的提升。在這個過程中，行動小組的教師對多元表征教學的態度也都發生了變化。

在最開始聽到“多元表征”的時候，我是很懵的，因為我以前沒有聽過這個概念，也不知道在教學中如何使用多元表征策論。隨著行動研究的進行，我漸漸改變了看法，這才發現除了傳統的、單一的知識點教授，教師也可以使用更多的方式和途徑進行教學，所以，在以后的教學中，我會盡量采用多元表征的教學策略。

——2017年11月17日，實驗班教師C

（2）教學能力方面。

行動研究是一個動態過程，在這個過程中，能夠鼓勵教師“深入觀察教學動態，仔細分析學生的行為和互動情況，驗證挑戰現有的實踐慣例，敢于嘗試新的教學方法”，[24]即使在這個過程中，教師遇到了失敗，也是有實際的借鑒意義的。在前兩輪的行動研究過程中，雖然行動小組的教師在實施多元表征模式教學活動的時候遇到了困難，但是經過一次次并不完美的嘗試后，研究者和行動小組教師吸取經驗并積極調整教學活動，最終走向了多元表征的教學活動。在這個過程中，我們對如何運用多元表征進行模式教學進行了多次實踐，從開始的單個模式結構到后來的多樣模式結構，從開始的單一模式難度到后來有層次的任務提供，從開始的單一集體教學干預到后來對區域、生活活動的干預，從開始過于注重核心經驗的傳授，到后來對游戲性、情境性更加關注……這些摸索，使我們更加深刻地了解了多元表征教學策略的意義，掌握了多元表征教學開展的步驟，同時也期待著更多多元表征的策略運用到其他領域的教育實踐中。

四、討論與教育建議

（一）討論

經過四個月的行動研究干預，無論在量的方面，還是在質的方面，實驗班幼兒的模式能力都獲得了提升，從而驗證了多元表征教學的有效性。這種有效性不僅體現在后測分數的顯著性提高，還體現在幼兒對模式概念的熱情，幼兒能主動把模式概念運用于生活，行動小組成員對多元表征教學策略不再“抵觸”，運用多元表征教學策略的能力得到了提高。下面對本研究能夠取得成效的原因嘗試作總結：

1. 行動研究方案設計合理，實施中不斷反思。

行動研究是針對實踐中的問題而進行的研究，具有“反饋—調整性”的特點，即研究者可以根據實踐中發生的情況對活動的目標、結果和手段進行調整。[25]在本研究中，行動研究方案的設計目的是為了解決當前模式教學中表征單一的問題而嘗試探索多元表征的教學策略。

首先，我們根據前測結果，設計了初始方案，干預的重點放在了模式創造與轉換這兩個方面，并依據文獻與實踐情況，把多元表征確定為動覺、視覺、聽覺三個層面。其次，我們針對行動研究中出現的問題，隨時討論調整。美國教育家波斯納曾指出，“沒有反思的經驗是狹隘的經驗，至多只能成為粗淺的知識”，[26]在行動研究實施的過程中，行動小組教師會在每一輪活動結束后及時針對活動中方案的設計、教師的教學表現、幼兒的表現三個方面進行反思，討論并撰寫反思日志，反思日志的撰寫可以幫助行動研究者“返回去”尋找觀念的根據、“跳出來”思考自己的行為和觀念，這些都有助于行動研究中的教師對當前的活動進行反思，在總結經驗的基礎上，進行下一次教育活動。[27]比如當我們發現單一AB結構不利于調動兒童的興趣增強對模式概念的掌握時，隨即增加了其他結構;發現區域與生活活動無法與多元表征的集體模式教學形成合力時，則對區域和生活活動進行了干預;發現我們過于重視模式核心經驗的傾向時，則加入了對幼兒過程性能力獲得的關注;等等。

2. 行動小組協同合作。

行動研究既可以是個人的，也可以是多人協同合作的。本研究采用的是多人合作模式，由學前教育專業研究生、實驗班教師、大學教師共同構成行動小組。協同合作的形式，可以集思廣益，為行動研究方案的制訂、實施、討論與反思提供多維度的思路，同時，高校研究者的參與可以為行動研究提供理論上的指導。[28]

在行動研究實施的過程中，行動小組成員共同制訂干預計劃，然后由學前教育研究生A實施行動。期間，A與三位實驗班教師針對每節活動及時討論并撰寫反思記錄。在每一輪行動研究結束后，A與大學教師E共同針對本輪行動研究的優點和不足進行反思，以便在下一輪行動研究中進行改進。四個月的行動研究結束后，行動小組的教師在對多元表征教學的態度上更加積極主動，同時，運用多元表征教學的能力也有所提升。

（二）教育建議

1. 幫助幼兒理解數學的關系并能夠選擇恰當的方式進行表征。

數學是一門高度抽象的學科，學前階段的幼兒處于具體形象思維階段，對數學中的內在邏輯關系的理解較為困難，而多元的表征方式可以通過縱向、橫向、縱橫相結合呈現數學概念的形成過程，有助于學生理解數學概念的本質內涵，把握數學概念的外延特征，實現數學概念的科學建構。[29]但是，已有相關研究還表明，在學某些數學概念時，不適宜的表征形式并不能幫助幼兒解決數學問題，反而會增加幼兒認知學習的負擔。[30]因此，教師在進行教學時，應根據教學內容去選擇適宜的表征方式，不能一味地“求多”。比如《音樂會》這個活動中，既有音樂（聽覺表征），又可以非常自然地加入隨音樂而起的動作表征。但是，在《亂七八糟的魔女之城》這個活動中，因為這是一節繪本閱讀活動，注重幼兒在活動過程中對繪本內容的理解程度，所以這節活動更適合視覺上的表征，如果一味求多，則會對幼兒的理解造成障礙。

2. 在日常生活中注重對幼兒多元表征意識的培養。

黃瑾（2011）指出學習者通過學習多元表征，可以在兩種或多種不同的表征形式之間進行轉換，這有助于學習者對某一概念的完整架構，對學習內容的含義也將有更深的理解。[31]但是，幼兒數學多元表征能力的培養，不能僅僅通過幾節集體活動就實現，更需要教師能夠在日常生活（區域活動、生活環節等）和其他領域活動中，抓住教育契機，創設多元表征的任務。比如在戶外排球的時候，教師就可以引導兒童有規律地拍球，在音樂活動中引導幼兒發現音樂中蘊含的聽覺模式等。

跳出模式概念的多元表征，從更廣泛的兒童表征來看，幼兒往往會選擇自己擅長的方式去表征問題，這就需要教師在幼兒表征的基礎上，鼓勵幼兒嘗試其他形式進行表征問題，如游戲“你劃我猜”中對身體動作的觀察、天秤游戲中用各種符號記錄結果、用身體動作表征母雞蘿絲走過的路線等，都體現了數學概念的不同表征形式。總之，教師應該在各類活動以及游戲中鼓勵幼兒運用多感官去感受數學的概念，并嘗試用多元的方式將概念表征出來，以促進幼兒數學思維的發展。

3. 關注幼兒數學過程性能力，從而促進幼兒數學概念的理解與運用能力。

數學能力分為內容性能力和過程性能力，內容性能力是大家較為熟悉的數概念與運算、集合與分類、模式、幾何與空間等關鍵概念的獲得。數學過程性能力描述的是學生知道如何學習、理解和應用數學的能力，它強調的是“獲得和運用知識的方法”。[32]這一過程性能力對幼兒終身學習、數學素養的養成和數學概念的獲得都至關重要。[33]

我們的行動研究在第三輪干預中，著重關注了幼兒數學過程性能力的培養，因為諸多研究證實，教學中對學生數學過程性能力的關注，是兒童獲得數學內容知識的有力支撐，它能夠提高學生對某個概念的理解能力，從而提高數學學業表現。[34][35]之所以如此，是因為兒童在面臨一個數學問題時，會激發他們之前儲存的數學知識，并激發他們運用多種策略。在這個過程中，兒童會回憶、練習、運用數學內容性知識。[36]與此同時，在問題解決過程中，兒童去探索一個未知的問題，情感是好奇的、積極的。[37]當我們引導兒童關注某個數學概念與生活之間的關聯時（數學關聯能力），他們會不自覺地把自己的興趣置于實際情景的應用中，[38]不僅讓他們認同數學的有用性，還會在實際情景中更好地理解抽象數學概念。

然而，在教育實踐中，一線教師往往對其關注不夠。[39]望本行動研究能夠在一定程度上引起教師們對幼兒數學過程性能力的關注。在數學活動中，不僅要心存數學內容知識方面的“關鍵概念”，還要關注兒童的問題解決能力、推理驗證能力、數學交流能力、數學表征能力及數學關聯能力。

參考文獻：

[1]史亞娟，龐麗娟，陶沙，等.兒童數學認知能力發展的影響[J].心理發展與教育，2003（4）：47-51.

[2]LYNN M， MCGARVEY. Is it a pattern？[J]. Teaching Children Mathematics，2013（5）：564-571.

[3]MARINA M， PAPIC J T， MULLIGAN M C， et al. Assessing the development of preschoolers mathematical patterning[J]. Journal for Research in Mathematics ?Education，2011（3）：237-268.

[4]姜慧慧.義務教育階段學生數學表征能力的測評[D].上海：華東師范大學，2014：5-6.

[5][39]周晶.5～7歲兒童數學過程性能力的構成要素及應用研究[D].上海：華東師范大學，2016：60-63.

[6]唐劍嵐.數學多元表征學習及教學[M].南京：南京師范大學出版社，2009：45.

[7]章佳穎.4～6歲兒童數學認知中多元表征研究[D].上海：華東師范大學，2011：11-21.

[8]張亞杰.提高幼兒園數學模式的有效性[J].上海托幼，2012（3）：12-13.

[9]黃瑾，田方.學前兒童數學學習與發展核心經驗[M].南京：南京師范大學出版社，2015：59-60.

[10]杜青霞.高中生數學概念多元表征的調查研究[D].武漢：華中師范大學，2014：3-12.

[11]HRAGREAVES A. Transforming knowledge： blurring the boundaries between research， policy， and practice[J]. Educational Evaluation and Policy Analysis，1996，18（2）：105-122.

[12]ELLIOTT J. Action research for educational change[M]. Milton Keynes： Open University Press，

1991：78.

[13]HO C L . An investigation of preschool teachers ways of seeing action research using phenomenography[J].Educ Res Policy，2016（15）：147-162.

[14]陳向明.質的研究方法和社會科學研究[M].北京：教育科學出版社，2000：448.

[15]孫楊麗.運用多元表征教學策略進行中班幾何圖形教學的行動研究[D].天津：天津師范大學，2014：9-17.

[16]李子彪.行動研究及其推廣的意義[J].廣州教育，1992（6）：16-20.

[17]周蔥蔥，林泳海.3.5～6.5歲兒童式樣認知發展的實驗研究[J].心理學探新，2003（1）：33-36.

[18]黃瑾.幼兒園數學教育與活動設計[M].北京：高等教育出版社，2010：163-164.

[19]史亞娟，龐麗娟，陶沙，等.3～5歲兒童模式認知能力發展的研究[J].心理發展與教育，2003（1）：46-51.

[20]楊崢崢.4～5歲兒童模式與排序能力發展的研究：城市與農村兒童的比較[D].上海：華東師范大學，2007：5-12.

[21]高燕.小班幼兒模式認知能力及其培養研究[D].南京：南京師范大學，2009：5-45.

[22]陸敏.多元表征學習在幼兒園數學活動中的應用研究[D].上海：華東師范大學，2013.

[23]周欣，黃瑾，郭力平，等.我國學前兒童數學監測指標體系的構建[J].學前教育研究，2018（10）：12-21.

[24]MILLS G E.教師行動研究指南[M].重慶：重慶大學出版社，2010（3）：11-12.

[25]洪明.行動研究與幼兒教育[J].學前教育研究，2001（4）：27-29.

[26]范曉文.讓教師成為研究者：淺談反思能力的培養[J].科學咨詢（教育科研），2006（11）：59.

[27]楊宏偉.幼兒教師怎樣進行行動研究[J].教育與教學研究，2004（6）：14-15.

[28]楊云秀.農村幼兒教師環境創設能力提升的行動研究[J].教育與教學研究，2014（6）：124-128.

[29]席愛勇.數學多元表征：讓概念形成過程“看得見”[J].教育研究與評論，2017（9）：65-67.

[30]唐劍嵐.國外關于數學學習中的多元外在表征的研究述評[J].數學教育學報，2008，17（1）：30-34.

[31]黃瑾.論學前兒童數學學習中的多元表征[J].全球教育展望，2011（1）：60-62.

[32]National Council of Teachers of Mathematics. Principles and standards for school mathematics[R]. Reston，VA：NCTM，2000：29.

[33]周晶.5～7歲兒童數學過程性能力構成要素探索與模型建構[J].學前教育研究，2018（2）：12-24.

[34]NUNES T， BRYANT P， BARROS R， et al. The relative importance of two different mathematical abilities to mathematical achievement[J]. British Journal of Educational Psychology， 2011（82）：136-156.

[35][38]MARIA A S， KONSTANTINOS Z. Building meaning through problem solving practices： the case of four-year olds[J]. The Journal of Mathematical Behavior， 2014，35：58-73.

[36]ZACHAROS K， KOUSTOURAKIS G. A critical approach to school mathematical knowledge： the case of realistic problems in Greek primary schooltextbooks for seven-year-old pupils[J]. Acta Didactica

Napocensia，2011，4（1）：39-51.

[37]SHIAKALLI M A， ZACHAROS K. The contribution of external representations in pre-school mathematical problem solving[J]. International Journal of Early Years Education， 2012，20（4）：315-331.

An Action Research on Promoting the Development of 5～6-year-old Childrens Pattern Ability Using Multi-dimensional Teaching Strategies

Yingchun Zhang，1 Juan Li，2，3 Tong Shen，4 Hongling Zheng，5 Lihong Wang，5 Ying Li5

（1College of Education and Art， Shangqiu Institute of Technology 476000 China; 2College of Teacher Education， Wenzhou University，Wenzhou 325035 China; 3Department of Education， Hebei University ?071000 China; 4Beijing Normal University Kindergarten， Beijing 100875 China; ?5Qingnian Lu Kindergarten， Baoding，071000 China）

Abstract： Pattern ability is an important mathematical ability in early childhood. It is an important prerequisite for children to form logical thinking， and it lays a good foundation for childrens future mathematics learning and development. This study adopted an action research paradigm， and used multi-representational teaching strategies to intervene in experimental classes of young children （30）. The action research lasted for four months. The scope of intervention included group activities and regional activities. The researchers performed a group activity once a week， with four rounds of activity and a total of three rounds （12 collective activities）. After one semester of intervention， we examined the childrens pattern ability ?before and after（60） to explore the influence of multi-representation teaching strategies on the development of childrens model ability， and analyze the effectiveness of multi-dimensional representation teaching strategies. The study found that： after the three rounds of action studies were completed， the childrens pattern ability improved both quantitatively and qualitatively. In terms of quantity， childrens pattern ability in the experimental class has improved significantly， both in comparisons of children before and after the test， or in comparison with the control class. In terms of quality， the children of the experimental class are more competent in the creation and transformation of the pattern， and they can apply the concept of the pattern to life; the teachers of the experimental class no longer “contradict” the multi-representation teaching strategy， and the ability has been improved. In addition， the study also discussed the reason of this action research why was effective， and we believed that reasonable programs and team members collaboration are key factors for effectiveness. Finally， we proposed educational advices： Help young children understand the relationship between mathematics and choose the appropriate way to represent; Pay attention to the cultivation of childrens multi-representation consciousness in daily life; Childrens process ability should get more attention in practice.

Key words： pattern ability， multi-representation， action research