基于三次曲線模型CFG樁復合地基中性點位置計算

郅 彬，李 戈，武李和樂，郭 潔，任 興

(1.西安科技大學 建筑與土木工程學院，陜西 西安 710054；2.西安建筑科技大學 土木工程學院，陜西 西安 710055；3.陜西省建筑設計研究院有限責任公司，陜西 西安 710018)

CFG樁復合地基在地基加固中取得了良好的工程效益[1]，但其作用機理尚不清楚，而探究機理的關鍵一步在于獲取較為準確的中性點位置.由于中性點位置目前尚無直接獲取有效準確方法，故已有研究成果對于中性點位置的獲取多采用理論研究的方法[2-7].目前對中性點位置的理論研究中，假定樁側摩阻力隨深度的變化曲線多采用簡化的直線代替，與實際有較大的誤差，存在一定的局限性.

本文將樁側摩阻力隨深度的變化關系用三次曲線方程z=kτ3+C代替，考慮樁土變形協調，建立平衡方程，推導出CFG樁復合地基中性點位置的表達式，依據現場CFG樁復合地基靜載荷試驗數據，計算得出中性點具體位置.依據現場CFG樁復合地基高應力靜載荷試驗數據與表達式進行對比，并探究不同褥墊層厚度與樁徑對中性點位置的影響，討論其影響機制.

1 基本原理與公式推導

1.1 基本假定

①樁側摩阻力隨深度的關系變化曲線為三次曲線方程z=kτ3+C，其中，z為土體深度，τ為樁體側摩阻力.

②單元體法向位移為零且不考慮側面剪力；

③不考慮樁體的徑向變形.

1.2 建立計算模型

當CFG樁承擔上覆載荷產生向下運動趨勢或位移時，樁體受到土體方向向上的側摩阻力，稱為正摩阻力.反之，當樁土之間產生沉降差，即樁相對于土體有向上運動或向上運動趨勢時，則樁體受到土體提供的負摩阻力.負摩阻力與正摩阻力相等的點稱之為中性點.中性點位置所對應的負摩阻力為零，在z=0處樁體與樁間土相對位移最大，因此該處負摩阻力最大，最大負摩阻力參考Berrum 公式.摩阻力表達如下:

τ0=Ktanφσs+c

(1)

式中：φ為樁周土體內摩擦角，c為黏聚力，K為土體被動土壓力系數，σs為樁間土表面豎向應力，可由文獻[5]得到.

(2)

假設樁體側摩阻力變化曲線方程為z=kτ3+C，則

(3)

其中：l0為中性點深度，τ(z)正值時，表示正摩阻力，τ(z)負值時，表示負摩阻力.

樁側摩阻力隨深度變化如圖1所示：

圖1 樁身摩阻力隨深度變化曲線圖Fig.1 Diagram of friction resistance of pile body with depth

如圖2所示，在某深度z處取樁間土微單元體，列豎向平衡方程，即

σszAs-(σsz+dσsz)As-τ(z)updz=0

(4)

其中：σsz為中性點以上某深度z0處土體應力，As為單元體樁間土面積，up為樁體橫截面周長.

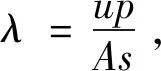
(5)

將式(3)代入上式求解，得

(6)

將邊界條件z=0，σsz=σs代入式，可解得C1=σs，代回式，得

(7)

圖3 CFG樁微元體Fig.3 microelement of CFG pile

如圖3所示，在中性點以上某深度z處取樁體微單元體，列豎向平衡方程.

σpzAp-(σpz+dσpz)Ap+τ(z)updz=0

(8)

其中：σpz為樁某深度z處樁身應力；Ap為樁身截面積.

(9)

將式(3)代入式(9)，得

(10)

將邊界條件z=0σpz=σp代入式(10)，可解得C1=σp，代回式(10)可得：

(11)

1.3 中性點位置的確定

由式(7)，得樁間土中性點以上變形量Ss上與中性點位置以下變形量Ss下，即

(12)

(13)

式中，Es為樁間土壓縮模量，由于土層性質不同，取各層土的加權壓縮模量，即

(14)

式中，Es1、Es2、…、Esx為各土層的壓縮模量，l1、l2、…lx為各土層厚度.

CFG樁在墊層中刺入深度δ1依據下式計算.

δ1=cu(σp-σs)

(15)

cu為樁頂作用于褥墊層的豎向刺入量.

(16)

其中，Lc為褥墊層厚度，Ec為褥墊層模量.

下臥層樁端入刺深度δ2采用下式計算.

δ2=cd(σp1-σs1)

(17)

其中，cd為樁端在下臥層的豎向刺入量.

(18)

其中：μ0為樁端泊松比，K為樁端土體的基床系數，Ad為CFG樁底面積，w為沉降影響系數，結合文獻[6]取0.97，E0為樁端土壓縮模量，σp1，σs1表示樁端與樁間土.

考慮樁土協調變形，樁間土壓縮量等于CFG樁身刺入褥墊層與下臥層之和，故有

Ss上+Ss下=δ1+δ2

(19)

將式(12)，(13)，(15)，(17)帶入式(19)，可解得中性點位置l0.

1.4 CFG樁復合地基極限承載力確定

由于褥墊層多為砂礫碎石構成，故不考慮褥墊層黏聚力對承載力的影響，利用太沙基承載力系數簡化樁頂作用力qu1.

qu1=γ1LcNq+γ1dNγ

(20)

式中，Nc、Nq、Nr為承載力系數，可查閱太沙基承載力系數圖得出.

Nc=(Nq-1)cotφ；

Nγ=[(Kpγ/2cos2φ)-1]tanφ/2；

依據文獻[6]，pu2為樁端作用力，等于樁端土的不排水抗剪強度與樁的承載力系數Nc2乘積.

(21)

其中，Nc2為樁承載力系數，本文取Nc2=9. 取樁體微單元體為研究對象，對樁體中性點上下部分積分，得到樁體側摩阻力公式.

(22)

當樁頂先于樁端破壞時，即

qu=qu1+T

(23)

當樁端先于樁頂破壞時，即

qu=qu2+T

(24)

CFG樁復合地基極限承載力公式為

qu=min(qu1+T,qu2+T)

(25)

2 計算公式驗證

以西安市高新技術產業開發區某工程為背景.選取21 m試樁3個，樁徑0.4 m，樁間距1.5 m，編號分別取SZ1，SZ2，SZ3.加載試驗前將150 mm厚中粗砂均鋪至復合地基表面，并安裝圓形剛性承壓板.本次靜載試驗以混凝土堆積重物為反力，加荷設備為630 t油壓千斤頂，第一級加荷為240 kPa，后每級增加120 kPa壓力至1 200 kPa，再以每級60 kPa壓力遞增至1 800 kPa，進行高應力靜載荷試驗.根據土工室內試驗及勘察報告，確定土層及材料基本物理力學參數，見表1.

表1 物理力學參數值Tab.1 parameter values of physical mechanics

將試驗參數帶入式(19)可得，中性點l0=4.24 m， 查太沙基公式承載力系數表得，Nq=43，Nγ=41.

其中：qu1=γ1LcNq+γ1dNγ

=23×0.15×43+23×0.4×41

=526.5 kPa；

qu2=c′uNc2

=70×9=630 kPa；

]=832.61 kPa.

其中，樁側摩阻力可由式(1)、(2)、(14)、(16)聯立求得，由式(25)得：

qu=min(1 359.11,1 462.61)=1 359.11 kPa

復合地基靜載荷試驗結果如下所示.

圖4 高應力作用下復合地基p-s曲線Fig.4 p-s curve of composite foundation under high stress

如圖4所示，當荷載加至到1 300 kPa時，SZ3所對應曲線開始出現拐點，沉降變形增加明顯，當沉降變形量增至上一級沉降變形量的2倍時，停止加載試驗，SZ3對應荷載1 620 kPa.SZ1與SZ2所對應曲線為緩變型，當其沉降量超過40 mm時，分別對應荷載值1 740 kPa和1 800 kPa.此時承壓板周圍褥墊層出現側向擠出現象；依據相關規范，判定此時復合地基已經破壞，中止加載.綜合三組試驗，得到該場地CFG樁復合地基極限承載力為1 720 kPa.

對比試驗與計算結果，計算結果與試驗誤差率為26.5%，分析原因為計算模型建立需設定一系列假定條件，增大了誤差；同時由于現場試驗時在褥墊層厚度及模量設置上各試驗樁不可避免的存在差異，導致計算結果與試驗存在誤差，但整體誤差未超過30%，說明了該模型的合理性.

3 中性點的影響因素分析

本文取褥墊層厚度和樁徑為變量，基于式(19)探究對中性點位置的影響.

3.1 褥墊層厚度對中性點位置影響及分析.

褥墊層厚度分別選擇150、250、350、450、550 mm，其余參數參考現場試驗數據.

圖5 不同褥墊層厚度對中性點位置的影響Fig.5 Effect of cushion thickness on the neutral point position

如圖5所示，隨著褥墊層厚度增加，中性點位置深度也隨之增加，但幅度趨于平穩，最終穩定在5.7 m.分析原因為：褥墊層厚度變大，增加了褥墊層流動補償能力，樁間土受力增加，使其沉降量增加，同時CFG樁向上刺入褥墊層，樁土沉降差變大，負摩阻力增強，中性點位置下移.隨著褥墊層厚度增加，受荷時褥墊層被壓密，CFG樁向上刺入程度減弱，樁土沉降差趨于穩定，負摩阻力增長緩慢，中性點位置趨于平穩.

3.2 樁徑對中性點位置的影響及分析

CFG樁樁徑分別選擇0.3、0.4、0.5、0.6、0.7 m，其余參數參考現場試驗數據.

圖6 不同樁徑對中性點位置的影響Fig.6 Influence of different pile diameter on the position of neutral point

如圖6所示，隨著樁徑的增加，樁身處中性點位置深度也隨之增加，但增加幅度趨于平穩，其位置深度穩定在5.5m左右.分析原因為：當樁徑較小時，CFG樁刺入褥墊層相對容易，此時樁向上刺入褥墊層量較大，樁土沉降差較大；但隨著樁徑的增加，CFG樁刺入褥墊層的難度增加，刺入量的增加值減小，樁土沉降差趨于穩定，負摩阻力增長緩慢，中性點位置趨于平穩.

4 結論

(1)將樁側摩阻力隨深度關系變化曲線用三次曲線方程z=kτ3+C代替，考慮樁土變形協調，建立平衡方程得出CFG樁復合地基中性點位置表達式與極限承載力表達式.依據現場復合地基高應力靜載荷試驗，與試驗結果進行對比，證明表達式的合理性.

(2)利用所得表達式探究不同褥墊層厚度與樁徑對中性點位置的影響，結果表明：隨著褥墊層厚度與樁徑的增加，中性點的深度先增加，后逐漸趨于穩定.