無言的結局
2019-08-13 10:15:00張小漁
數理化解題研究 2019年21期
關鍵詞:方法
張小漁
(江蘇省蘇州國際外語學校 215000)
代數題,在求解時有的比較繁瑣、有的比較困難.如果我們換一種思路,通過挖掘其隱含的幾何背景,構造出符合題意的幾何圖形,解答往往極其簡單、直觀.請看以下幾例.
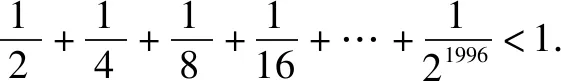
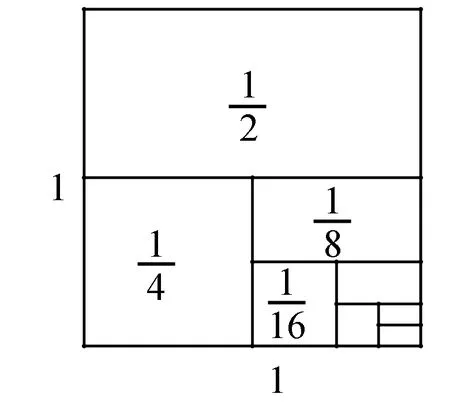
圖1
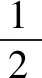
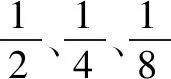
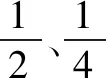
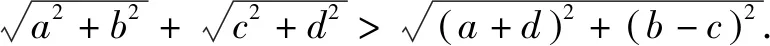
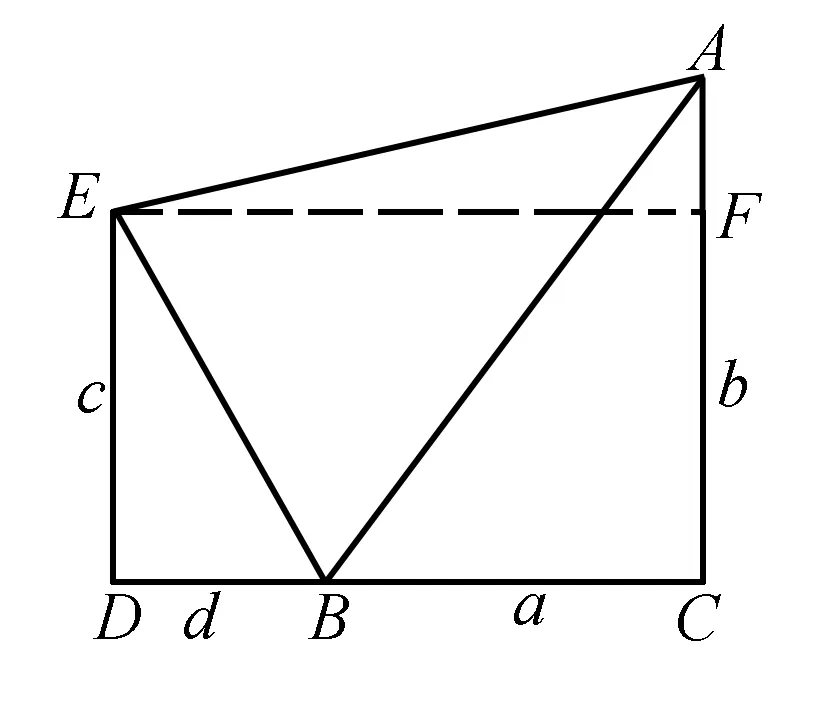
圖2
分析本題從解不等式的角度,必須經過兩次運算推理,繁瑣是免不了的.若能把根式反映成直角三角形的斜邊的長,本題的三個二次根式就轉化為三角形三邊長,也就不難求證了.
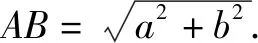
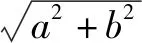

圖3
例3已知方程x2-px+rs=0(p、r、s都是正實數),且p2-4rs≥0,試用幾何方法求方程的根.
分析要求方程的兩根,由于兩根之積為rs反映成幾何圖形就是圓中的切割線定理或相交弦定理,那么如何構造兩根之和呢?如果借助兩線段和及中點坐標公式問題就迎刃而解了.
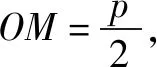
評注本題從一個全新的角度讓我們認識一元二次方程的根,只要制作精度較高的直角坐標系,對于x2-px+rs=0的方程,當其中的p2-4rs≥0,且p>0,r>0,s>0,根據p、r、s的讀數,也就相應得到方程兩個根的近似值的讀數.
本題的求解讓我們學到如何處理兩數和與積的構圖方法.
著名的勾股定理的證明方法多達300余種,大多數是利用構造圖形來證明的.下面我們一起欣賞一下美國第十二屆總統加菲爾德的證明.
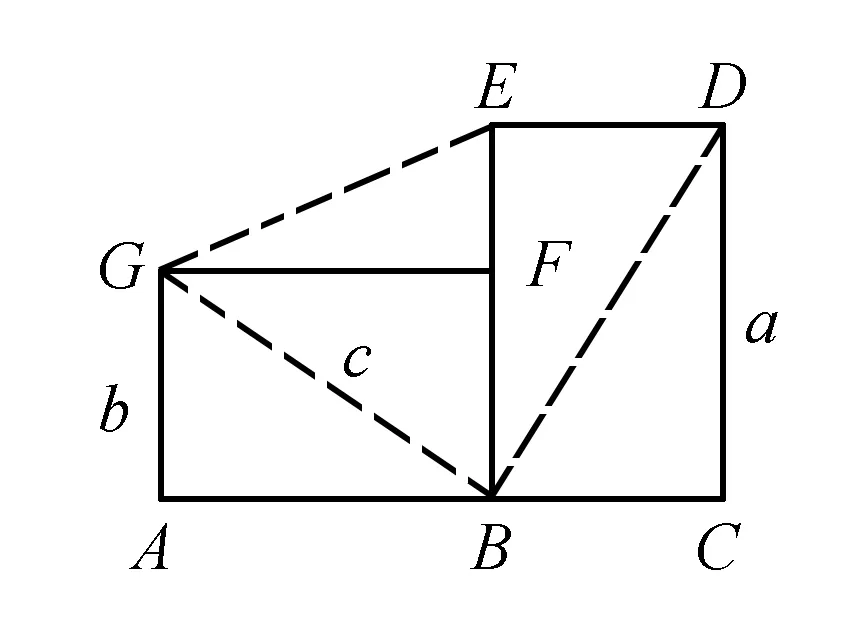
圖4
例4如圖4,構造兩個全等的矩形顯然有:
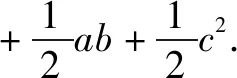
綜合得a2+b2=c2.
人們戲稱,美國總統踢倒一塊磚頭便證明了勾股定理.
猜你喜歡
中老年保健(2021年9期)2021-08-24 03:52:04
河北畫報(2021年2期)2021-05-25 02:07:46
中學生數理化(高中版.高考理化)(2020年2期)2020-04-21 05:33:04
兒童繪本(2020年5期)2020-04-07 17:46:30
兒童故事畫報(2019年5期)2019-05-26 14:26:14
Coco薇(2016年2期)2016-03-22 02:42:52
山東青年(2016年1期)2016-02-28 14:25:23
Coco薇(2015年1期)2015-08-13 02:47:34
小雪花·成長指南(2015年7期)2015-08-11 15:03:12
小雪花·成長指南(2015年4期)2015-05-19 14:47:56

