面向彈道優化的高超聲速再入飛行器模態穩定性分析

雍恩米，劉深深，程艷青，錢煒祺,2

1. 中國空氣動力研究與發展中心 空氣動力學國家重點實驗室，綿陽 621000 2. 中國空氣動力研究與發展中心 計算空氣動力研究所，綿陽 621000

升力式再入飛行器以高超聲速再入地球大氣層時，面臨著復雜的臨近空間力熱環境，各類大氣環境參數以及氣動參數的不確定性對其再入運動具有較大影響，較小的擾動可使其偏離預定軌跡較大甚至逸出大氣層，導致航天任務的失敗。飛行器自由擾動運動的穩定性分析，可為飛行器總體設計、控制律研究等方面提供重要參考。已開展的穩定性研究工作主要集中在航空器的動力學穩定性分析以及航天器中彈道式再入飛行器如導彈、返回飛船的姿態穩定性分析[1-3]，而對于升力式高超聲速再入飛行器在臨近空間的動力學系統穩定性的研究相當有限。

從公開發表的文獻看，關于升力體飛行器的高超聲速動力學穩定性研究最早出現在20世紀中葉。Etkin研究了再入航天器的動力學穩定性問題,將經典的飛行器縱向動力學理論擴展到高速軌道飛行，研究了有動力升力體飛行器在大氣層邊緣的圓軌道上的攝動運動,該項研究中保留了運動方程中的行星曲率、引力梯度和以高度為自變量的大氣密度項，這些項在低速低高度飛行器的動力學穩定性研究中通常被忽略[4]。Vinh和Laitone研究了航天飛機滑翔再入的縱向動力學穩定性問題，引入無量綱時間變量，推導出了迎角的二階線性微分方程，針對兩種特殊情況，一是彈道式再入，二是小彈道傾角滑翔再入，求得了近似解，分析得出俯仰力矩導數是影響穩定性的主要因素[5]。文獻[6]研究了帶動力的吸氣式高超聲速飛行器長周期動力學穩定性，發現推力-馬赫數曲線的斜率對長周期模態的影響較大，另外還提出了基本反饋控制策略，即采用速度和高度反饋回路來改善不穩定特性。Stich等研究了高超聲速巡航飛行器的長周期特性和相關的飛行品質問題，在NASA的飛行仿真器上分析了馬赫數10條件下的長周期模態的不穩定特性和發動機時間延遲對操縱品質的影響。針對不穩定的長周期動力學特性，推導了新的操縱品質判斷準則[7-9]。Robert研究了超聲速巡航縱向動力學穩定性，分析得出推力和氣動外形對超聲速巡航飛行穩定性影響較大，采用高度和速度反饋有利于巡航高度保持[10]。Lael和Darryll針對上升、穩定巡航和周期性巡航3種任務，研究了乘波體高超聲速巡航飛行器縱向穩定性[11]。

國內關于升力式高超聲速飛行器模態穩定性分析的研究較少。賈子安等研究了乘波體飛行器縱向靜穩定特性，給出了有利于縱向靜穩定的乘波體形狀特征[12]。陳琛等針對升力體構型的高超聲速飛行器穩定性問題，在高超聲速飛行器的建模、靜穩定性分析、自由擾動模態穩定性3個方面進行較深入的研究，其中模態穩定性分析針對特征點，且縱向運動主要關注短周期模態特性[13]。李銳研究了高超聲速飛行器軌跡優化方法以及橫航向穩定性判據，分析了給定外形高超聲速飛行器在整個速度范圍內的橫航向穩定性[14]。蘇二龍和羅建軍研究了滑翔式高超聲速飛行器大迎角橫側向失穩問題，采用延拓算法和分岔理論求解，對平衡分支的穩定性和突變點進行了分析[15]。高清和李潛對美國典型高超聲速飛行器橫側向穩定性進行了分析[16]。葉友達等研究了類HTV-2高超聲速飛行器滾轉運動的穩定性以及滾轉運動的失穩判據[17]。

本文研究了面向彈道優化問題的高超聲速飛行器縱向模態穩定性，即針對無動力再入的高超聲速飛行器，考慮大氣密度隨高度的變化和引力梯度，分析高超聲速飛行器自由擾動運動的縱向穩定性，即縱向模態穩定性，并基于不同最優彈道的穩定性分析結果，提出對高超聲速飛行器彈道優化設計的建議。

1 高超聲速飛行器再入縱向運動模型

針對再入高超聲速飛行器運動特性和彈道穩定性分析的需求，考慮地球為非旋轉圓球時，飛行器無動力再入縱向動力學方程為[5]

(1)

(2)

(3)

(4)

(5)

θ=γ+α

(6)

式中：V、γ、q、r、θ、α分別為飛行器速度、航跡角、俯仰角速率、地心距、俯仰角和迎角；m為飛行器質量；Ix、Iy、Iz為主慣量矩；S為氣動參考面積；l為參考長度。主要運動參數如圖1所示，其中L、D、W分別為飛行器所受升力、阻力和重力，x軸為飛行器體軸縱向對稱軸。大氣密度ρ、引力加速度g是隨高度變化的函數。氣動力系數包括升力系數CL、阻力系數CD和俯仰力矩系數Cm。上述氣動系數是高度h、馬赫數Ma和迎角α的函數,即

(7)

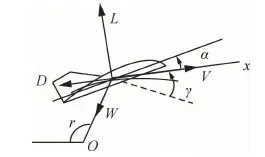
圖1 縱向運動主要參數示意圖Fig.1 Sketch map of main parameters of longitudinal motion

2 縱向動力學方程小擾動線性化

為分析高超聲速飛行器的模態穩定性，即自由擾動運動的穩定性，引入基準運動和小擾動運動的概念，建立小擾動運動方程，使運動方程線性化，然后獲得狀態方程和轉移矩陣，在此基礎上進行沿彈道的縱向模態分析。

首先根據式(2)、式(5)、式(6)得到關于迎角的微分方程，即

(8)

對式(1)～式(4)和式(8)進行小擾動線性化，得到

(9)

(10)

(11)

(12)

(13)

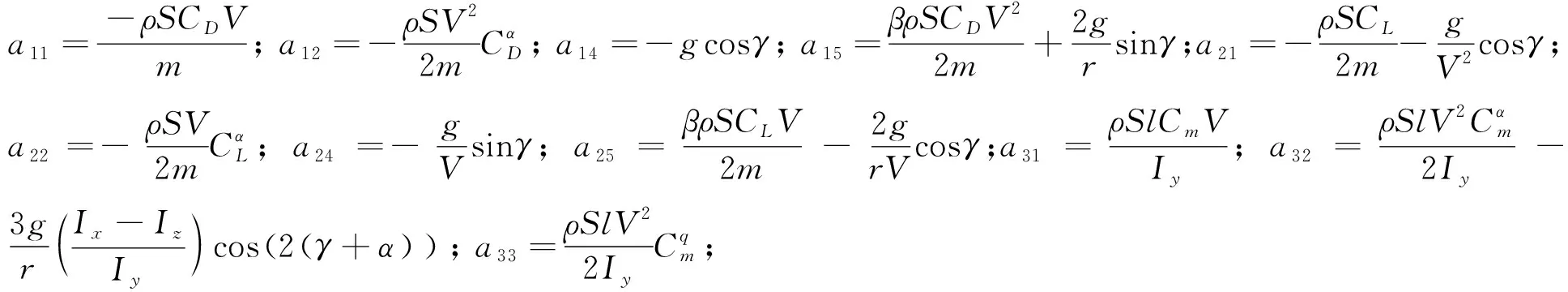
縱向運動方程小擾動線性化過程中采用的大氣密度模型為指數模型，即

ρ=ρ0e[-β(r-R0)]

(14)

式中：β為指數大氣密度常數；R0為地球平均半徑。因而有大氣密度對地心距的導數為

(15)

引力模型采用平方反比模型，即

(16)

從而得到引力對地心距的導數為

(17)

(18)

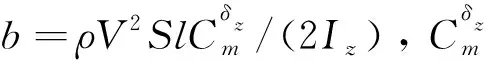
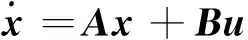
(19)

那么縱向擾動運動的穩定性可以由求解特征方程D(s)=|sI-A|的特征根進行分析。

3 高超聲速飛行器氣動特性分析

為開展高超聲速飛行器模態穩定性分析，還需要獲得飛行器氣動力數據。本文以美國高超聲速飛行器HX(Hypersonic X-plane)為背景，進行類HX氣動布局設計，利用二次曲線及基于類型函數和形狀函數的CST(Class function and Shape function Transformation technique)方法[18-19]，提出類HX升力體飛行器氣動外形布局，其計算網格如圖2所示。最后采用工程估算方法獲得飛行器的氣動力特性數據。

圖2 飛行器計算網格Fig.2 Computational grid for vehicle

由于高超聲速飛行器飛行空域范圍較大，因此對于不同流區，采用了不同氣動力工程計算方法。其中連續流區采用了修正牛頓理論。背風面修正利用Prandtl-Meyer公式，該類方法已經在高超聲速飛行器計算中得到了廣泛應用[20-21]，其精度基本滿足彈道設計與穩定性分析的精度要求。自由分子流區的氣動特性則采用碰撞模型進行計算，而稀薄流區氣動特性則采用當地化方法，連續流和自由分子流氣動力系數通過橋函數得到。

基于上述方法，得到了高超聲速飛行器在不同高度、馬赫數、迎角和側滑角下的氣動特性。本文研究高超聲速飛行器的彈道穩定性，因此主要考慮縱向氣動力特性，圖3給出了典型狀態下的升力系數、阻力系數和俯仰力矩系數隨迎角和舵偏角的變化曲面。

基于工程估算方法獲得飛行器的氣動力特性數據，進行縱向氣動數據配平，可以進一步分析該高超聲速飛行器的升阻特性。圖4為給定迎角為10°，不同高度條件下升阻比隨馬赫數的變化曲線。圖5為給定馬赫數條件下，不同高度升阻比隨迎角的變化曲線。分析圖4、圖5的結果可知：① 該飛行器在典型狀態下，最大升阻比在2.4～2.5左右，屬于高升阻比高超聲速飛行器；② 該飛行器的最大升阻比迎角約為10°,在第4節模態分析設計典型彈道的標準迎角剖面時，可以此為依據，即給定標準迎角剖面應盡量發揮升阻比的優勢；③ 在 給定高度條件下，該布局的高超聲速飛行器升阻特性隨迎角變化較大，而隨馬赫數變化較小，特別是飛行速度在馬赫數10～20這個范圍內。在設計高超聲速飛行器再入典型彈道時，可以利用該特性，對所采用的氣動力模型進行簡化和建模，即主要考慮迎角變量對升阻特性的影響。

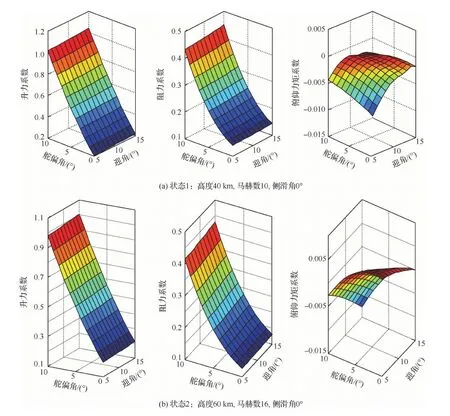
圖3 典型狀態縱向氣動力特性Fig.3 Longitude aerodynamic characteristic on typical states

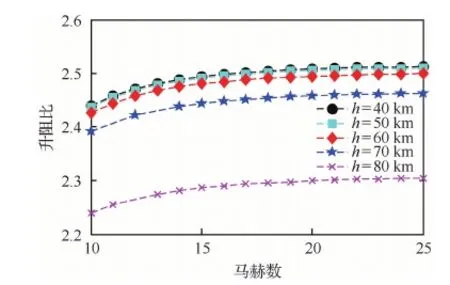
圖4 升阻比隨馬赫數的變化Fig.4 Variation of lift-to-drag ratio with Mach number

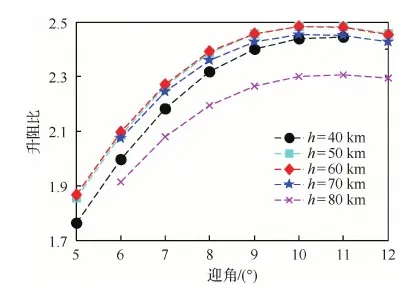
圖5 升阻比隨迎角變化Fig.5 Variation of lift-to-drag ratio with angle of attack

4 典型彈道模態穩定性分析

4.1 優化彈道模態

優化計算得到最大射程彈道高度和馬赫數變化曲線如圖6(a)所示，其飛行時間為3 423 s，射程為18 343 km。最小射程彈道如圖6(b)所示，其飛行時間為1 500 s，射程為7 606 km。

為從穩定性角度分析不同極限彈道的特性，這里分別計算了最大、最小射程彈道的模態特性，即沿彈道求解特征方程的特征根。早期關于高超聲速飛行器縱向長周期運動的研究表明，當考慮大氣密度隨高度的變化時，高超聲速飛行器相較于一般速域的飛行器，增加了一個長周期模態，即高度模態，同時也存在兩個常規模態，即沉浮模態和短周期模態。本文通過模態分析，同樣也得到3種模態和對應的5個特征根。

首先，分析最大射程彈道模態穩定性。由于5個特征根中的一個實根與其他4個根的數量級相差較大，因此模態圖分別在兩幅圖中畫出，分別對應一個實根與其他4個根。最大射程彈道對應的根軌跡如圖6(c)和圖6(e)所示。圖6(e)為一個大實根對應的模態，即高度模態，根軌跡基本位于負實軸上，這表明高度模態是穩定的且呈現非周期、快速衰減特性。圖6(c)中一對位于復平面左半平面的共軛復根對應短周期模態，即表征迎角和俯仰角速率的自由擾動穩定性變化。該短周期模態頻率沿彈道呈現由低到高變化的趨勢，且在再入初始階段，由于動壓較低，短周期模態的頻率與長周期模態頻率相當。圖6(c)中位于復平面實軸附近的兩個根為沉浮模態，該模態對應的根軌跡在實軸附近。在再入初段，沉浮模態為一對穩定的共軛復根，進入中段和末段，沉浮模態變為兩個實根，且趨于不穩定。圖6(d)和圖6(f) 為最小射程彈道模態分析圖。類似的，圖6(f)為最小射程彈道高度模態圖，與最大射程高度模態相比最大射程具有更大的負實根，說明對應的狀態衰減更快。圖6(d)為最小射程彈道短周期模態和沉浮模態圖：其中短周期模態也是穩定的，其頻率由小變大再變小；最小射程彈道的沉浮模態與最大射程彈道有相似特性，不同之處在于其位于左半平面的實根數目明顯增多，即沿最小射程彈道，穩定的沉浮模態特征根增多。

表1 彈道條件和過程約束Table 1 Conditions and process constraints of trajectory

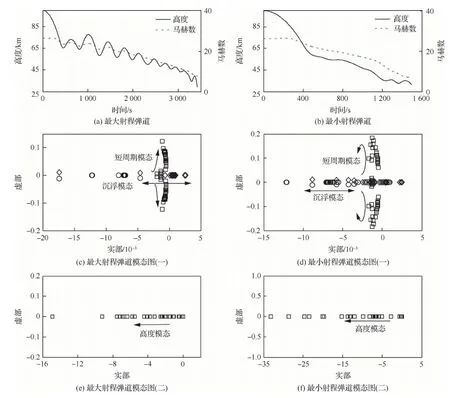
圖6 優化彈道模態分析Fig.6 Modal analysis of optimal trajectories

4.2 無約束跳躍彈道模態

前面分析了考慮過程約束的最大、最小射程彈道的模態特性，為了對比分析更多形式的高超聲速再入彈道模態特性，本節計算了不考慮路徑約束的最大射程彈道和無約束跳躍彈道，并進行模態穩定性分析。

上述兩種彈道的計算方法為：不考慮過程約束的最大射程彈道仍采用文獻[22]的優化方法，只是無動壓等過程約束，初始條件和終端約束同表1，計算得到該彈道飛行時間為3 926 s，射程為22 144 km，其高度、馬赫數曲線如圖7(a)所示。而無約束跳躍彈道直接生成，初始高度速度同表1，初始彈道傾角由0°改為5°，以實現彈道在高度空間的大幅度跳躍，其側傾角為取0°，即升力朝上，迎角仍采用標準彈道迎角剖面，結束條件為高度下降到30 km。跳躍彈道高度、馬赫數曲線如圖7(b)所示，飛行時間為4 859 s，射程為27 732 km。

兩種彈道的模態特性如圖7(c)～圖7(f)所示。兩種彈道的高度模態均為負的大實根，且跳躍彈道的高度模態衰減更快。無過程約束最大射程彈道與考慮約束的最大射程彈道相比較，射程增大了約18%，但沉浮模態的不穩定狀態增多。跳躍彈道與考慮約束的最大射程彈道相比，射程增加了約33%，但短周期模態出現了不穩定點，位于正實軸上，對應彈道為初始上升段。跳躍彈道的沉浮模態沒有出現共軛復根，均位于實軸上，且大部分都位于復平面右平面不穩定區域。

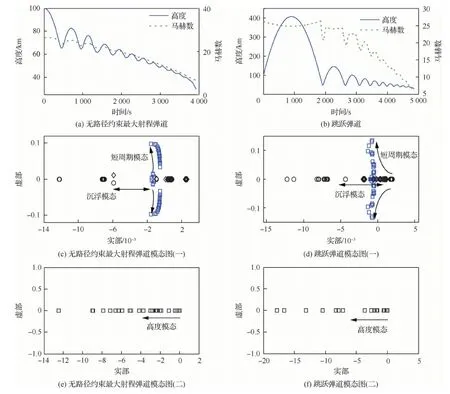
圖7 兩種無約束彈道模態分析Fig.7 Modal analysis of two types of unconstrained trajectories

綜合分析4條典型彈道(圖6、圖7)的模態特性可以得出以下結論：① 當考慮大氣密度隨高度變化時，高超聲速再入飛行器具有兩個長周期模態，即高度模態和沉浮模態，且高度模態為穩定的非周期模態;② 考慮過程約束的最大射程彈道和最小射程彈道都具有穩定的短周模態，且最小射程彈道穩定的沉浮模態特征根更多。

從無約束最大射程彈道和跳躍彈道的模態分析結果來看，高超聲速再入飛行器，在高度范圍內跳躍變化雖然能夠在很大程度上增大射程，但同時會使短周期模態和沉浮模態產生更多不穩定特征根。因此，從穩定性的角度，可以對彈道設計提出建議：應避免所設計的彈道產生太大的跳躍，即使是犧牲一些射程上的性能。

4.3 最大射程彈道典型狀態

前面分析了典型彈道的模態特性，現選取其中最大射程彈道上的再入初段、滑翔段和再入末段的3個狀態點作為典型狀態(見表2)，給出具體的特征根并進行穩定性分析。典型狀態點對應的模態特征根和無阻尼自振頻率見表3。分析表3 可知：再入初段短周期和長周期模態的頻率都比較低，沒有明顯的短周期和長周期區別；滑翔段短周期模態頻率明顯增大，沉浮模態由穩定的復根變為兩個實根，且有一個為不穩定實根，高度模態變為大的負實根；再入末段，短周期模態和高度模態無阻尼自振頻率繼續增大，且都是穩定的。

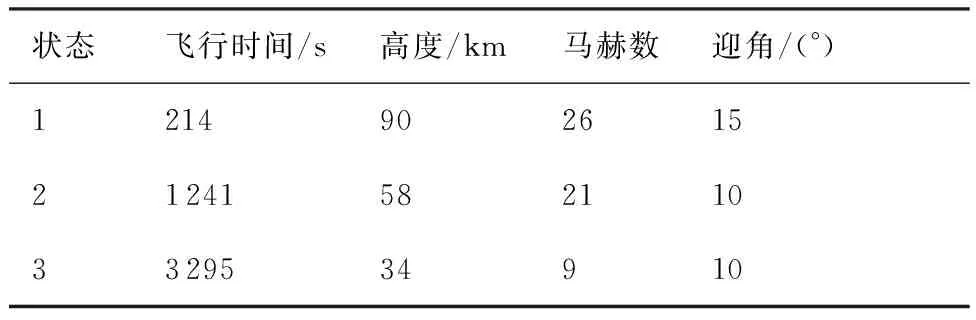
表2 典型飛行時刻狀態參數Table 2 State parameters of typical flight time

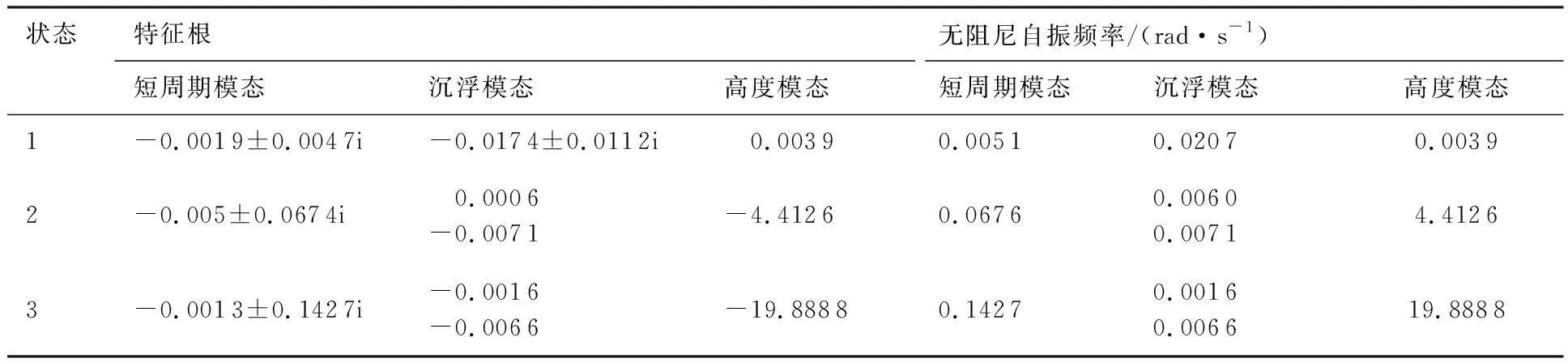
表3 典型飛行時刻特征根及頻率Table 3 Eigen values and frequencies of typical flight time

5 結 論

本文分析了高超聲速再入飛行器的縱向模態穩定性。引入基準運動和小擾動運動概念，建立無動力再入縱向動力學小擾動運動方程，然后獲得狀態方程和轉移矩陣，在此基礎上進行沿彈道的縱向模態分析。針對最大射程彈道、最小射程彈道和跳躍彈道以及最大射程彈道典型狀態的模態分析，得出以下結論：

1) 再入初段短周期模態和長周期模態的頻率都比較低，沒有明顯的短周期和長周期區別。

2) 高超聲速再入飛行器具有兩個長周期模態，即高度模態和沉浮模態，且高度模態為穩定的非周期模態。

3) 考慮過程約束的最大射程彈道和最小射程彈道都具有穩定的短周模態，且最小射程彈道穩定的沉浮模態特征根更多。

4) 高超聲速再入飛行器，在高度范圍內跳躍變化雖然能夠在很大程度上增大射程但同時會使短周期模態和沉浮模態產生更多不穩定特征根。

高超聲速飛行器縱向模態分析，即自由擾動運動的穩定性分析可為飛行器總體設計、制導控制律研究等方面提供重要參考。