考慮分子轉動自由度的離散統一氣體動理學格式

姚博，張創，郭照立

華中科技大學 煤燃燒國家重點實驗室，武漢 430074

多尺度流動在工程應用中廣泛存在，例如臨近空間飛行器、微機電系統(Micro-Electro-Mechanical System,MEMS)等問題中，同一個計算域內會同時存在連續流、滑移流甚至是自由分子流等不同流域，局部努森數可能相差數個量級[1]。在稀薄流中，基于連續介質假設的Navier-Stokes方程不再成立。常規求解Boltzmann方程的計算格式往往采用算子分裂方法[2-4]，存在時間步長小于平均碰撞時間、網格尺寸小于分子平均自由程的限制。而多尺度問題中連續流的存在，使得直接使用這類方法計算整個流場消耗相當巨大。

多尺度流動問題的直觀解決方法是將不同求解器耦合起來。在局部努森數較大的計算區間中求解Boltzmann方程，在局部努森數較小的計算區間中求解Navier-Stokes方程[5-6]。但準確劃分不同流域、合理地將不同流域耦合起來都很困難。近年來，基于動理學理論發展出的一類漸進收斂(Asymptotic Preserving, AP)格式[7]，使得同一個算法處理整個多尺度問題成為可能。其中，Xu等提出的統一氣體動理學格式(Unified Gas Kinetic Scheme,UGKS)[8-10]采用有限體積形式，在計算網格界面通量時采用控制方程在時間上的局部積分解，耦合了粒子間的碰撞與遷移過程，能夠準確描述連續流到稀薄流流域的流動問題。Guo等提出的離散統一氣體動理學格式(Discrete Unified Gas Kinetic Scheme,DUGKS)[11-13]也采用有限體積形式，繼承了UGKS的主要優點，但與UGKS也存在明顯的不同。在構造界面通量時，DUGKS采用的是沿特征線積分得到的數值解，計算效率更高[14]。

在實際的多尺度流動問題中，氣體往往是多原子氣體，如空氣的最主要成分是氧氣和氮氣2種雙原子氣體。氧氣和氮氣的轉動特征溫度分別為2.07 K和2.88 K，因此即使在室溫下其轉動能也能被充分激發出來。而由于振動特征溫度具有較高的值(氧氣與氮氣分別為2 256 K和2 719 K)，只有達到較高的溫度振動能才會被激發[15-17]。Rykov模型[18]就是考慮了分子平動和轉動自由度的動理學方程，能適用于較大范圍的雙原子氣體流動問題研究。近年來，不少工作基于Rykov模型方程研究了雙原子氣體流動問題[19]。例如Rykov等[20-22]先后計算了雙原子氣體的正激波結構和微管道內的流動；Liu等[23]構造出了基于Rykov模型方程的統一UGKS，計算的正激波結構、外掠平板等多個算例與直接蒙特卡羅(Direct Simulation Monte Carlo,DSMC)和實驗結果吻合良好；Wu等[24]將Rykov模型方程中的彈性碰撞項用Boltzmann碰撞項替換，并采用快速譜方法進行求解。

本文構造出了基于Rykov模型方程的離散統一氣體動理學格式，從單原子氣體拓展為計算考慮了分子轉動自由度的雙原子氣體，能夠有效模擬雙原子氣體從連續到稀薄的多尺度流動問題。

1 Rykov模型方程

Rykov模型方程考慮了氣體分子內部的轉動自由度，分別處理分子的彈性碰撞和非彈性碰撞[18]。氣體分子的速度分布函數記為f=f(t,x,ξ,η,e)，其中t為時間,x為空間坐標,ξ為分子在D維空間中的平動速度,η為分子速度在三維空間中的其他分量,e=M2/(2J)為分子轉動能，M為角動量，J為轉動慣量。宏觀量可以通過分布函數定義為

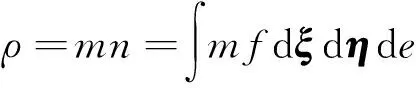
(1a)

(1b)

(1c)

(1d)

(1e)

(1f)

q=qr+qt

(1g)

式中:c為分子熱速度，c=ξ-U;k為玻爾茲曼常數;n為分子數密度;m為分子質量;U為流體速度;Tt和Tr分別為平動和轉動溫度;ε為分子轉動自由度對應的平均能量;qt為與平動自由度對應的熱流;qr為轉動能量傳輸產生的熱流;ρ為密度。

在不考慮外力項的情形下，Rykov模型方程中氣體分子速度分布函數f=f(t,x,ξ,η,e)的演化方程有如下形式：

(2)

式中:右側兩項分別表示非彈性碰撞項和彈性碰撞項。彈性碰撞項保持平動動能守恒，非彈性碰撞項則實現平動和轉動二者間能量的轉換。νt和νr分別為彈性和非彈性碰撞頻率；ft和fr分別為彈性碰撞項和非彈性碰撞項的平衡態：

(3a)

(3b)

(3c)

(3d)

式中:松弛時間τ=μt/pt,μt和pt分別為溫度Tt對應的動力黏度和壓力;T為平衡態溫度;參數Z反映單一轉動碰撞中平動碰撞發生的次數;D0為雙原子氣體的自擴散系數;ω0和ω1用于調整熱流qt和qr至合適的松弛值：

(4a)

(4b)

Rykov在文獻[18]中將分布函數對轉動能e求積，引入2個約化的分布函數，式(2)則轉化為2個關于約化后分布函數的方程。在D維問題中，分布函數的演化僅與D維的離散速度ξ有關而與η無關。為進一步消除分布函數對冗余變量的依賴，降低計算消耗，可采用類似的處理方法引入3個約化的分布函數

(5a)

(5b)

(5c)

則宏觀量可表示為

(6a)

(6b)

(6c)

(6d)

(6e)

(6f)

q=qr+qt

(6g)

式中:R為氣體常數。

分布函數f0、f1和f2的控制方程可對式(2)積分得到

(7a)

(7b)

(7c)

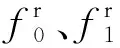
(8a)

(8b)

(8c)

(8d)

(8e)

(8f)

(8g)

(9a)

(9b)

(9c)

控制方程式(7)可以改寫為

(10a)

(10b)

(10c)

2 數值格式

本節基于式(10)構建考慮分子轉動自由度的離散統一氣體動理學格式。首先將其統一為

(11)

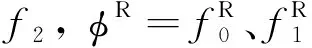
(12)

(13)

式中：Fn+1/2(ξ)為穿過網格界面的流量；Δt=tn+1-tn為時間步長；|Vj|和?Vj分別為控制體Vj的體積和表面積；dS為表面積；r為指向控制體表面外的單位法向量;φj和Ωj為單元上分布函數和碰撞項的平均值：

(14a)

(14b)

(15a)

(15b)

于是式(12)轉變為

(16)

由式(11)中碰撞項的守恒性可以得到

(17a)

(17b)

(17c)

(17d)

(17e)

(17f)

q=qr+qt

(17g)

計算界面流量Fn+1/2的關鍵在于獲得界面處原始分布函數fn+1/2。DUGKS采用在半個時間步長s=Δt/2內對式(16)沿特征線積分：

φ(tn+s,xb,ξ)-φ(tn,xb-ξs,ξ)=

(18)

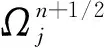
(19a)

(19b)

則式(18)可以寫為

(20)

其中：

(xb-xj-ξs)·σj，(xb-ξs)∈Vj

(21)

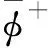
(22a)

(22b)

(22c)

(22d)

(22e)

(22f)

q=qr+qt

(22g)

通過tn+1/2時刻界面處宏觀量可以得到的相應的Rykov分布函數φR，依據式(19)得到原始的分布函數：

(23)

在上述推導中，分子運動速度ξ被認為是連續的。在實際計算中，需要將速度空間離散為速度集ξi(i=1,2,…,N)。離散速度集通常選為Gaussian-Hermite或Newton-Cotes等特定數值積分公式的節點坐標，上述積分需要被替換為數值積分。例如，對于守恒變量有

(24a)

(24b)

(24c)

(24d)

由于在重構界面分布函數時耦合了分子的碰撞和遷移過程，DUGKS具備漸進收斂特性。DUGKS中的時間步長由Courant-Friedrichs-Lewy (CFL)條件確定[11]：

(25)

式中:ζ為CFL數;Δx為最小網格尺寸;ξm為最大離散速度值;Um為最大流動速度。

對于定常流動問題，選取2個相鄰時間步中宏觀量場的平均變化比α作為計算收斂的判據:

(26)

式中:W∈{ρ,U,T}，當α小于給定的參考值時認為計算達到收斂。

Rykov模型方程中參數Z與旋轉碰撞數Zrot之間存在如下關系[24]:

(27)

其中，當計算雙原子時固定參數d=2。Zrot可采用Landau-Teller-Jeans轉動能量松弛模型[25]計算得到，即

(28)

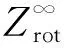
3 數值驗證

本節將采用數個雙原子氣體流動的問題驗證基于Rykov模型方程的DUGKS方法的正確性和有效性，包括一維氮激波結構、二維超聲速平板繞流、二維超聲速圓柱繞流和2個連通方腔中的跨流域流動等問題。

3.1 激波結構

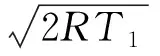
(29a)

(29b)

(29c)

(29d)

式中：Ma為上游馬赫數；Ma′為下游馬赫數。

計算域選為-25λ1≤x≤25λ1，并采用100個均勻分布的物理網格。速度空間取為-15≤ξ≤15，采用201個均勻分布的Newton-Cotes積分點。x≤0范圍內的分布函數初始值為上游參數確定的平衡態分布，x>0范圍內的分布函數初始值為下游參數確定的平衡態分布。平動溫度Tt和轉動溫度Tr的初始值與平衡態溫度T相等，即Tt1=Tr1=T1和Tt2=Tr2=T2。激波上下游邊界處分布函數分別固定為上下游宏觀量對應的平衡態分布。計算中CFL數均取為0.95，收斂判據為熱流的平均變化比小于10-8，即αq<10-8。

DSMC方法中取ZDSMC=3.5，DUGKS和UGKS當中Z=2.4，根據文獻[24]取參數δ=1/1.33,ω0=0.477以及ω1=1.919。分別比較了Ma=1.53、4.0、5.0和7.0 這4種馬赫數下的氮激波結構。圖1給出不同馬赫數下，DUGKS與文獻[23]中UGKS和DSMC的氮激波結構計算結果對比。圖1中均為歸一化后的宏觀量，以Q表示宏觀量，下標u和d分別表示上游和下游值，歸一化后為Q′=(Q-Qu)/(Qd-Qu)。可以看到，DUGKS與UGKS的計算結果在不同馬赫數下都吻合良好。二者計算的密度曲線與DSMC的結果吻合良好，溫度曲線則在激波上游位置上升得更早一些。產生這一差異的主要原因是DUGKS和UGKS采用的松弛模型只采用了單一的松弛時間，在靠近激波上游的位置將高速分子的能量平均分配給全部分子[12]。

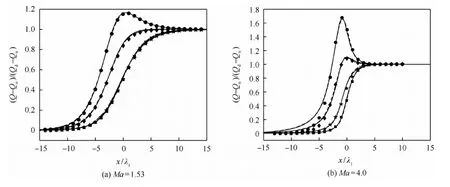
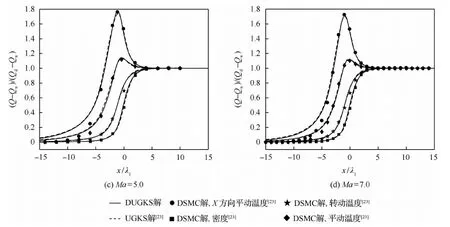
圖1 不同馬赫數下DUGKS、UGKS和DSMC的氮激波結構計算結果對比Fig.1 Comparison of nitrogen shock structure results of DUGKS, UGKS, and DSMC under different Mach numbers

3.2 超聲速平板繞流

飛行器在臨近空間飛行中以高超聲速飛行時，流場中存在激波-激波、激波-壁面的相互作用，飛行器表面附近會出現高熱流和高壓強的現象。

本算例取自Tsuboi和Matsumoto[26]的風洞試驗run34，Xu等[27]基于多溫度模型方程的氣體動理學格式，Liu等[23]基于Rykov模型方程的統一氣體動理學格式，先后對該問題進行了數值模擬。在run34試驗中，噴嘴出口馬赫數Ma=4.89，總溫T0=670 K，總壓p0=983 Pa，噴嘴出口溫度Te=116 K，密度ρe=6.15×10-5kg/m3。平板由金屬銅制造而成，試驗中通過水冷實現恒溫290 K。試驗氣體為氮氣，氣體常數R=297 J·kg-1·K-1，熱度系數ω=0.75。黏性與溫度之間關系為

(30)

式中：μ0=1.656×10-5Pa·s,T0=273.5 K。計算中采用硬球分子模型，平均自由程λ與黏性的關系為

(31)

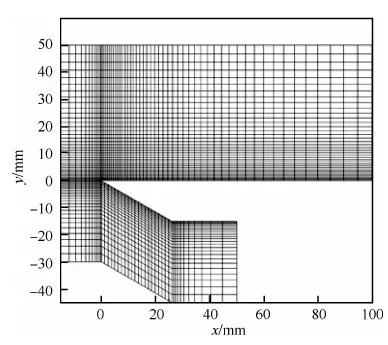
圖2 超聲速平板繞流計算網格Fig.2 Computational mesh for supersonic flow around flat plate

圖3(a)～圖3(d)分別為計算得到的密度、平均溫度、平動溫度以及轉動溫度云圖。可以看到，轉動溫度Tr升高滯后于平動溫度Tt。這一現象可以解釋為：高速的雙原子氣體與壁面碰撞后，宏觀動能轉換為分子熱運動動能，使平動溫度升高。經過分子間的相互作用，再傳遞給轉動溫度對應的內能。在平板上端x=5 mm和x=20 mm處沿坐標y方向上的溫度曲線在圖4中給出，計算結果與實驗數據、UGKS解總體吻合良好。

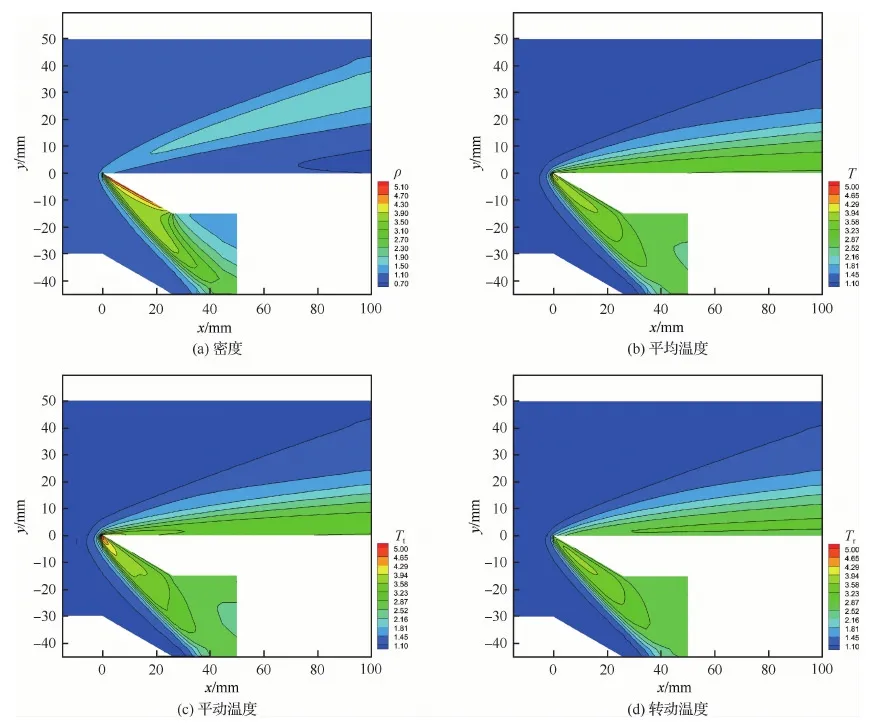
圖3 DUGKS計算的平板繞流密度、平均溫度、平動溫度和轉動溫度云圖Fig.3 Contours of DUGKS results around flat plate for density, equilibrium temperature, translational temperature, and rotational temperature

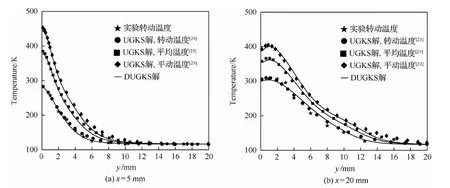
圖4 x=5 mm和x=20 mm處沿y方向溫度分布曲線對比Fig.4 Temperature plots along y direction at x=5 mm and x=20 mm

3.3 超聲速圓柱繞流

本算例進一步測試了氮氣的超聲速鈍體繞流問題，算例來源于文獻[23]。來流氮氣的速度U∞=1 684.5 m/s，溫度T∞=273 K，分子數密度n∞=1.299 44×1021/m3，動力黏度μ∞=1.657 88×10-5Pa·s，取熱度系數ω=0.75。圓柱表面為恒定溫度Tw=273 K。可計算出，來流氮氣馬赫數Ma=5.0，努森數Kn=0.1。

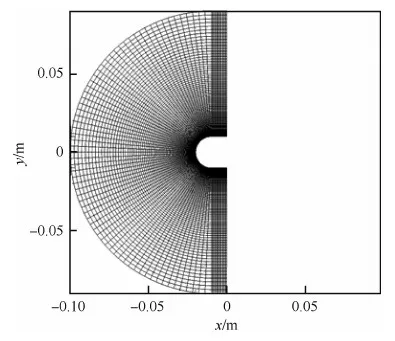
圖5 超聲速圓柱繞流計算網格Fig.5 Computational mesh of supersonic flow around a cylinder

圖6(a)～圖6(f)分別為DUGKS計算圓柱繞流的密度、x方向速度、y方向速度、平均溫度、平動溫度以及轉動溫度云圖。圖7顯示的是在y=0 m處沿x方向的參數曲線。可以發現，DUGKS計算的密度、速度曲線都與UGKS和DSMC結果吻合良好，而DUGKS和UGKS二者的溫度曲線比DSMC的計算結果上升地更早一些，這與前面的一維激波結構的研究結論是一致的。

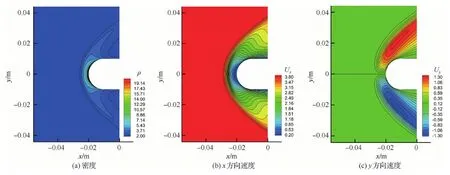
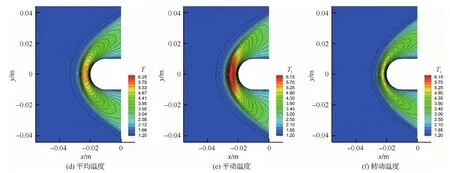
圖6 DUGKS計算的超聲速圓柱繞流流場云圖Fig.6 Contours of supersonic flow around a cylinder of DUGKS results

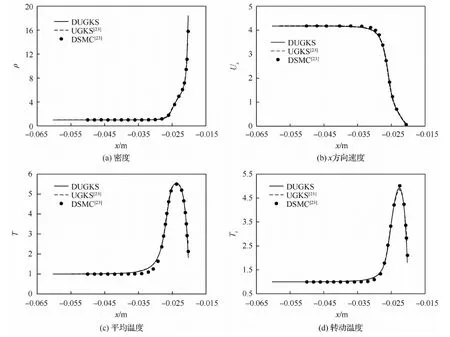
圖7 超聲速圓柱繞流在y=0 m位置的流場分布Fig.7 Flow distributions along line y=0 m for supersonic flow around a cylinder

3.4 兩個連通方腔中的跨流域流動

在太空探索中，火箭燃料罐爆裂或者宇航倉泄漏時，泄漏到太空中的氣體會經歷從連續流到自由分子流等不同流域的變化。高效地模擬跨流域流動對預測航天器泄漏等實際問題具有指導意義。本算例參照文獻[28]構造出了2個方腔中的跨流域流動，如圖8所示。方腔及管道中氣體為氮氣。方腔邊長為L=1 m，管道長為L，寬為H=L/8。初始狀態下，左、右兩個方腔分別維持在不同壓力，管道中間處的隔板將兩側氣體分開。兩側氣體溫度均為273 K，左側壓力pL=48.16 Pa，右側壓力pR=0.004 816 Pa。方腔及管道壁面均為恒定溫度Tw=273 K。可計算得到，左、右兩側的努森數分別為KnL=0.001和KnR=10，左側處于連續流域，右側接近自由分子流域。在t=0 s時刻，移去管道中的隔板，左側的氣體在壓力的作用下迅速噴入右側。

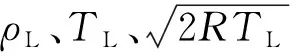
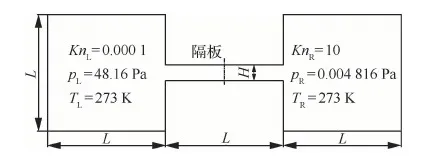
圖8 兩個連通方腔跨流域流動示意圖Fig.8 Schematic diagram of multiscale flow of two connected cavities

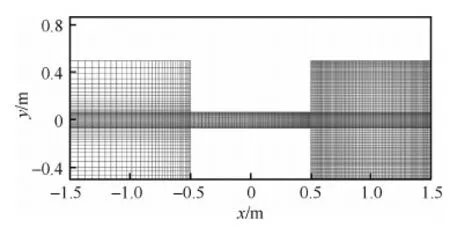
圖9 兩個連通方腔跨流域流動的計算網格Fig.9 Computational mesh of multiscale flow of two connected cavities

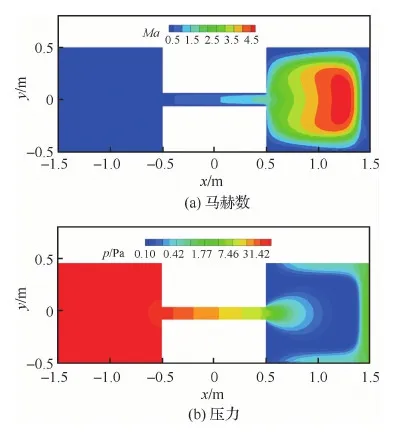
圖10 t/tc=1時馬赫數及壓力分布云圖Fig.10 Contours of Mach number and pressure at t/tc=1

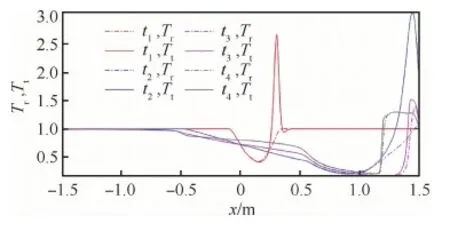
圖11 t/tc=0.09，0.5，1.0和2.0時刻沿中軸線(y=0 m)溫度分布曲線Fig.11 Temperature distributions along line y=0 m at time t/tc=0.09, 0.5, 1.0, and 2.0

4 結 論

基于考慮分子轉動自由度的離散統一氣體動理學格式，對激波結構、超聲速平板繞流以及超聲速圓柱繞流等算例進行計算，得到以下結論：

1) 基于Rykov動理學模型方程并采用Landau-Teller-Jeans轉動能量松弛模型的離散統一氣體動理學格式，可以反映出雙原子氣體非平衡流動時轉動和平動自由度對應的能量轉換過程，可用于計算雙原子氣體的多尺度流動問題。

2) DUGKS計算的結果與UGKS、DSMC的解以及實驗值吻合良好。其中，激波結構算例中馬赫數范圍從1.5變化到7.0，超聲速外掠平板以及超聲速圓柱繞流分別測試了DUGKS在帶有尖端的平板以及鈍體中的計算性能，驗證了考慮分子轉動自由度的離散統一氣體動理學格式的準確性及穩定性。

本文僅構造了考慮分子轉動自由度的離散統一氣體動理學格式并驗證了一維及二維算例，同時考慮分子振動自由度并將其應用于實際的復雜三維計算有待進一步研究。