雙重未知干擾解耦的多傳感器系統偏差校正與狀態估計

馮肖雪，李淑慧,*，潘峰, 2

1. 北京理工大學 自動化學院，北京 100081 2. 北京理工大學 昆明產業技術研究院，昆明 6501064

傳感器可以提供感興趣目標在時間和空間上的信息，因而在目標跟蹤、組合導航、容錯控制以及工業監控等領域應用十分廣泛，其中傳感系統的狀態估計問題日益引起人們的關注。但是在狀態估計過程中，由于系統參數的變動、大型系統中的相互耦合項、系統動態學中的非線性項、傳感器測量精度有限等因素引起系統建模模型誤差，往往影響狀態估計精度。一般而言，可將上述幾類引起建模誤差的因素統一視為未知干擾輸入。具有未知干擾輸入的隨機系統狀態估計問題廣泛存在于控制、通信、信號處理和故障診斷等領域。目前解決含有未知干擾輸入的隨機系統狀態估計問題的方法，大致可以分為以下幾類。

1) 狀態方程中含有未知干擾：文獻[1]針對直流電動機的狀態估計和故障診斷問題，通過解耦未知干擾輸入，借鑒遞歸濾波器的框架提出了魯棒的三步卡爾曼濾波算法，實現了最小方差無偏狀態估計和故障診斷。文獻[2]針對含有未知干擾、執行器和傳感器故障的離散線性系統，基于魯棒兩階濾波器估計狀態、生成觀測冗余，進而采用貝葉斯二值假設檢驗自適應地診斷故障。但上述方法為實現未知干擾解耦對故障反饋矩陣的秩有著嚴格的約束條件。文獻[3]針對狀態方程中含有未知干擾的線性時變隨機系統聯合狀態估計與故障診斷問題，通過將復雜不確定系統轉換為標準的帶故障和未知輸入的狀態空間模型，基于最小方差無偏準則提出了遞歸五步濾波器來估計系統的狀態和故障，該算法對于故障反饋矩陣的秩沒有任何約束限制，但估計結果并非最優。參考文獻[4]針對狀態方程含有未知干擾的不確定廣義系統，通過將未知干擾擴維到狀態向量中推導了最優遞歸濾波器，但是該方法計算量大，實時性無法得到保證。

2) 量測方程中含有未知干擾：文獻[5]針對傳感器含未知輸入和相關噪聲的離散隨機線性系統，設計了最小方差無偏狀態估計器，推導了任意兩個傳感器子系統之間的濾波誤差互協方差矩陣，給出了標量加權分布式融合狀態濾波器。文獻[6]研究了含有量測丟失和未知量測干擾的多傳感器隨機不確定性系統，設計了獨立于未知干擾的集中/分布式融合狀態估計器，但上述兩種方法均要求隨機干擾矩陣的秩不得超過傳感器量測維數。文獻[7]針對量測方程中含有未知干擾的線性時變系統設計了上界濾波器，通過凸優化求解濾波上界的極小值獲得了最優參數估計結果，但該方法要求量測新息協方差存在上界。

3)狀態和量測方程中均含有未知干擾：文獻[8] 將未知干擾簡化為均值和方差未知的高斯項，對未知干擾與狀態不獨立情況下的離散隨機系統提出了兩階期望最大化算法來辨識未知干擾。文獻[9]基于期望極大化方法提出了聯合狀態估計和未知輸入辨識的框架，用來計算系統未知輸入的條件期望，但該方法同樣假設未知干擾服從高斯分布。文獻[10]針對含有未知干擾的線性時變離散隨機系統，提出了擴維魯棒三階卡爾曼濾波對系統狀態和故障進行同時估計。文獻[11]針對含有未知干擾、執行器故障和傳感器故障的線性時變離散隨機系統的故障診斷和狀態估計問題，提出了改進的增廣魯棒三階卡爾曼濾波算法，但上述兩種算法均假設未知干擾建模為寬平穩過程的隨機游走噪聲。

總結來看，針對狀態和量測方程中含有未知干擾的狀態估計問題，目前的相關研究成果存在以下局限性：① 算法推導過程中對部分變量有著嚴格的假設或約束條件；② 通常假設未知干擾輸入具有高斯特性或者具有確定的分布特性；③ 通過歸并、擴維等方法對未知干擾進行估計，算法非實時、復雜度高。因此，很有必要研究狀態方程含有未知干擾(無任何先驗信息)、量測方程含有未知偏差(可視為一類特定的干擾)情況下的多傳感器在線狀態估計問題。

本文設計了適用于狀態方程含未知干擾、量測方程含未知偏差的多傳感器最小方差無偏估計濾波器。組織結構如下：第1節描述了狀態方程含未知干擾、量測方程含未知偏差的動態離散系統，并給出了本文研究的問題。第2節針對狀態方程含未知干擾、量測方程含有未知偏差的動態離散系統設計了雙重未知干擾解耦下的最小方差無偏估計濾波器。第3節給出了徑向飛行控制系統的仿真實例驗證了本文提出算法的有效性。第4 節對論文工作進行了總結。

1 問題提出

狀態方程和量測方程帶有未知干擾輸入影響的線性離散系統可描述為

xk+1=Akxk+Bkμk+ζk+Ekdk

(1)

yi,k=Ci,kxk+ηi,k+Di,kbi,k

(2)

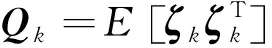
式(2)通過Di,kbi,k項來描述各種不同的傳感器量測建模不確定性。不失一般性，可以對未知的傳感器干擾或者偏差給出如下演化模型:

bi,k+1=Fi,kbi,k+vi,k+Gi,kui,k

(3)

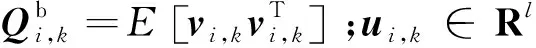
說明1 不失一般性，認為Ek為列滿秩矩陣。因為即便Ek不滿足列滿秩，依然可通過秩分解，Ekdk=E1,kE2,kdk，令第1項E1,k為列滿秩矩陣，而利用Ci,k+1來描述狀態模型所受的未知干擾輸入。通過Ekdk項除了可以描述加性干擾外，還可以用來描述各種不同的系統狀態建模不確定性，比如系統建模過程中的非線性項、線性化操作、模型降階簡化、以及參數變化等引入的誤差。

說明2 式(3)中定義的傳感器干擾或者偏差演變模型是普遍意義上的通用模型。若Fi,k=I,vi,k=0,Gi,k=0，則傳感器干擾或偏差為常值；若Fi,k=0,Gi,k=0，則傳感器干擾或偏差為服從零均值高斯分布的隨機值；若Fi,k≠0,Gi,k=0，則傳感器干擾或偏差模型為常見的時變系統；若Gi,k≠0，則該演化模型可描述傳感器偏差或干擾受到未知輸入的影響，比如突發的階躍信號輸入等。

說明3 參考文獻[12]中指出，可以通過對傳感器輸出信號進行變換使其干擾項變為零，即進行傳感器量測方程中的干擾或者偏差解耦，進而將量測方程受輸入干擾的濾波器設計轉化為傳統的無干擾量測系統濾波器求解問題。文獻[13-14]針對含有時不變的未知干擾輸入的系統設計了未知干擾解耦最優觀測器，文獻[15-16]針對一類不含隨機噪聲的具有未知干擾或輸入的線性系統設計了未知輸入觀測器。但是本文研究的未知干擾輸入是時變的，同時傳感器量測受到隨機噪聲的污染，因此文獻[12-16]中的相關算法并不適用于本文。此外，本文中傳感器受到的干擾或者偏差bi,k是無法避免的，因為這是進一步求解狀態估計的前提，不進行傳感器量測值的校準，將導致狀態估計發生嚴重偏差甚至發散。

本論文的目的是設計適用于狀態方程含未知干擾、量測方程含未知偏差影響下的動態隨機離散系統最小方差無偏估計濾波器。

2 雙重未知干擾解耦狀態估計器

本文針對狀態方程含未知干擾、量測方程含未知偏差的線性離散系統擬設計一種雙重未知干擾解耦下的最小方差無偏估計濾波器來估計多傳感器系統的狀態。最小方差無偏估計濾波器的設計主要包括兩步，第1步是設計傳感器量測偏差的最小方差無偏估計器：首先建立傳感器量測偏差系統模型，解耦線性離散系統方程中的未知干擾，然后設計最小方差無偏估計器，估計出量測偏差，進而校正動態系統測量值；第2步是設計未知干擾影響下線性離散系統的最優狀態觀測器：根據量測偏差校正系統測量值，然后對量測干擾偏差校正后的系統設計最優狀態觀測器，進而獲得具有最小方差無偏意義下的狀態估計，算法設計框架如圖1所示。

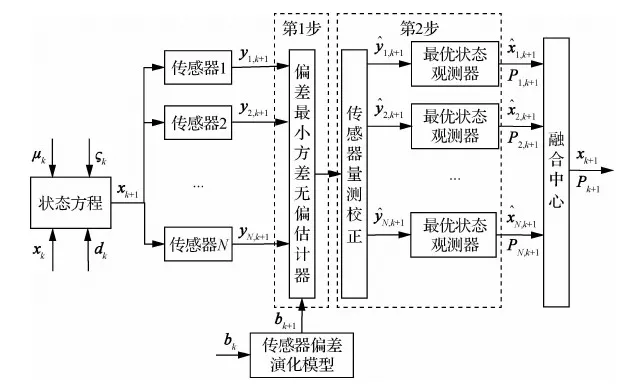
圖1 所提算法設計流程圖Fig.1 Flow chart of proposed algorithm

2.1 量測偏差最優估計器設計

2.1.1 量測偏差系統模型

將式(1)代入式(2)，得到k+1時刻第i個傳感器的量測方程為

yi,k+1=Ci,k+1xk+1+ηi,k+1+Di,k+1bi,k+1=

Ci,k+1(Akxk+Bkμk+ζk+Ekdk)+

ηi,k+1+Di,k+1bi,k+1

(4)

利用傳感器量測方程和傳感器偏差演變方程可以構造傳感器偏差系統模型，即對N個傳感器的量測進行線性組合，可得偏差系統模型為

q1y1,k+1)=(CN,k+1-qN-1CN-1,k+1-…-

q1C1,k+1)(Akxk+Bkμk+ζk+Ekdk)+

(ηN,k+1-qN-1ηN-1,k+1-…-q1η1,k+1)+

(DN,k+1bN,k+1-qN-1DN-1,k+1bN-1,k+1-…

-q1D1,k+1b1,k+1)

(5)

式中：qi∈R (i=1,2,…,N-1)為第i個傳感器的加權系數，并且0≤qi≤1。為了實現上述構造的偏差系統模型與目標狀態解耦，需要消除目標狀態信息，即式(5)中的第1項系數應為0，即

CN,k+1-qN-1CN-1,k+1-…-q1C1,k+1=0

(6)

此時，式(5)可寫為如下形式，定義為偏差系統模型的量測方程：

(DN,k+1bN,k+1-qN-1DN-1,k+1bN-1,k+1-…

-q1D1,k+1b1,k+1)=Hk+1bk+1+wk+1

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

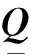
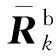
將式(3)中N個傳感器的系統偏差改為擴維的形式：

(15)

式中：

綜合式(7)與式(15)便構成了系統偏差模型。基于該模型，下面設計解耦濾波器進行系統偏差估計。

2.1.2 未知輸入解耦的量測偏差估計器設計

依據2.1.1節給出的偏差系統模型，本節給出一種基于最小方差無偏準則的量測偏差估計方法。該方法首先將量測偏差的未知輸入部分進行解耦，使偏差與未知輸入無關；隨后，基于解耦后的偏差系統模型設計一個最小方差無偏估計器。

(16)

式中:

證明：見附錄A。

定理2 基于式(7)與式(16)，可得最小方差無偏估計濾波器為

(17)

(18)

(19)

(20)

(21)

證明：見附錄B。

2.2 未知干擾解耦的最優狀態觀測器設計

傳感器偏差校正后的動態系統模型為

(22)

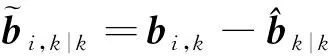
(23)

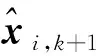
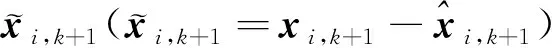
(24)

(25)

(26)

(27)

(28)

Mi,k+1=Ek(Ci,k+1Ek)?

(29)

Ti,k+1=I-Mi,k+1Ci,k+1

(30)

證明：見附錄C。

(31)

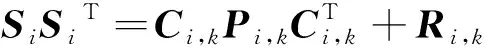
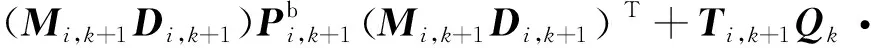
(32)

證明：見附錄D。

基于簡單凸組合融合算法實現N個傳感器的狀態融合：

(33)

2.3 所提方法實現步驟

基于2.1節和2.2節的推導和證明，針對多傳感器線性離散系統，本文所提的雙重未知干擾解耦的最小方差無偏估計濾波器的計算步驟如表1所示。

表1 雙重未知干擾解耦下的狀態估計濾波器

Table 1 Minimum variance and unbiased estimate filter with dual-decoupling unknown interference

%未知輸入解耦下的量測偏差最小方差無偏估計器1.按照式(8)～式(14)計算Hk+1、Q-、B-、bk、wk+1、Λ、Rbk得到偏差系統模型的量測式(7)。2.按照式(15)計算Fbk、Gbk、uk、bk、νbk、Qbk,得到偏差系統模型的狀態方程。3.按照式(16)計算Gbk+1、Fbk+1、Γbk+1。4.按照式(17)～式(21)分別計算^bk+1|k、Pbk+1|k、Κbk+1、^bk+1|k+1、Pbk+1|k+1。%未知干擾解耦下的系統狀態最小方差無偏估計器5.按照式(24)～式(30)分別計算Δ1i,k+1、Δ2i,k+1、Δi,k+1、A1i,k+1、Li,k+1、Mi,k+1、Ti,k+1。8.按照式(23)計算^xi,k+1、zi,k+1。9.按照式(32)計算Pi,k+1。10.按照式(33)進行狀態和協方差估計xk+1、Pxk+1。11.設置k=k+1,轉步驟1。

3 實驗仿真部分

飛行器徑向飛行控制系統簡化后的線性離散時間系統模型[12]為

xk+1=Akxk+Bkμk+ζk+Ekdk

Ekdk=ΔAkxk+ΔBkμk=

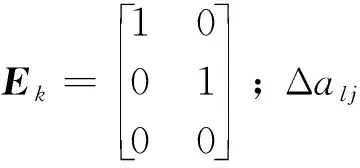
本文分別采用兩組加速度計和垂直陀螺儀來測量飛行速度、俯角和俯角率，系統量測方程為

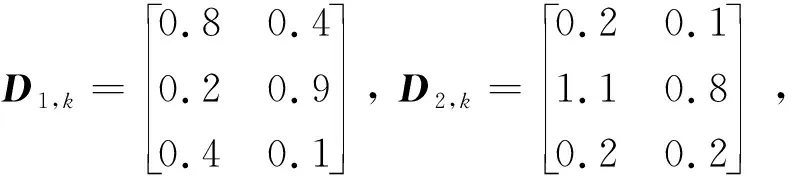
3.1 量測偏差估計結果及分析

本節對所提出的未知輸入解耦的量測偏差最小方差無偏估計器的有效性進行驗證。圖2和圖3 給出了與廣義最小二乘(Generalized Least Square, GLS)[17]和卡爾曼濾波(Kalman Filter, KF)[18]兩個方法的量測偏差估計結果對比。從圖2和圖3可以看出本文所提方法(Decoupled method)由于對傳感器偏差的未知輸入進行了解耦設計，進而基于傳感器偏差動態演化模型可以很好地跟蹤上兩個傳感器各個維度上的動態偏差值，這反映了本文提出的量測偏差最小方差無偏估計器的有效性。同樣基于動態模型估計的KF方法由于忽略了偏差動態演化模型中的未知輸入部分，而導致估計效果不佳。基于量測信息估計的GLS方法，不需要利用偏差動態演化模型，僅利用包含了系統偏差未知輸入的全部測量信息，因此估計效果基本可以接受，但相比本文所提的Decoupled method仍有較大差距。

為了更清晰地對比3種方法的估計性能，圖4 和圖5給出了100次蒙特卡羅仿真下兩個傳感器各個維度上的量測偏差估計RMSEs。可以看出本文所提Decoupled method在兩個傳感器各個維度上的量測偏差估計RMSEs最小，而KF方法和GLS方法在偏差由于未知輸入而發生突變時估計結果有較大波動。同時表2給出了不同算法偏差估計性能比較，可以看出本文所提的Decoupled method的平均RMSEs，相比基于量測信息估計的GLS方法至少提升了6.5%的性能，相比基于模型估計的KF方法至少提升了17%的性能，這驗證了本文所提Decoupled method方法在處理帶有未知輸入干擾下的傳感器偏差估計問題上明顯的優越性。從運算時間上可以看出，本文所提的Decoupled method相比其他兩個方法計算復雜度僅有略微的增加，這是可以接受的。

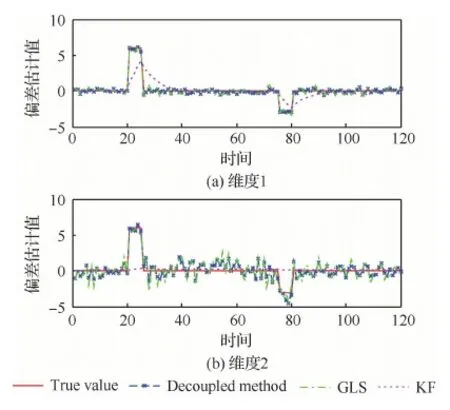
圖2 傳感器1量測偏差估計方法對比Fig.2 Comparison of bias estimate methods in Sensor 1

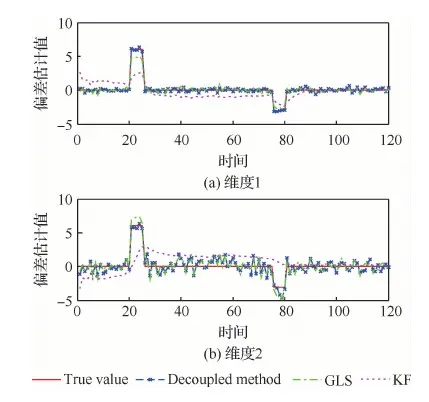
圖3 傳感器2量測偏差估計方法對比Fig.3 Comparison of bias estimate method in Sensor 2

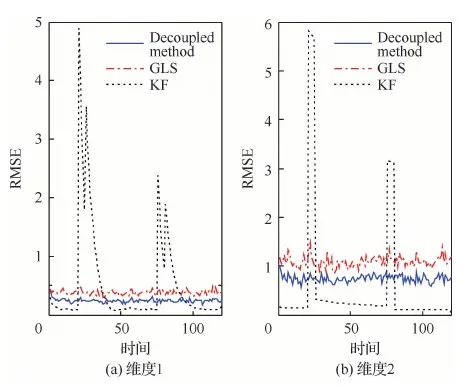
圖4 傳感器1量測偏差估計RMSEs對比Fig.4 Comparison of bias estimate RMSEs in Sensor 1

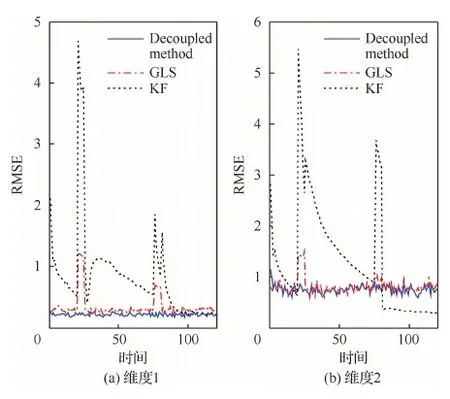
圖5 傳感器2量測偏差估計的RMSEs對比Fig.5 Comparison of bias estimate RMSEs in Sensor 2

表2 不同方法量測偏差估計性能比較Table 2 Comparison of performance of bias estimate

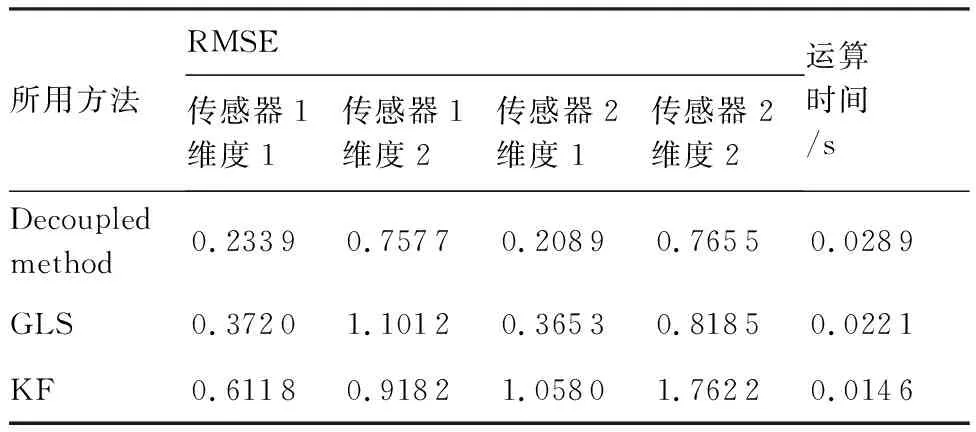
所用方法RMSE傳感器1維度1傳感器1維度2傳感器2維度1傳感器2維度2運算時間/sDecoupledmethod0.23390.75770.20890.76550.0289GLS0.37201.10120.36530.81850.0221KF0.61180.91821.05801.76220.0146

3.2 系統狀態估計結果及分析

本節對所提出的未知干擾解耦下的系統狀態最小方差無偏估計器的有效性進行驗證，并與未進行干擾解耦的聯邦卡爾曼濾波器[19](Federated Kalman Filter, FKF)和未進行傳感器偏差校正的方法(Decoupled method without Bias Compensation, DMBC)進行對比。圖6為不同方法在單次仿真下多傳感器狀態估計結果對比圖。可以看出DMBC方法由于未進行傳感器偏差補償，導致在傳感器偏差發生突變時不能正確地進行狀態估計，而FKF方法由于未考慮狀態演化模型中的未知輸入部分，導致整體估計效果不佳。而本文所提的Decoupled method不僅對狀態演化模型中的未知輸入進行解耦設計，同時對傳感器偏差進行補償，因此本文提出的最小方差無偏估計器估計結果更貼近真實的系統狀態，這進一步驗證了本文提出方法的有效性。

為了更清晰地對比3種方法的估計性能，圖7 給出了不同方法在100次蒙特卡羅仿真下狀態估計RMSEs結果對比。表3給出了不同方法狀態估計平均RMSEs以及運算時間的統計結果。可以看出，本文所提的Decoupled method方法在動態系統狀態3個分量(俯仰角，俯仰角速度，速度)的RMSEs都明顯優于其他2種方法。本文所提Decoupled method方法相比DMBC方法至少提升了17%的估計性能，相比FKF方法至少提升了65%的估計性能，這進一步反映了本文所提的未知干擾解耦下的系統狀態最小方差無偏估計器的優越性。同時值得說明的是，本文所提Decoupled method方法的運算時間是最長的，是以犧牲計算量為代價來換取估計性能的提升。

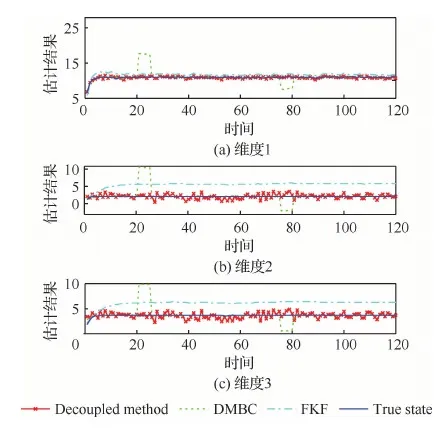
圖6 有/無偏差補償下狀態估計結果Fig.6 State estimate results with and without bias compensation

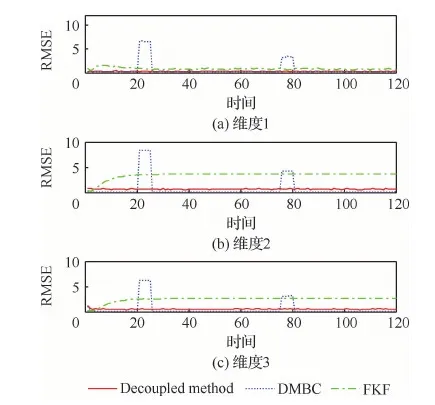
圖7 有/無偏差補償下狀態估計RMSEsFig.7 State estimate RMSEs with and without Bias compensation

表3 不同方法狀態估計性能比較

Table 3 Comparison of performance of state estimate using different method

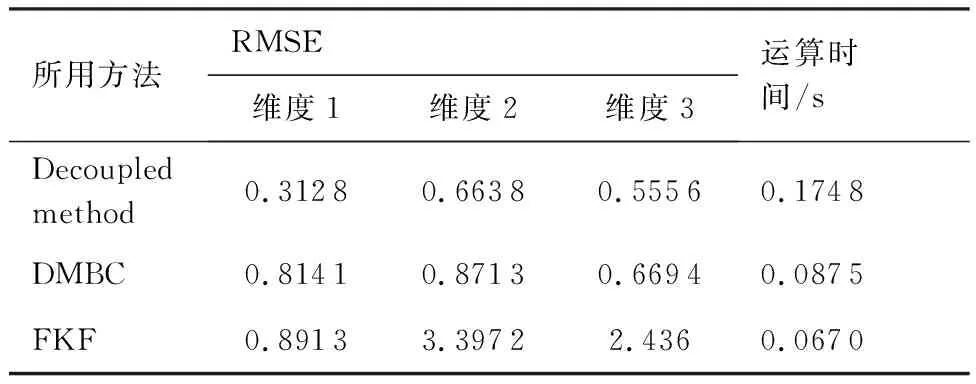
所用方法RMSE維度1維度2維度3運算時間/sDecoupled method0.31280.66380.55560.1748DMBC0.81410.87130.66940.0875FKF0.89133.39722.4360.0670

4 結 論

本文針對狀態方程含有未知干擾、量測方程含有未知偏差情況下的多傳感器狀態估計問題開展了研究，得到如下結論:

1) 基于量測偏差通用演化模型實現了偏差演化模型中的未知輸入解耦，進而設計了最小方差無偏估計器對量測干擾偏差進行估計。

2) 利用估計出的量測偏差進行動態系統測量值校正，根據量測干擾偏差校正后的系統模型設計了最優狀態觀測器，獲得了具有最小方差無偏準則下的狀態估計。

附錄A

將式(15)左右同時乘以傳感器偏差模型量測矩陣Hk+1，可得

(A1)

由式(7)可知

(A2)

聯立式(A1)和式(A2)，可得

(A3)

由式(A3)可得出uk的通解為

(A4)

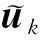
將式(A4)代入式(15)，可得

(A5)

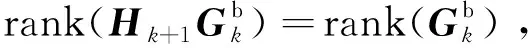
(A6)

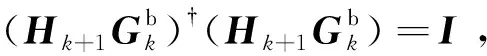
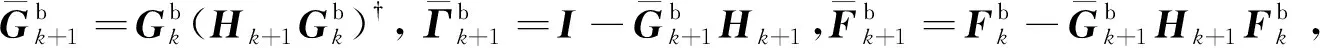
(A7)

證畢。

附錄B

(B1)

(B2)

(B3)

(B4)

因此，

(B5)

將式(B5)代入式(B1)～式(B4)中進行化簡，可得

(B6)

證畢。

附錄C

將最優狀態觀測器應用于具有未知干擾的隨機系統，即將式(23)代入式(22)中，狀態估計誤差為

xk+1-(zi,k+1+Mi,k+1(Ci,k+1xk+1+ηi,k+1+

(I-Mi,k+1Ci,k+1)(Akxk+Bkμk+ζk+Ekdk)-

Mi,k+1Ci,k+1)ζk-[Li,k+1-(I-Mi,k+1Ci,k+1)·

(I-Mi,k+1Ci,k+1)Ekdk-[Ti,k+1-

(I-Mi,k+1Ci,k+1)]Bkμk

(C1)

當rank(Ci,k+1Ek)=rank(Ek)成立時，Ci,k+1Ek為一列滿秩矩陣(因為矩陣Ek作為未知干擾輸入矩陣，默認為列滿秩矩陣)，則Ci,k+1Ek存在左逆矩陣，即

(Ci,k+1Ek)?=[(Ci,k+1Ek)TCi,k+1Ek]-1(Ci,k+1Ek)T

定義Mi,k+1=Ek(Ci,k+1Ek)+，則有

Mi,k+1Ci,k+1Ek=Ek(Ci,k+1Ek)+Ci,k+1Ek=

Ek[(Ci,k+1Ek)TCi,k+1Ek]-1(Ci,k+1Ek)T·

Ci,k+1Ek=Ek

即公式Ek=Mi,k+1Ci,k+1Ek恒成立。

再定義

(C2)

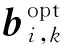
證畢。

附錄D

由式(C2)，可得狀態估計協方差矩陣為

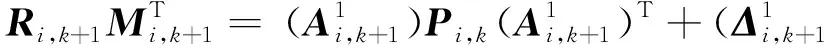
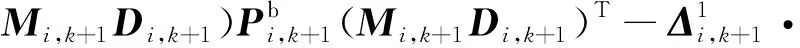
(D1)

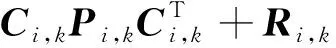
(D2)

令

(D3)

則協方差矩陣為

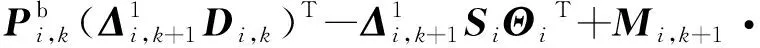
由式(D2)與式(D3)可得

(D4)

此時，狀態估計協方差矩陣由式(D5)給出

(D5)

證畢。