Matlab優化刀具在數控機床刀盤上的分布
蘇 展
(沈陽機床集團,遼寧 沈陽110000)
1 工程問題描述
數控立式車床較多采用“斗笠式”刀庫用以存放刀夾,如圖1。

圖1 “斗笠式”刀庫
某客戶定制的車銑機床,16種刀夾(如圖2所示)在重量上差別很大,其中的輕型銑刀重10 kg,而銑削角度頭為146 kg。若設計刀庫轉盤時刀夾隨機擺放,則刀庫整體重心就會根據刀夾的隨機分布而產生差異,極端情況下重心偏移刀庫旋轉軸心最遠,其旋轉的慣量也會增大,這樣會影響刀庫的使用壽命及旋轉定位精度。因此,設計出合力分布的車銑機床刀盤十分重要。

圖2 刀庫樣式及刀具種類
本文著重討論將16個刀夾合理分布在刀盤上的算法。
2 優化車銑床刀具分布
2.1 經典重心分布理論[1]
已知三維空間內,物體m1的三維重心在(x1,y1,z1);物體 m2的三維重心在(x2,y2,z2);............物體 mn的三維重心在(xn,yn,zn),整個系統的重心的位置在

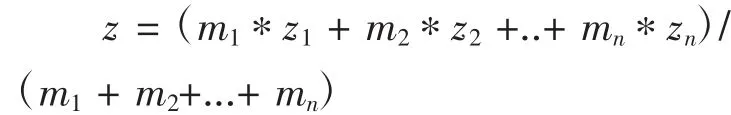
假設轉盤的重心位置與每把刀夾的重心在一個水平面上,則可以將此公式簡化至平面中計算。由于轉盤為旋轉體,其理論重心應在圓心上,將此點作為原點,而刀夾是均勻的分布在轉盤上的的分度圓(空位可以視刀夾的重量為0),所以建立極坐標更合適。應用Matlab編程結果如圖3所示。

圖3 轉盤體及刀具種類
2.2 Matlab優化轉盤重心
以現有一數控立式車銑床16工位刀庫為例:8個銑削刀夾10 kg;1個車削刀夾15 kg;2個車削刀夾45 kg;2個車削刀夾50 kg;2個車削刀夾75 kg;1個銑削角度頭146 kg。按照排列組合的思想,在不考慮重量的情況下,16把刀放在16個位置,共有16!=2.09e13個結果。將這些結果的每一組數值(即重量)分別與對應刀夾的坐標相乘,利用2.1節求解系統的重心公式,計算出各組排列重心,重心坐標距離圓心最小即為優化值。從而質量分布問題轉變為數值矩陣問題[2]。
Matlab的排列組合函數perms(n)的n建議不要超過8個[3],所以要利用這個函數必須人工降次。思路是:將這16個數按升序排列,再平均分成2組(前8個一組,后8個一組),先將前一組質量小的數進行數值運算,將優化的第一組結果保留,在此基礎上加入后一組數值進行第二次優化,最終得到最優解。此種方法同樣適用于多數值點(n>20)的情況。以下是matlab程序流程圖4。

圖4 程序流程圖
部分核心原程序如下:
n0= [10 10 10 10 10 10 10 10 146 15 45 50 75 75 50 45]
n_sort=sor(t n0)
n_result=zeros(size(n_sort
L_n_sort=size(n_sort);
n1=zeros(1,L_n_sor(t 2)/2);
n2=zeros(1,L_n_sor(t 2)/2);
n_sort_Search=1;
%部分內容省略,以下為核心算法
G_cal=sum(n0);
L_cal=0:pi/L:2*pi;
L_cal(length(L_cal))=[];
y0_cal=cos(L_cal);
x0_cal=sin(L_cal);
y_cal=reshape(y0_cal,length(L_cal),1);
x_cal=reshape(x0_cal,length(L_cal),1);
My_cal=n_result*y_cal;
Mx_cal=n_result*x_cal;
Gx_cal=My_cal/G_cal;
Gy_cal=Mx_cal/G_cal;
Gxy_cal=Gx_cal+i*Gy_cal;
R_cal=abs(Gxy_cal)
%部分內容省略,以下為核心算法
while text_i<=L_n_sort (2) text(y0_cal(text_i),x0_cal(text_i),[num2str(n_result(text_i))])
text_i=text_i+1;
以下是返回的數據,見圖5:
a1_result=10 10 10 10 10 10 10 10%第一組優化結果
a2_result=146 15 50 75 75 50 45 45%在第一組的基礎上第二組優化結果
n_result=10 146 10 15 10 50 10 75 10 75 10 50 10 45 10 45

圖5 重心優化結果
再將分布結果布置到刀盤的三維模型中如圖6所示,用質量除以密度得到不同體積的長方體擺放在各工位中(長方體的密度為45#鋼)。這樣就解決了在刀盤設計時平面分布不同重量刀夾問題。

圖6 16個刀夾在刀盤上的最優結果
3 結束語
本文利用Matlab的程序,適當的加入人工算法,將繁瑣的重復性的計算歸結為求極值的問題;技術人員僅需輸入多工位刀夾重量,便可解出刀盤平面內刀夾分布的最優解。

