某核電海水循環泵齒輪箱振動分析

靳曉樂

（中廣核工程有限公司調試中心，廣東 深圳518124）

0 引言

齒輪嚙合產生的振動頻譜中的主要頻率成分包含齒輪軸轉頻、齒輪嚙合頻率及其倍頻，這些嚙合頻率周圍的頻率分布稱為邊頻帶。由于齒輪運行時有多個激勵源，在齒輪嚙合頻率及其諧波或齒輪固有頻率及其諧波周圍會出現邊頻帶。一般情況下，當齒輪箱發生某些故障時，故障的特征頻率及其諧波會對齒輪箱的振動信號產生調制，在頻譜圖上齒輪箱嚙合頻率及其諧波兩側會有一系列邊頻帶，這些邊頻帶中包含豐富的齒輪狀態信息，通常作為齒輪故障診斷的重要依據。

齒輪故障診斷技術最早起源于美國，它是現代工業基礎上出現的一門新興科學。齒輪故障的診斷方法包括兩類：一種是通過處理分析齒輪運行時的動態信號來進行齒輪故障診斷；另一種是以摩擦磨損理論為依據，對齒輪箱潤滑油中的磨屑進行研究分析，從而判斷齒輪的運行狀態。國外的齒輪狀態監測與故障診斷技術發展已經趨于成熟，并領先國內該技術的發展。美國主要側重于對齒輪箱狀態監測和故障診斷的軍事方面的研究，而日本則側重于一些民用工業。齒輪的故障或失效形式多樣，這就使得對它進行故障診斷難度較大，而目前國內外已有的故障診斷系統還不完善，大多應用于定性分析，存在一定的局限性。

某核電采用立式行星齒輪箱作為海水循環泵減速機構，每臺機組配備4臺海水循環泵，每臺泵均配置一臺行星齒輪箱作為減速機。第1臺齒輪箱首次滿載啟動時，使用便攜式測振設備測量行星齒輪箱軸向振動超過限值，垂直方向達到6.1 mm/s。針對該齒輪箱振動偏高問題，對振動信號進行了采樣。測量得到該齒輪箱振動幅值低于驗收標準，由于齒輪組嚙合的復雜性，為進一步判斷是否存在局部故障，基于邊頻帶理論對其頻譜圖進行了分析，分析結果表明該齒輪箱不存在局部故障，其振動烈度符合相關標準，滿足長期穩定運行的要求。

1 齒輪箱參數及振動標準

齒輪箱的參數如下：

類型：行星齒輪/外齒圈固定

齒數：太陽輪26，行星輪51，內齒圈130

行星輪數量：4

轉速：995.6 rpm/165.9 rpm

根據齒輪箱參數計算得到齒輪箱各部件的轉速和頻率如表1。

表1 齒輪箱轉速和頻率

該齒輪箱由供應商依據ANSI/AGMA 6123-B06和ANSI/AGMA2001-D04進行設計，其振動標準有供應商依據AGMA2000及其設計經驗進行定義。齒輪箱的振動報警值為5.1 mm/s RMS[10-1000]Hz，停機值為7.9 mm/s RMS[10-1000]Hz。

2 數據采集

振動測量：

齒輪箱共安裝2個三軸加速度傳感器，見圖1，測點1為齒輪箱輸入端，測點2為齒輪箱輸出端。

圖1 加速度傳感器布置

齒輪箱滿載穩定運行狀態下的振動幅值見表2。測量得到齒輪箱振動幅值均低于限值，完全符合標準要求。

表2 振動測量值（單位mm/s）

3 振動分析

3.1 與振動標準進行比較

測量得到的齒輪箱振動數據均在標準限值以內，完全符合標準要求。但是，齒輪箱的振動相比首次啟動有較大差異，分析原因有以下兩點：

（1）首次滿載期間的測振點定位于齒輪箱殼體的最外側，該處距離軸承較遠，由于局部形變導致測量值較高；根據標準推薦，測點應該盡可能靠近軸承，本次測振點選取靠近軸承位置。

（2）首次滿載測量所用儀表為一體式便攜測振儀，測振探頭與本體為整體，易受使用者影響，導致測量值不準。本次測振采用強力膠將傳感器固定在測點表面，通過電纜連接到拾取器，消除了人為因素導致的測量偏差。

由于齒輪組嚙合過程十分復雜，振動強度不能完全準確的反應齒輪組的運行情況，因此需要對齒輪箱的振動信號進行分析，下面基于邊頻帶理論從不同角度對齒輪箱的振動信號進行分析。

3.2 基于邊頻帶理論的無故障頻譜特征分析

齒輪箱嚙合產生的頻譜中，主要頻率成分包含齒輪軸轉頻、齒輪嚙合頻率及其倍頻。嚙合頻率周圍的頻率分布稱為邊頻帶。

文獻[2]中提出了一種簡化的數學模型來描述無故障狀態下行星齒輪組邊頻帶的產生機理，并通過試驗驗證了該模型，該模型適用于普遍的行星齒輪結構。

本文分析的齒輪箱的結構如圖2所示，其行星輪數量為4，行星齒輪等間距分布。

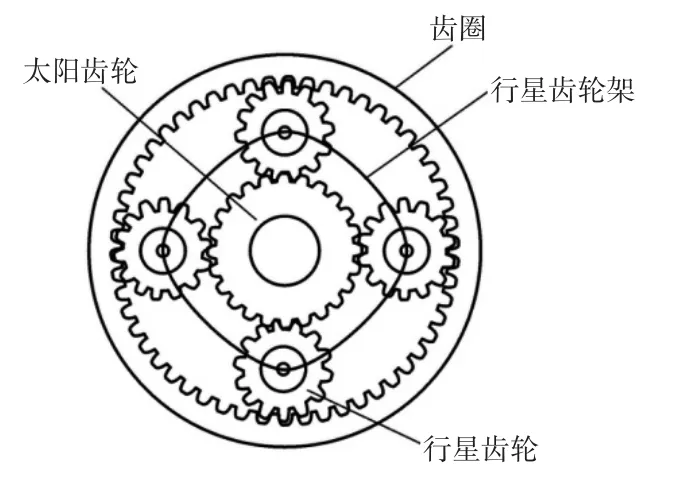
圖2 齒輪箱結構示意圖

針對行星輪數量為4的等間距行星齒輪結構，其振動頻譜及邊頻帶的理論模型如圖3所示[2]。

圖3 等間距行星齒輪理論頻譜

泵組穩定運行狀態下齒輪箱的振動頻譜如圖4所示。其主要能量集中在360 Hz和720 Hz附近，由嚙合頻率及其二次諧波引起的。因此僅需對360 Hz和720 Hz附近區域進行分析。

圖4 頻譜圖

將Z方向300～400 Hz，670～770 Hz的區間放 大，得到細化譜圖5。

圖5 細化譜

細化譜中并未出現理論嚙合頻率，僅能看到嚙合頻率的二次諧波。其頻譜特征符合該類行星齒輪箱結構的理論頻譜模型（見圖3）。在圖5中可以看到嚙合頻率和二次諧波兩側有少量邊頻帶，間隔分別為5.5 Hz和11 Hz，但其幅值并不大。11 Hz的邊頻帶反應了行星齒輪的通過頻率，5.5 Hz則與齒輪箱低速側的二次諧波頻率相吻合。因此這些邊頻帶反應了行星通過頻率和低速側轉軸頻率對齒輪箱振動頻率和幅值的調制。

以上現象完全符合圖3的理論振動頻譜模型，因此該齒輪箱的頻譜特征符合典型的無故障等間距行星齒輪組特征。

3.3 基于邊頻帶理論的局部故障特征分析

文獻[3]提出了行星齒輪箱局部故障特征頻率的通用公式：

太陽輪局部故障特征頻率為

行星輪局部故障特征頻率為

外齒圈局部故障特征頻率為

其中fm為嚙合頻率，ZS為太陽輪齒數，Zp為行星輪齒數，Zr外齒圈齒數，N為行星輪數量。

計算得到本文齒輪箱局部故障特征頻率見表3。

表3 齒輪箱故障特征頻率

太陽輪故障邊頻帶的峰值將出現在

行星輪故障則邊頻帶的峰值將出現在

外齒圈故障則邊頻帶的峰值將出現在

fc為行星架旋轉頻率，k為正整數，n為整數。

圖 5 中 的 峰值頻率 342.9 Hz，353.9 Hz，365.2 Hz，376.1 Hz均不符合以上三個算式，所以可以排除齒輪存在局部故障的可能。

4 結束語

該齒輪箱首次滿載期間，由于測振點選取不當及測振儀器易受使用者影響，造成測得的振動強度超出驗收標準，首次測振數據并不能真實反映齒輪箱的運行狀態。本次測振在消除以上兩個因素的前提下，測得的頻譜圖表明，其振動強度均在標準限值以下；對齒輪箱進行基于邊頻帶理論的分析表明，該齒輪箱的運行狀態良好，其振動頻譜符合無故障齒輪組的典型特征；通過對本齒輪箱局部故障特征頻率的對比，可以排除齒輪組局部故障的可能。綜上，該齒輪箱運行狀態良好，振動強度在標準限值以下，滿足長期穩定運行的要求。