共焦雙曲柱面電極的電場及其數值模擬

王 福 謙

(西南交通大學 希望學院 基礎部，成都610400)

0 引 言

由復變函數理論可知，解析函數的實部和虛部分別滿足拉普拉斯方程，且其實部為常數和虛部為常數的兩族曲線互相正交。在靜電場中，解析函數的這一特性使其代表一定的平行平面場，其實部和虛部分別代表勢函數(或通量函數)和通量函數(或勢函數)。不同的解析函數的實部和虛部可描繪出不同的幾何圖形，如果某一解析函數所給出的幾何圖形與所討論問題的邊界的等勢線或等通量函數線相吻合，則此解析函數的實部或虛部可作為待求勢函數(或通量函數)和通量函數(或勢函數)的解，即用此解析函數作為所求靜電場的復勢來求解電場分布。

復勢函數法為求解復雜二維邊值問題的一種有效方法[1-2]。文獻[3-10]中利用復勢函數法討論了非平行板電容器電場、扇形導體中的電場、線電荷與無限大接地導體板間的電場及共焦橢圓柱電纜的磁場等復雜形狀邊界的靜電場和靜磁場的邊值問題，但用該方法對復雜形狀電極的電場分布的研究，相關文獻還未見報道。本文利用復勢函數法研究雙曲柱面電極的電場，給出其電勢分布、場強分布函數及電極頂點處的場強，討論電極形狀蛻變的幾種特殊情形，并通過Matlab數據處理軟件的數值計算功能進行數值模擬，繪制出其電場線和等勢線圖。

1 電勢函數與通量函數

有一對共焦雙曲柱面的電極，其實半軸和虛半軸分別為a1、a2和b1、b2，左側電極接地，右側電極的電勢為U，其橫截面如圖1所示。因在垂直于雙曲柱面母線的所有截面上的電場分布均相同，故本文所研究的電場為平行平面場。由于本文所討論的二維邊值問題的電勢函數滿足二維拉普拉斯方程，且其邊界與反余弦函數實部所表示的曲線族中的曲線重合，故可選用反余弦函數作為所求靜電場的復勢[11]，即

W=Aarccos(z/k)+B

(1)

可進一步表述為

W=Aw+B=A(u+iv)+B1+B2

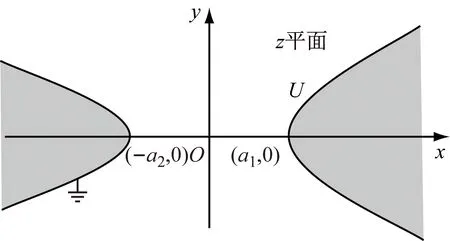
圖1 共焦雙曲柱面電極的橫截面

令式(1)中的電勢函數和通量函數分別為φ和Ψ，則

φ=Au+B1

(2)

Ψ=Av+B2

(3)

對圖1右側的雙曲線頂點處(a1,0)，式(1)有：

U=Aarccos(a1/k)+B1

(4)

對圖1左側的雙曲線頂點處(-a2,0)，式(1)有：

0=Aarccos(-a2/k)+B1

(5)

再者，由于式(3)中的附加常數可取任意值，故令

B2=0

(6)

由式(4)～(6)，可得：

故共焦雙曲柱面電極電場的復電勢為

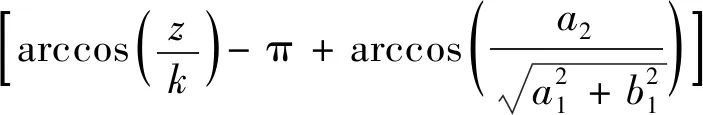
(9)

共焦雙曲柱面電極電場的電勢函數和通量函數可分別表示為:

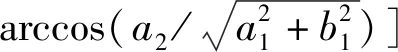
(10)

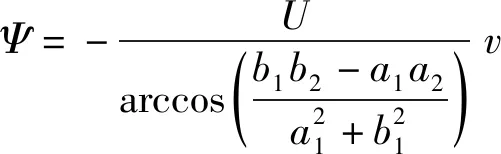
(11)

式(1)中的反余弦函數亦可表述為[12]:

iln{x+F1cosα+i[y+F1sinα]}-ilnk=

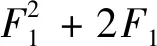
(12)

式中:

由式(12)得:

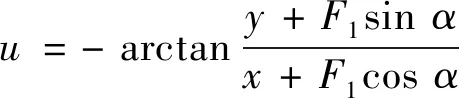
(13)

2F1(xcosα+ysinα)]-lnk

(14)

將式(13)、(14)分別代入 式(10)、(11)，可得共焦雙曲柱面電極電場的電勢函數和通量函數分別為:

(15)

2F1(xcosα+ysinα)]-lnk

(16)

2 場分布數值模擬及電極形狀蛻變特殊情形

2.1 場分布的數值模擬

為了給出共焦雙曲柱面電極電場分布圖的直觀圖像，以驗證本文所得結論的正確性,下面用Matlab對該電場分布進行數值模擬[13-15]，其電場線和等勢線的分布見圖2(取U=150 V)。由圖2可見,圖中的電場線與等勢線及導體邊界均垂直，場線分布正確，為預期結果。

2.2 電極形狀蛻變的特殊情形

當共焦雙曲柱面電極的實半軸和虛半軸取一些特殊值時，可得到幾種特殊情形下的電場分布:

(1)雙曲柱面電極的實、虛半軸的長度分別為5、0和4、3時，右雙曲柱面電極蛻變為帶電板，此情形的電場為水平帶電平板與雙曲柱面電極所形成(見圖3)。

(3)左雙曲柱面電極的實半軸和虛半軸的長度分別為0.01、5和5、0.01時，兩雙曲柱面電極蛻變為相互垂直的帶電板，此情形的電場為雙相互垂直的帶電板所形成(見圖5)。

(4)左、右雙曲柱面電極的實半軸和虛半軸的長度均為5和0.01時，左、右兩雙曲柱面蛻變為共面平板，此情形的電場為共面帶電平板為所形成(見圖6)。

(5)左、右雙曲柱面電極的實半軸和虛半軸的長度均為6和無限大時，左、右兩雙曲柱面蛻變為平行板，此情形的電場為大平行帶電板所形成(見圖7)。

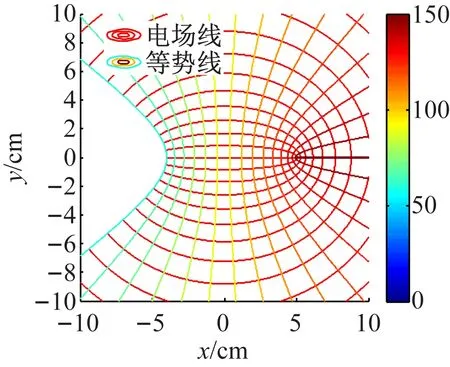
圖3 帶電板與雙曲柱面的電極的電場

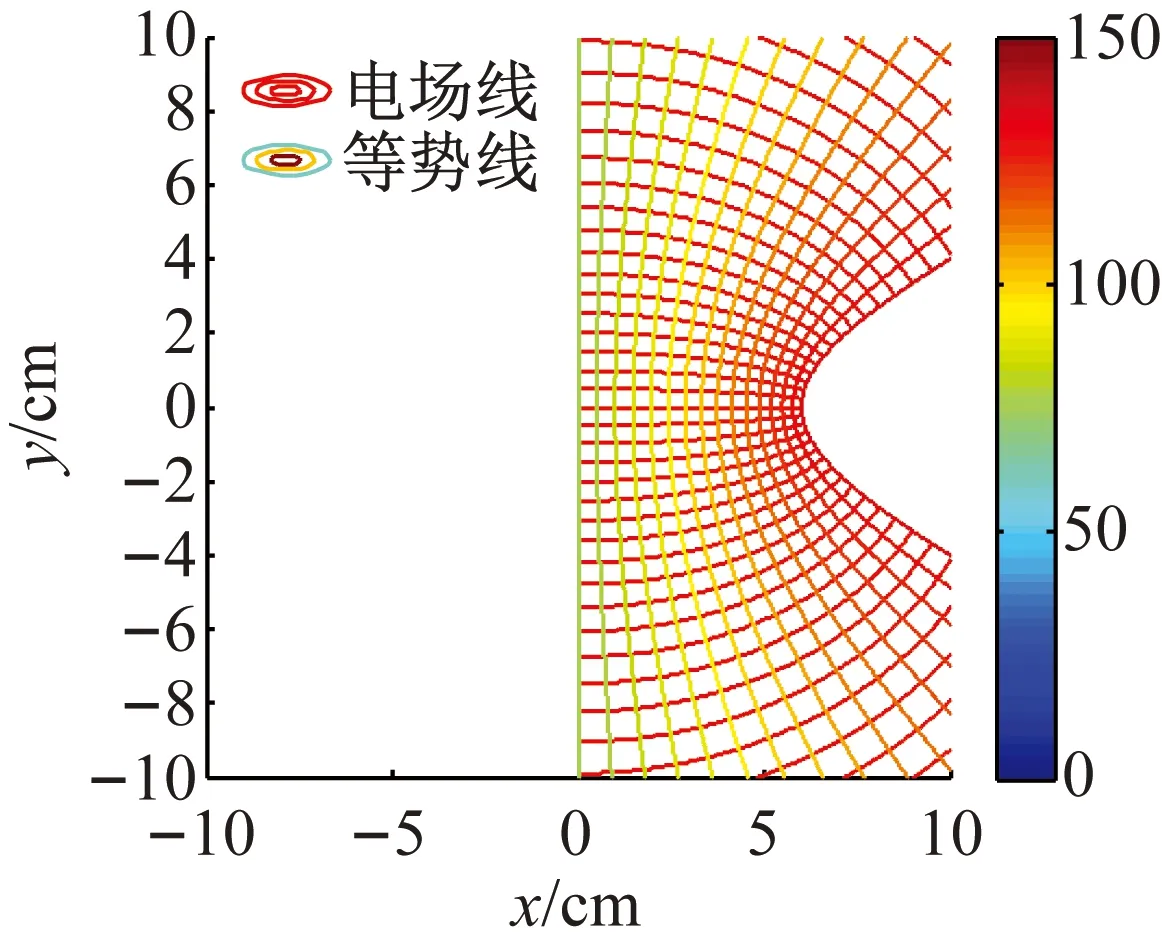
圖4 雙曲柱面的電極與帶電板的電場

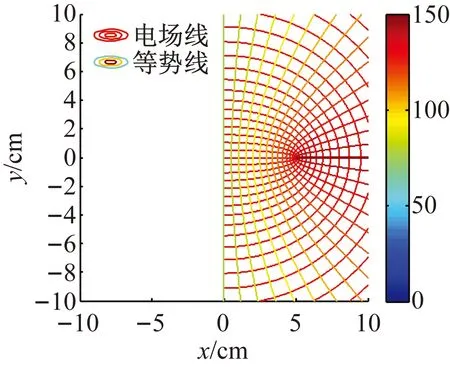
圖5 兩垂直不相連的帶電板間的電場

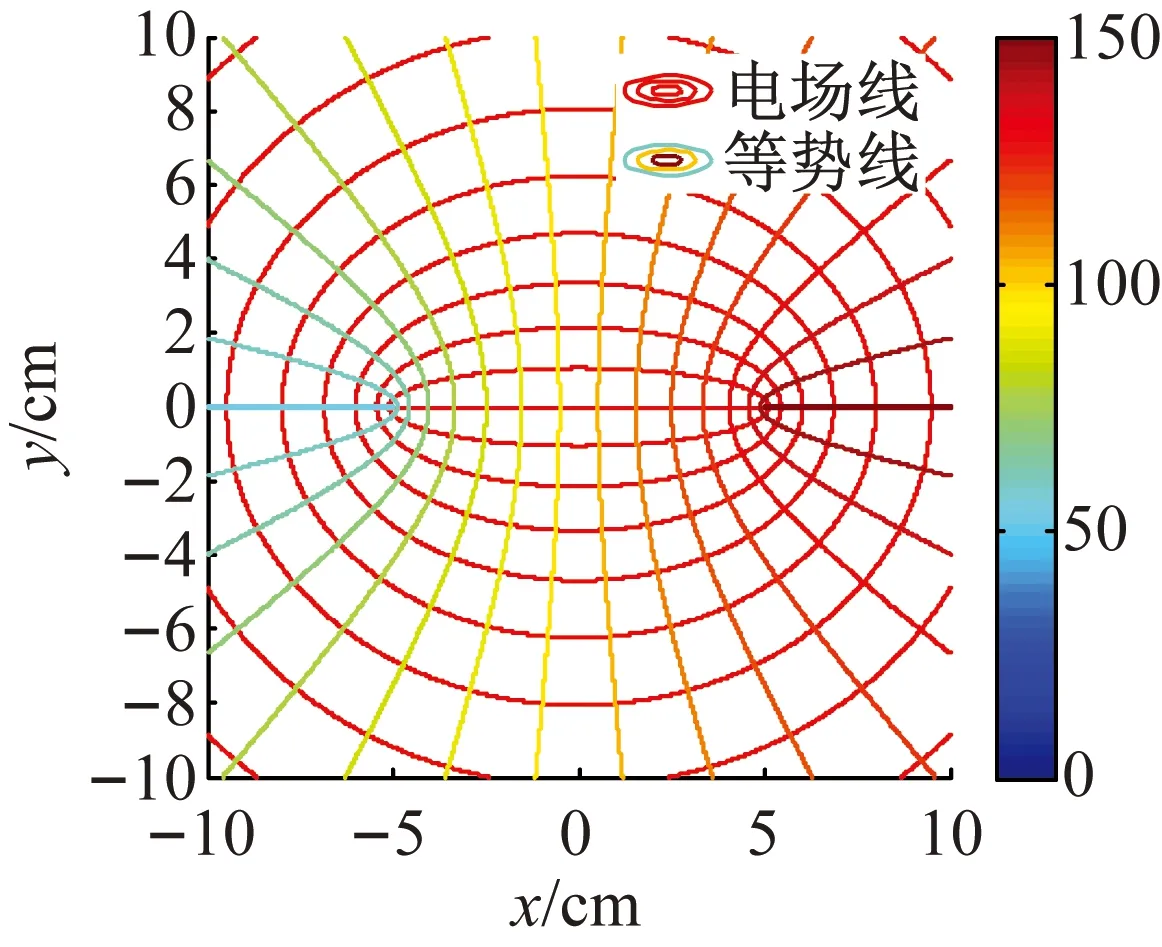
圖6 兩共面不相連的帶電板間的電場

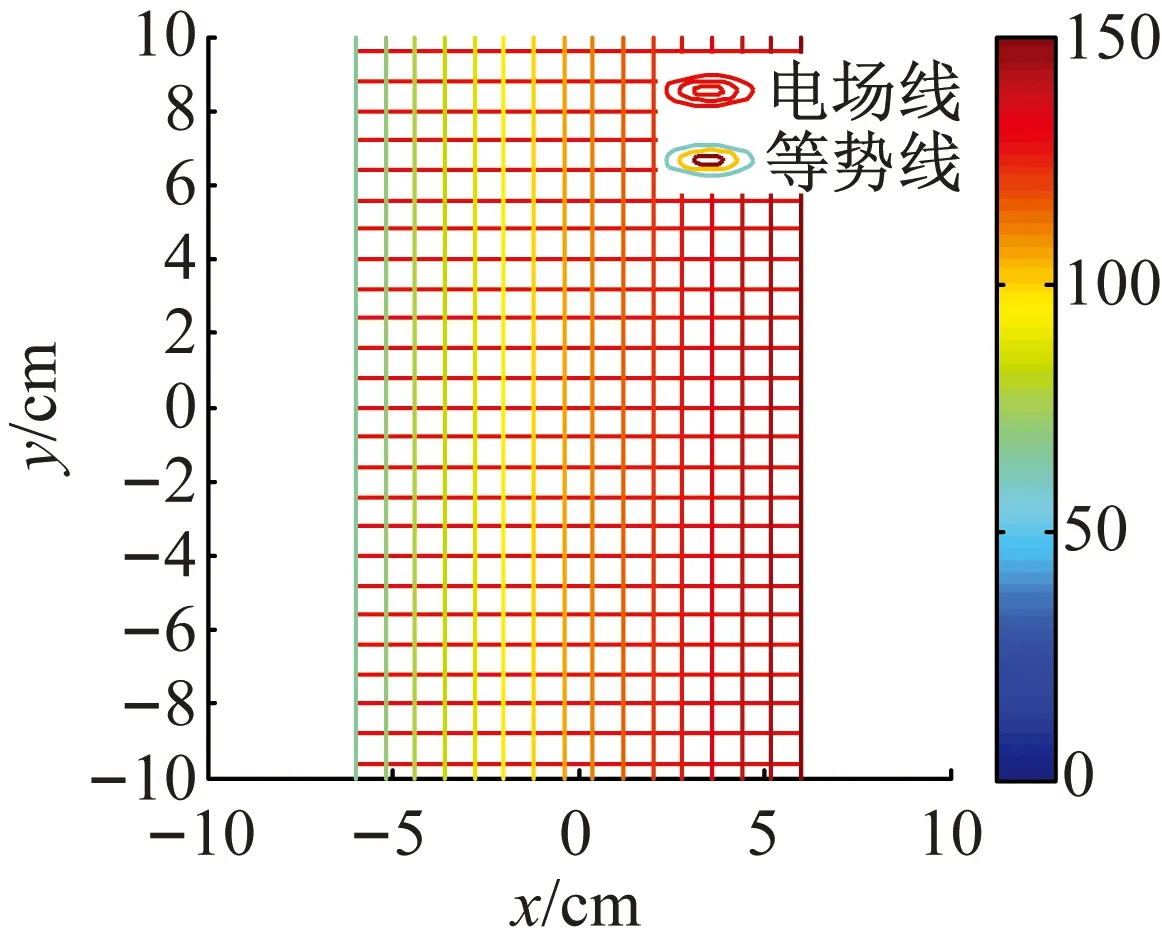
圖7 平行帶電板間的電場

所以，雙曲柱面電極和帶電平板所形成的電場、兩相互垂直不相連的帶電板所形成的電場、共面帶電平板所形成的電場及平行帶電板所形成的電場，均為本文所討論問題的特例,本文的研究結論具有一定的普遍性。

3 電極場強分布及電極頂點處場強

由式(9)，根據電場強度與復勢函數關系E=-[dW/dz]*，可得共焦雙曲柱面電極電場的電場強度的復數形式為

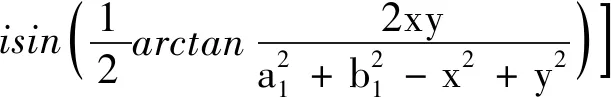
(17)

對于雙曲柱面電極的兩頂點處，其坐標分別為(a1,0)和(-a2,0)，將此兩坐標值分別代入上式，則得雙曲柱面電極的頂點處的場強大小分別為:

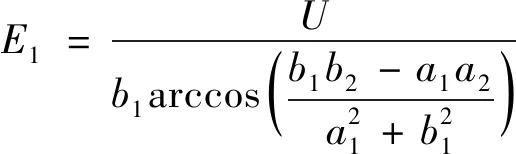
(18)

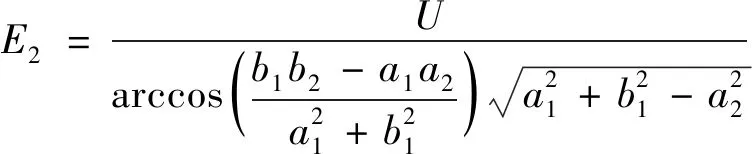
(19)

由表1可以看出：當雙曲柱面電極頂點處曲率變大時，其附近的場強增大，而當雙曲柱面電極的形狀蛻變為兩共面帶電板時，其端頭間的場強最強；當雙曲柱面電極頂點處曲率變小時，其附近的場強減小，而雙曲柱面電極的形狀蛻變為兩平行帶電板時，其間的場強最小，且為勻強電場。

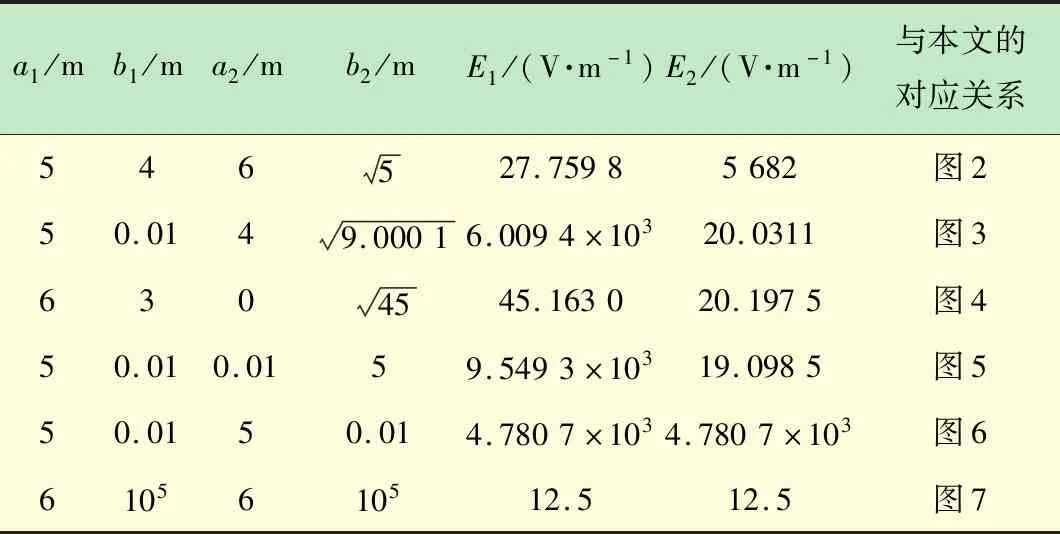
表1 雙曲柱面電極頂點處的場強

4 結 語

本文將理論計算與數值模擬相結合，利用復勢函數法研究研究雙曲柱面電極的電場，得到了其電勢分布和場強分布函數，并利用Matlab軟件對場分布進行了數值模擬，給出了場分布的直觀圖像，為邊界形狀復雜的電極的電場分布問題的求解提供了一種新的方法，在科研上具有一定的理論意義和實用價值。