數學教學中 “兒童思維可視化”探析

吳麗麗

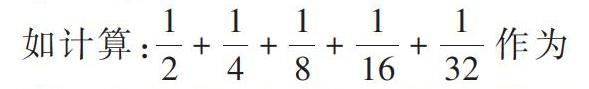
數學，一般以靜態的素材呈現方式和抽象的邏輯思維訓練出現在兒童的視界中，在兒童的視野中數學未免有些冰冷，有些乏味，有些不可觸摸。而兒童思維可視化可以運用一系列圖示技術把本來不可視的思維（思考方法和思考路徑）呈現出來，使其成為清晰可見的過程。被可視化的“思維”更有利于理解和記憶，因此可以有效提高信息加工及信息傳遞的效能。思維的可視化與教學的深度融合，能收獲學程的精彩，成就學生的精彩。

著名的特級教師許衛兵校長，在一次講座上分享了一個提分的金點子：“在每次考試的解題過程中，學生必須在草稿紙上清晰地記錄有關思考過程。”這個金點子的實質就是“思維可視化”。“可視化”讓孩子們的知識和思維過程都變得清晰、準確，減少了干擾因素，降低了思維跨度，幫助孩子實現自我認知監控和調節，減少錯誤的發生。當“思維的可視化”與教學激情相遇，又會成就怎樣的精彩？

一、“思維可視化”，改造學習的可為之術

離開“思維”的“知識”就變成“死知識”，必然是枯燥的、低效的、令人厭倦的，更重要的是“死學習”會使學生長期處于“淺思考”甚至“不思考”狀態，從而導致思維能力發展受阻。而思維能力又是學習能力的核心，因此，提高教學效能的關鍵并不在于“知識重復的次數”，而在于“挖掘與呈現知識背后的思維規律并讓學生掌握它”。因此“思維可視化”是學生在學習過程中得到有效發展的重要途徑，同時會使學生對知識的理解更深入、更透徹、更系統，從而進入會學、樂學的良性循環。

二、“思維可視化”，提高學習效能重要方法

在傳統教學模式中，“知識加工”和“問題解決”的思考過程往往是不可見的，而且教師和學生都更多地關注答案，忽視答案的生成過程。然而，學生思維的發展并不來自“答案的累積”，而來自“生成答案的思維方法和過程”。因此，我們必須要把“看不見”的思維過程和方法清晰地呈現出來，以便更好地理解、記憶和運用。

1.概念圖。概念圖重在對概念關系的呈現，用鏈條式連接，形成框架體系，將靜態的知識文本通過“可視化”方法呈現，以利于學生更清晰地理解知識要點，了解知識產生的過程以及知識間的相互聯系，更好地把握知識的重難點。

如在梳理“比和比例”這一部分內容時，先布置學生在對這部分知識理解和掌握的基礎上，整理和繪制這一內容的概念圖。教學時讓每組選派代表上臺講解，其他小組進行評價。這不僅能培養學生的語言表達能力和團隊合作精神，還能讓學生更加明確當前所學的概念在所學知識基礎上的發生、發展和延伸的情況，以進一步溝通概念之間的聯系，使學生在頭腦中形成系統化的教學認知結構。

2.思維導圖。數學思維導圖可以呈現學生每一步思維過程，讓所有思考的過程都可視化，既可以清晰地表達思維的每一步走向，又能夠快速有效的尋求到解決問題的最佳方法。

如在復習分數應用題時，很多學生拿到題目分不清是用除法還是乘法，因此，就要讓他們在課前通過小組合作的方式，把拿到分數應用題時自己分析思考的方法用思維導圖的方式表示出來。這樣學生對分數應用題的思路更清晰，知道解決分數應用題的關鍵是：判斷單位“1”的量是已知的還是未知的。真正實現數學知識的自然貫通與數學思維的多維生長。

3.線段圖。小學數學教學中經常要用直觀的線段圖等可視化手段表示抽象的數學語言，不僅實現抽象與具體的聯系，也有利于孩子形成正確地問題表征，清晰感知條件和問題間的操作空間，借助數量關系和分析方法，獲得問題解決。如在教學“行程問題”時，讓學生先根據題意畫線段圖，學生用幾種不同的線段圖表示。每種線段圖都是建立在學生自我理解建構的基礎上，學生在自我解述與建議中不斷地優化思維過程，教師只需做好組織者、引導者的角色，讓學生在自我反思中修正優化。這樣的思維可視使數量關系更清晰，學生理解更透徹。

三、“思維可視化”，有助于解題策略的分析

小學階段學生的思維正從形象思維向抽象思維發展，對圖示、符號等語言更加敏感，可借助思維可視化為跳板，順利地完成思維的進階發展及過渡。

（一）“符號和圖示”的外化使“思維可視化”

在數學教學中，要結合學生的年齡特征和認知規律，幫助兒童借助圖形和符號進行數學思考，并能將自己的思考過程記錄下來，是兒童最常用的思維可視化的解題策略。

如“排隊問題”：二（1）班小朋友做操排隊，小麗站在第一排，從左往右數小麗排在第5個，從右往左數小麗排在第二個，第一排一共有多少位小朋友？在解決這類題目時，我鼓勵學生用自己喜歡的方法把解決問題的過程記錄下來。? 學生有的用不同形狀的圖形表示出小麗從不同方向站位的情況，并能根據圖示列出算式，有的用類似“韋恩圖”的方式表示，突出重合的部分，有的用線段圖的方式表示。不同的圖示方法都可以幫助學生解題，還能清晰的呈現學生在解決問題時的思考過程。讓學生的思維對教師可見，對自己和同學可見。

（二）“教學難點”外化使“思維可視化”

小學數學不僅有高度概括的知識和原理，很多數學題目本身也是極具抽象性的。因此在講解過程中適當引導學生轉化思路，運用多角度的幾何圖式使解題思維可視化。

如計算：[12+14+18+116+132] 作為教師沒有直接告知學生“可以結合圖形進行思考”，揭示數與形之間的關系，而是讓學生在繁難的通分計算后，形成認知沖突，從而在教師的正確引導和學生的積極思考中，使學生思維過程可視化。讓學生在可視化的模型中進行知識建構，逐步分解新知。

“思維可視化”教學不僅可以改善知識的掌握，思維能力的開發。更給我們的教育教學增添了許多附加值。讓知識更清晰，聯系更緊密，內涵更豐富;讓思維更縝密，思路更開闊;讓互動更流暢，交流更有效;讓學習更自信、自主、自動。