空間站艙外泄漏羽流場數值模擬

花 雨，畢海林，孫 偉，孫立臣，孟冬輝，王旭迪*

（1. 合肥工業大學 機械工程學院，合肥 230041； 2. 北京衛星環境工程研究所，北京 100094）

0 引言

載人航天器在軌運行中受到各種外部因素的影響，若密封性遭到破壞，會使其內部壓力發生變化，危害航天員的生命安全。因此，有必要對艙內氣體外泄過程進行研究，找到快速定位漏孔，測量漏率，判斷風險的有效方法。

目前國內對于空間站外部漏孔快速定位的研究仍然處于初步階段，一般利用方向規[1]定位漏孔的位置并測量其漏率。國外，Woronowicz等[2-4]通過求解無碰撞的玻耳茲曼方程獲得了真空羽流的物理和數學模型，并采用直接模擬蒙特卡羅（DSMC）方法驗證了模型的可靠性，還研制出一種真空羽流的自動檢測實驗裝置：在真空腔室中設置一個可以旋轉和平移的平臺，將質譜儀和全壓計放置在平臺中心，通過平臺的旋轉和平移測試腔室不同位置的分壓，可實現漏孔的快速定位。Fuchs等[5]發現：以液氨作為示漏工質，當氨蒸氣由一定面積的小孔泄漏到超高真空環境形成羽流，可通過精確的動力學理論分析計算較好地預測羽流測量結果。新墨西哥州立大學的Cai等[6]利用DSMC方法，結合稀薄氣體動力學，給出無碰撞的圓孔、環孔噴射羽流的物理及數學模型，并將此模型應用于推進器羽流的數值模擬中，為泄漏氣體從高壓側向真空側高速運動的模型建立提供了理論依據。

本文參照Woronowicz等人的仿真思路，結合Cai等人的物理模型，在分析空間站泄漏處環境因素的基礎上，針對特定的環境參數設置了特定的泄漏邊界條件，并以DSMC方法為工具，分析得出了典型漏孔形狀和位置對泄漏處附近羽流場的影響，以期為后續實驗提供數據支持。

1 仿真對象分析

空間站軌道高度為350～400 km，處于大氣層的熱層，大氣成分主要為原子氧，且粒子數密度在1×1015/m3左右[7]；波長小于 0.175 μm 的太陽紫外輻射被熱層中的大氣物質所吸收，使氣溫隨高度的增加而迅速增高，空間站外的大氣溫度約為1000 K[7]。因此，設置模擬溫度為 1000K，泄漏處的粒子數密度為1×1020/m3[8]。由于漏孔內外壓差很大，所以將氣體從漏孔進入真空考慮為聲速擴張，聲速計算公式為

式中：k為傳熱系數；R為摩爾氣體常數；T為漏孔孔口處的熱力學溫度。則上述模擬條件下的聲速約為800 m/s。除此之外，還應考慮空間站不同位置處的外部結構以及漏孔的大小和形狀對羽流場的影響。

真空泄漏羽流場在不考慮外部干擾因素的情況下是對稱分布的，因此本文采用二維模擬。模擬設置的流場尺度為 0.5 m×0.3 m[3]，漏孔設置在流場左側中心的位置，泄漏處管道的壁厚為1 mm[4]。相關資料顯示[4]，當空間站的泄漏漏孔直徑達到mm量級時就會對空間站的正常運行產生較大的影響，因此本研究將漏孔直徑分別設置為1、2、3 mm。導致航天器泄漏的原因比較復雜，包括人為操作不當、部件老化或者微流星碰撞等，因此在考慮漏孔形狀時不能一概而論，本研究選取張口孔、縮口孔和平行斜孔3種典型漏孔形狀（如圖1所示）。空間站的外部結構極其復雜，遍布管道和桁架，還有各種不同功能的腔體暴露在空間站外部，因此漏孔所處的位置可能會在任何角落，本研究選取拐角、斜邊、夾角處等典型位置的漏孔（如圖2所示）。仿真分析時，以上參數設置只需在軟件中對幾何模型進行相應修改即可。

圖1 三種漏孔形狀Fig.1 Three types of leak holes

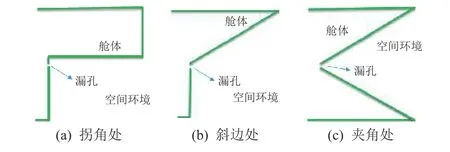
圖2 漏孔處于空間站外部不同位置示意Fig.2 Locations of leak holes in the external structures of the space station

2 DSMC仿真

在描述氣體粒子隨機運動的過程中需要運用DSMC方法[9]，并作如下假設：

1）入口氣流模型

氣體通過漏孔進入流場，其中的氣體粒子在孔口處均勻分布，粒子運動速度遵循麥克斯韋分布，分布函數為

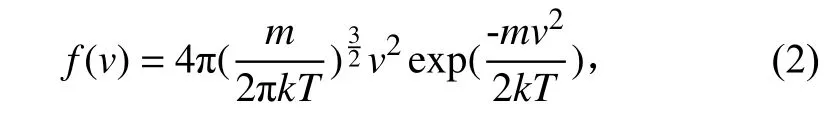
粒子運動方向按照余弦定律計算。

2）氣體粒子與壁面碰撞模型

氣體粒子穿過漏孔時，會與漏孔的內壁發生碰撞。粒子與漏孔內壁之間相對運動的物理模型采用完全漫反射模型，粒子飛離壁面時的方向符合余弦定律，速度服從麥克斯韋分布，分布函數如式(2)所示，平均動能與壁面溫度T有關。

3）氣體粒子間碰撞模型

氣體粒子間的碰撞模型采用可變硬球（variable hard sphere, VHS）模型[9]，對于稀薄氣體來說，粒子的平均碰撞率由玻耳茲曼方程

給出。式(3)中：n為氣體粒子數密度；σT為碰撞截面；cr為粒子間的相對運動速度。網格單元內粒子發生碰撞的概率pcol與σT、cr的乘積成正比[10]，

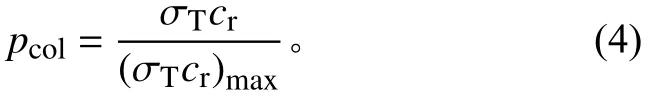
在VHS模型中，σT為cr的函數，而非恒定值，因此可以保證碰撞概率在[0, 1]之間。選擇合適的時間步長，即可求出在Δt內網格單元內發生的碰撞次數

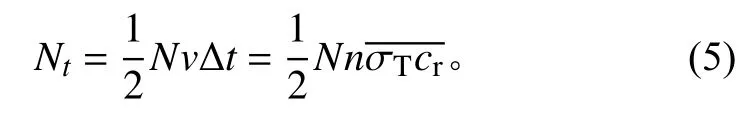
式中：N為單元內的總粒子數，其前面的系數1/2是表示2個粒子間才能發生相互碰撞[10]。

DSMC方法所采用的碰撞描述為非時間計數（NTC）法[9]，可在保持時間計數（TC）法[9]效率的同時克服TC法中的困難，并在程序開始之前事先計算出網格單元內的碰撞數。因此，可在運行碰撞程序之前預先對碰撞數進行標定，以提高運算效率。

由于空間真空環境的本底粒子密度相比于泄漏氣體密度可以忽略不計，本文模擬中不考慮泄漏氣體粒子與外部空間本底粒子的碰撞。粒子流物理模型的建立是為了在追蹤氣體分子運動時排除其他因素對追蹤的影響，相對獨立地計算氣體分子的運動情況。在模擬大量粒子的運動時，每一個粒子的運動由一組隨機變量來表達；對整個物理過程進行模擬時，進行抽樣的隨機數一般都在(0, 1)區間內服從均勻分布并且相互獨立，每個氣體粒子運動過程的模擬利用數學方法進行[6]。追蹤每個模擬粒子，記錄其位置和速度信息，然后對每個網格單元內的信息進行統計即可得到相應的流場壓力關系。

3 空間站泄漏總體分析

3.1 漏孔孔徑對羽流的影響

不同直徑下的圓柱形漏孔，達到穩態后的泄漏羽流場如圖3所示。可以看出，孔徑對泄漏的影響較大，孔徑越大漏率越大，羽流的形態會更飽滿，羽流場的平均壓力也就更大；且壓力沿軸向單調遞減，沿豎直方向對稱分布，向兩邊遞減。

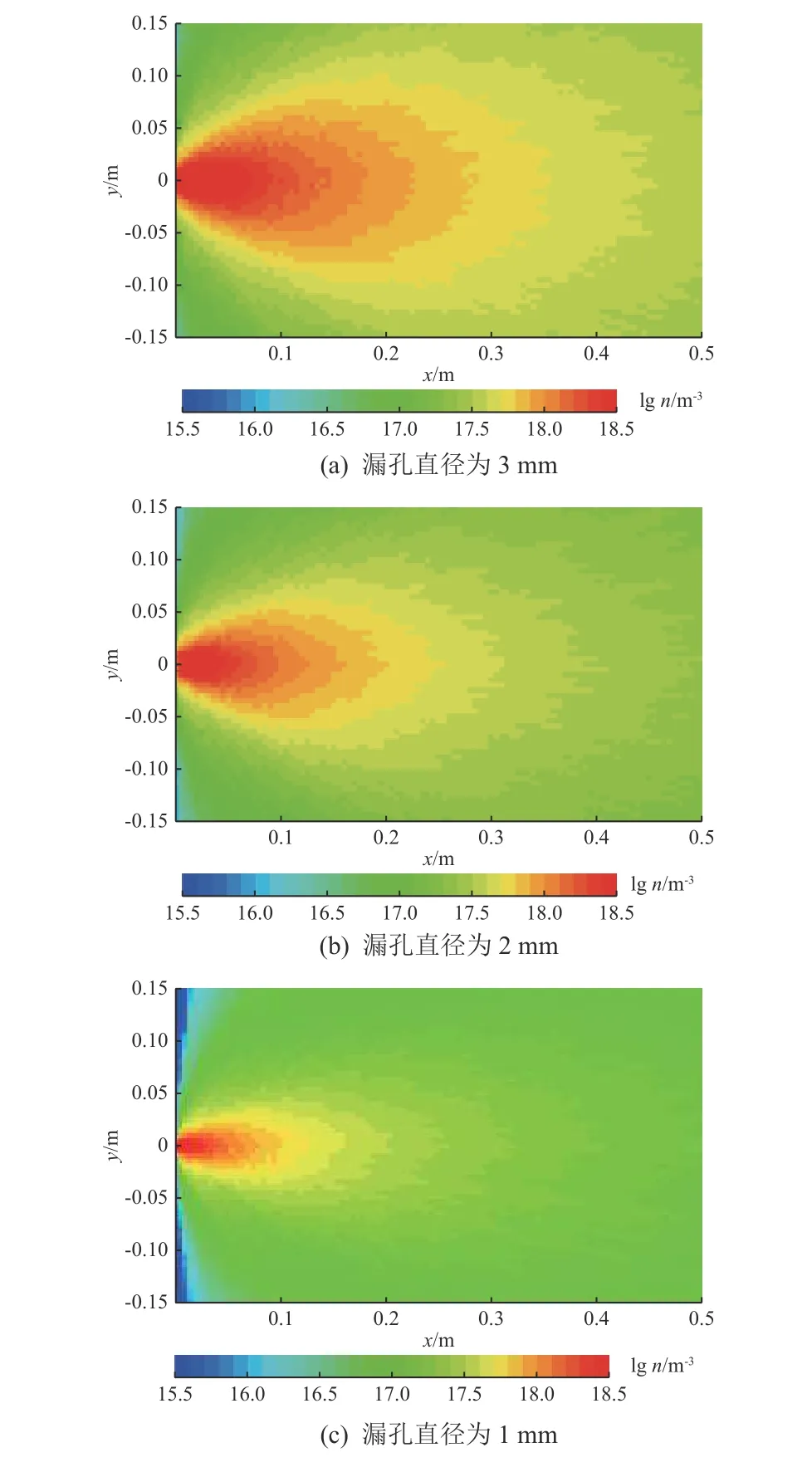
圖3 不同孔徑漏孔的羽流場Fig.3 The plume fields for leak holes of different diameters

3.2 漏孔形態對羽流的影響

當漏孔中間直徑為1 mm時，不同漏孔形態下達到穩態后的泄漏羽流場如圖4所示。可以看出，孔口形狀對漏率的影響較小，但均會在一定程度上改變羽流的形態，張口孔比縮口孔的羽流場平均壓力略微大一些，猜想可能是由于縮口孔的結構會對氣體有阻擋作用，導致氣體與壁面的碰撞次數增多，通過漏孔的粒子數減少。平行斜邊的漏孔結構會顯著改變氣體粒子運動的方向，使得羽流場偏轉一個角度，不再是對稱結構。

圖4 不同形態漏孔的羽流場Fig.4 The plume fields for leak holes of different shapes

3.3 航天器外部形狀對羽流的影響

不同位置漏孔處達到穩態后的泄漏羽流場如圖5所示。可以看出，航天器的外部形狀對羽流場的分布有較大的影響：拐角處的漏孔，泄漏氣體粒子受到外部壁面的限制，與壁面發生碰撞后被反射，使羽流形態發生改變；斜邊處的泄漏羽流會發生角度偏轉；而對稱夾角處的泄漏羽流場仍然保持對稱形態，無明顯改變。

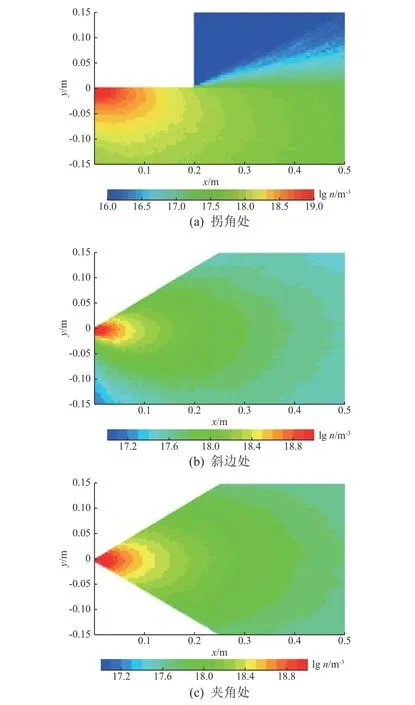
圖5 不同位置漏孔的羽流場Fig.5 The plume fields for leak holes at different locations

4 結果與討論

圖6是不同孔徑漏孔泄漏羽流的軸向粒子數密度隨軸向距離的變化。可以看出，軸向粒子數密度單調遞減，距漏孔越遠密度越小。

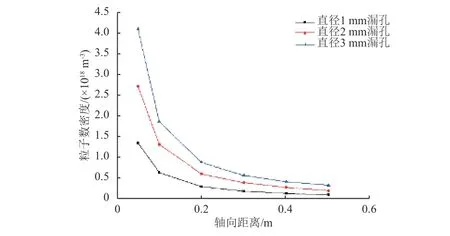
圖6 不同孔徑漏孔的軸向粒子數密度分布Fig.6 Number density distribution for leak holes with different diameters in axial direction

圖7是張口孔和縮口孔的軸向粒子數密度分布對比，前者比后者要大5×1016/m3左右。

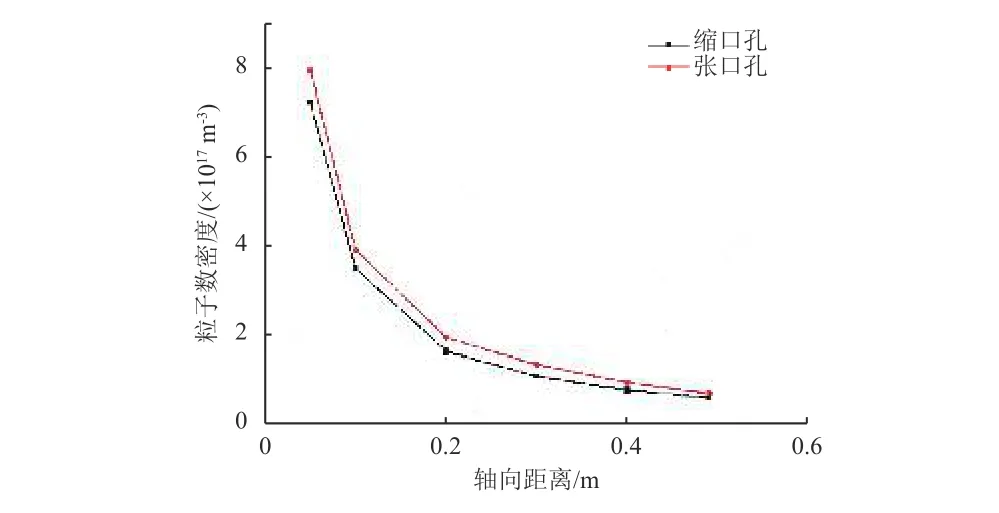
圖7 張口孔和縮口孔的軸向粒子數密度分布對比Fig.7 Comparison of number density distribution in axial direction between bellmouth orifice and funnel-shaped orifice

圖8是中間孔徑1 mm的漏孔泄漏達到穩態時，軸向距離分別為 0.1、0.2、0.3、0.4 m 處豎直方向的粒子數密度分布，可以看出粒子數密度在中間軸線處最高，向兩邊呈現遞減的對稱分布。因此，對于一般的漏孔，檢漏設備在可疑位置處的豎直方向進行測量，測得的峰值位置即處于漏孔的軸線方向，該點與艙體的垂直交點即為泄漏點；對于形狀不規則的漏孔，需對其豎直方向進行多次測量，獲取每次測量的峰值點，這些峰值點的連線與艙體的交點即為泄漏點。

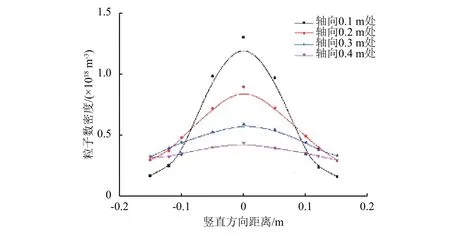
圖8 豎直方向粒子數密度分布Fig.8 Number density distribution in vertical direction

由3.3節可知，空間站的外部形狀會顯著改變泄漏羽流場的形態。為了能夠適應局部的羽流場分布，在空間站的管道交接處、艙體邊緣等位置進行檢漏測量時，檢漏設備要以一定的角度安放，并根據測量位置所處的幾何結構進行旋轉和移動，以便精準定位泄漏點。

5 結束語

本文采用DSMC方法，獲得了不同條件下，密封艙內氣體從不同漏孔中泄漏到真空環境中的羽流場分布，并對不同情況下的檢漏測量提出了建議。由于只進行了二維場模擬，與實際的三維空間粒子運動軌跡以及壓力分布會有所區別。后期將開展相關的縮比實驗，并將實驗結果與模擬仿真結果進行比對，以期獲得更加準確有效的泄漏測量及定位方法。為保證羽流的形成，選擇的實驗腔體要模擬在軌條件，因此要盡可能的大，以減少氣體與器壁的碰撞；另，抽氣系統需要提供均勻抽氣，如令整個腔體的壁面都為低溫冷面吸附氣體，以降低抽氣對氣體粒子運動的定向作用。