擴散聲場作用下C/SiC復合材料薄壁結構的全頻段響應分析

張永杰，陳利斌，張菩仁，王 喆

（1. 北京強度環境研究所，北京 100076； 2. 中國船舶工業系統工程研究院，北京 100094）

0 引言

航天器在飛行過程中會受到嚴酷的噪聲載荷作用[1-2]，其主要來源包括發動機的噴流噪聲和湍流邊界層引起的脈動壓力噪聲。前者主要在發射和起飛階段產生，后者則是再入、巡航階段最重要的噪聲來源。噪聲載荷會引起結構振動和交變應力，不僅會影響航天器重要儀器設備的正常工作，而且會導致結構的疲勞破壞[3]。新一代航天器中大量采用復合材料，使得聲致振動頻帶寬（10 Hz～10 kHz）、量級大，因此，進行大量級、寬頻帶噪聲載荷作用下的結構全頻段應力場分析，并通過結構設計加以控制具有非常重要的意義。

聲振響應計算方法主要有邊界元法、有限元法、統計能量法以及混合模型法等。用有限元法和邊界元法進行時域分析可得到結構具體位置的位移、速度、加速度以及應力等動態響應結果。但航天器所經歷的聲振環境覆蓋整個高中低的全頻段，使用有限元法和邊界元法進行計算時，一方面模型的單元數量會隨著頻率的增大而急劇增加，導致計算成本過高；另一方面有限元法和邊界元法是基于結構的確定性物理參數，而實際工程結構的真實參數與其名義參數有所不同，且高頻振動時結構對于物理參數微小的變化都非常敏感，會導致計算結果與真實響應結果間存在較大的偏差。因此，有限元法和邊界元法并不完全適用于全頻段的聲振響應分析[4]。統計能量法（SEA）主要用來預測噪聲激勵下的結構振動響應及內部噪聲情況，彌補了有限元法在聲振響應分析領域的不足，主要應用于結構振動響應的高頻段分析[5-6]。為了進行全頻段的聲振響應分析，混合模型方法的研究逐漸興起[7-8]，其中有限元-統計能量混合模型法（hybrid FE-SEA method）與其他方法相比具有更廣泛的工程適用性和發展前景，已成為聲振分析的一種有力工具[4,9-10]。

統計能量分析中的變量是子系統的振動能量，主要依賴于子系統的振動速度均方根值，因此，使用有限元-統計能量混合模型進行聲振響應分析，主要是計算結構的加速度響應[9-12]，關于聲振的應力場分析研究較少。而復合材料與各向同性材料的力學本構關系不同，其聲振應力場分析頗為復雜。這些均給通過聲振應力場進行航天器疲勞分析的研究帶來困難。

本文著眼于擴散聲場作用下復合材料薄壁結構的全頻段應力場分析，在混響室內進行自由狀態下的C/SiC復合材料薄壁結構的噪聲試驗；建立擴散聲場與正交各向異性復合材料薄壁結構相互作用的有限元-統計能量（FE-SEA）混合模型；基于模態應力恢復方法獲取結構應力場分布結果并進行分析。

1 模態應力恢復方法

在模態空間中，結構的位移可由模態振型及模態坐標的線性組合表示為[13]

式中：M、C、K分別為質量矩陣、阻尼矩陣和剛度矩陣；q為模態坐標；為模態振型。

根據模態應力恢復理論，隨機載荷下的模態響應可以模態互譜矩陣Sqq表示為[13]

式中E代表平均。若考慮n個模態，則Sqq(ω)為n×n階矩陣。

假設在有限元某節點i上，力和應力等響應量的個數為m，則它們的均方值響應為

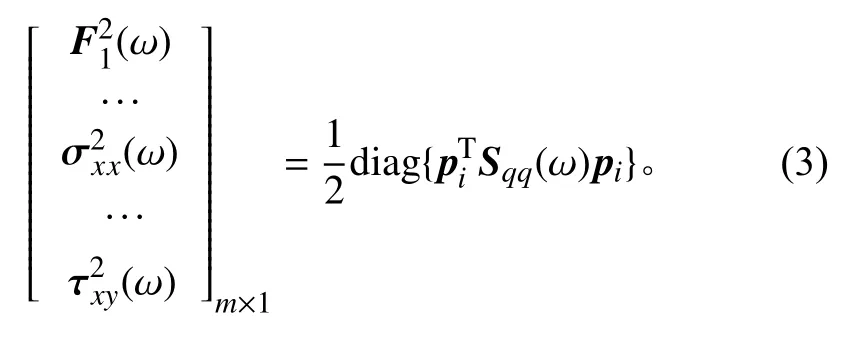
式中pi表示節點i上的模態坐標矩陣，為k×m階矩陣。

如果求得有限元模型中某節點的模態應力矢量為

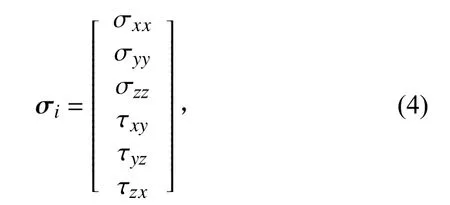
則Von Mises應力的RMS值為

式中：trace表示矩陣的跡，定義為矩陣對角線上的元素之和；對稱矩陣A的定義為

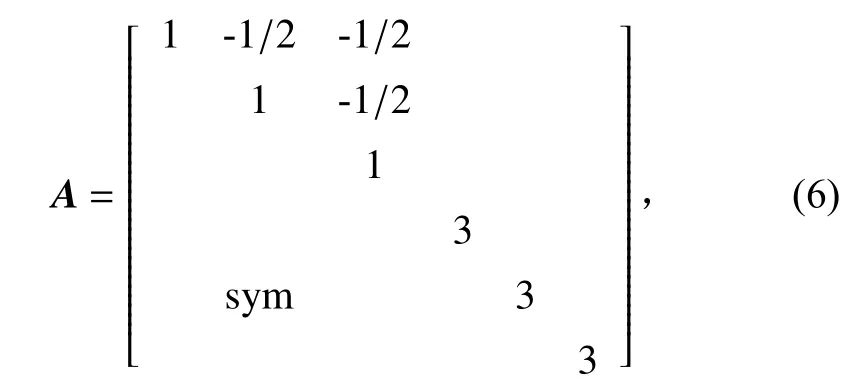
式中sym表示A的對稱元素。

2 混響室噪聲試驗

整個噪聲試驗系統由混響室、氣源、聲源、聲譜控制、聲測量和結構響應測量6個主要子系統組成。試件為厚度1.5 mm的C/SiC復合材料薄壁結構，長380 mm、寬260 mm，通過橡皮繩懸吊在70 m3混響室內，模擬自由邊界條件。C/SiC復合材料為正交各向異性材料，其力學性能參數如表1所示。

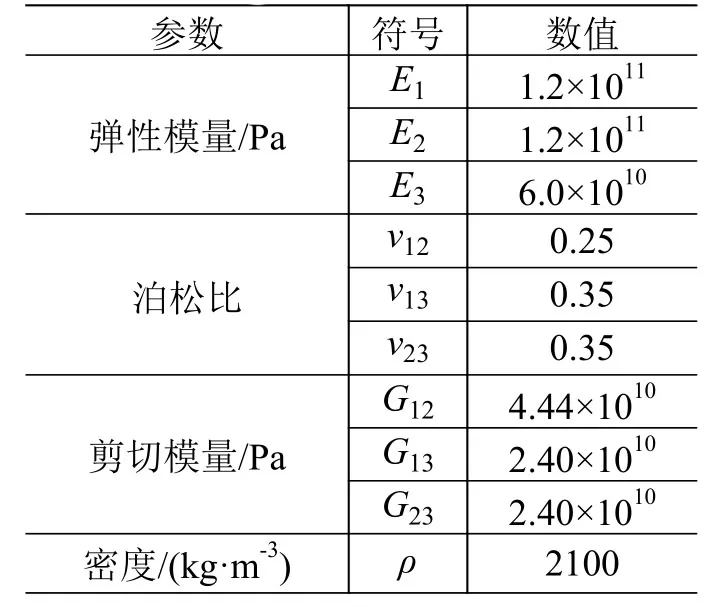
表1 C/SiC 復合材料力學性能參數Table 1 Mechanical parameters of the C/SiC composites

在復合材料平板上布置3個振動傳感器進行平板的聲振加速度響應測量，以平板的幾何中心為原點，3個加速度測點的坐標分別為(40, 95)、(-40,-95)和(45, -95)，單位mm。在平板的附近和周圍布置傳聲器，進行聲場測量。試驗設備及測點位置如圖1所示。混響室噪聲試驗中加載的總聲壓級為140 dB，在聲載荷以及結構響應穩定后，測量混響室內擴散聲場以及C/SiC復合材料薄板上的振動加速度響應。混響室內傳聲器獲取的聲譜如圖2所示。

圖1 C/SiC復合材料薄壁結構的混響室噪聲試驗Fig.1 Experiment of C/SiC composite thin plate structure in the reverberant chamber

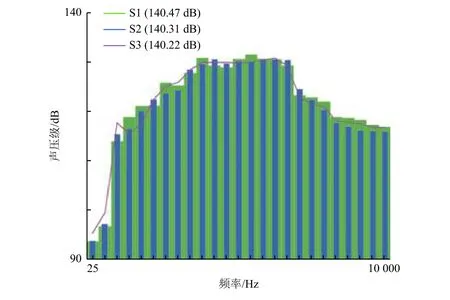
圖2 140 dB噪聲載荷下聲場測點聲譜Fig.2 The sound spectrum of the diffusive sound field (SPL=140 dB)

3 FE-SEA混合模型

使用正交各向異性材料本構關系，建立1.5 mm厚C/SiC復合材料薄壁結構的有限元模型并求解模態。模態頻率的試驗結果與計算結果如表2所示，各階模態振型的試驗與計算結果較為吻合，表明該有限元模型在低頻段是準確的。

表2 自由狀態模態頻率試驗與計算結果對比Table 2 Comparison between the tested and calculated modal frequencies under free boundary conditions

對混響室內3個傳聲器獲取的聲譜求平均，作為聲載荷（如圖3所示）。在VA One軟件中使用有限元子系統對薄壁結構進行建模，使用半無限流體（SIF）統計能量子系統對聲輻射的空氣進行建模，使用擴散聲場（DAF）進行聲載荷施加。最終建立的擴散聲場環境下的FE-SEA混合模型如圖4所示。

圖3 擴散聲場載荷Fig.3 Loading of diffusive sound field

圖4 混響室噪聲試驗的FE-SEA混合模型Fig.4 Hybrid FE-SEA model for acoustic test in the reverberant chamber

4 應力場及加速度響應結果分析

計算得到薄壁結構8000 Hz以內的加速度響應均方根分布云圖如圖5所示，可以看出：除了4個尖角位置的響應最大外，板的邊沿和中心區域的振動響應也較大，其加速度均方根值在9g～14g之間，其他區域則在5g～9g之間。計算結果與試驗結果吻合。

圖6所示為加速度測點3和對應位置的計算功率譜密度的對比曲線，可以看出：在整個分析頻率范圍內，2條曲線的變化趨勢以及峰值位置一致，但在100 Hz以下差別較大。這是由于試驗測試中結構懸吊邊界引起結構整體的振動響應。

圖7所示為基于模態應力恢復方法計算的擴散聲場作用下C/SiC復合材料薄壁結構的應力場分布云圖。其中Mises應力均方根值的最大和最小值分別位于平板的短邊中央和四角。通過圖5與圖7的比較可以看出，擴散聲場作用下的復合材料薄壁結構的應力場分布與加速度場分布規律并不相同。

圖5 加速度響應均方根值分布云圖Fig.5 Cloud map of root mean square value of acceleration response

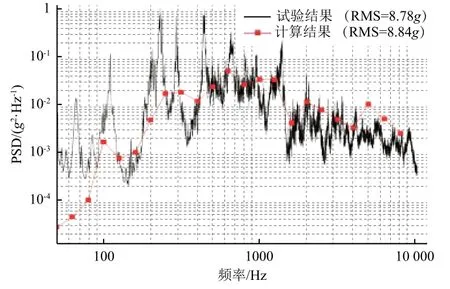
圖6 加速度響應計算與試驗結果對比Fig.6 Comparison between the simulation result and the experimental result of acceleration response

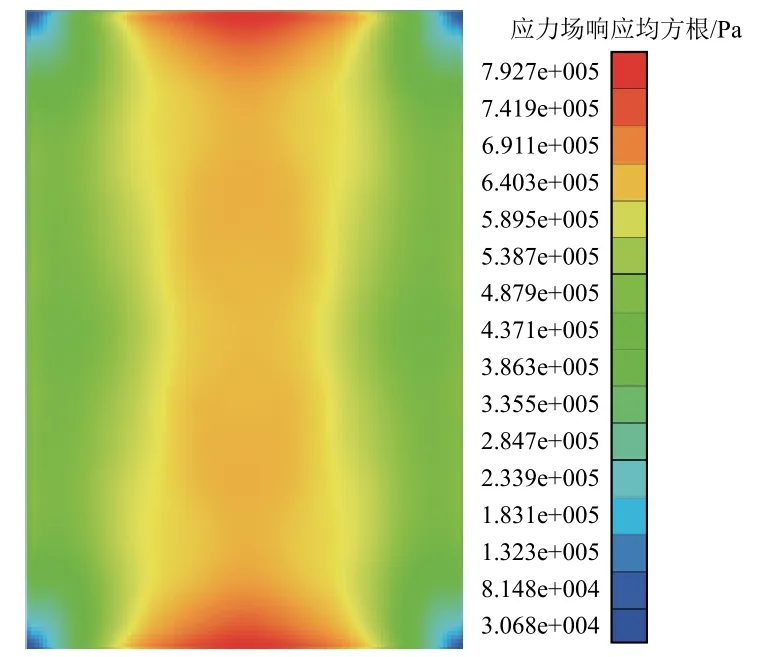
圖7 應力場響應均方根值分布云圖Fig.7 Root mean square value field of the Von Mises stress

圖8所示為噪聲場聲譜、聲載荷到結構的輸入功率以及結構輻射到空氣中的功率曲線。可以看出：相對于擴散聲場載荷，結構吸收的功率在以100 Hz為中心頻率的頻帶內有1個峰值，并且在1500 Hz以后吸收聲能較多，在以5000 Hz為中心頻率的頻帶內有1個峰值。表明結構在以100 Hz為中心頻率的頻帶內吸收功率較多，而輻射功率很小，從而形成響應峰值。結構輻射到空氣中的功率在以5000 Hz為中心頻率的頻帶內出現了峰值，表明在該頻帶內結構不僅能從聲場中吸收大量能量轉化為結構的振動能量，而且向空氣中輻射較多聲能量，即該頻帶內聲場與結構的波長耦合效應最強。

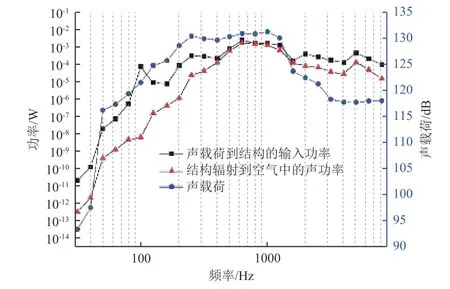
圖8 擴散聲場聲譜、聲載荷到結構的輸入功率以及結構輻射到空氣中的聲功率曲線Fig.8 The sound spectrum of the DAF, the power input of DAF to the structure, and the structure's acoustic radiation to the SIF

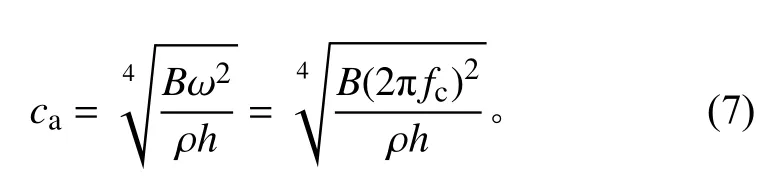
式中：B為彎曲剛度，B=Eh3/[12(1-ν2)]，其中，E為彈性模量，h為薄壁厚度，ν為泊松比；ω為圓頻率；ρ為材料密度；fc為臨界頻率。

C/SiC薄壁結構的振動以面內彎曲振型為主，將C/SiC薄壁結構的厚度和材料參數（彈性模量E1和泊松比 ν13）代入式(7)，計算得到臨界頻率為5262 Hz，處于以5000 Hz為中心頻率的頻帶內。說明在臨界頻率處，結構振型能夠與聲場發生很好的耦合，結構不僅能從聲場中吸收大量能量，而且能向空氣中輻射較多聲能。

5 結束語

本文針對擴散聲場作用下復合材料薄壁結構的全頻段應力場分析問題，在混響室內進行自由狀態下的C/SiC復合材料薄壁結構的噪聲試驗；建立了擴散聲場與正交各向異性復合材料薄壁結構相互作用的有限元-統計能量混合模型；并基于模態應力恢復方法計算得到了結構的應力場分布；通過分析復合材料薄壁結構的彎曲波長與聲波波長之間的關系，揭示了噪聲載荷與結構的波長耦合效應。

研究結果表明：模態應力恢復方法可用于全頻段聲振應力場分析的FE-SEA混合模型中，該模型計算的應力場可進一步用于聲疲勞分析。