數形結合思想在小學數學教材中的應用分析
——以人教版為例

熊慶

（長江師范學院 文學院，重慶 408000）

一、課題的提出

新課程標準修改后，將“雙基”改為了“四基”，即基礎知識、基本技能、基本思想方法、基本活動經驗，這就說明了人們已經意識到數學思想方法的重要性。這一轉變并不是偶然的，而是縱觀小學數學學習內容和小學生的認知特點而決定的。常用的數學思想方法之一就有“數形結合”思想。

數與形一直以來都是數學的主題，即使如今的數學有著龐大的分支，仍不可磨滅它的影響力。華羅庚先生的打油詩：“數無形，少直觀；形無數，少入微”向我們展現了數與形密不可分的關系。簡單的說，數與形就是抽象與形象的表現，數是形的抽象概括，形是數的直觀表現，數形結合更加有利于學生對知識的理解，單純的數使知識缺乏直觀性，同樣的如果只有形就少了幾分嚴密性，由此可見只有將“數”與“形”結合起來才能發揮出巨大的作用。

二、應用分析

數形結合思想在小學數學教材中有著許多巧妙的應用，如下：

表1 數形結合思想在教材中中的應用統計圖

問題解決images/BZ_74_1814_720_2263_1003.png四年級下冊（追擊問題）images/BZ_74_1814_1019_2270_1281.png

（一）數形結合體現在看圖提取數學信息

分析：這個例題中，首先情境很好地展現了“形”，以我們生活中熟悉的風箏作為素材，圖中的對話包含了數學信息，在每個風箏上標出了價格，提出數學問題，這就將“數”展現了出來，而不是直接以應用題的方式將條件和問題呈現出來，所以從這道題可以看出來數形結合思想不僅讓學生學會從“形”中提取“數”，還加深了學生對數的理解。這類題目的出現，充分體現了素質教育的全面推廣，數形結合思想的結合幫助提高學生的學習能力。

（二）數形結合思想體現在關于數的認識

分析：這道題是1~5的認識，在小學階段，數學的學習是從認識數開始的。低段的小學生大腦沒有發育完全，抽象思維對他們來說比較困難，在此表現的數形結合就是將抽象的數字與小朋友日常生活中比較熟悉的事物聯系起來，也就是他們熟悉的“形”，比如1就像鉛筆一樣是細長的，2的形態就像一只水中的鴨子，3的形態就像耳朵在聽聲音，4的形狀就像彩旗迎風飄，5的形狀就像秤鉤彎彎的，將“形”與 “數”共同點找出來，這樣就將“形”與“數”很好的結合在了一起，以便于小朋友記憶。

分析：這道題是認識億以內的數，對我們成年人來說無疑是非常簡單的，但是對于小學生而言，他們只知道大數很大，很多，沒有具體的概念，這個時候就需要我們把數位在形象的圖上表示出來，大數首先從數位上來說就很多，不好讀，所以單就讀數來看，用圖形來讀數明顯降低了難度，比如，在萬位上放一顆珠子，就表示一萬，放十顆珠子就表示十萬，滿“十”就可以進“一”到下一位數位，也就是在十萬位上放一顆珠子表示十萬，這樣圖形也幫助小朋友很直觀地理解數位。

由上面兩道題來看，數形結合在數的認識方面起到了非常直觀形象的作用。

（三）數形結合思想體現在關于數的運算

給出的題目是這樣的：二（1）班有35人，二（3）班有37人，一共有多少名學生？

列出算式: 35+37

分析：圖片中給出的一捆小棒代表的是十，一根小棒代表的是一，35也就是三捆小棒再加五根小棒，37就是三捆小棒再加七根小棒，圖片中是將整捆小棒放在一起，也就是有六捆小棒代表60，再將七根小棒拿出五根，余下兩根，與旁邊的五根小棒放在一起剛好湊成一整捆也就是十，那現在也就是有七捆小棒，代表70，還剩兩根小棒，代表2，一共就是72。用一整捆小棒這個“形”來幫助理解進位，讓學生直觀地認識到“滿十進一”的算理，最終會解這個“數”，在這個過程中也是將“數”與“形”有機地結合在了一起。

（四）關于問題解決

例4 小明和余小紅兩家相距12km，兩人同時出發同向而行去少年宮，小紅步行每小時4km，小明在后面騎自行車，每小時的速度是小紅的3倍，問多久后小明追上小紅？

解：小明追上小紅，從圖中我們可以發現小明比小紅多行12km，以這個為切入點進行計算。

小明的速度比小紅快 4×3－4=8(km/h)

小明比小紅多走12km，即所花時間為 12÷8=1.5（h)

答：一個半小時后邵明追上余伊。

分析：這是一個追擊問題，如果直接給學生分析題目，一兩句話也解釋不清楚，許多同學會覺得亂，這時候可以用畫圖使題目清晰，追擊問題是小學數學應用題中一個重要板塊，它可以變化各種各樣的形式，且難易各異。解決這類問題，好的邏輯思維能力非常關鍵，但由于題中信息量的原因，很容易讓人搞不清頭緒。線段圖的出現即簡單描述了情境，又將重要信息標注在上面，就本題而言，線段圖幫助學生找出等量關系，如“小明比小紅多行12km”，從而列出等式。

例5 張建在班級的讀書角借了一本書，這本書一共有300頁。一段時間后陳新也想看這本書，可他只看了書的2/5，剩下的部分如果要在6天內看完，然后把書給陳新，張建平均每天要看多少頁？

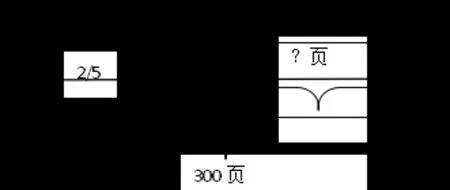
解：1-2/5=3/5 300*3/5=180（頁），180÷6=30（頁/天）。答：張建平均每天要看30頁。

分析：這樣的現象在小學是非常常見的，小朋友們常常喜歡看同一本書，遇到類似的問題你能巧妙地解決嗎？其實就是把學生生活中的問題轉化為數學問題，動員大家思考討論，看看能否解決。線段圖只是將數學信息具體化的一種方式，這種數轉化為形最大的好處就是直觀具體，從小學就開始培養數形結合的意識，有利于學生養成這樣的習慣，今后即使遇到更加復雜的問題時也不至于手忙腳亂，有更多的思路去解決。

三、總結、啟示

由以上“數形結合”思想在小學數學教材中的應用分析來看，教材中很多地方都用到了這種數學思想，從低段到高段的教材中均有滲透，這就說明了“數形結合”是小學階段的一個重要手段，今天我所分析的只是一些初步的、淺顯的認識，從長遠來看，這一重要數學思想勢必對學生們今后在初、高中的學習構建空間思維將起著關鍵作用。合理、巧妙地在小學數學教材中應用“數形結合”思想，不僅可以為教材的編排深度開辟一片廣闊的天地，緊跟新課標改革的步伐，還能為學生的終身學習和可持續發展奠定扎實的基礎。