求解LTI 系統零狀態響應過程中的解法辨析
2019-08-23 10:41:30馬丁
數字通信世界 2019年7期
馬 丁
(南昌航空大學科技學院,南昌 330034)
由線性時不變(LTI)系統的特性可知,其零狀態響應yf(t)等于輸入信號f(t)與系統的單位沖激響應h(t)的卷積。即如果已知單位沖激信號δ(t)作用在系統上的響應h(t),利用卷積即可求得任意連續信號f(t)作用在系統上的零狀態響應。可見系統沖激響應的求解和卷積的計算是求解系統零狀態響應的關鍵。本文以h(t)的求解為重點,將兩種主流方法加以對比,并指出容易陷入的誤區。
例:求下列系統的零狀態響應
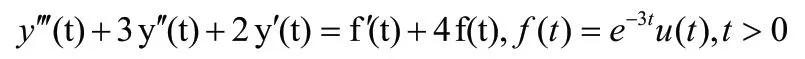
1 單位沖激響應h(t)
1.1 沖激平衡法


1.2 傅里葉反變換法


(2)H(jω)的表達式中后兩項均為單邊指數信號的傅立葉變換,故推測第一項求反變換之后不應出現符號函數這種特殊項。

另外用單邊拉普拉斯變換也極易求出上述結果。
2 零狀態響應yf(t)

3 結束語
求單位沖激響應h(t)時,用沖激平衡法及傅里葉反變換法均可得到正確的結果,前者過程繁瑣,后者較為簡便。但如果忽略了已知條件t>0的限制,單純地利用(-∞,+∞)上常見函數的傅里葉變換對來求反變換,往往會得到錯誤的結論,這一點需要格外注意。
猜你喜歡
工業設計(2022年8期)2022-09-09 07:43:20
鴨綠江(2021年35期)2021-04-19 12:24:18
軍民兩用技術與產品(2021年10期)2021-03-16 06:05:30
北京測繪(2020年12期)2020-12-29 01:33:58
考試與評價·高一版(2020年6期)2020-11-02 02:45:24
裝備制造技術(2019年12期)2019-12-25 03:06:46
中國洗滌用品工業(2019年4期)2019-05-11 09:27:34
中國生殖健康(2019年3期)2019-02-01 06:12:26
家庭影院技術(2017年9期)2017-09-26 03:41:45
鑿巖機械氣動工具(2016年3期)2016-03-01 04:00:25

