借助輔助圓 提升三角形問題解決效率
張 健
(江蘇省海門市東洲國際學校 226100)
圓作為特殊的平面曲線圖形,其特殊性質可以幫助學生們提高一些常規方法難以解決的問題,實現問題的降級化、簡單化.借助構造的輔助圓,讓看似與圓無關的較難問題、抽象問題轉變成簡單、形象的問題,實現問題的快速解決.本文就詳細講解在三角形中,如何通過構造的圓,來促進問題的解決.
一、構造圓,證明不等式問題
圓因其自身的特殊性質,不僅是初中數學中需要掌握的重要內容,也是幫助學生們解決某些數學問題的橋梁.有關三角形不等式的求解方法很多,但是當正面求解較為困難時,可以借助構造的圓來解決.妙用三角形的內接圓也可以降低原問題的難度.
例1已知三角形ABC中的∠BAC=90°,AD是斜邊BC上的高,證明:AD+BC>AB+AC.
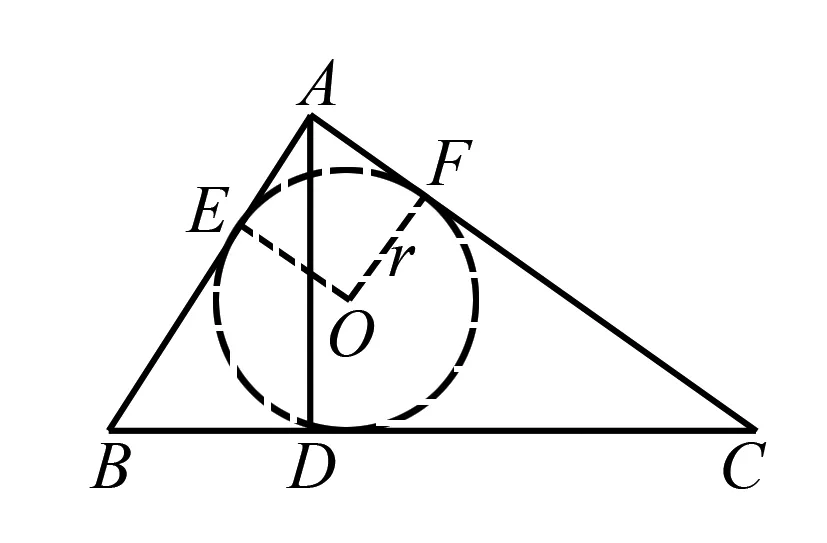
圖1
證明令Rt△ABC的內切圓的半徑是r,如圖1 ,因為AB+AC=BC+2r,又2r
反思此題需要知道三角形內接圓與邊之間的等量關系,r=(a+b-c)/2,即轉化為本題中的AB+AC=BC+2r.幾何不等式證明常規思路是截長補短,但需要借助構造的全等三角形或者比例線段來求解,技巧性很強,而借助輔助圓則避免了這一弊端,實現數形結合幫助理解.
二、輔助圓,簡化角度求解
借助三角形的外接圓可以簡化某些問題,同樣,通過構造的圓也可以簡化三角形角度求解問題.一般將三角形的公共定點當做是一個頂點,然后作出三角形的外接圓,搭建起等角和輔助圓中有關角度橋梁,實現問題的解決.
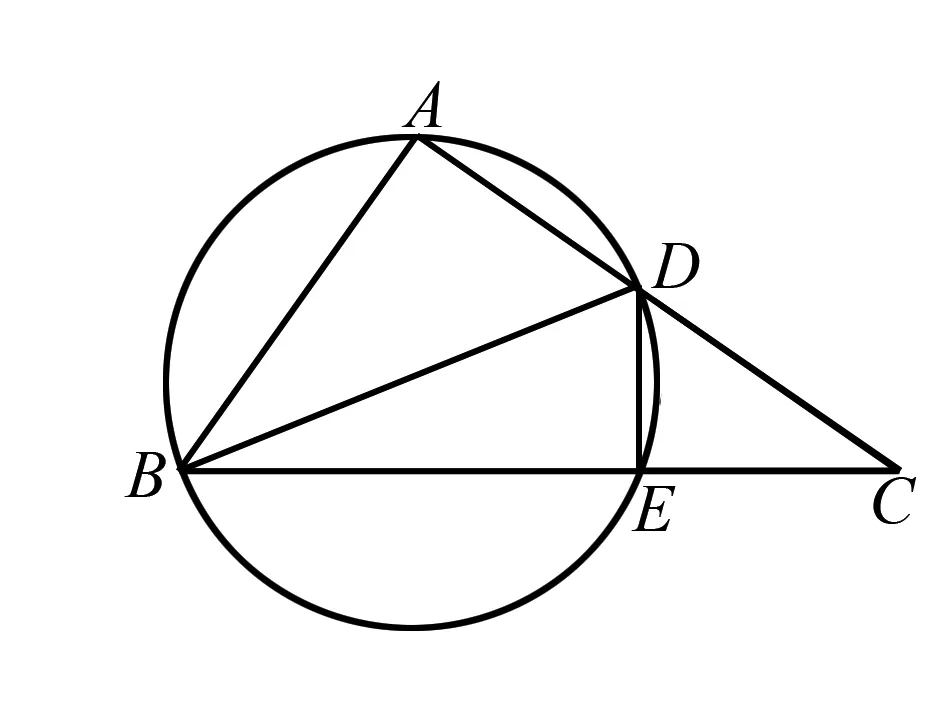
圖2
例2 如圖2,在△ABC中,AB=AC,且 ∠ABC的角平分線與邊AC相交于點D,且BD+AD=BC,求∠A的度數.
解析根據題意知,BD是∠ABC的角平分線,所以∠ABD=∠DBC.因此以BD為圓的直徑,作一個如圖2的輔助圓,交BC于點E,連接DE,所以AD與DE的弧長相等(同圓中相等圓周角所對應的的弧長相等).又四邊形ABED是圓的內接四邊形,所以

反思三角形中常見的構圓類型十分多,可以構造內接圓、外接圓、或者部分圓,究竟以哪個圖形為基礎構造何種類型的圓,都需要借助題目條件和問題進行多次嘗試,經過日常的積累和歸納總結,形成一定的解題敏感性和思維的發散性.通過構造的圓可以簡化三角形角度的求解;有關圓的性質需要熟悉并靈活運用,如圓周角、圓心角、弧長等;圓內接四邊形的性質也要準確把握.
三、借助圓,判斷三角形類別
三角形種類繁多,如正三角形、直角三角形等,每種特殊三角形都有自己的特殊性質,如正三角形的三條邊都相等、三個角都相等、中線垂直于對應的邊等特殊性質.判斷三角形的種類歸根結底是依據特殊三角形的角或者邊的關系進行判斷.但是,當已知條件錯綜復雜時,難以直接利用已有信息判斷時,可以借助圓來搭建橋梁,實現問題化簡和解決.
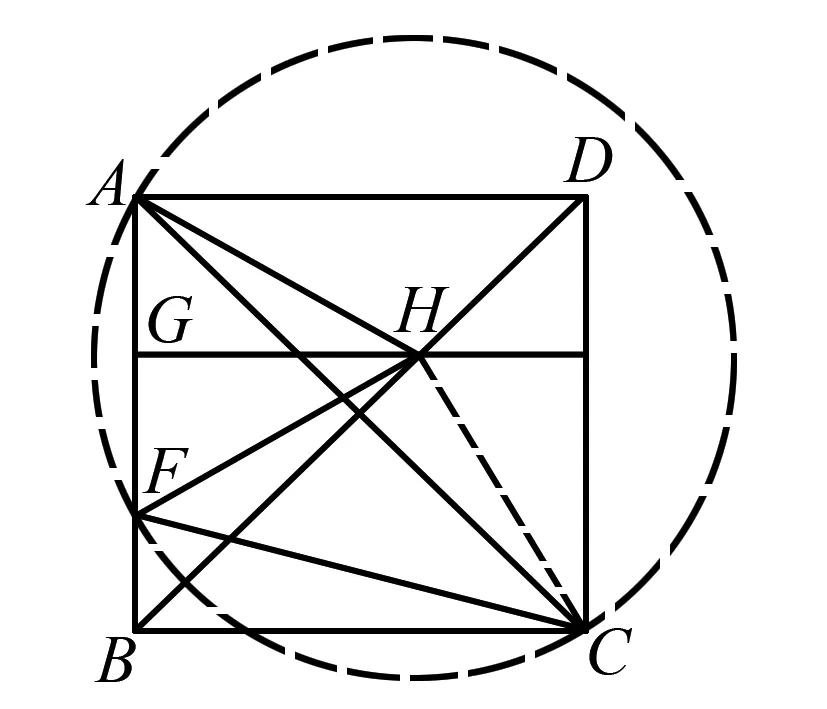
圖3
例3 如圖3,點F是正方形ABCD中AB上的一點,∠ACF=30°,AF邊上的中點G滿足GH∥AD,交BD于點H求證:△HAF是正三角形.
解析連接HC,則△DHA與△CHD全等,所以AH=CH.又GH∥AD,所以GH⊥AF.又G是AF的中點,所以GH是AF的中垂線,因此AH=HF,所以HA=HF=HC.以H為圓心,HA為半徑作圓H;則A,F,C在圓H上,則∠AHF=2∠ACF=60°,所以△HAF是正三角形.
反思有關圓的傳遞角的關系是極其重要的的內容,當問題含有三點距離某一個點距離相同時,可以考慮構造整個圓、部分圓,借助圓的性質與特殊三角形的性質,搭建橋梁,鋪設解題的道路;三角形、正方形等各種平面圖形的都可以進行結合形成復雜的圖形問題,因此,復雜問題的求解需要學生們熟悉掌握各種平面圖形的性質.
添加輔助線、構建基本圖形是證明平面幾何證明問題的法寶,輔助線添加的巧妙,往往會起到化腐朽為神奇,讓解題思路煥然一新.在三角形問題中,通過構建合適的圓,熟悉構造圓的情形和應用條件,借助圓和三角形知識有關知識,搭設題設問題與求解問題的聯系,得到解題的新思路、新方法,最終實現問題的快速求解與證明.

