基于致動線/BPM模型結合的風力機氣動噪聲研究

程 志，楊建剛

（東南大學 火電機組振動國家工程研究中心，南京 210096）

進入21世紀以來，全球風力機的發電功率在不斷増加，風資源開發已從沿海向內陸展開[1]。風資源開發距離居民生活區越來越近。同時，為了提高風力機的效率，風力機也一直在向大型化發展，其氣動噪聲也不斷增加，不可避免影響到居民的生活。

Nii和Yoshinor等[2]通過研究發現風電場在規劃和選址時，氣動噪聲是必須要考慮的影響因子之一。荷蘭、德國和丹麥等國家對風力機產生的噪聲水平是否影響周邊居民和動物生活進行過測量，發現風力機氣動噪聲對候鳥遷徙有很大影響[3]。同時音量和頻率等聲音參數的變化將會直接影響居民的身心健康。因此，風力機氣動噪聲也成為近來的研究熱點。

氣動聲學的研究主要分為直接模擬[4-6]和混合模擬[7-9]兩類。直接模擬方法雖然精度高，但其計算量巨大。混合模擬方法將流場與聲場的計算分開，更適合于復雜的工業模型，其中各種軟件中流場的計算方法已經相對成熟，但聲場模擬仍然相對滯后。除了經驗方法外，目前被廣泛使用的聲場計算方法是Lighthill聲理論[7]以及其延伸理論，可對翼型噪聲[8]、風力機近遠噪聲開展研究[9-12]。但該方法是基于 Lighthill、Lighthill-Curle 和 Ffowcs Williams-Hawkings方程，經過一定簡化后推導得到的解析解[13]，會忽略掉流場中一些壓強波動，造成誤差[14]，具有局限性。相比之下，利用原始聲學方程[15-16]進行微分計算更準確且適用面更廣泛，并且能夠展現出聲波向外傳播的過程[17]。目前國內的聲場研究仍然廣泛基于常用的積分法開展。本文聲場計算基于聲學擾動方程微分法展開。

在風力發電機的流場仿真計算中，致動線模型因為不用對風力機實體模型進行解析，免去了在葉片表面邊界層進行高精度解析的要求，對網格要求較低、計算速度快[18]，在風場遠場以及尾流計算中有很大優勢并被廣泛使用[19]。但致動線模型無法解析葉片邊界層，邊界層的翼型自噪聲聲源無法通過致動線方法獲得。BPM模型不包括尾流波動帶來的噪聲源，但可以提供在致動線模型中缺失的翼型自噪聲聲源，同時基于聲學波動方程計算聲場具有精度高、能夠展現聲波傳播過程等優點。因此本文將致動線方法和BPM模型進行結合來計算聲學擾動方程的聲源項。

本文以OpenFOAM為平臺，模擬點聲源擴散，并通過與聲學理論的對比，驗證聲學擾動方程以及代碼編寫的正確性；然后，基于致動線模型計算并分析某型號風力機的流場，同時基于BPM模型計算同一型號風力機的聲壓情況；最后，將根據致動線模型計算出的流場與根據BPM模型計算得出的聲源結合，作為完整聲源項放入聲學波動方程來計算聲場，對聲場的計算結果進行分析。

1 數值方法

1.1 不可壓縮混合RANS/APE聲場計算

本文聲場計算基于混合方法來開展，在該方法中，詳細的流體參數被分解成不可壓縮的流動變量及可壓縮的波動變量

式中：u′、p′和ρ′為瞬時不可壓縮速度、瞬時不可壓縮壓強和瞬時不可壓縮密度，U、ρ0和P分別為流場計算中得到的不可壓縮速度、不可壓縮密度和不可壓縮壓強。其中不可壓縮流動的參數包括了湍流流場的信息，后面的可壓縮波動參數代表聲場情況，本文風力機流場致動線計算基于RANS湍流模型。

當獲得不可壓縮流場信息后，便可以基于聲學擾動方程進行聲場的計算。Ewert在論文中提及了多種不同形式的聲波擾動方程[20]，本文使用的聲波擾動方程在某一維方向上表達如下

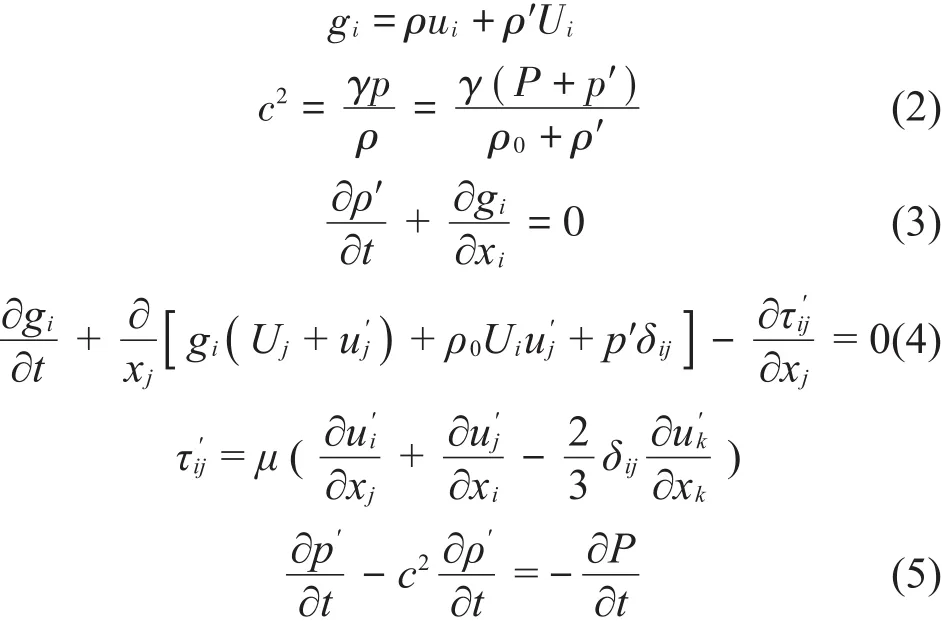
式中：i、j、k分別表示三維向量方向，APE方程左邊的波動參數包括了非穩態流動中聲場傳播的信息，方程的右邊涵蓋了聲源項，這里是來自流場的壓強變化為中間變量，c為聲速，δ為張量轉換因ij子為黏性力。關于聲學波動信息的傳播方程是從原始的可壓縮流動方程推導而來，需要從可壓縮流動方程中將不可壓縮部分除去[21]。由于空氣中的壓強擾動引起耳膜振動并經聽覺神經傳至大腦被確定為聲音[13，22]，得到流體波動參數后便可以得到聲音信息。APE聲學擾動方程已經在低馬赫數流動問題、湍流問題以及點聲源擴散問題中被驗證正確[23-24]。

1.2 致動線模型

致動線模型是一種計算風力發電機流場的常用方法。風力機的葉片旋轉時會施加氣動力給周圍的空氣，基于BEM葉素模型將葉片和周圍流體相互作用的體積力提取出來，然后施加到致動線模型的三維納維-斯托克斯控制方程中，用來替代葉片表面的負載。

式中：f為施加的體積力。

通過計算BEM葉素模型以及翼型參數，可以得到施加的體積力f[19]。BEM葉素模型將葉片沿著翼展劃分成連續的小段，然后將每一段葉素視為一個二維翼型。每段葉素的攻角由該段所在的速度三角形決定，每段葉素的升力和阻力由該段所在升阻力系數決定。該模型運用廣泛，數學原理在此不做闡述。

由于致動線模型無法解析葉片邊界層，邊界層的翼型自噪聲聲源無法通過致動線方法獲得。所以引入BPM模型來考慮翼型自噪聲聲源的影響。

1.3 制動線模型-BPM模型結合

對于翼型自噪聲，BPM模型是最常用的半經驗模型，由Brooks、Pope和Marcolini在實驗測試的基礎上提出[25]。翼型自噪聲又分為：湍流邊界層尾緣噪聲、分離流噪聲、層流邊界層渦脫噪聲、葉尖渦噪聲和鈍尾緣渦脫噪聲。每種噪聲類型都有自己的半經驗公式，在每段葉素上，通過半經驗公式提取得到10 Hz到20000 Hz中三分之一聲壓頻段的5種噪聲來源。來自于致動線模型的噪聲源仍然保留在式（5）中。這里通過高斯正則化對來自于BPM半經驗模型的噪聲源進行處理，同時為了避免數據計算產生奇異性，不能用聲源點聲壓替代，研究發現距離各段葉素一個弦長位置范圍內的聲壓已經保持不變，本文用距離各段葉素十分之一弦長位置的聲壓來替代該葉素所在位置的聲壓，然后轉換為波動壓強

然后式（5）被改寫為

式中：m為風力機葉片的數目，n為每段葉片被劃分的葉素數量，l為10 Hz到20000 Hz之間三分之一倍頻程頻率的數量，根據三分之一倍頻程的劃分規則，文中l為31。d(=|x-se|)仍為正則化過程中某坐標為(x,y,z)的網格中心點到對應致動線中心點的距離，?為BPM聲源波動壓強的高斯光滑系數。

2 算例與結果分析

2.1 點聲源擴散

先對基于聲學擾動方程的聲場計算進行驗證分析，將計算結果與空氣中點聲源的耗散理論進行對比驗證。計算域模擬邊長為200 m的的正方形擴散域，在正方形擴散域中心設置點聲源。時間格式采用Crank-Nicholson格式，其它如梯度格式、散度格式及拉普拉斯項格式等采用Gauss linear 2階格式。網格設置為4001×5×5，可以看出，Y方向和Z方向網格十分稀疏，在這兩個方向傳播的聲參數由于無法被網格識別會直接耗散。對聲音在X方向上的傳播情況進行分析，采集點在Y及Z方向上與聲源點的距離為0，在X方向上與聲源點的距離分別為2、4、6、8、10、20、30、40、50，單位是米，如圖1所示。

圖1 點聲源示意圖

將點聲源頻率設置為80 Hz，幅值一定，當計算時間達0.5 s時，聲場傳播到計算域邊界。t=0.4 s時的聲壓傳播截面圖如圖2所示，可以看出Y及Z方向的聲波被粗糙網格快速耗散。點聲源向四周傳播時波動壓強的數值越來越小。

圖280 Hz點聲源擴散t=0.4 s時壓強波動截面圖

根據點聲源在干燥空氣中傳播的斯托克斯聲衰減定律[22]，聲壓的衰減滿足公式

式中：A0可以為某點的聲壓，A()d為與該點距離為d的另外一點的聲壓，α與傳播介質、聲源形式以及傳播方式等有關，與聲源頻率的平方成正比，滿足α∝ω2。

將點聲源頻率分別設置為40 Hz、80 Hz、200 Hz及300 Hz，幅值相同，為一定值，其他模擬參數相同。表1是不同頻率點聲源傳播模擬中相鄰采集點間衰減指數α的變化情況。

圖3（a）是不同頻率點聲源傳播計算結果及其擬合曲線。結合表1及圖3（a）可以看出，低頻點聲源擬合情況優秀，高頻點聲源由于傳播衰減太快，遠距離時網格難以捕捉聲參數，模擬得出的高頻衰減指數在遠距離時有誤差。在另外的網格無關性驗證中發現，在工程噪聲問題分析中，由于高頻聲音衰減很快，進行遠場分析時可以不考慮，可以根據情況調整網格精度。

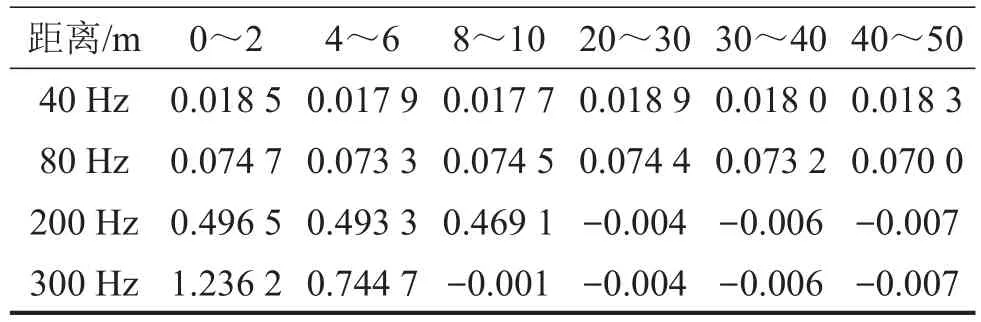
表1 不同頻率聲源相鄰采集點間衰減指數α的變化情況

圖3（b）展示了不同頻率噪聲衰減指數與頻率之間的關系，說明在某一網格精度下，噪聲衰減模擬滿足α∝ω2。可以看出，用文中基于APE編寫的OpenFOAM聲場求解器模擬聲源傳播時，符合衰減指數α與頻率平方成正比的斯托克斯聲衰減定律，基于聲學擾動方程的聲場計算結果正確。

2.2 NREL5MWRef風力機流場

驗證了聲場計算方法的正確性后，這部分以及下節將研究分析NREL5MWRef型號風力機的流場和聲場。NREL5MWRef型號風力機以及計算風場域的參數如表2所示。風場計算域如圖4所示。

表2 NREL5MWRef風力機參數

圖3 不同頻率點聲源傳播中采集點波動壓強

圖4 風場計算域示意圖

由于致動線模型和BPM模型的植入都不需要對葉片邊界層局部解析，并且下文基于聲學擾動方程的聲場計算需要在遠場保持相同的網格精度，結合研究經驗，平衡計算精度和時間后，沿整個計算域3個方向采用等距的200×200×60網格布置。流場計算中時間步長δt為0.05 s，時間微分采用Crank-Nicholson格式，其它離散如梯度格式、散度格式及拉普拉斯項格式等采用Gauss linear2階格式。在時間步t=80 s時，計算域內的非穩態流場已經完全被解析。此時流場的速度云圖以及湍動能云圖如圖5所示。

速度云圖分為3個扇區，對應3個葉片，反映了風力機葉片在旋轉過程中的速度變化規律。由圖5（a）可以看出，風力機葉片旋轉區域具有后面有明顯的速度下降、隨著距離越來越遠速度逐漸恢復的趨勢；本文設定風力機來流為均勻來流，故如圖5（b）所示，整體湍流強度低。但在風力機后面的位置仍然有明顯的湍流存在，并隨著距離越來越遠，湍流強度減輕。湍流的云圖趨勢和速度的云圖趨勢保持一致，并與實際情況相吻合。

圖6為風力機尾流的渦量等值面，能夠清晰反映尾跡流場的特點。由于NREL5MWRef型號風力機尺寸大，葉尖速比高，葉尖渦會迅速破碎耗散，且由于此時泄渦頻率很大，尾渦的螺旋狀結構相對小風力機不太明顯。

圖5 風力機流場

圖6 風力機渦量圖

該型號風力機暫時沒有對應的實驗數據，但致動線模型是一種很成熟的風力機流場計算模型。其正確性在以往大量研究中都有驗證，本課題組關于致動線模型流場也有大量的基礎工作。

2.3 NREL5MWRef風力機聲場

在前文得到的風力機流場的基礎上，加上從BPM模型中得到的聲源，進行聲場計算。時間微分采用Crank-Nicholson格式，其它離散如梯度格式、散度格式及拉普拉斯項格式等采用Gauss linear 2階格式。受計算量與計算時間的限制，時間步長δt取0.002 s，這對高頻噪聲的解析有一定影響，不過實際情況中高頻噪聲消減很快，在遠場分析時可以放在次要位置。該聲場計算以完全解析流場為起始點，采用并行計算，調用超算共75個2 G的CPU，計算時間3天。

人耳能夠識別的極限聲源頻率范圍為10 Hz到20000 Hz，故在從BPM模型中抽離聲源時，選擇10Hz到20000 Hz范圍內的三分之一倍頻程。圖7展示了從BPM模型中抽離出的20 Hz、200 Hz、1000 Hz和20000 Hz頻率聲源，由于葉片的偏轉，某一垂直截面上3個葉片的壓強云圖不一樣。

由圖7中可以看出，不同頻率情況下聲源的量級有很大差距，中間頻率部分的聲壓級水平更高；另外，葉片上聲源重心位置不同，這體現出葉片位置、聲源頻率以及發聲機理之間的關系。雖然不同頻率下聲源位置分布不一，但整體上呈現頻率越高、聲源重心越靠近葉尖位置的現象，這是因為葉尖位置與空氣的相對速度大，渦脫落頻率高，流場變化相對葉根更為劇烈，聲源頻率高。

圖7 不同頻率的BPM聲源聲壓云圖

圖8是波動壓強在不同時刻的云圖，體現了聲壓逐漸向外傳播的過程，最后再覆蓋到全域。聲音在空氣中擴散時，一方面隨著傳播球面的表面積越來越大，單位面積聲壓強度越來越小，同時由于空氣介質的吸收作用，攜帶聲音信息的粒子在介質中震蕩能量被消耗，高頻噪聲震蕩越快，消耗速度越快，所以高頻噪聲消散很快，從圖8中可以看出隨著聲壓的擴散，強度逐漸減輕。同時在靠近地面附近，由于聲壓的反射可以看到干涉情況出現，各截圖的底部為地面。

圖9為不同觀察點（-200，0，0）及（-100，0，0）處波動壓強的頻譜圖，點（-200，0，0）在風力機正上方。由于風力機的轉速是12.1 r/min，可以看到，各位置聲壓級的頻譜在該頻率附近能量很高，交織在一起，并且由于低頻衰減較慢，低頻聲壓級沒有什么差別。隨著頻率增大，可以看到點（-200，0，0）仍然呈現一定的波峰，這些波峰有相當一部分來自于從BPM半經驗模型中添加的噪聲源，但較遠處聲壓級的高頻部分迅速衰減，能量變小，這與聲源傳播的規律相一致。很多調查顯示，風場附近的居民對高頻噪聲的感知較弱，但風力機低頻噪聲產生的連續不斷的“嗡嗡嗡”聲音會使他們極為難受，尤其在夜間使人難以入眠。

圖8 不同時刻聲壓波動p′

圖9 聲壓級頻譜圖

圖10為聲場被完全解析后，在風力機軸心處3個垂直法向截面上SPL聲壓級的云圖，可以看出沿著下風向的聲壓級強度比上風向的聲壓級強度更大，風力機周圍的云圖不完全對稱，向下風向輕微偏移。

圖10 風力機周圍SPL聲壓級云圖

風力機周圍的聲壓級可以達到100 dB，但在向外擴散過程中衰減，風力機垂直于風向兩側的聲壓級云圖較弱，這與基于各種半經驗模型[26]畫出的聲壓級指向性圖特征相似。由于網格精度的限制，遠場的真實聲壓級會更強。致動線模型沒有考慮塔架的影響，在后面的研究中可以基于致動線相似的原理，將塔架簡化成固定的體積力加入控制方程，模擬塔架對聲場以及流場的作用，以提高精度。

圖11給出了風力機周圍半徑100 m和半徑240 m處的SPL指向性分析。

圖11 不同半徑處聲壓指向性圖

可以看出，由于采集點離風力機很近，噪聲還未開始進行對稱式擴散衰減，半徑100 m處的聲壓指向性圖分布相對均勻，這一點與圖10（c）一致；而到了半徑240 m處，聲場在擴散的過程中逐漸變得不均勻，但呈現對稱分布的特征，且在風力機兩側聲壓級收縮，在下風向位置聲壓級強度突出。240 m處聲壓級強度整體小于100 m處的聲壓級強度，但在局部由于地面反射作用聲壓強度更強，地面反射的作用在遠場會被弱化。

由于該風力機體型很大，難以開展相關的流場以及聲場實驗，缺乏實驗數據對照。但本文對該風力機進行仿真計算時，除了成熟的制動線模型外，采用的聲場計算方法在點聲源擴散模擬中已經得到驗證。

在以后的風場設計、城市小風力機等設計時，需要綜合考慮距離、方位的影響，結合噪聲類型、頻率對人的聽覺干擾，根據噪聲傳播特征布置合適的隔音板，建立綠色、清潔、舒適的生活工作環境。

3 結論與展望

首先模擬點聲源擴散，驗證了聲學擾動方程以及代碼編寫的正確性。聲場采用基于聲學波動方程的微分求解方法，與傳統的FW-H積分法相比，避免了在公式推導過程中的簡化誤差，同時能夠形象體現聲場傳播過程。

提出了一種新的模擬風力機噪聲的方法，結合致動線模型和BPM半經驗模型各自的優勢，共同為聲學擾動方程提供聲源，來計算風力機氣動噪聲。

研究了單個風力機在穩定均勻來流工況下的聲場情況，后面將會對多風力機、復雜地形以及湍流來流進行研究。