符號動力學信息熵參數優化方法研究

丁 闖，張兵志,2，馮輔周，吳守軍

（1.陸軍裝甲兵學院 車輛工程系，北京 100072； 2.北方特種車輛研究所，北京 100072）

符號動力學信息熵（Symbolic Dynamic Entropy，SDE）能夠有效檢測振動信號時間序列的動力學特性[1]，因此，SDE在特征提取及故障診斷中的應用越來越引起人們的重視。SDE具有計算速度快、對數據量要求小且能捕捉到時間序列的非平穩特性、能夠快速有效提取振動信號的運行狀態等特征。

然而，SDE的計算結果受自身參數的影響比較大，參數的選擇主要依靠人為經驗，限制了SDE的應用。本文將對參數確定的2種觀點進行闡述，對比了2種觀點中參數確定的典型方法，并通過對比優化參數，提高SDE作為特征的算法效率和敏感度。

1 SDE原理

SDE最早由Kurths等提出[2]，計算方法過程如下：

設振動信號序列X={x(i),i=1,2,…N}，即時域信號由N個采樣點元素組成。

（1）振動信號符號化。將時間序列X轉化到符號域S={s(i),i=1,2,…,N}，即s(i)代表符號域S中的第i個元素。符號域中符號使用si表示，其中，si∈{0,1,2,3}，此處si代表符號{0,1,2,3}的具體某個符號，具體轉化方法為

式中：μ為時間序列X的平均值，α為權重，一般取α=0.1[3]。

（2）相空間重構。對符號域的時間序列S=進行相空間重構，得到矩陣S0

其中：m為嵌入維數，τ為延遲時間，j=1,2,3,…,K，其中，K=N-(m-1)τ。重構矩陣中的每一行S0(j)為一個重構分量，重構矩陣中共有K個重構分量。

重構矩陣中每個重構分量為一個獨立的狀態模式，由于S0(j)有m個元素，每個元素的符號共有4種可能，因此共有n=4m種狀態模式。

（3）計算各狀態模式出現的概率。統計各狀態模式出現的次數，記為Z(l)(l=1,2,3,…,n)，并計算其出現的概率，記為

（4）計算符號動力學信息熵。

根據SDE原理，相空間重構是算法中的關鍵一步，其延遲時間和嵌入維數的選擇對SDE的計算結果有較大的影響。

2 SDE參數優化

相空間重構最早由Takens在1981年提出[4]，關于延遲時間τ和嵌入維數m的選擇，相關學者進行了大量的研究[5]。

目前對于參數選擇有兩種觀點：

(1)延遲時間和嵌入維數的選擇互不相關，即兩者獨立確定，通常使用互信息法和偽近鄰法相結合，首先使用互信息法確定延遲時間，然后在延遲時間確定后，使用偽近鄰法確定嵌入維數；

(2)延遲時間和嵌入維數的選擇存在聯系，即兩個參數的選擇相互依賴，通常使用關聯積分法（即CC算法），通過構造統計變量和延遲時間的關系確定最佳延遲時間和嵌入窗寬，根據嵌入窗寬確定嵌入維數。針對不同的應用需要根據其具體效果確定參數選擇的具體方法。

對于設備不同運行狀態下的時域振動信號，采用相同參數對其進行相空間重構，將得到不同的SDE。因此，可使用系統正常狀態下的振動信號確定的參數，對系統不同狀態下的振動信號進行SDE計算，將熵值作為特征用于判斷系統的運行狀態，從而達到特征提取的目的。

2.1 延遲時間和嵌入維數的獨立確定方法

（1）基于互信息法確定延遲時間

對于振動信號序列X={x(i),i=1,2,…M}，其符號域的時間序列S={s(i),1,2,…,N}，為了研究s(i)與s(i+τ)的相關性，選取延遲序列s(i+τ)構成新的序列Q={q(i),i=1,2,…M}，將S與Q的相關性大小作為確定延遲時間τ的依據。根據信息論理論，兩個時間序列的互信息可表示為

式中：Ps(si)和Pq(qi)分別為對應的符號域時間序列中事件si和qj的概率，Psq(si,qj)為事件si和qj的聯合分布概率，此處事件si和qj分別對應相應序列的各個符號。

對于某一特定符號域時間序列S，其與延遲后的時間序列Q的互信息值只與延遲時間有關，令

式中：I(τ)的大小代表了在已知時間序列S與時間延遲后時間序列Q的相關性。當I(τ)=0時，表示S和Q完全不相關；當I(τ)取極小值時，表示S和Q最大可能的不相關，重構過程中，使用I(τ)的第一個極小值對應的延遲時間τ作為最優延遲時間[6]，記為τ0。

（2）基于偽近鄰法確定嵌入維數

偽近鄰法（False Nearest Neighbor，FNN）是確定最小嵌入維數的一種有效方法，其計算過程為：若嵌入維數為m時的重構相空間的近鄰點仍然為嵌入維數為m+1的近鄰點，則此點為真近鄰點，反之若嵌入維數為m時的重構相空間的近鄰點不是嵌入維數為m+1的近鄰點，則此點為偽近鄰點。當嵌入維數處于某個值m時，偽近鄰點百分比（False Nearest Neighbor Percent，FNNP）將突變下降至0或接近0，且隨著m的增大不再變化，此突變點對應的m值即為所求嵌入維數，記為m0。

偽近鄰法確定嵌入維數的具體步驟如下：

當嵌入維度為m時，針對相空間中的任一重構分量S0(j)，在重構向量中，與S0(j)歐式距離最近的重構向量稱之為S0(j)的最近鄰點，記為SN0N(j)

此時，有

式中：j≠i，其與重構分量S0(j)的距離為

同理，求得嵌入維數為m+1時，其重構分量S0′(j)與其最近鄰點SN0,Nm+1(j)的距離為Dm+1(j)，此時可得

引入兩個偽近鄰點判據

式中：為符號域時間序列Q的均值，Rtol和Atol為選取的閾值。判據（1）通常用于有限長無噪聲的數據，判據（2）通常用于含噪聲的數據。

由此可知，重構矩陣中的K個重構分量對應K個最近鄰點，若K個最近鄰點有l個偽近鄰點，則此時偽近鄰百分比（即偽近鄰率）為

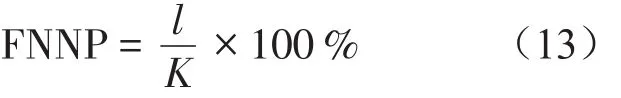
在實際計算過程中，將嵌入維數m從2開始依次增加，計算偽近鄰點百分比，直到偽近鄰點百分比小于5%或不再下降時，此時的嵌入維數即為最小嵌入維數[8]，記為m0。

2.2 延遲時間和嵌入維數的聯合確定方法

延遲時間和嵌入維數的聯合確定通常使用關聯積分法（C-C算法），該方法最早由Broomhead和Kim提出，是一種同時確定最佳延遲時間和最佳嵌入維數的算法。其基本思想是通過嵌入時間序列的關聯積分構造能夠代表非線性時間序列相關性的統計量，根據其和延遲時間的關系確定最佳延遲時間和嵌入窗寬，進而確定嵌入維數。C-C算法是根據大量的統計規律中得到的，具有一定的優勢。

對于時間序列X對應的符號域時間序列S={s(i),1,2,…,N}，其相空間中的重構分量為S0(j)，得出嵌入時間序列的關聯積分方程為

式中：K為相空間矩陣中重構向量的數量，即K=N-(m-1)τ；r為參考半徑，即為閾值；dij為重構向量中任一兩個重構分量S0(i)和S0(j)的距離，即dij=‖S0(i)-S0(j)‖ ；H(u)為Heaviside函數，其取值為

對于任意的參考半徑r，C(m,τ,N,r)代表任意兩個重構分量的距離小于r的個數占總數的C2K中的比例。對于符號域時間序列S，首先將時間序列進行劃分，分成τ個長度相等的時間序列，τ為延遲時間。然后構造一個與延遲時間τ相關的關聯方程：

當延遲時間τ=1時為單個時間序列本身，而此時，有

當延遲時間τ=2時，有2個時間序列，為和{s(2),s(4),…,s(N)} ，長度為，而此時，有

以此類推，可得出當延遲時間τ為任意自然數時，其關聯方程為F(m,τ,N,r)。

當N→∞時，則

由上式可知，當時間序列中的點為獨立分布且N→∞時，所有的F(m,τ,r)均為零。然而實際序列的長度為有限值，且時間序列中的點是相關的，因此F(m,τ,r)并不是總為零。若參考半徑r為任意值、F(m,τ,r)均為極小值點時，時間序列最接近均勻分布。此處，將F(m,τ,r)的最大值和最小值的差定義為

在求解過程中，Brock等通過對各種分布的研究，得出結論：當時間序列的長度N≥500時，對于嵌入維數m，一般取2≤m≤5，對于參考半徑r，一般取為時間序列的標準差），可得到較好的結果。而將其應用于符號動力學信息熵特征提取時，若嵌入維數取2，得出的信息熵難以區分故障模式，因此，在計算時，可取1,2,3,4。然后構造以下3個統計量

3 試驗驗證

為了檢驗并對比參數優化方法的有效性，在SDE取不同參數條件下對行星齒輪箱振動信號進行特征提取。行星齒輪箱試驗臺如圖1所示。

圖1 行星齒輪箱試驗臺

試驗臺主要由變頻電動機、行星齒輪箱、渦流測功機組成，變頻電動機提供動力，由渦流測功機加載，行星齒輪箱的參數如表1所示。

表1 行星齒輪箱參數

分別對行星齒輪箱齒輪正常、太陽輪輪齒局部裂紋故障、行星輪輪齒局部裂紋故障等3種狀態信號進行分析[7-9]。

此試驗中2種狀態的振動信號均在有負載情況下完成，其中，變頻電機輸入轉速為2400 r/min，采樣頻率為5120 Hz。正常信號、太陽輪裂紋故障、行星輪裂紋故障時域波形如圖2所示。

圖23 種狀態振動信號的時域波形

（1）SDE信息熵參數確定

首先利用互信息法計算正常狀態下振動信號符號域時間序列的延遲時間τ與互信息之間的關系，如圖3所示。

圖3 振動仿真信號互信息與延遲時間的關系

由圖3可知，互信息第一次取得極小值時，最佳延遲時間τ0=8。

當輸入延遲時間τ0=8時，使用偽近鄰法求解時間序列的嵌入維數，使用判據（2），選擇閾值Atol=2，求出此時間序列的偽近鄰率與嵌入維數的關系如圖4所示，由圖4可知，最佳嵌入維數m0=3。

使用聯合積分法即C-C方法確定延遲時間和嵌入維數，圖5為由聯合積分法得出的相關參數變化曲線。

由圖5可知，當圖中)變化曲線取第1個零點或接近零點時，τ0=20，且Fcor(τ)變化曲線取最小值時，最佳嵌入窗寬τw=25，此時根據式（21）可得，m=3；當圖中(τ)變化曲線取第一個極小值時，τ0=35，同理得m=2。由前文可知，嵌入維數至少大于2，因此，得出最佳延遲時間τ0=20，最佳嵌入維數m0=3。

圖4 振動仿真信號偽近鄰率與嵌入維數的關系

圖5 聯合積分法各參數的變化曲線

（2）特征提取

取齒輪正常、太陽輪裂紋故障、行星輪裂紋故障各20個樣本，使用SDE計算3種狀態下各個樣本的熵值。使用獨立方法和聯合積分法確定參數的各狀態下SDE如圖6、圖7所示。

圖6 根據獨立確定方法確定參數的各狀態SDE

圖7 根據聯合積分法確定參數的各狀態SDE

為進一步突出本文2種方法確定參數的實際應用效果，在實際計算中，增加任意選定的參數計算，任意選定延遲時間τ0=4，嵌入維數m0=3，此參數下各狀態下SDE如圖8所示。

圖8 任意給定參數的各狀態SDE

由圖6、圖7、圖8可知，使用獨立方法確定的參數計算得到的3種狀態下的SDE值相差最大，即分類效果最好，且同種狀態下的SDE較穩定。因此使用互信息法確定延遲時間，根據偽近鄰法確定嵌入維數，具有更好的分類效果。

4 結語

本文重點研究符號動力學信息熵參數優化確定方法。根據其算法原理，使用相空間重構的方法確定算法參數，克服了人為主觀或憑經驗確定算法參數的不確定性。根據當前確定相空間參數的兩種不同觀點，介紹了2種方法中典型參數確定方法的基本原理，并利用行星齒輪箱實測信號對所提參數優化方法進行了驗證。結果表明，相空間重構參數的獨立確定方法比聯合確定方法更優，這為符號動力學信息熵算法中參數的確定奠定了基礎。