基于磁流變阻尼器的6自由度半主動隔振系統

廖 勇，朱 煒，江 民，芮筱亭

（南京理工大學 發射動力學研究所，南京 210094）

直升機的振動水平和噪聲水平會影響其隱身性和機組成員的舒適性，是現代軍用直升機的一項重要戰術技術指標，影響直升機的作戰效能和戰場生存能力。處于非對稱、非定常的氣動環境中的直升機旋翼成為了直升機的主要振源。旋翼各葉片上產生的激振力傳遞到槳根處合成激振力和力矩，通過主減速器傳遞到機身及其他部件，因此在主減速器和機身之間安裝隔振裝置可以有效減小直升機的振動[1-2]。

Stewart機構作為典型的并聯機構，具有承載能力強、精度高、結構穩定緊湊、運動慣量小、動態特性好等優點[3]，國內外學者對其進行了許多研究。Stewart機構的動力學建模方法除了常規的拉格朗日法和牛頓-歐拉法外，也有學者提出了一些新的方法，比如G Chen，X Rui[4]等使用多體系統傳遞矩陣法建立Stewart機構的線性動力學模型，該方法的特點在于計算速度快。錢承[5]等分析了Stewart并聯機構的動力學特性，并通過Adams仿真，模擬了Stewart并聯機構的工作狀況和振動特性。磁流變阻尼器則可以通過控制輸入的電流改變其阻尼力的大小，是近年來半主動隔振的主要耗能器件之一，其具有出力大且可控、結構簡單、具有失效安全性等優良特點[6]。因此，基于Stewart機構的6自由度磁流變半主動隔振平臺將具有承載能力強、可減小6個自由度方向的振動、隔振帶寬大等優良特點。Memet Unsal[7]建立基于磁流變阻尼器的6自由度半主動懸架模型并進行了理論仿真，結果表明其設計的隔振平臺在X、Y、Z3個平移方向的減振效果良好。王強[8]設計了一個立方體構型的6自由度磁流變隔振平臺，仿真和實驗的結果表明平臺可以有效抑制共振，并在高頻區也有良好的減振效果。Jean等[9]設計了一個用于衛星整星微振動隔振的平臺，該平臺基于Stewart機構，采用磁流變阻尼器作為耗能元件，他們的實驗表明該隔振平臺效果甚好。

直升機主減-旋翼系統的振動一般在12 Hz～25 Hz，屬于低頻隔振。傳統的主減隔振方式主要有節點梁隔振、聚焦式隔振以及動力反共振隔振，他們都屬于被動隔振，只對特定頻率有較好的隔振效果，隔振帶寬小[11-13]。為解決傳統主減隔振的這些缺點，設計了一個采用磁流變阻尼器的基于Stewart機構的主減安裝隔振系統，該系統由一個支腿是磁流變阻尼器的六自由度的平臺及其半主動控制系統組成。首先使用牛頓-歐拉法建立6自由度隔振平臺的動力學模型，分析其動力學行為；其次通過磁流變阻尼器的力學性能實驗，建立磁流變阻尼器的動力學模型；最后，通過計算機數值仿真，驗證控制方法并分析所設計隔振平臺的隔振性能。

1 6自由度隔振平臺動力學建模

采用牛頓-歐拉法建立基于Stewart機構的6自由度隔振平臺的動力學模型。隔振平臺模型如圖1所示。

平臺由一個上平臺（直徑小）、一個下平臺（直徑大）和6根支腿組成。在下平臺建立慣性坐標系Odxdydzd，支腿與下平臺連接點分別為d1、d2、d3、d4、d5、d6；在上平臺幾何中心處建立連體坐標系Ouxuyuzu，支腿與上平臺連接點分別為u1、u2、u3、u4、u5、u5。

連體系中一點P轉換到慣性系中的坐標為

式中，R表示連體系轉換到慣性系的旋轉矩陣；上標d和u表示點所在坐標系，若無，則默認為慣性系表示連體系原點在慣性系下的位置矢量。

1.1 支腿運動學分析

第i條支腿所在直線的矢量

式中：ru,i和rd,i分別表示上下平臺與支腿連接點在慣性系中的位置矢量，該式即為隔振平臺的運動反解方程。

第i條支腿單位矢量

式中：Li為第i條支腿長度

將式(2)兩邊對時間t求導，即可得到平臺與第i條支腿連接點的速度與上平臺速度關系為

式中：ω為上平臺和負載旋轉角速度。

n˙i可以分解為沿支腿矢量方向的速度和垂直于支腿方向的速度，設W為支腿旋轉的角位移，則

在式(5)兩邊叉乘ei化簡可得到支腿旋轉角速度為

圖1 平臺簡化模型

將式(4)對時間t求導，可以得到支腿連接點加速度與平臺姿態的關系

同樣，連接點的加速度可以分解成沿支腿矢量方向的分量和垂直于支腿矢量旋轉的角加速度，即將式(5)對時間求導，得到

在等式兩邊點乘ei，整理可得到沿支腿方向的加速度為

在式(9)兩邊叉乘ei，整理可以得到支腿旋轉的角加速度為

1.2 支腿動力學分析

考慮整條腿上的力矩平衡，并忽略球鉸和虎克鉸的摩擦力，可得到腿的歐拉方程

式中：mldrld×ald為支腿下部分加速度引起的力矩；mlurlu×alu為支腿上部分加速度引起的力矩；(Ild+為支腿轉動引起的力矩；n×Fs為支腿與上平臺接觸點的約束力矩；Mlue為支腿下部虎克鉸的約束力矩。

令

則式(11)可以寫為

式(12)兩邊叉乘ei以消去未知量Mlu，整理得到

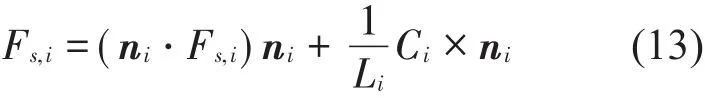
式(13)表示支腿對上平臺的作用力。

支腿上部分的力平衡方程為

式中：Fi是第i條支腿阻尼器和彈簧的合力。

將式(13)代入式(14)中，整理得到

式(15)即為阻尼器需要輸入的力

1.3 平臺動力學分析

上平臺的牛頓平衡方程為

式中：a是上平臺和負載重心的加速度；M是上平臺和負載的質量；Fw是施加在負載和上平臺上的外力。

將式(13)代入式(16)得到

根據平臺的重心處力矩平衡，列出歐拉方程為

式中：r為負載和上平臺重心點到隔振平臺重心點的位置矢量；Mw為施加在上平臺和負載的外力矩。

式(17)和式(18)給出了 6個方程，包含了x1、x2、x3、x4、x5、x66個未知數。將式(17)和式(18)聯立，寫成矩陣形式得到

式中：

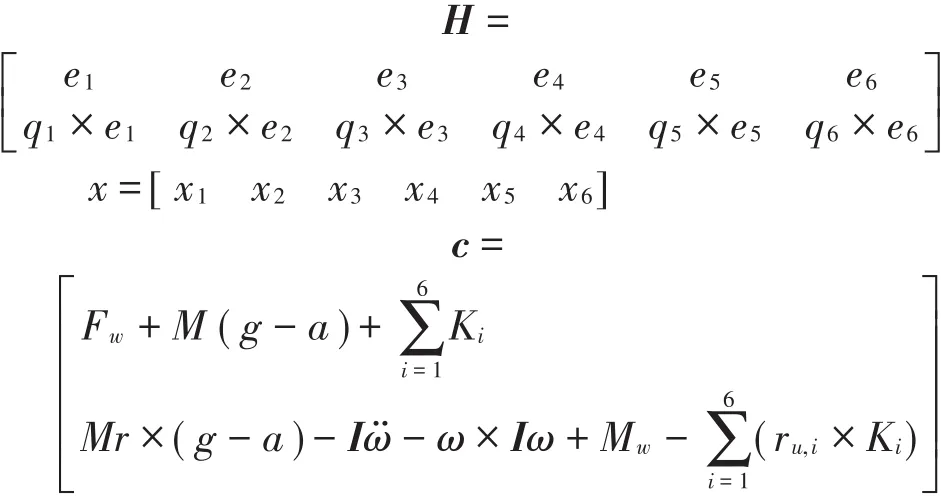
對于式(19)表示的線性系統，可以求解出x，即ni·Fs,i，再由式(15)即可求得需要阻尼器和彈簧提供的力。

2 磁流變阻尼器建模

磁流變阻尼器通常由活塞、活塞桿、氣囊、勵磁線圈以及磁流變液組成，如圖2所示。

圖2 磁流變阻尼器結構

當勵磁線圈通電產生磁場，磁流變液通過有磁場的阻尼通道時，黏度變大。通過改變電流大小來控制磁場強弱，可以控制磁流變液的黏度，進而達到控制阻尼力大小的目的。

2.1 阻尼器力學性能測試

采用Lord公司生產的阻尼器作為磁流變阻尼器的樣機阻尼器，阻尼器如圖3所示。

圖3 Lord RD-8040-1磁流變阻尼器

其參數如表1所示。要使阻尼器能夠正常工作，需要對其進行力學性能測試。

測試工具為W+B動態疲勞實驗機，測試系統如圖4所示。

通過測試得到磁流變阻尼器在不同工況下的力-位移曲線和力-速度曲線，圖5和圖6分別是激勵為10 mm、1 Hz和10 mm、2 Hz在不同電流工況下的力-位移曲線和速度-位移曲線。

從圖中可以看出，阻尼器的示工曲線飽滿，阻尼器最大出力達到1.5 kN，而最小出力僅100 N，阻尼可調系數（庫侖力與黏滯阻尼力的比值）將近15，阻尼可調范圍極大，阻尼器的動力學性能優秀。

2.2 建立阻尼器力學模型

使用Bouc-Wen模型來模擬磁流變阻尼器的動力學行為。Bouc-Wen模型曲線連續光滑，能夠很好地模擬出在低速情況下的阻尼力-速度曲線，尤其能夠反映低速情況下的滯回特性。該模型如圖7所示。

圖4 阻尼器力學性能測試系統

阻尼力表達式為

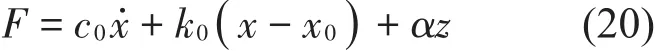
其中：滯變位移z由式(21)給出

式中：F為磁流變阻尼器總阻尼力；c0為磁流變液屈服后黏性系數；a為滯變力與磁流變阻尼器總阻尼力所占比例的調節參數；Z為滯變位移；x為阻尼器的位移；x˙為阻尼器的速度；A為與最大阻尼力相關的比例系數；β為與滯回環高度相關的調節參數；n為曲線圓滑系數，一般取n=2；γ為與滯回環寬度相關的調節參數；k0為塑性階段阻尼器滯回環寬度的調節參數。

通過調整模型參數γ、β和A的取值，可以改善模型輸出的力-速度回程曲線的線性形狀和屈服前后漸變段的光滑性。

圖510 mm、1 Hz工況下的力-位移曲線和速度-位移曲線

Bouc-Wen模型的參數需要根據實驗數據，通過參數識別獲取。本文采用遺傳算法進行參數識別。遺傳算法的基本步驟包括：編碼、初始群體的生成、交換、適應度值的評估檢測、優良個體選擇、變異、終止等。

圖610 mm、2 Hz工況下的力-位移曲線和速度-位移曲線

圖7 Bouc-Wen模型

Bouc-Wen模型中有α、c0、k0、γ、β、A、x0等7個參數需要進行識別。從實驗圖看來，磁流變阻尼器的滯回曲線不存在偏移現象，所以可以取x0=0。取擬合值與實驗值的均方根誤差作為目標函數，即

式中：i為第i個采樣點，F為擬合的阻尼器力輸出值，Ft為實驗阻尼器力輸出值。

通過采用逐步縮小參數范圍的方法以提高精度，遺傳算法的參數選取如表2所示。除表中所列參數，其余參數均采用遺傳算法工具箱的默認值。

Bouc-Wen參數擬合結果為

表2 遺傳算法參數

式中，I為磁流變阻尼器的輸入電流。

選取部分工況下的數據進行擬合，驗證Bouc-Wen模型可靠性。圖8是對激勵為10 mm、2 Hz、電流為0 A、0.5 A、1 A、1.5 A、2 A的工況下，阻尼器的實驗數據與擬合數據的對比圖。

從圖中可以看出，擬合出的曲線與實驗的曲線重合度很高，表明本次識別的磁流變阻尼器的Bouc-Wen模型可以真實反映出磁流變阻尼器實際的力學行為。

圖8 擬合曲線與實驗曲線對比圖

3 隔振系統仿真

3.1 on-off控制

理想的天棚控制是設想將阻尼器安裝在負載和虛擬的慣性空間（sky）之間，如圖9（a）所示。理想天棚控制的阻尼力為

式中：csky為天棚阻尼器阻尼系數。

天棚阻尼控制的特點是阻尼器只產生與負載運動方向相反的阻尼力Fd，可以有效抑制負載的運動。但在實際工程中，難以將阻尼器安裝在負載與“天棚”之間。

Karnopp等提出了on-off控制來近似實現理想的天棚阻尼控制。其原理是將阻尼器安裝在負載與基底之間，如圖9（b）所示。

圖9 理想天棚阻尼控制與等效天棚阻尼器控制

定義vm負載質量的速度，向上為正；vx為負載與基底的相對速度，其為正時，基底與負載距離增大。與理想天棚阻尼控制相比，on-off控制有以下兩種情況:當vm·vx＞ 0時，on-off控制和理想天棚阻尼控制所產生的阻尼力方向相同，兩者的作用相同；當vm·vx＜0時，on-off控制和理想天棚阻尼控制所產生的阻尼力方向相反，兩者的作用相反，on-off控制會惡化隔振效果，需要使阻尼器出力最小。

綜上，on-off控制策略可以描述為on-off控制與理想天棚控制作用相同時，給磁流變阻尼器輸入最大電流；作用相反時，斷開磁流變阻尼器的供電。即

式中：Fd(Imax)和Fd(Imin)分別表示輸入最大電流和最小電流時磁流變阻尼器輸出的力。

3.1 單腿仿真

首先，使如圖9（b）所示的簡單模型，即單腿模型，驗證on-off控制策略的有效性。

使用Solidworks與SimMechanics聯合仿真來搭建單腿的數值仿真模型，如圖10所示。

圖11是阻尼器與彈簧模塊，需要向其輸入腿的相對位移、負載絕對速度、腿的相對速度，其輸出是圖10中的Fd，仿真參數如表3所示，結果見圖12。

圖10 單腿模型

表3 單腿隔振系統仿真參數

圖11 磁流變液阻尼器與彈簧模型

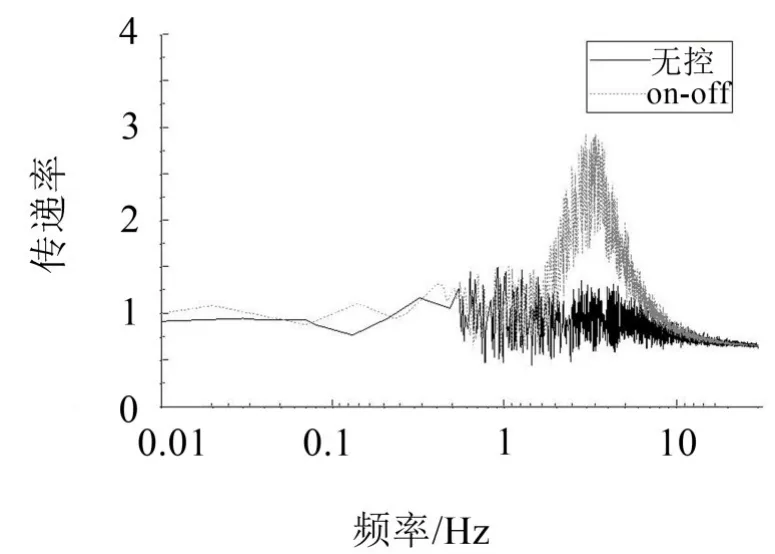
圖12 單腿有控制與無控制振動傳遞率

3.26 自由度隔振系統仿真

同樣，6自由度磁流變阻尼器半主動隔振系統的性能仿真采用Solidworks與SimMechanics聯合仿真。在Solidworks中繪制如圖13所示的隔振平臺的三維圖形后，根據前文推導的6自由度隔振平臺的動力學方程，在SimMechanics中搭建出如圖14所示的隔振系統動力學仿真模型。隔振系統的仿真參數見表4。該模型的重力方向為-Y方向。

圖13 隔振平臺三維圖

表4 隔振系統仿真參數

彈簧與磁流變液阻尼器的系統輸入是支腿與上下虎克鉸鏈接的點的相對速度和相對位移、負載的絕對速度，輸出加載在上下虎克鉸之間的力Fd。

在Y軸方向施加加速度正弦掃頻激勵信號，振幅為1 g，頻率為0.1 Hz～30 Hz。無控和有控的仿真結果如圖15所示。

從圖15可以看出平臺共振區為3 Hz～5 Hz，有控制的隔振平臺隔振性能優秀，在有效降低共振的同時，在10 Hz～30 Hz的高頻段有50%以上的隔振效果。

同樣在Z軸施加一個加速度正弦掃頻激勵信號，幅值為0.1 g，頻率范圍為0.1 Hz～30 Hz，無控和有控的仿真結果如圖16所示。

從圖16可以看出平臺共振區在0.6 Hz～0.9 Hz，有控制的隔振平臺隔振性能優秀，有效降低共振的同時，在10 Hz～30 Hz的高頻段有40%以上的隔振效果。由于6自由度隔振平臺具有對稱性，因此平臺在Z軸和X軸方向上的振動效果是一樣的，因此在此不再贅述X軸方向的掃頻振動。

圖146 自由度隔振系統仿真模型

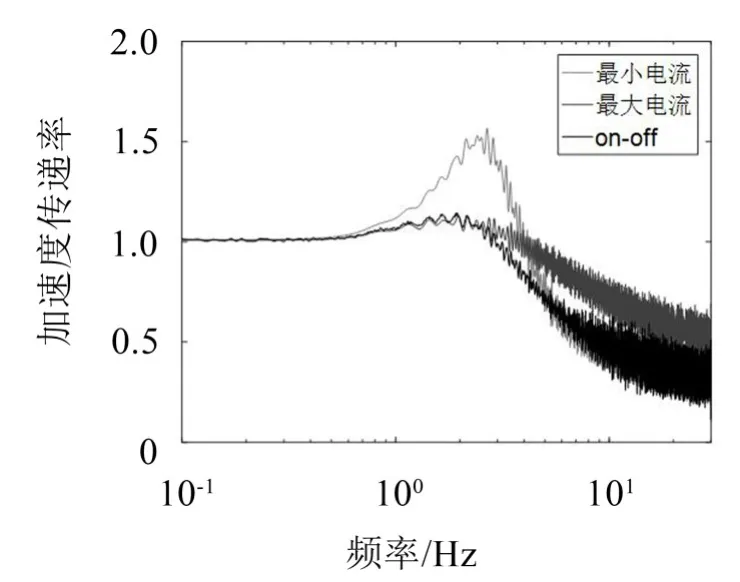
圖15 Y方向加速度掃頻激勵下的振動傳遞率

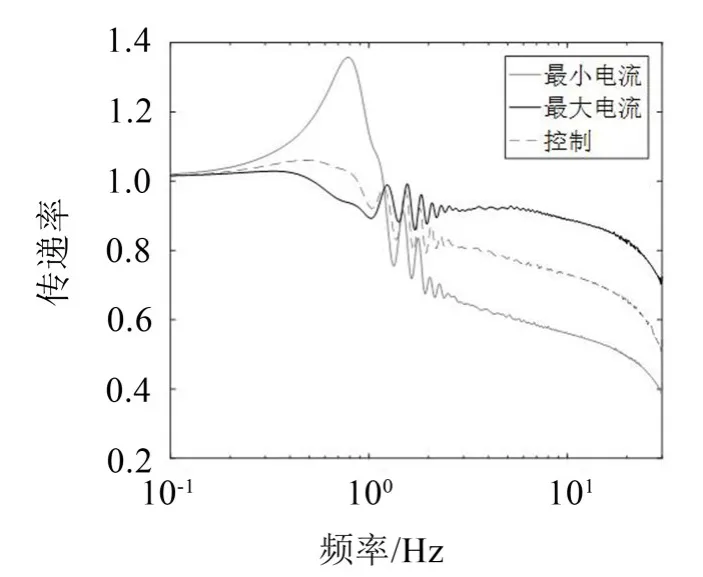
圖16 Z方向加速度掃頻激勵下的振動傳遞率

由于Stewart機構具有強耦合性，因此為了進一步了解隔振平臺的性能，給隔振平臺的下平臺同時施加X、Y、Z3個方向各自共振頻率的位移激勵，激勵如下

圖17 被動與on-off控制下支腿阻尼器的出力

圖18 未施加控制與on-off控制下支腿伸縮量

從仿真結果看，各支腿磁流變阻尼器出力和伸縮量均在阻尼器的標定范圍內。對比圖17和圖18中未施加控制和施加控制后腿的出力和伸縮量可以看出，on-off最優控制是有效果的，施加控制后，阻尼器的出力和伸縮量都有一個明顯的跳躍變化，與式(23)的描述相一致。

在無旋轉激勵的情況下，隔振平臺產生了繞X軸和Z軸的角位移，而基本無繞Y軸的轉動，這表明隔振平臺具有一定的耦合性。表5列出了各方向上振動的均方根值。

表5 各方向的位移/角位移均方根

圖19 負載在X、Y、Z方向上的位移

從表5中可以清楚看出在施加控制后，耦合強度減弱，與被動相比，振動幅度都有減小。在X、Y、Z方向的平移以及繞X軸、繞Z軸轉動的共振頻率上，振動分別降低26.92%、39.46%、22.77%、53.06、56.79。仿真結果見圖19至圖20。

圖20 負載繞X軸、Z軸的角位移

4 結語

(1)本文針對直升機旋翼-主減系統多自由度振動問題設計了一個基于磁流變阻尼器的6自由度磁流變半主動隔振系統，采用牛頓-歐拉方法建立其動力學模型。

(2)通過磁流變阻尼器的力學性能實驗，得到磁流變阻尼器的力學性能。使用遺傳算法根據實驗結果識別出了磁流變阻尼器Bouc-Wen模型的參數，該模型可以較好反映出所使用磁流變阻尼器的實際動力學行為。

(3)隔振系統的仿真結果表明，該隔振系統具有較好的隔振效果，當激勵頻率高于共振頻率時，隔振效果良好，減少振動50%以上，可以有效降低直升機機體振動。