新奧法小凈距隧道拱頂沉降回歸分析研究

李忠文，易萍華，張廣武，朱蓮靚

（1東華理工大學 土木與建筑工程學院，江西南昌 330013；2上海電機學院 商學院，上海 201306）

0 引言

目前大多數隧道采用新奧法施工，隧道施工中圍巖變形是一個復雜的非線性過程，對其進行準確預測與評估具有重要的工程意義[1]。隨著非線性理論的不斷發展，圍巖變形的預測方法不斷增多。Mohammadi,S.D.[2]通過半經驗法、線性和非線性多元回歸分析法并結合編程技術對監測數據進行了分析，并建立多種模型來預測采用新奧法施工的隧道的最大沉降量。汪宏[3]采用ADINA有限元軟件建立三維有限元數值分析模型，模擬開挖后隧道圍巖的穩定性，并利用強度折減法對開挖后隧道的破壞情況進行了分析，提出了應對措施。

本文基于實際的隧道工程，對處于斷層破碎帶處的隧道圍巖變形運用回歸分析法，判斷圍巖穩定情況并預測出隧道二襯施作的合理時間，可以為其它相關隧道工程提供借鑒參考。

1 工程概況與監測

1.1 工程概況

該隧道位于浙江省境內，為小凈距短隧道，左線起訖樁號ZK41+615—ZK41+940，長325m，最大埋深約74.9m；右線起訖樁號K41+593—K41+942，長349m，最大埋深約65.4m，為雙洞雙向行車越嶺公路隧道。隧址區屬構造剝蝕丘陵地貌區，地形起伏較大。隧道范圍內中線高程為84.1～155.8m，山體自然坡度25°～45°，地表植被發育。

隧道進、出口段位于斜坡溝谷地帶，均為淺埋段。圍巖為強、中風化熔結凝灰巖，節理裂隙較為發育，巖體破碎，圍巖自穩能力較差。隧道洞身ZK41+755—ZK41+805、K41+745—K41+795段發育有全新世非活動斷層，斷層破碎帶寬約10m，走向與隧道軸線近乎垂直，且巖體極其破碎。圍巖為中風化熔結凝灰巖，圍巖類別為V級，自穩能力較差。

1.2 施工與監測方法

該隧道單洞采用交叉中隔墻法施工，在施工過程中充分利用圍巖自身的承載能力，使圍巖與支護結構共同形成支撐環。

根據隧道現場施工的具體情況以及隧道圍巖等級，測點埋設距離工作面1.5m，V級圍巖監測斷面間距為20m，開挖后12h內讀取初值，在下一循環開挖前，完成初期變形值的讀數。拱頂沉降量測頻率見表1。

表1 拱頂沉降量測頻率（按位移速度）

1.3 監測斷面

本文選取處于斷層破碎帶上隧道左洞ZK41+770斷面作為分析斷面，該斷面共設置有G1、G2、G33個測點，測點位置如圖1所示。其中G3測點監測的累計沉降量最大，最易發生圍巖失穩坍塌的情況，故提取該測點的監測數據進行回歸分析。

圖1 監測點布置示意

2 回歸分析

2.1 數據處理

在該隧道拱頂沉降回歸分析中，選擇監測時間作為自變量，累計沉降量作為因變量。

回歸分析對異常值非常敏感，異常值的存在會嚴重影響回歸分析的質量，最終影響預測值，而實際的監測數據往往會受到施工環境、測量誤差等因素的影響而出現較大的波動起伏，同時所監測的數據常存在非等間隔問題。因此在回歸分析前，為提高模型的精度，需對數據進行預處理。

對于異常點（xi，yi）往往采取鄰點中值法[4]進行剔除，取其兩側相鄰點的數據（xi-1,yi-1）和（xi+1,yi+1）的中點作為新的離散數據。新的離散點（xi,yi）計算公式為：

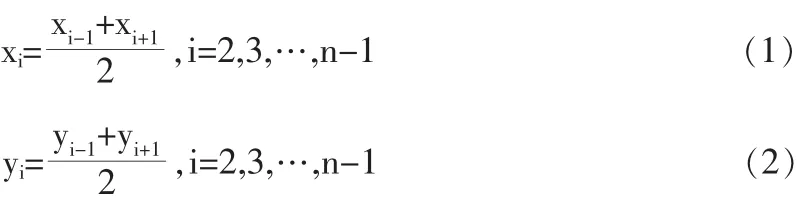
利用拉格朗日插值法對數據進行等間隔處理。取相鄰兩個離散點（xi-1,yi-1）和（xi+1,yi+1），新的離散點（xi,yi）計算公式為：

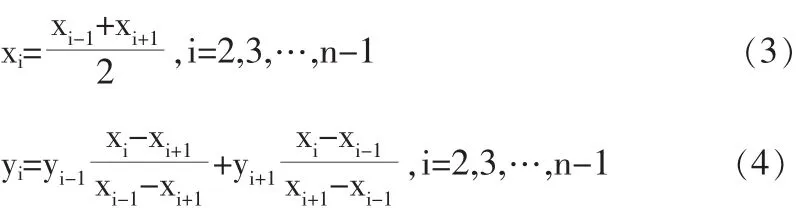
經過預處理后的數據如表2所示。

表2 ZK41+770斷面G3測點拱頂沉降實測值

2.2 數學模型建立

根據監測時間與累計沉降量之間的關系以及JTGF60-2009《公路隧道施工技術規范》的相關要求，初步確定使用一元非線性函數回歸分析法[5]，建立如下回歸模型：

式中：ε為隨機誤差。

對于一元非線性函數，可以通過變量替換，將其轉化為一元線性函數Y=a+bX，再利用最小二乘估計法，使每一個離散點（xi,yi）與f（xi）在該點處誤差的平方和達到最小來計算參數a、b和相關系數R。 a、b、R分別按公式（6）、（7）、（8）計算得到：

結合實測數據散點圖的特點，確定選用以下4個數學模型：

（1）冪函數模型：

（2）對數函數模型：

（3）雙曲線函數模型：

（4）指數函數模型：

式中：U為斷面拱頂沉降的累計沉降量；t為時間。

計算出各函數模型的相關系數R2，并選擇相關系數R2最大的模型作為預測的最相關模型。

3 回歸分析函數模型的確定

隧道左洞ZK41+770斷面布設時間為2018年6月2日，停測時間為2018年7月4日。結合前20天的監測數據，利用上述4種回歸模型，對左洞ZK41+770斷面G3測點進行回歸分析。

對于冪函數模型結合公式（6）、（7）、（8）、（9）進行計算，得到A=4.81249，B=0.28305，相關系數R2=0.96347。

對于對數函數模型結合公式 （6）、（7）、（8）、（10） 進行計算，得到A=2.31273，B=4.06445，相關系數R2=0.98156。

對于雙曲線函數模型結合公式（6）、（7）、（8）、（11）進行計算，得到A=-7.68489，B=10.34241，相關系數R2=0.81954。

對于指數函數模型結合公式 （6）、（7）、（8）、（12） 進行計算，得到A=11.09476，B=1.40043，相關系數R2=0.92043。

整理所得計算結果，可得ZK41+770斷面G3測點拱頂沉降回歸分析結果對比表，見表3。

表3 拱頂沉降回歸分析結果對比

各函數模型所對應的拱頂累計沉降量-時間變化規律，如圖2—圖5所示。

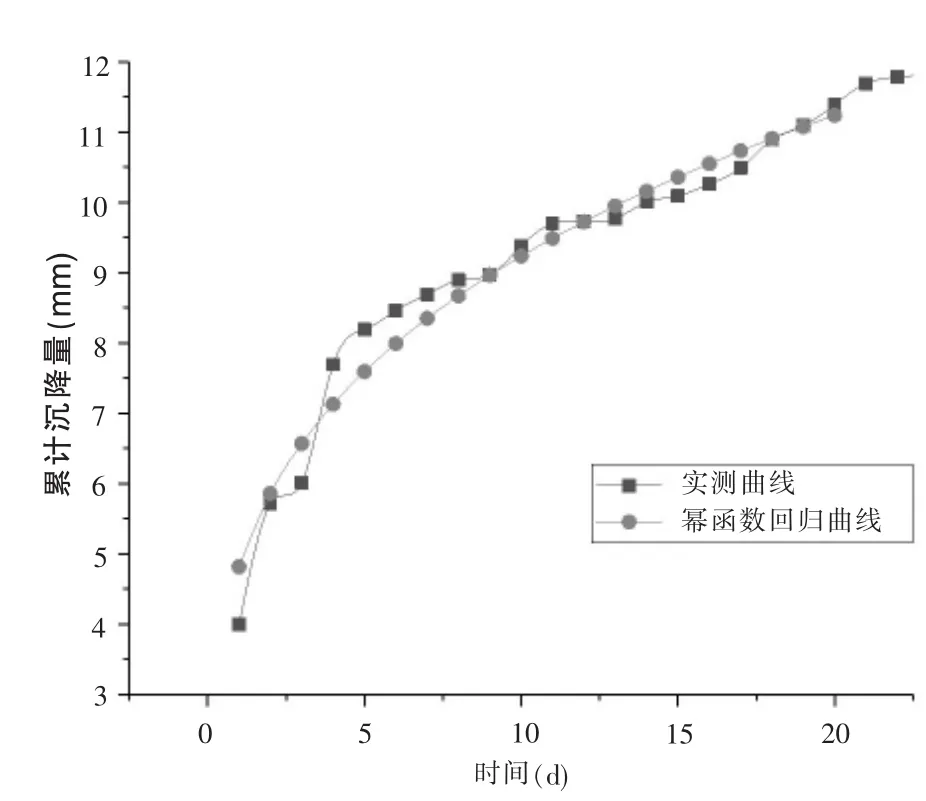
圖2 冪函數回歸曲線

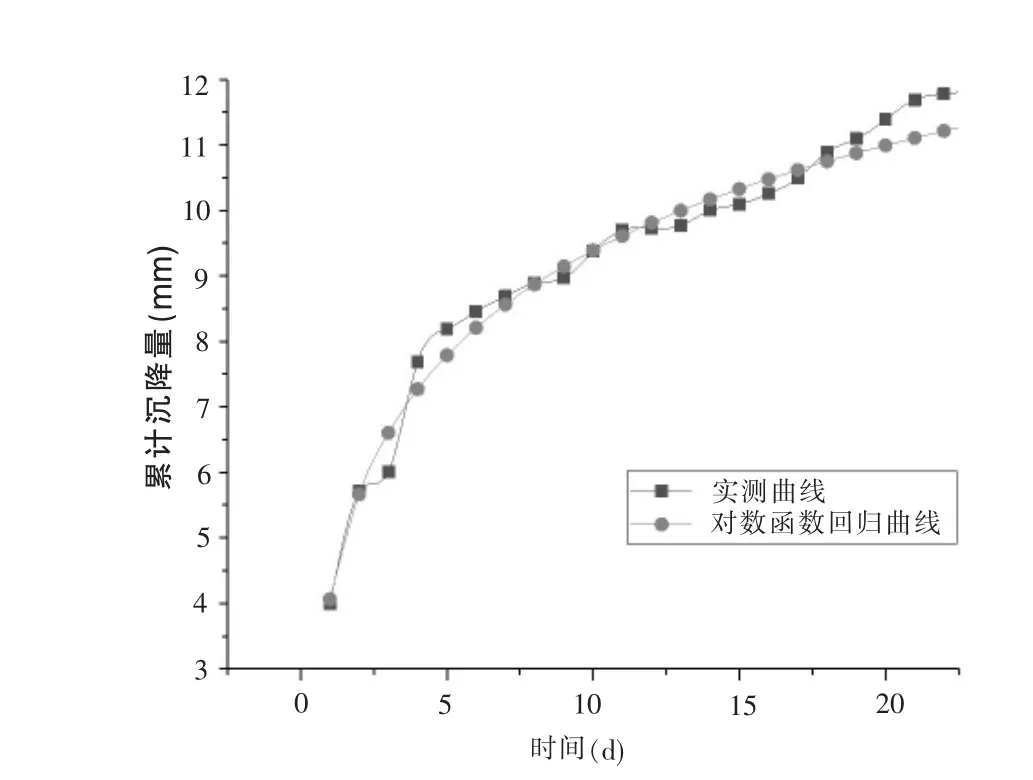
圖3 對數函數回歸曲線

圖4 雙曲線函數回歸曲線

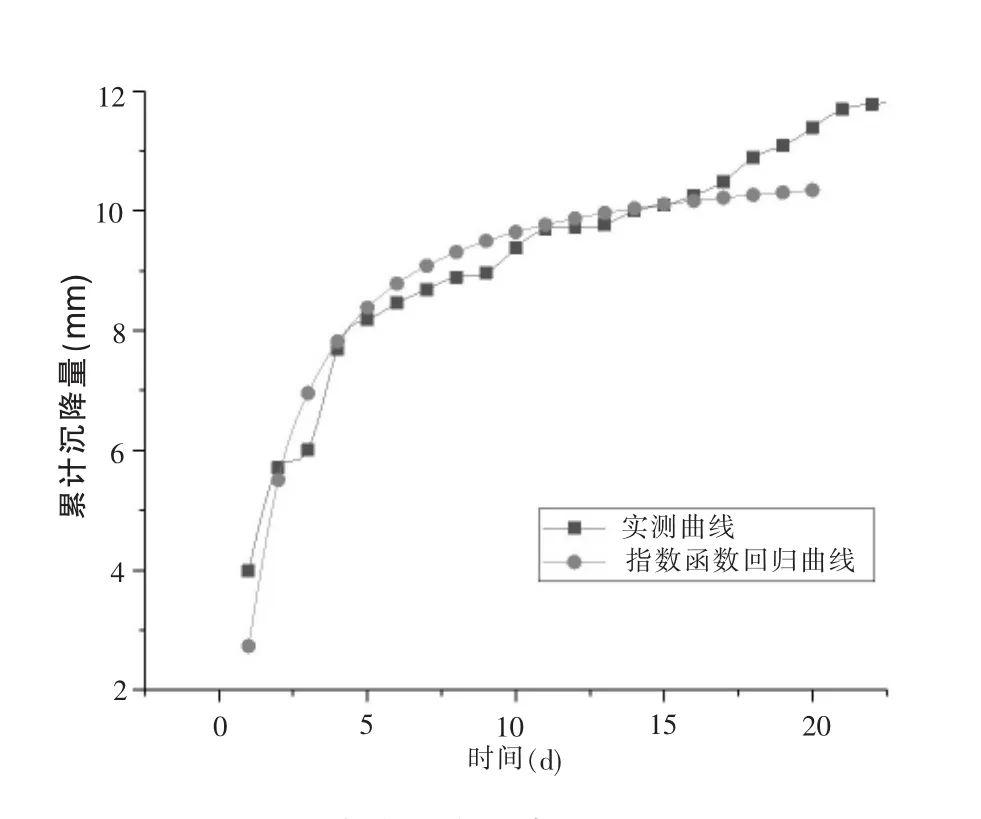
圖5 指數函數回歸曲線

4 實測對比驗證

在用于實際的預測之前往往需要對已建立的對數函數模型進行檢驗[7]。將t=21、22、……、32代入到對數函數模型U=2.31273lnt+4.06445中，計算出對應的拱頂沉降的分析值，并與實測值進行比較，可得到實測數據與分析值對比表，見表4。

為了更加直觀了解擬合效果，結合表2和表4可以做出圖6所示拱頂累積沉降量-時間擬合曲線圖。

定義回歸分析相對偏差率=（分析值-實測值）/實測值，經計算，通過對數函數模型所得分析值與實測值差距不大，穩定在-4.96%～1.51%之間，可以得出對數函數U=2.31273lnt+4.06445與實測結果相關性較好，可以用于隧道拱頂沉降量的預測。

根據大量隧道工程實踐經驗，對于拱頂的穩定性往往從兩個方面進行綜合判斷。（1）根據沉降速率判斷：根據現場的實際情況，拱頂沉降速率大于1mm/d時，拱頂處于急劇變形狀態；拱頂沉降速率在 0.1～1.0mm/d時，拱頂處于緩慢變形狀態；拱頂沉降速率小于0.1mm/d時，認為拱頂達到基本穩定；（2）根據沉降速率變化趨勢判斷：當拱頂沉降速率不斷下降時，拱頂處于穩定狀態；當拱頂沉降速率保持不變時，拱頂尚不穩定；當拱頂沉降速率不斷上升時，拱頂處于危險狀態。根據圖6可知，處于斷層破碎帶上ZK41+770斷面G3點拱頂沉降共經歷了從急劇變形、緩慢變形到基本穩定三個階段。從監測開始到第5天，拱頂沉降速率較大，這期間沉降量約占整個監測期間總沉降量的68.8%。對對數函數U=2.31273lnt+4.06445求一階導得拱頂沉降速率函，可以畫出圖7所示拱頂沉降速率實測曲線與函數曲線對比圖，從圖中可以看出拱頂沉降速率不斷下降，說明拱頂正趨于穩定。根據拱頂穩定性判斷依據函數預測，從第24天起拱頂趨于穩定，實測數據顯示從第22天起拱頂沉降速率小于0.1mm/d，拱頂趨于穩定，實測結果與預測結果相差不大，相互驗證。以該對數函數模型為基礎預測該隧道二次襯砌合理施作時間，應為監測開始后的第24天左右，可以以此為依據提前做好相應的施工準備工作。

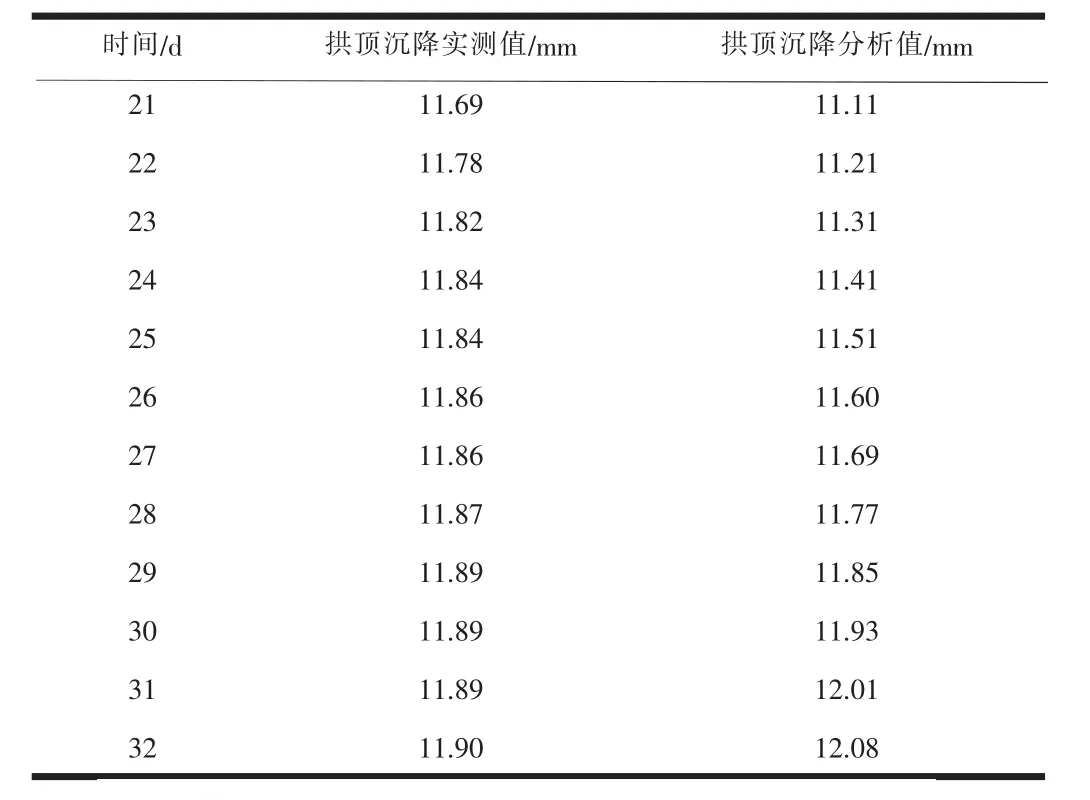
表4 實測數據與分析值對比表

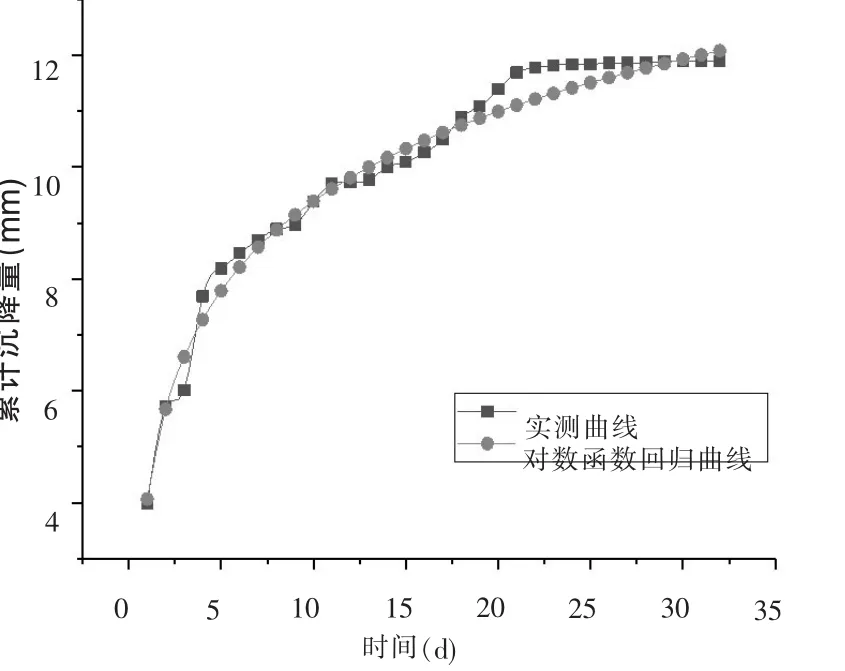
圖6 ZK41+770斷面G3測點拱頂累積沉降量-時間擬合曲線圖

5 結論

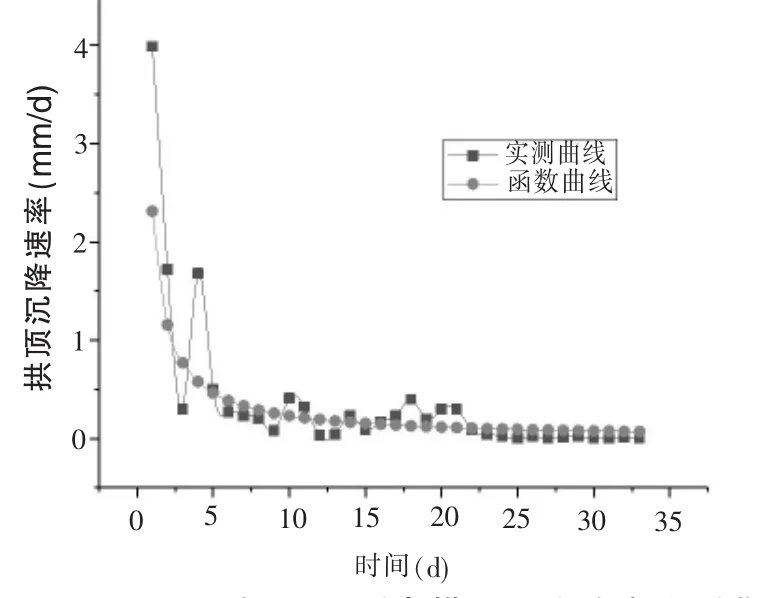
圖7 ZK41+770斷面G3測點拱頂沉降速率實測曲線與函數曲線對比

本文通過某小凈距隧道具體的工程案例，基于斷層破碎帶處隧道拱頂沉降實測值，運用冪函數模型、對數函數模型、雙曲線函數模型和指數函數模型進行回歸分析，建立了關于監測時間與累積沉降量的回歸模型，主要結論如下：

（1）對于該隧道拱頂沉降，對數函數模型回歸效果最好，雙曲線函數模型回歸效果較差；

（2）處于斷層破碎帶上的ZK41+770斷面G3點拱頂沉降共經歷了從急劇變形、緩慢變形到基本穩定三個階段，函數模型預測出拱頂在監測開始的第24天后趨于基本穩定，實測分析結果為第22天以后，實測結果與預測結果相互驗證，使回歸分析的結果具有一定的可靠性，說明回歸分析法可用于不良地質條件下隧道拱頂的穩定性分析以及二襯施作時間的預測；

（3）通過所建立的對數函數模型預測出隧道二次襯砌合理的施作時間為監測開始的第24天左右。