梳理機工作輥結構的優化設計

李志強， 倪 莉， 趙則祥， 張 洪， 梁 穎

(中原工學院 機電學院， 河南 鄭州 450007)

梳理機工作輥結合件是梳理機的關鍵件之一，2個工作輥的工作間隙理想狀況是保持一致性，從而保證梳理通過的纖維層的厚度一致，進而達到高質量的梳理效果，但實際狀況是，工作輥在重力載荷和針布載荷作用下產生撓度，導致工作輥間的隔距不均勻，對梳理機整體性能產生很大影響。目前國外同行業工作輥最大撓度值和間距調整方面做得較好。影響工作輥性能的指標主要有材料和結構2方面，因此，探索工作輥最佳結構成為提高其性能的關鍵之一。作為結構優化概念設計層次的拓撲優化，可從根本上定義結構的形式，是真正意義上的最優設計[1]。1988年，Bendsoe等基于“微結構”思想提出了均勻化方法，由此拓撲優化進入繁榮時期。隨后發展的變密度法，使得拓撲優化的工程應用成為可能[2]。

國內外學者在減少結構撓度和結構優化方面做過很多研究：Yi等[3]提出如何在拓撲優化的結果上建立參數化CAD模型；郭鵬等[4]推導了魚腹型中梁的優化，降低了中梁撓度；王琴等[5]提出基于加載狀態下，動態特性預測的電主軸結構參數優化的思想；陳蘭等[6]對大型船用卷板機上的輥系統進行力學分析和優化，降低了上輥撓度；夏建芳等[7]以主梁幾種主要型鋼結構參數為設計變量，運用ANSYS APDL語言編制了結構優化程序，主梁結構優化結果表明，其應力分布更加合理，最大應力下降4.8%，整體質量下降16%，最大撓度上升50%，仍符合設計標準；李兆凱等[8]分析了二級層級褶皺結構的板模型，在剪切或壓縮載荷下對應的6種失效模式及對應的名義應力。通過比較名義應力值，控制發生的失效模式類型,并結合多目標優化算法，同時進行最小質量和最小撓度的性能優化；Yoshihiro等[9]研究了桁架在自身重力下的全局優化；李志強等[10]研究了以位移約束、應力約束、應變能約束質量最小化為目標的拓撲優化關系。通過對目標函數與約束函數的解析敏度推導,證明了他們之間的等價性。得到的準則方程表明，在最優結構中,單元質量與該單元應變能之比等于結構總質量與結構總應變能之比；Zhu等[11]研究了動力響應下的結構優化，提高了動力性能。

目前，國內在工作輥撓度優化效果上始終沒有達到國外先進水平，為設計出高性能梳理機工作輥，借鑒前人研究優化思路，本文提出采取二步法對工作輥結構進行優化：首先，基于ANSYS APDL平臺應用自編優化程序對工作輥進行拓撲優化，得到工作輥合理拓撲構型；然后，基于該拓撲構型，對拓撲構型建立數學模型，再采用尺寸優化方法對工作輥構型做進一步尺寸優化，最終設計出滿足強度與撓度要求的高性能梳理機工作輥。

1 梳理機工作輥數學模型及優化方法

1.1 工作輥拓撲優化數學模型

工作輥拓撲優化數學模型表達式為

(1)

式中：ρ為設計變量；ρi為連續體第i單元的偽密度；u(ρ)為最大位移；σj(ρ)和[σj]分別為第j個節點的應力及其上限。

由于模型(1)的約束條件隨著有限元模型網格的增多，應力對偽密度的敏度計算會急劇增加，因此，在優化過程中會耗費大量機時，文獻[10]論證了位移、應力、應變能約束的等價性，因此，模型(1)可轉化為應變能最小化問題，更有利于問題的解決，對應的數學模型為

(2)

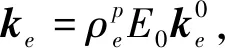
1.2 敏度分析

在優化過程中采用理性數學準則法需要進行敏度分析，針對模型(2)的敏度推導如下

(3)

式中，針布力F2為定值，所以對偽密度的敏度為0。

1.3 工作輥尺寸優化數學模型

在拓撲優化的基礎上，建立結構特征的數字參數化數學優化模型：

(4)

式中：設計變量xi為工作輥各部分結構尺寸；u(X)為最大位移；σj(X)和[σj]分別為第j個節點的應力及其上限。

在尺寸優化過程中，設計變量大大減少，從而敏度分析計算量也相應減少，因此，通過目標函數對設計變量的敏度分析推導出優化準則，然后基于ANSYS仿真平臺進行優化設計，計算耗費時間較少。

梳理機工作輥最大撓度最小化依據上述模型和設計變量對敏度的分析，就可以展開二步優化法的實施：第1步是對工作輥的拓撲優化；第2步是對工作輥的尺寸優化。這2個階段的優化目標函數相同，設計變量不同，因此，優化迭代準則也不同，拓撲優化階段的設計變量為單元的偽密度，尺寸優化有限元模型(FEM)參數化建模中的設計變量為拓撲優化結果中提取的幾何特征，在拓撲優化結果向尺寸優化有限元模型轉變過程中很關鍵，直接影響尺寸優化結果。拓撲優化結果的幾何特征提取應該與優化對象的生產工藝相聯系，避免設計出來而生產不出來的困境，也應該與制造經濟成本聯系起來，盡量做到結構簡單、生產便捷、制造成本低、產品性能優的效果。拓撲優化結果只是提供了材料大體的分布情況，但不能代替第2步的尺寸優化。工作輥優化方案流程圖如圖1所示。

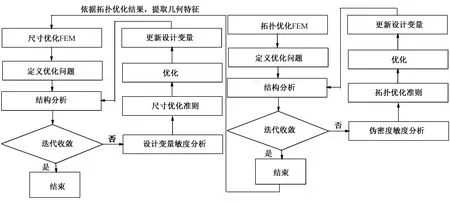
圖1 工作輥優化基本流程Fig.1 Basic procedure of work roll optimization

2 算 例

梳理機工作輥軸承間距為3 891 mm，外徑為 220 mm，滾筒軸長為3 780 mm，軸頭材料為Q235-A圓鋼，滾筒材料為45鋼，彈性模量2.06×1011Pa，泊松比為0.3，密度為7.85 g/cm3，針布質量為 30 kg。工作輥示意圖如圖2所示。

圖2 工作輥示意圖Fig.2 Sketch of work roll

2.1 工作輥構型的拓撲優化

優化前，對國內算例一指定的工作輥進行試驗與仿真，試驗與仿真結果較吻合，工作輥最大撓度為0.3～0.4 mm，國外相同尺寸和材料的工作輥在相同工況下最大撓度稍大于0.1 mm。國內外的區別在于工作輥結構的差異，由此可見合理改變工作輥質量分布可解決最大撓度最小化問題。拓撲優化可打破人們以往根據經驗預判提出最佳結構，然后對提出結構進行尺寸優化的不足，實現真正意義上的結構優化。根據拓撲優化數學模型(2)對工作輥進行拓撲優化，結果如圖3所示。

圖3 工作輥簡化模型剖視圖Fig.3 Section view of work-roll simplified model

工作輥分為2個區域，拓撲優化區域與非拓撲優化區域：非拓撲優化部分是為了保持工作輥功能特性的外形，不參與優化；優化區域是通過拓撲優化對質量進行最佳分布，從而使工作輥最大撓度最小化。按照數學模型(2)，應用ANSYS APDL平臺和自編程序對工作輥進行拓撲優化，找到材料最佳分布，并對拓撲構型結果提取數字特征，為第2步尺寸優化建立參數化數學模型做準備。

圖4示出工作輥的拓撲優化過程中結構材料隨著迭代步數增加，材料分布趨于最優的進化過程。圖中白色區域代表有材料分布，灰色區域代表工作輥沒有材料分布，白色區域外部的黑色區域為優化過程中ANSYS窗口背景。圖4(a)～(f)中工作輥的壁厚從端部向中間逐漸變厚，從而增加了工作輥的剛度，工作輥縱截面類似魚骨型結構，與肋板效果一樣也加強了工作輥剛度，但隨著迭代步數的增加，工作輥內部魚骨狀結構逐漸消失；在圖4(g)～(i)中隨著迭代的收斂，工作輥內部魚骨狀結構已經完全消失，這是因為魚骨狀結構一方面增強了工作輥剛度，有利于減少工作輥最大撓度，但另一方面其存在增加了工作輥質量，這對減少工作輥最大撓度是不利的，這種兩難狀況依賴設計經驗是無法完成的，從拓撲結構的漸變過程來看，利用拓撲優化能清晰穩定地得到材料的最佳分布。在優化結束時，工作輥端部縱截面類似倒放著的M狀結構得到保留，因為工作輥工作時上部承受壓應力，下部承受拉應力，這樣的結構有利于減少縱向應變，從而減少了工作輥的最大撓度。在拓撲優化迭代過程中，材料分布漸變圖反映了迭代過程中材料分布變化的穩定、清晰、快速的收斂過程，收斂的拓撲優化結果圖(見圖4(i))為工作輥第2步尺寸優化提供了結構幾何特征，根據這些幾何特征，建立參數化工作輥幾何模型后就進入了第2步優化階段，即工作輥結構尺寸優化過程。

圖4 迭代過程中工作輥縱剖面結構的演化過程Fig.4 Evolution of work roll rertical section structure in iterative process. (a) Iteration 5; (b) Iteration 6; (c) Iteration 7; (d) Iteration 8; (e) Iteration 9; (f) Iteration 10; (g) Iteration 11; (h) Iteration 12; (i) Iteration 13

2.2 工作輥的尺寸優化

根據拓撲優化結果對工作輥進行參數化建模，如圖5所示。把優化區域中的材料分布用參數化數學模型描述，中間部分可用分段線性函數描述，端部利用曲線擬合，具體選取的擬合函數與零部件生產水平與工藝相關，應與相關企業協商，否則會出現設計出來制造不出來的狀況。算例中的設計變量有工作輥端面厚度、軸頸直徑、空腔兩端用圓臺擬合，中部用階梯錐孔擬合，工作輥壁厚等，從而得到參數化模型。

圖5 工作輥參數化幾何模型Fig.5 Work-roll geometric model with parameters

隨著3D打印的發展，制造業水平得到前所未有的提升，很多復雜結構零件的生產工藝得以解決。在工作輥拓撲優化結果的基礎上，提取數字特征建立參數化數學模型，進入到工作輥尺寸優化階段，按照數學模型(4)，基于ANSYS平臺，應用自編程序對工作輥進行結構優化，也可將模型(4)的問題轉化為應變能約束下的質量最小化問題。優化過程中設計變量的選取很關鍵，直接影響優化效果，這里軸頭直徑也作為設計變量。

圖6示出利用ANSYS軟件創建的工作輥幾何模型的縱剖面。對幾何模型劃分網格、加載、輸入利用敏度推導的優化準則進行尺寸優化，就得到工作輥最優結構。圖7示出工作輥尺寸優化收斂時的一次優化結果。位移云圖顯示，工作輥最大撓度為0.105 mm，約等于0.11 mm，工作輥最大撓度的最小值已經與國外相同材料和工況的同類先進工作輥的性能一致，優化后的工作輥極大改善了工作輥撓度。

圖7 優化后位移云圖Fig.7 Displacement of work-roll after optimization

圖6 工作輥幾何模型縱剖面Fig.6 Vertical section of work-roll geometric model

優化前工作輥最大撓度為0.33 mm，最大應力為7.12 MPa；優化后其最大撓度約為 0.11 mm，最大應力為9.15 MPa。說明優化后的工作輥最大應力有所增大，但遠遠低于許用應力，最大撓度減少了67%。最大撓度發生在工作輥中間，中間壁厚的變化從直觀上看對撓度的影響是一個矛盾，壁厚加厚一方面提高了剛度，但另一方面也加大了自身質量，這個問題無法從直觀經驗上解決，正是某企業工作輥撓度減不下來的問題所在，工作輥端部構形也是遠非經驗和想象可以設計出來的，通過拓撲優化和尺寸優化后工作輥結構異于原結構，材料分布更加合理，工作輥性能得到很大提高。圖8示出未優化時原工作輥結構圖。圖6近似認為優化后的工作輥結構，與優化前的工作輥區別是尺寸參數的變化，結構形式不變。

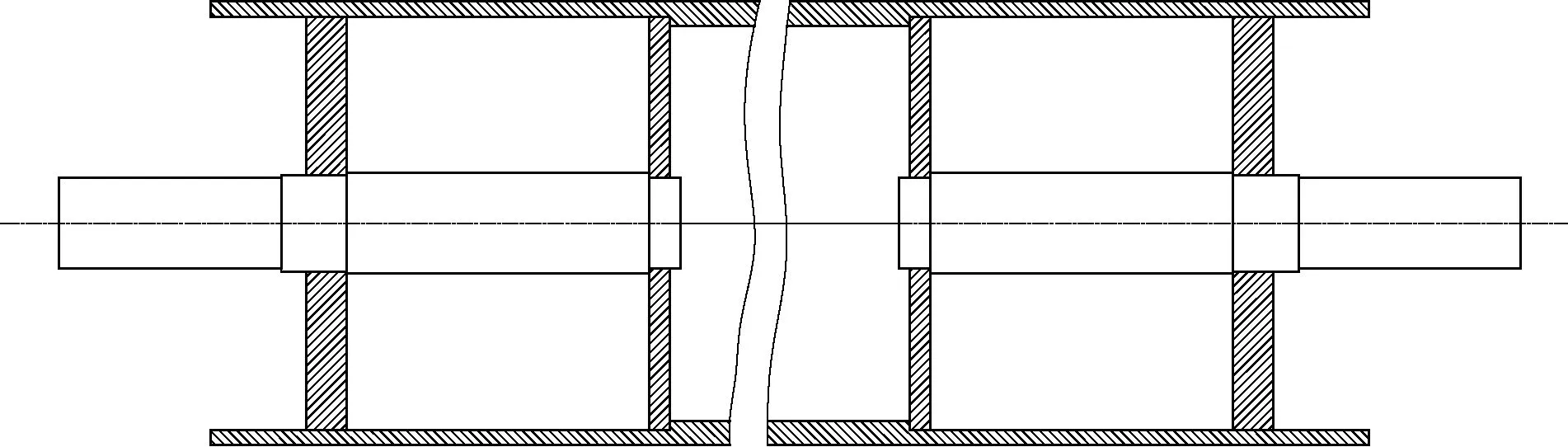
圖8 原工作輥結構圖Fig.8 Structure chart of original work-roll

3 結束語

本文研究了針布載荷和重力載荷下梳理機工作輥結構的拓撲優化和尺寸優化，工作輥結構優化過程分為2個步驟進行：首先對工作輥劃定優化區域與非優化區域，按照給定的數學模型對優化區域進行拓撲優化，找到優化區域最佳材料分布；然后在前一步優化結果的基礎上，抽取材料分布特征，建立參數化數學模型，選定優化方法。基于ANSYS軟件對工作輥進行尺寸優化，獲得工作輥最佳結構，通過算例仿真對比，驗證了優化方法有效性。

優化過程中，采用理性數學準則使拓撲結果更加精確可靠，為工程人員提供了新的設計方法，具有一定的工程應用價值。由于與企業合作過程中未提到工作輥的固有頻率限制，在相應的固有頻率約束下，工作輥撓度最小化需要進一步研究。

FZXB