登月助力航天服下肢關節遲滯模型建立與動力學仿真

李照陽,戴躍洪,唐 鵬,石三川,黃 波

(電子科技大學航空航天學院,成都611731)

1 引言

航天服最主要的功能是為航天員提供空間環境的安全防護并滿足空間操作的活動性能要求[1]。與太空作業不同,月表作業要求航天服上下肢關節系統具備良好的運動性和靈活性,以便完成月面行走、標本采集、設備維修、貨物運輸、科學實驗等艙外作業任務[2]。由于航天服真空防護所造成的余壓(服內外的壓差)作用,當航天員活動時,航天服不可避免地產生相當大的阻力矩[3]。該阻力矩會大大降低航天員肢體運動的靈活度、準確度和平衡性,增加體能消耗,導致航天員月表作業能力和運動能力下降。為適應未來月表低重力環境下的行走需求,航天服下肢關節系統對航天員月表作業任務的影響將作為設計與評價其助力性能的依據。

近些年,為提高航天員著服后的活動性能,常在對應的人體關節如肩、肘、髖、膝處加入軟式關節結構,如平褶式[4]、波紋式[5]、橘瓣式[6]和等張立體式[7]等,但這些關節結構復雜,容易受設計和加工工藝水平影響。Sim[8]和Judnick等[9]先后提出了機械反壓(Mechanical Counter Pressure)方案,但機械反壓航天服對材料選取與加工工藝要求較高,且僅對人體局部起到壓力防護作用。NASA和佛羅里達州人與機器認知研究機構(IHMC)共同研發X1航天員專用外骨骼服,采用聯合設計模式將外骨骼與航天服材料結合,增加航天服機動與負重能力[10]。郭慶等[11]提出一種主動航天服方案,在現有航天服的基礎上運用外骨骼機器人技術,并融入傳感、控制、信息等技術,使其成為高度人機耦合的復雜力量隨動系統。以上2種方案都未考慮航天服關節遲滯特性對控制系統的影響。

本文參考美國艙外活動單元(Extravehicular Mobile Unit,EMU)公開數據,提出一種登月助力航天服結構方案,分析航天員月表行走時下肢關節的遲滯模型和運動范圍,建立航天服下肢關節阻力矩-角度映射關系,并完成二連桿動力學仿真分析,為后續隨動控制提供理論基礎。

2 助力航天服外骨骼結構

登月助力航天服是將力量增強型外骨骼助力技術運用到現有航天服,提高航天員的承載能力、抓舉能力和運動能力,幫助航天員安全、快捷、高效、省力地實現月面行走、樣本采集、裝備維修等月表作業任務。其結構主要包括：①機械結構。采用仿生技術和機器學習技術,滿足航天員個性化的運動要求以及艙外航天服結構尺寸,實現機械承載和助力；②感知系統。通過多傳感器和數據融合技術等感知航天員的運動姿態和生理狀態等,同時較為準確地預測航天員的運動意圖；③控制系統。針對航天員的動作需求,通過多功能傳感與柔順耦合控制技術實現外骨骼的多自由度、助力隨動的控制目標；④驅動機構。根據控制系統指令,綜合應用電機、液壓等驅動方式,實現輕質、大功率、小型化的驅動助力；⑤能源系統。提供各系統所需的能源。

圖1為設計的登月助力航天服的下肢關節外骨骼結構圖。登月助力航天服下肢關節外骨骼具體尺寸參考美國EMU艙外航天服的公開數據,仿人設計實現結構的助力和穿戴舒適,碳纖維材料的設計加工實現輕質、高強度的外骨骼；采用肌電、慣性、壓力傳感器等多傳感器感知和數據融合技術實現步態識別在線辨識和運動意圖準確預測；安裝4個Maxon電機于髖、膝關節處,通過控制電機驅動實現助力。

圖1 登月助力航天服下肢關節外骨骼結構Fig.1 Exoskeleton structure of lower limb joints in lunar assist space suit

3 航天服下肢關節遲滯模型

航天員在執行月表作業任務時,行走、彎腰拾物、起蹲等動作的實現都需要人體下肢各關節的參與配合。本文主要研究航天員在矢狀面內的行走,其運動姿態可劃分為支撐相和擺動相,主要表現為下肢關節角度的規律變化。而航天服因為充壓設計(EMU,29.67 kPa)導致關節阻力矩具有極強的遲滯效應,具體表現為關節阻力矩不僅與當前關節角度有關,而且與關節歷史運動角度有關,具有高度的非線性和遲滯性,使得普通函數無法實現對阻力矩的準確描述[12]。同時,登月助力航天服要實現關節助力效果,需要分析航天服下肢關節的遲滯特性,建立下肢關節阻力矩-角度映射關系,為后續的動力學方程建立提供關節阻力矩函數。

國內外對艙外航天服阻力矩的測量裝置主要有NASA基于fish-scale方法的結構[13]、MIT的內置式機器人RSST(Robotic Space Suit Tester)[14]以及國內的外置式機器人[3]。本文根據fish-scale方法搭建下肢關節阻力矩測試裝置,系統包括內壓為29.67 kPa的充氣下肢、0～50 Nm扭矩傳感器、-180°～180°角度傳感器、0～30 kg拉壓力傳感器和相應固定機械機構,其結構示意圖如圖2所示。

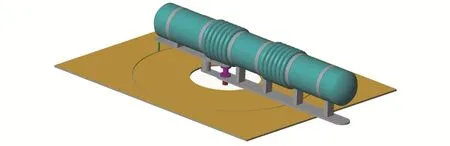
圖2 下肢關節阻力矩測試裝置Fig.2 Measuring device of joint resistance torque in lower limbs

選擇應用最為廣泛的Preisach遲滯模型[15]描述已得到的下肢關節阻力矩-角度映射關系。該模型是一種完全數學模型,利用數學公式來模擬遲滯曲線,能較精確地描述遲滯特性,其模型的數學表達式為式(1)：

式中,u(t)表示當前時刻t的輸入,f(t)表示當前時刻t的輸出,γα,β[u(t)]為基本遲滯變換函數,如圖3所示。α和β(α≥β)分別表示向上和向下變換的變換點,μ(α,β) 是γα,β權重函數。

基本遲滯變換函數γα,β只有兩個輸出值+1和-1。確定方法為：當輸入u(t)＞α時,γα,β[u(t)]=+1；當輸入u(t)＜β時,γα,β[u(t)]=-1。 當輸入介于α和β之間時,若輸入u(t)沿著 ABCDE的方向逐漸上升,γα,β[u(t)]=-1；若輸入沿著 EDFBA 的方向逐漸下降,γα,β[u(t)]=+1[16]。 通過γα,β的加權組合引入方向性和記憶性,從而描述遲滯現象。

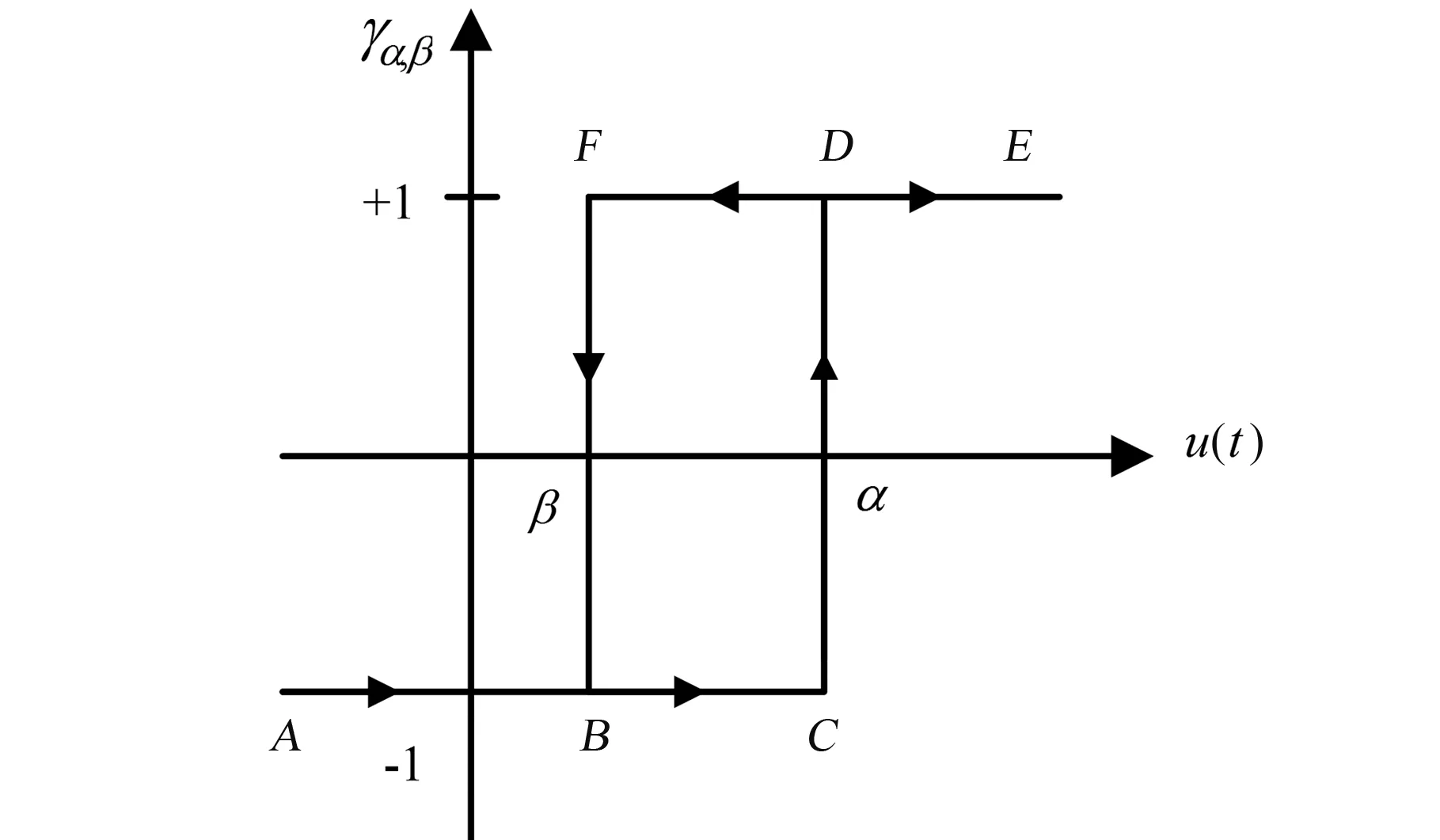
圖3 基本遲滯變換函數Fig.3 Elementary hysteresis transform function

其中,輸出f(t)的積分區域為S,其大小為S={(α,β)α＞β,α＜αmax,β＞α0},其中α0＜αmax為積分區域α軸上的某一特定值,如圖4所示。

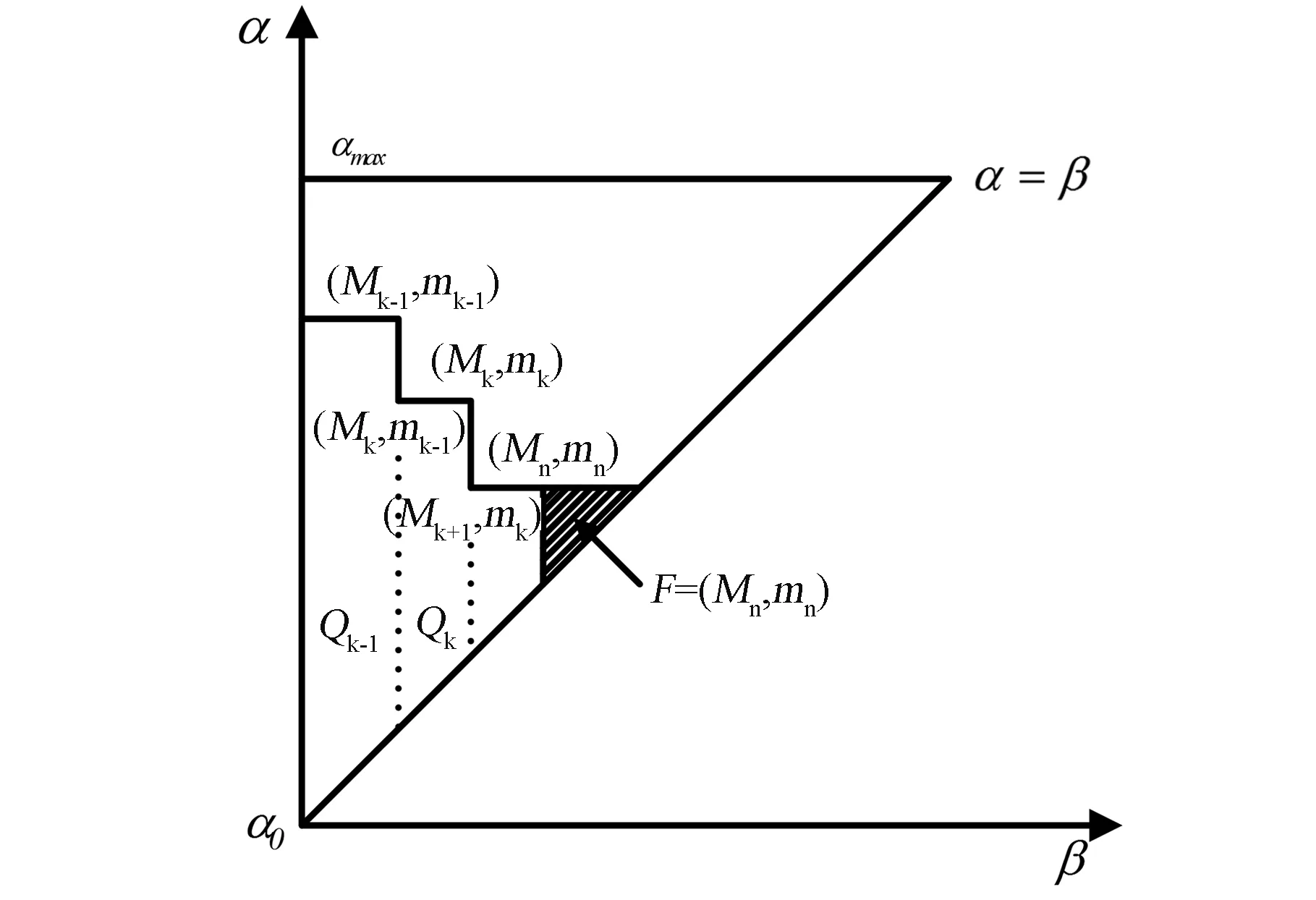
圖4 Preisach(α-β)積分區域的幾何表示Fig.4 Geometrical representation of Preisach(α-β)integral area

積分區域S根據關節運動軌跡劃分為S+區域(基本遲滯變換函數γα,β輸出為+1)、S-區域(基本遲滯變換函數γα,β輸出為-1)和邊界L(t)(由坐標點(Mn,mn)構建的階梯形),這樣輸出f(t)可以表示為式(2)：

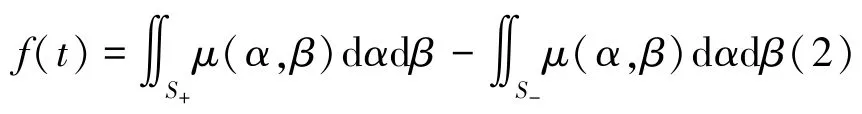
定義灰色三角形區域的積分值為F(Mn,mn),那么矩形區域Qk的積分值可以表示為式(3)：

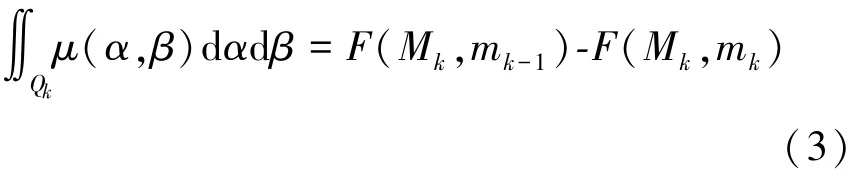
將輸出f(t)的積分式(2)離散化,可得式(4)：

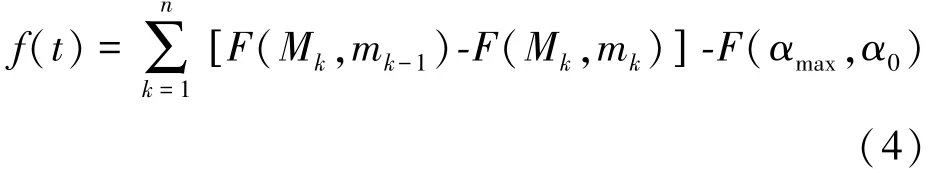
通過式(4),僅需要得到邊界L(t)的坐標點(Mn,mn)對應的F(Mn,mn)就可以得到關節阻力矩輸出值f(t)。

4 助力航天服下肢外骨骼動力學分析

4.1 登月助力航天服下肢外骨骼模型

航天員的行走平面可以分為額狀面、水平面、和矢狀面。在行走時,額狀面和水平面的相對運動較少,為簡化計算,在進行人體下肢建模時僅關注航天員行走時矢狀面內髖關節、膝關節和踝關節的角度變化[17]。而人體下肢的運動是人體肌肉及韌帶帶動骨架繞關節的旋轉運動,因此人體左右大腿、左右小腿、左右足分別可以簡化為單連桿結構,各桿之間通過關節連接。但由于踝關節運動范圍較小且結構復雜,故將左右足和左右小腿構成一個整體,而左右兩肢受力一樣,因此將下肢簡化成二連桿機構,具體如圖5所示。

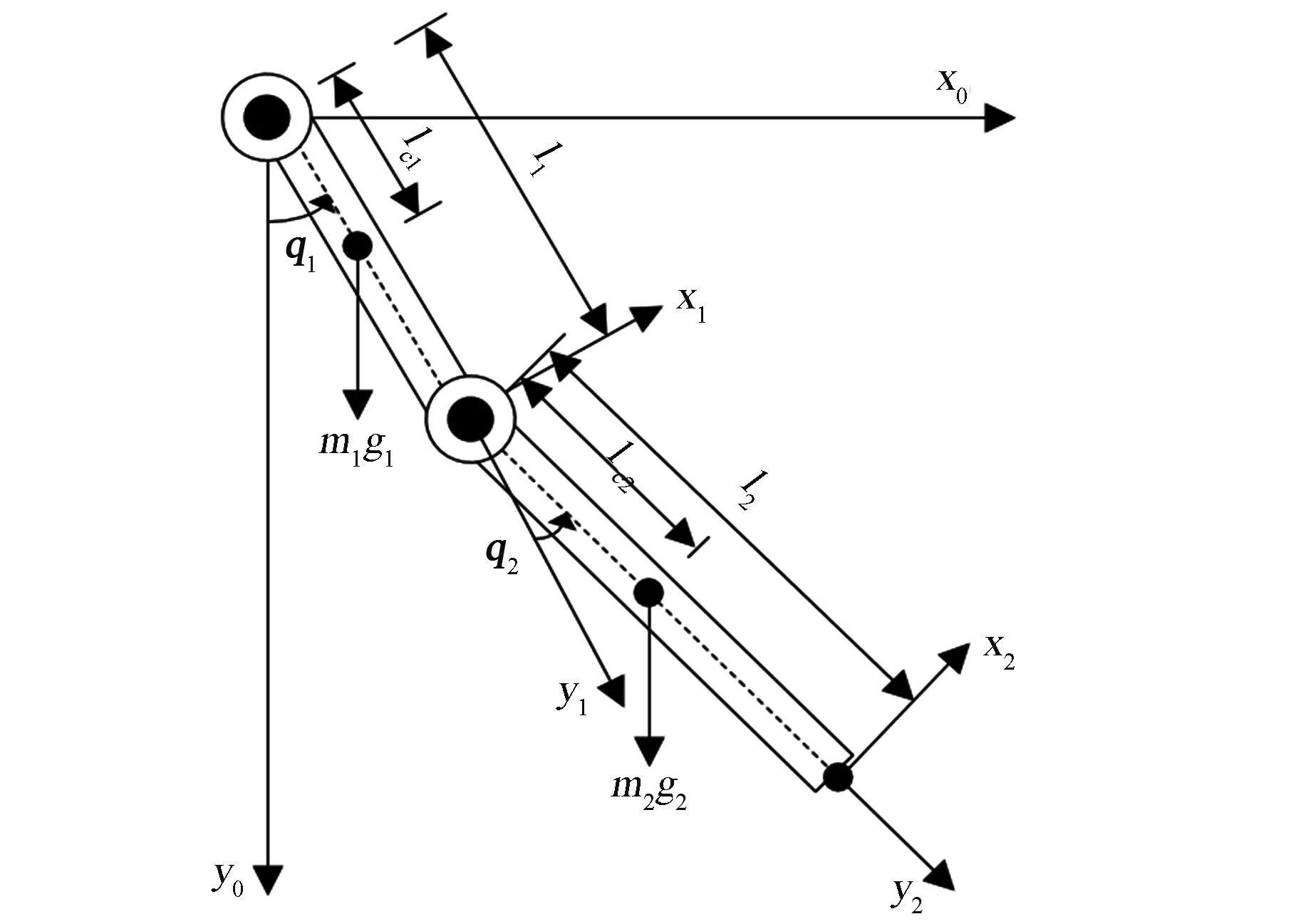
圖5 下肢二連桿簡化模型Fig.5 Two-link simplified model of lower limbs

圖中,i=1,2,其中qi表示關節轉角,li表示連桿i的長度,lci表示上一個關節與連桿i質心的長度。

4.2 牛頓-歐拉動力學方程

相對于拉格朗日動力學建模方法,牛頓-歐拉法適用于多桿機構的動力學分析與計算機編程計算。由于登月航天服下肢模型較為簡單,容易得到二連桿之間的耦合關系以及單個連桿的受力情況,可以通過使用廣義坐標下qi及其導數求解連桿i的速度q·i與加速度q¨i,然后反向迭代計算連桿i的作用力fi和作用力矩τi[18]。連桿i質心加速度ac,i可以表示為式(5)：

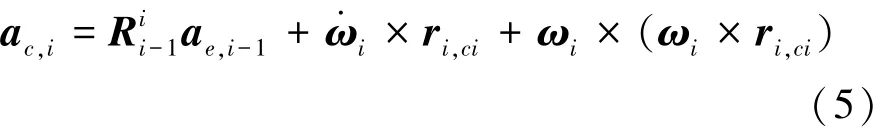
式中,Rii-1為坐標系Oi-1到坐標系Oi的旋轉矩陣,ωi為連桿i角速度,ω·i為連桿i角加速度,ri,ci為從點oi到連桿i質心oci的向量,ae,i-1為連桿i-1的末端加速度,則連桿i的末端加速度ae,i可以表示為式(6)：

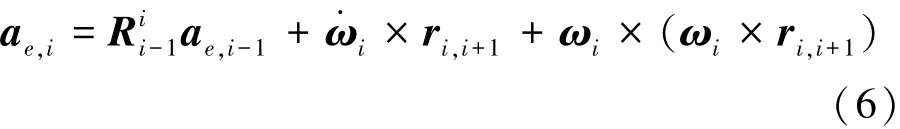
式中,ri,i+1為從點oi到oi+1的向量,其代替式(5)的ri,ci。連桿i力平衡方程可以表示為式(7)：

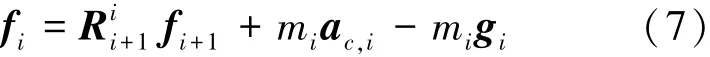
式中,fi+1為連桿i+1施加到連桿i上的力,mi為連桿i的質量,gi為連桿i的重力加速度,可以表示為式(8)：

式中,g為地球重力加速度。連桿i力矩平衡方程可以表示為式(9)：

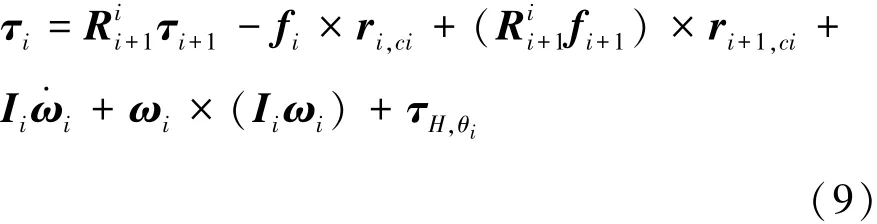
式中,τi為連桿i-1施加到連桿i上的力矩,Ii為連桿i的轉動慣量,τH,θi為航天服 Preisach模型得到的關節阻力矩。

對于登月航天服下肢模型,已知以下向量,見式(10)、(11)：

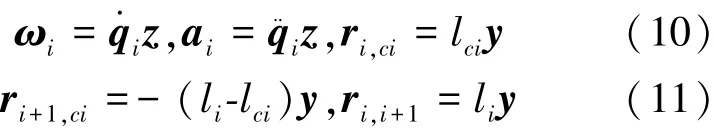
其中,x、y、z分別表示基座坐標系的3個單位坐標向量。

通過公式(5)可得到連桿1質心加速度ac,1和連桿 2 質心加速度ac,2,見式(12),(13)：

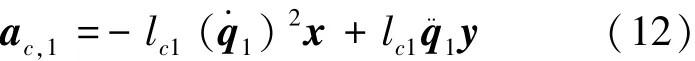
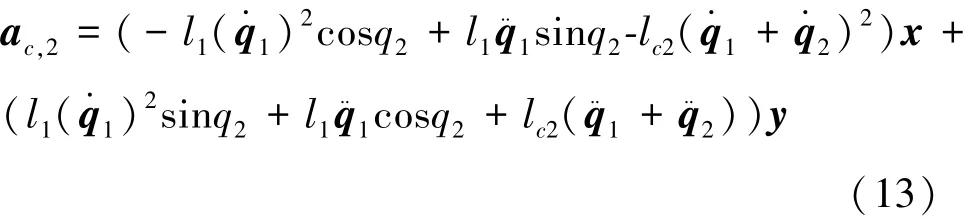
通過公式(6)可得到連桿1末端加速度ae,1,見式(14)：

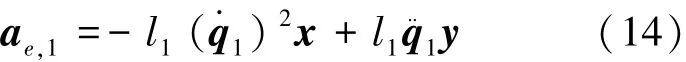
通過公式(8)可得到連桿1質心加速度g1和連桿2質心加速度g2,見式(15),(16)：

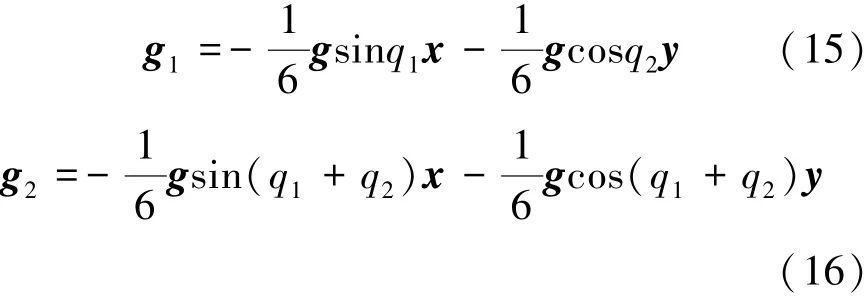
由于登月航天服下肢關節處加驅動機構,協助航天員完成月面行走任務,其驅動力大小可以通過公式(9)得到式(17)、(18)：

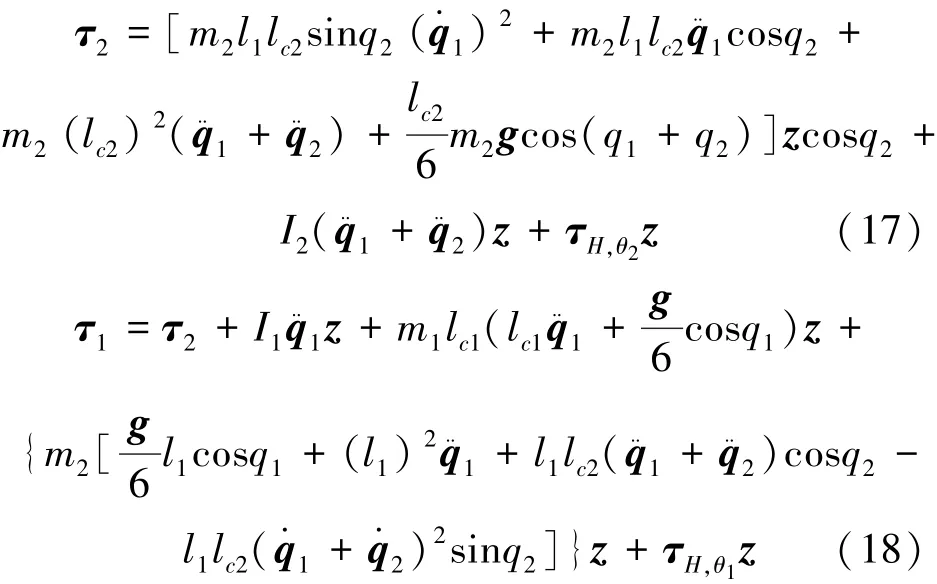
5 仿真分析

5.1 下肢運動參數

根據中國航天員的選拔條件,即年齡23到35歲,身高 1.6～1.72 m,體重 55～70 kg,對比國內4名男性航天員的身和體重參數[19],結合《GB/T10000-1988中國成年人人體尺寸》[20]擬定男性航天員身高為1683 mm,體重為59 kg,大腿長l1為466 mm,小腿長l2為370 mm。再參考《GB/T17245-2004成年人人體慣性參數》[21]作為人體相對質量分布、質心相對位置以及人體體段轉動慣量數據來源。其中,m1表示為人體大腿質量(kg),m2表示為人體小腿質量(kg),lc1表示為人體大腿質心距離(mm),lc2表示為人體小腿質心距離(mm),Iz1表示為人體小腿長度(mm),Iz1表示為人體大腿轉動慣量(kg·mm2),Iz2表示為人體小腿轉動慣量(kg·mm2),具體數值如表1所示。

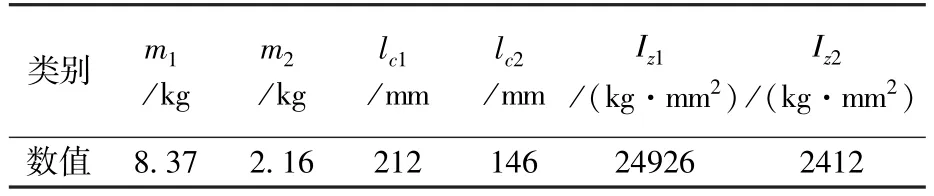
表1 下肢關節主要設計參數Table 1 Design parameters of the lower limb joints

利用Opensim肌肉骨骼系統軟件模擬人體正常行走運動,使用系統自帶的Leg6Dof9Musc模型,修改其中參數,得到航天員著服后下肢關節角度變化。 其中,髖關節為-29.75°～16.92°,膝關節為-68.69°～3.07°。根據美國EMU航天服在29.67 kPa內壓情況下,關節運動范圍平均減少約15%[22]。因此,擬定在1個步態周期內,髖關節運動范圍為-25°～15°,膝關節運動范圍為-60°～0°,如圖 6 所示。

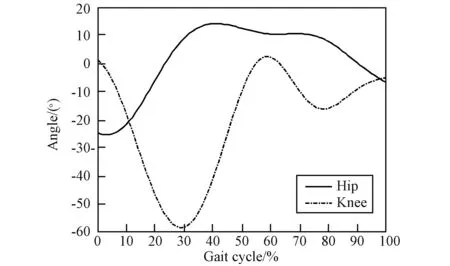
圖6 下肢關節角度變化曲線Fig.6 Changes of joint angle in lower limbs

5.2 動力學仿真

根據5.1節下肢運動參數,在Creo軟件中設計并裝配出航天員下肢模型。由于人體骨骼十分堅硬,因此在不考慮變形的情況下,可以視人體的各部分為剛體,視關節為鉸鏈。在自由度配置方面,設計髖關節、膝關節和踝關節各只需1個自由度,下肢模型通過保存為Parasolid格式文件導入到ADAMS中,賦予各構件的材料屬性,修改質量信息,根據下肢運動參數設置模型構件的質量和轉動慣性數值,在髖關節和膝關節處定義轉動副,而在踝關節處定義固定副,將足部固定在小腿處。仿真模型如圖7所示。

考慮到登月助力航天服中外骨骼的作用之一是幫助航天員克服航天服內余壓的阻力,為了模擬出航天服對航天員運動的阻礙作用,在髖關節和膝關節處設置了2個單向力矩函數來模擬航天服的關節阻力,其中模型中的權重函數μ(α,β)需要通過試驗測得,為避免構件重力的影響,在ADAMS中設置3個方向的重力加速度為0。

圖7 下肢二連桿結構仿真模型Fig.7 Two-link structure simulation model of lowerlimbs

通過仿真可以得到髖關節的阻力矩隨關節角度變化曲線,如圖8所示,其中Flexion表示航天員髖關節從15°彎曲至-25°,Extension表示航天員髖關節從-25°伸展至15°。可以看出,髖關節前伸時阻力矩要小于后曲時的阻力矩,主要原因是因為仿真時髖關節正處于向后彎曲的動作。其中,登月助力航天服充壓狀態下髖關節Flexion方向力矩范圍為-84.68～52.51 Nm,Extension方向力矩范圍為-86.95～45.89 Nm。

膝關節的阻力矩隨關節角度變化曲線如圖9所示,其中Flexion表示航天員髖關節從0°彎曲至-60°,Extension表示航天員髖關節從-60°伸展至0°。可以看出,膝關節伸展時阻力矩要小于彎曲時的阻力矩,因為仿真時膝關節正處于向后彎曲的動作。其中,登月助力航天服充壓狀態下膝關節Flexion方向力矩范圍為-14.55～13.58 Nm,Extension方向力矩范圍為-13.52～13.52 Nm。由圖8、9可以看出登月助力航天服下肢柔性關節在前屈/后伸時關節阻力矩相對于關節角度的變化關系呈明顯的遲滯特性。同時也證明航天服柔性關節阻力矩不僅與當前關節角度有關,而且與關節運動方向有關,與文獻[23]、[12]一致。

已知航天員在1個步態周期內下肢關節角度變化曲線和充壓(EMU,29.67 kPa)后登月航天服關節阻力矩-角度映射關系曲線,為了實現對1個步態周期內的電機控制,需要結合上述曲線得到關節阻力矩隨步態周期變化曲線,如圖10所示。由于在1個步態周期內,下肢關節運動角度和運動方向實時發生變化,特別是在髖關節,運動方向變化頻繁,容易導致阻力矩突變。為了實現電機的柔順控制,對關節阻力矩-步態周期映射關系進行數據擬合處理,采用MATLAB的高階正弦函數逼近(Sum of Sin Functions)關節阻力矩隨步態周期變化曲線。其中,髖關節在1個步態周期內力矩范圍為-85.54～54.15 Nm,膝關節在1個步態周期內力矩范圍為-13.58～18.19 Nm。

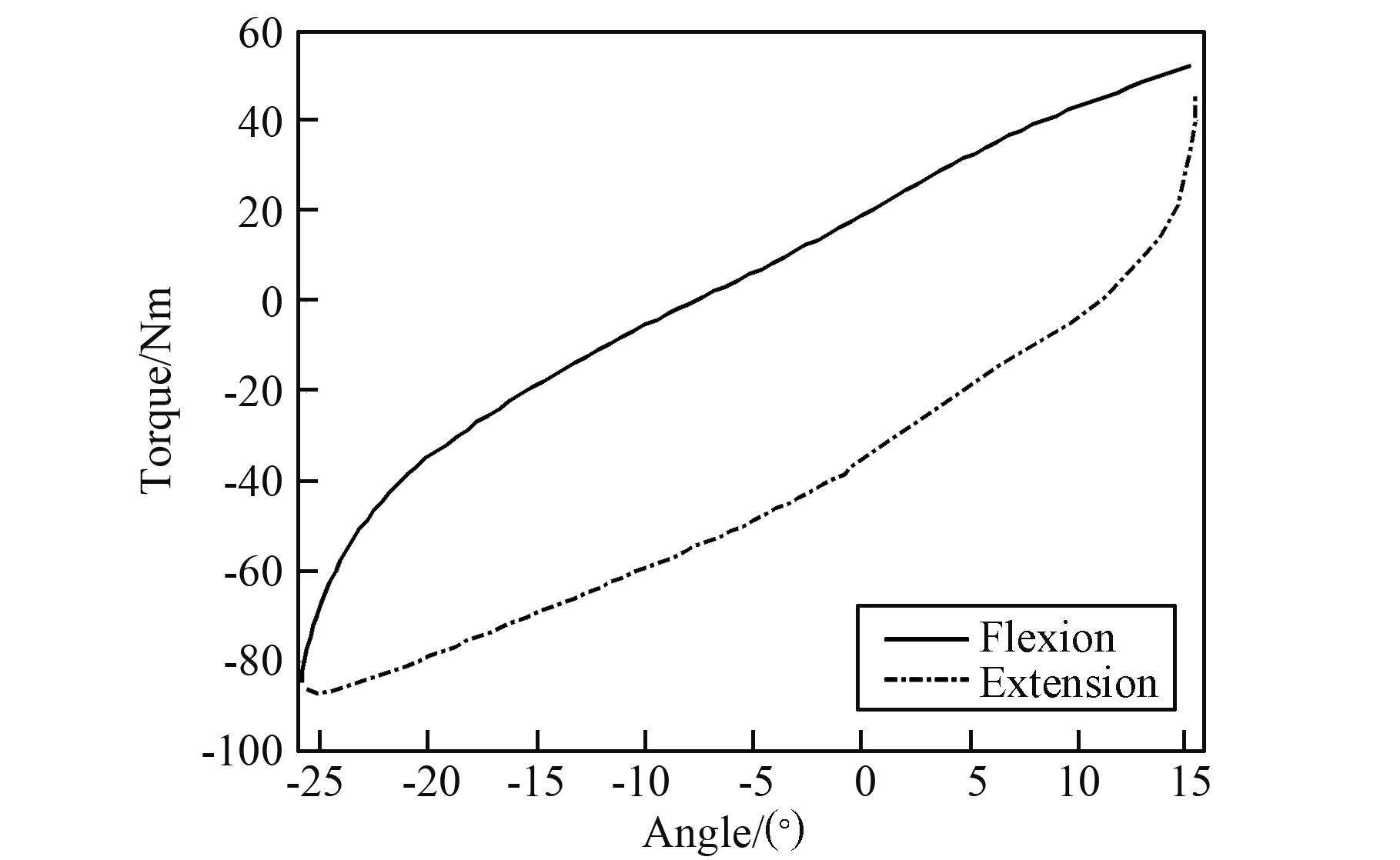
圖8 登月航天服髖關節阻力矩-角度曲線Fig.8 Damping torque-angle curves of hip joint inlunar spacesuit

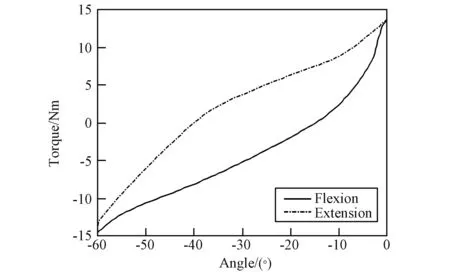
圖9 登月航天服膝關節阻力矩-角度曲線Fig.9 Damping torque-angle curves of knee joint in lunar spacesuit

得到登月助力航天服關節阻力矩-步態周期的擬合函數,可以在下肢髖關節、膝關節處添加2個阻力矩函數,根據登月助力航天服下肢外骨骼動力學方程求解下肢關節的驅動力矩。同時為了模擬月面低重力環境,需要修改ADAMS系統的重力加速度,其值為1/6 g。登月助力航天服下肢關節驅動力矩隨步態周期變化曲線如圖11所示。其中,下肢關節驅動力矩在步態周期50%左右變化較大,說明當支撐腿在將要離開地面時會造成關節驅動力矩的突變。同時髖關節在1個步態周期內驅動力矩范圍為-99.65～124.43 Nm,膝關節在1個步態周期內驅動力矩范圍為-27.78～32.78 Nm,對比圖10,說明一個步態周期內航天服關節阻力矩在驅動力矩所占比例可達50%左右,使得航天員需要消耗更多的能量來完成相應的動作。

圖10 登月航天服關節阻力矩-步態周期曲線Fig.10 Damping torque-gait cycle curves of joint in lunar spacesuit

6 結論

在未來月面正常行走過程中,航天員下肢關節的運動角度和運動方向呈現周期性變化,導致航天服關節阻力矩突變。通過遲滯模型建立與分析,髖關節在0°時,不同的運動方向導致阻力矩相差54.34 Nm,而膝關節在-30°時,不同的運動方向導致阻力矩相差8.87 Nm。通過對登月助力航天服下肢關節動力學仿真,模擬月面低重力環境,得到1個步態周期內下肢關節阻力矩和驅動力矩變化曲線,且關節阻力矩在驅動力矩所占比例可達50%左右。仿真結果為后續驅動機構的力矩控制提供理論參考。未來工作主要集中在低重力環境對航天員步態的影響以及驅動機構運動控制系統研究。

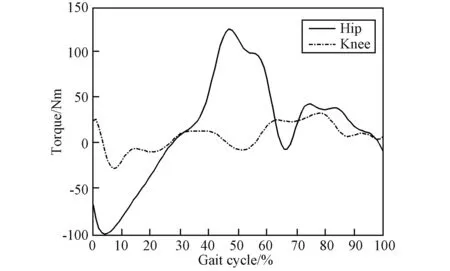
圖11 下肢關節驅動力矩-步態周期曲線Fig.11 Driving torque-gait cycle curves of lower limb joint