基于UG/NX Nastran的發動機連桿三維設計及優化

劉秀清,楊彬彬,王雪強

(山東理工大學 交通與車輛工程學院, 山東 淄博 255049)

連桿作為發動機中的重要零件之一，是重要的動力傳遞部件。連桿的工作環境惡劣，受力狀況復雜，工作的同時承受著活塞傳來的氣體壓力、往復慣性力及其本身擺動時所產生的慣性力的作用，經受拉伸、壓縮和彎曲等交變載荷的共同作用[1-2]。隨著發動機產業的發展，各企業對減小連桿質量、減小連桿工作應力等要求也越來越高[3]。因此對連桿進行有效的優化設計和受力分析非常重要[4]。

本文采用UG軟件對發動機連桿進行三維設計，以體積最小、質量最輕為目標，采用NX Nastran進行分析與優化，以期得到最優化方案。

1 有限元模型的建立

1.1 NX Nastran介紹

NX Nastran是由西門子公司研發的高級計算機輔助工具，全球大多數機械廠商都采用該工具進行優化與分析。NX Nastran分析設計包含應力、位移、振動、波動、溫度、磁場、聲學與噪聲、電流電壓等方面[5]。該工具能夠進行網格化、添加載荷、定義材料、定義約束和邊界條件等，能夠制定特殊有限元分析模型，支持通用工程仿真，最常見的是線性受力分析和非線性受力分析[6]。

1.2 連桿幾何模型的建立

幾何模型是分析問題的基礎，使用UG/NX復合建模時，主要采用特征添加的方式創建連桿的各個零件模型并裝配三維模型。以165F型發動機連桿建立的完整裝配模型如圖1所示，以大頭指向小頭的方向為Z軸的正方向。

圖1 連桿的完整模型Fig.1 The complete model of connecting rod

在將UG/NX中建好的連桿模型導入到有限元軟件之前，一定要注意參數特征，尤其是作為優化目標設計變量的參數。進入NX Nastran有限元解算器之后，要定義好設計變量和目標變量，這樣的參數化建模體現在參數的傳遞以及目標優化的具體過程中[7]。

1.3 連桿有限元模型的建立

對連桿的主體部分幾何模型采用精度較高的六面體單元劃分網格，其余部分采用四面體單元劃分網格，同時設置單元的大小為1mm進行網格劃分，連桿有限元模型的單元數目為29 808個，節點數目為90 831個，連桿有限元模型如圖2所示。

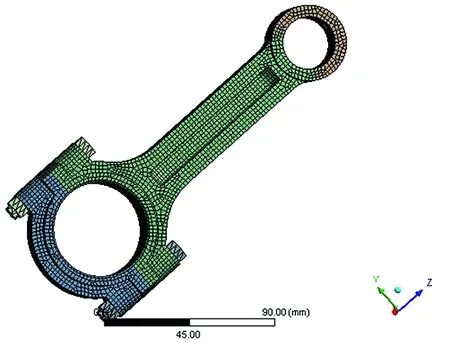
圖 2 連桿的有限元模型Fig.2 The finite element model of the connecting rod

2 連桿的靜力分析

2.1 連桿的結構特點

研究的連桿采用平切口55號鋼模鍛件，經機械加工和熱處理完成。連桿大頭、連桿蓋通過螺栓及其預緊力與連桿緊緊結合在一起。桿身的橫截面呈“工”字形，且與連桿大、小頭圓滑過渡。連桿小頭設有活塞銷潤滑油孔，但是尺寸比較小，在分析時可以忽略潤滑的影響。忽略連桿大頭的軸瓦定位槽，以Z軸為豎直方向，連桿可視為左右對稱及前后對稱結構。為便于分析，建模時忽略了較小的圓角，桿身與大頭和小頭的圓滑過渡也給以忽略，這樣可以節省出大量的空間以便于有限元分析計算[8]。

2.2 連桿材料的力學特性

連桿材料的主要力學特性見表1。

表 1 連桿材料的特性
Tab.1 Material properties of the connecting rod

密度/kg·m-3抗拉強度/MPa屈服強度/MPa伸長率/%收縮率/%7 8506453801335

2.3 連桿優化邊界條件

2.3.1 約束邊界條件

建立連桿模型時，以大頭的連接螺栓及螺母為例，這樣便于施加邊界約束條件及載荷。

(1)連桿蓋的約束

最大壓縮情況下，連桿蓋和桿身通過螺栓連接在一起，對桿身的約束就可以限制連桿蓋；最大拉伸情況下，連桿蓋會有應力和應變產生，在Z方向被拉伸，Y方向變窄，所以要限制X向位移。

(2)桿身的約束

因為連桿上下面有沿Z方向拉伸和X方向變薄的趨勢，而Y方向變化小，所以要限制Y向位移。

(3)大頭的約束

模擬中，對連桿大頭內表面的X、Y和Z方向的位移進行約束。

(4)小頭的約束

連桿在拉伸和壓縮時，最大應力應變均出現在連桿小頭或小頭與桿身的過渡處，因此可以對大頭約束，只在小頭內表面施加載荷。

2.3.2 載荷邊界條件

根據《柴油機連桿設計手冊》可知，與該連桿匹配的活塞尺寸D*S=65*70(mm*mm)。最大壓縮情況下燃氣最大壓力為6.5 MPa，作用在連桿上的的最大燃氣壓力為

式中：D為活塞的直徑；Pmax為燃氣最大爆發壓力；f為動載系數。根據進氣沖程燃燒室初始低壓2.5 MPa，同理可計算作用在連桿上的最大拉力為12 444 N。

軟件中直接添加標準重力加速度，可實現慣性力的模擬。離心力也無需計算，只要給連桿添加相應的轉速就可以實現。連桿的轉速為2 600 r/min，轉化成角速度為263 rad/s，可以直接加到連桿的邊界條件中[9]。

2.4 連桿的靜力分析

本文對連桿的兩種極限工況，即最大壓縮和最大拉伸工況進行靜力分析，分析連桿的應力狀態。

由圖3可知，壓縮狀態最大應力出現在連桿小頭與桿身的過渡凹槽處，最大值為161.41 MPa，此處就是連桿的危險部位，但其最大應力遠遠小于材料的屈服極限。最小值出現在連桿蓋外側，連桿小頭上端和大頭下端的應力相對較小。隨著桿身向大頭孔的靠近應力逐漸減小，但變化幅度不大。

圖3 連桿壓縮狀態應力云圖Fig.3 The stress cloud map of the connecting rod at compression state

圖4給出了連桿在拉伸工況下的應力分布，最大應力值仍然出現在連桿小頭與桿身的連接處，最大應力值為88.457 MPa；最小值出現在連桿大頭端蓋，桿身的應力變化趨勢與壓縮工況大體相同，并且小頭與大頭的應力值都比較小，同樣符合實際情況。

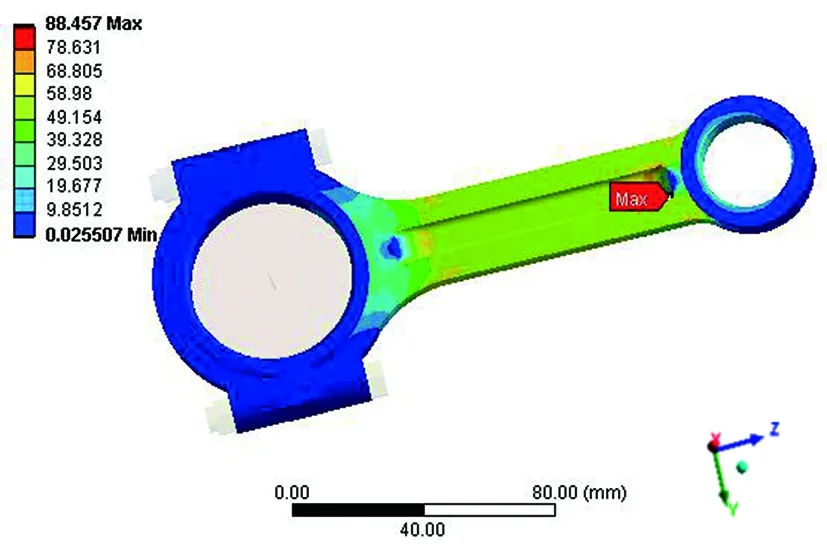
圖4 連桿拉伸狀態應力云圖Fig.4 The stress cloud map of the connecting rod at tensile state

由連桿在壓縮和拉伸兩種工況下的應力分布圖可知，連桿的最大應力出現在小頭與桿身的過渡處，應力的最大值都在極限范圍內，其中壓縮時的安全系數為

(1)

拉伸時的安全系數為

(2)

式中σs為屈服應力。可見兩種工況下連桿都符合強度要求。

由上述分析可知，為了增強連桿的強度，減小變形，在連桿的設計制造時，合理范圍內要保證桿身與大、小頭的過渡處有足夠大的圓弧過渡，還應在連桿大頭和連桿蓋上布置加強筋和凸臺。

3 連桿的優化設計

3.1 連桿的優化設計分析

以最大壓縮狀態的連桿受力為基礎進行連桿的優化設計。優化目標：連桿質量最小；優化約束：應力不超過屈服極限；優化參數：桿身厚度、槽寬、小頭厚度。

3.2 優化前后的參數比較

優化前后的模型參數見表2， 為便于實際加工制造，將參數圓整修正成為便于加工的數據，再次校核其強度。修正后的參數見表 2，連桿質量減小了6.27%，以其為最終的優化方案[10]。

表2 連桿優化前后的參數
Tab.2 Parameters of the connecting rod before and after optimization

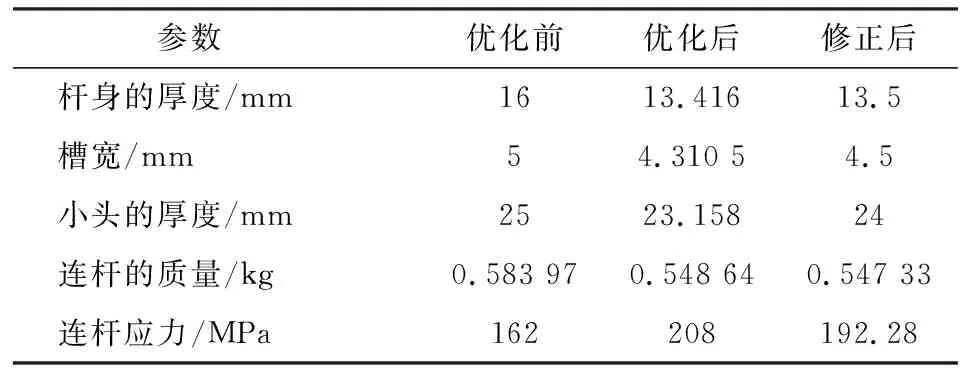
參數優化前優化后修正后桿身的厚度/mm1613.41613.5槽寬/mm54.310 54.5小頭的厚度/mm2523.15824連桿的質量/kg0.583 970.548 640.547 33連桿應力/MPa162208192.28

3.3 優化后連桿的靜力分析結果

由圖5可見，優化后的連桿，應力增大了46 MPa，但質量減輕了6.05%。由于桿身變薄，其應力有所增加，但仍在屈服極限范圍內，符合強度要求。

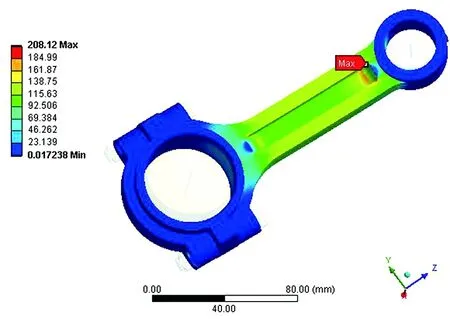
圖 5 優化后連桿的應力圖Fig.5 The stress diagram of the optimized connecting rod

圖6給出優化后連桿的變形圖。由圖6可以看出，優化后的連桿變形有所增大，變形的變化趨勢與優化前一致。

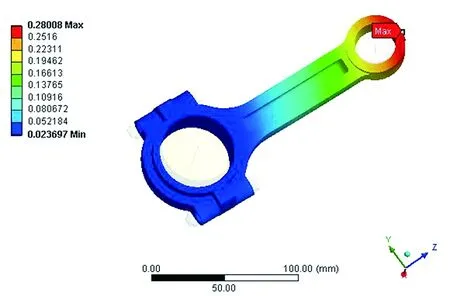
圖6 優化后連桿的變形圖Fig.6 The deformation pattern of the optimized connecting rod

3.4 優化后模型的穩定性分析

優化后的連桿模型質量減輕、長度不變、桿身變薄，可能會影響到連桿的穩定性，所以需對其穩定性進行驗證。

對優化后的模型定義新的分析類型,進行線性屈曲分析，得到屈曲載荷因子(見表3)。由于各階載荷乘子都大于1，因此不會出現失穩的情況，穩定性不會因為優化結果而受到影響。

表3 線性屈曲分析的模態
Tab.3 The mode of linear buckling analysis

名稱階次屈曲載荷因子一階屈曲模態12.263 1二階屈曲模態26.385 1三階屈曲模態354.396

4 結束語

利用UG/NX軟件建立了連桿三維模型，通過NX Nastran有限元解算器進一步完善了模型，并進行了靜力強度分析。以連桿質量最小為優化目標，以應力不超過屈服極限為約束條件，對連桿的桿身厚度、槽寬、小頭厚度等參數進行了優化并選出了最優設計方案。同時根據實際加工的要求，對參數進行了圓整優化。為保證質量減輕后連桿穩定性仍滿足要求，對新模型進行了強度校核和穩定性校核，校核結果均符合要求。