基于貝葉斯網絡的學生成績預測

劉艷杰，李 霞

(山東理工大學 數學與統計學院, 山東 淄博 255049)

評價學校教學質量水平高低，學生成績是一項很重要的指標。雖然“以分論英雄”的時代已經過去，但是在大樣本數據下成績依然是衡量學生知識水平的一個量化標準，同時也是對學校教學質量水平的衡量。如果能夠根據高年級學生成績的關聯性對低年級學生的成績做出預測, 并且以此恰當地制定合適的教學策略，給學生發展提出合理建議, 就可以更好地提高教學質量。對此學者提出了許多方法，如吳楠等[1]基于修正的灰色模型進行了學生成績的預測；馬潔明等[2]基于相關向量機構造了學生成績預測模型；陳勇[3]基于遺傳神經網絡實現了成績預測；羅永國[4]通過改進遺傳算法實現了學生成績預測模型的構建。鑒于貝葉斯網絡的簡單可行性，本文構建貝葉斯網絡對學生成績進行預測,選取學生的7門學科成績作為樣本數據，即貝葉斯網絡里每個節點分別表示這些學科，節點之間連接的邊表示各學科成績之間的聯系。

1 貝葉斯網絡

貝葉斯網絡(Bayesian Networks,BN)[5]又稱為信度網絡，是一種結合了概率論和圖論的不確定性知識表達與推理的方法。貝葉斯網絡是一種圖形化模型，能夠表達出因果關系和相關的不確定性知識。貝葉斯網絡由有向無環圖(Directed Acyclic Graph,DAG)和條件概率表(Conditional Probability Table,CPT)兩部分構成，所以貝葉斯網絡的學習包括兩個方面：一是結構學習，即構造一個DAG，它表達了圖中各節點的因果關系；二是參數學習，即通過樣本數據估計參數的條件概率，用條件概率量化不確定性。貝葉斯網絡解決問題具有明確直觀等優點，已經成為學術界的研究熱點，在許多領域得到了廣泛應用，如模式識別、決策支持、醫療診斷、數據挖掘、傳感器融合和自動控制等領域[6-7]。

2 貝葉斯網絡模型的構建

2.1 樣本數據

由于學生成績數據不完整，本文選取了山東理工大學數學與統計學院統計學專業2015級78名學生作為研究樣本，每名學生的數學分析、高等代數、解析幾何、概率論、數理統計、描述性統計和運籌學7門學科成績作為樣本數據，即每個樣本有7個特征屬性。為便于研究,7個特征屬性分別用A、H、G、Pr、M、D、R來表示。把78個樣本的相關數據命名為數據集。數據集的具體形式見表1。

表1 學生成績數據集Tab1. Student achievement data

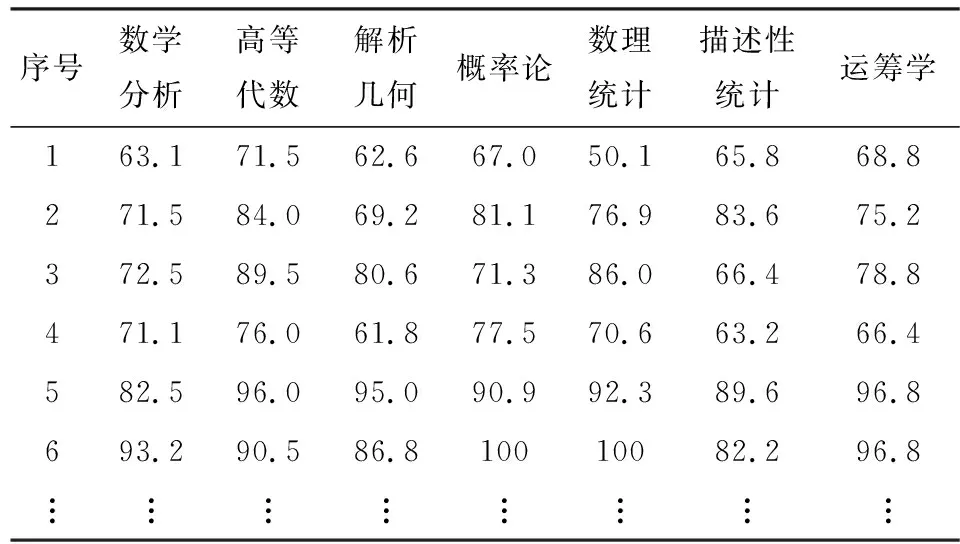
序號數學分析高等代數解析幾何概率論數理統計描述性統計運籌學163.171.562.667.050.165.868.8271.584.069.281.176.983.675.2372.589.580.671.386.066.478.8471.176.061.877.570.663.2 66.4582.596.095.090.992.389.696.8693.290.586.810010082.296.8????????

2.2 數據預處理

由于構建的貝葉斯網絡模型是基于離散數據的，所以在網絡構建之前，需要對數據進行離散化預處理。本文以80分為界值，80分到100分為優秀，80分以下為不優秀，也就是把成績分為2個等級，優秀用“1”表示，不優秀用“0”表示。數據預處理結果見表2。

2.3 貝葉斯網絡的結構學習

貝葉斯網絡結構學習方法可分為三大類：一是基于評分搜索的方法[8]，即采用評分函數(常用的評分函數有AIC，BIC等)對網絡結構進行評分，評分最高的網絡將作為最終的網絡模型[9]，這種方法主要用在蟻群算法[10-11]、 K2 算法[12]和爬山法[13]中，這種方法雖然可以得到比較精確的網絡結構，但當網絡結構比較復雜時，由于搜索空間太大，造成較低的學習效率；二是基于依賴分析(獨立性檢測)的方法[14]，這種方法主要是通過判斷變量之間的條件獨立性來確定變量對應的節點之間是否存在邊，以及邊的方向，這種方法雖然容易操作實現，但是當變量過多時，條件獨立性的判斷會呈指數增長，導致計算量過大，影響效率；三是混合方法，即將上述兩種方法融合到一起，這種方法集合了上述兩種算法的優點，成為現在研究貝葉斯網絡的主要方法[15]。本文也是在第三種方法的基礎上，用節點間的條件互信息對各節點進行條件獨立性檢測，確定貝葉斯網絡的初步結構，再利用K2算法進行全局優化，最終確定網絡結構。

表2 學生成績預處理結果
Tab.2 Student achievement data preprocessed

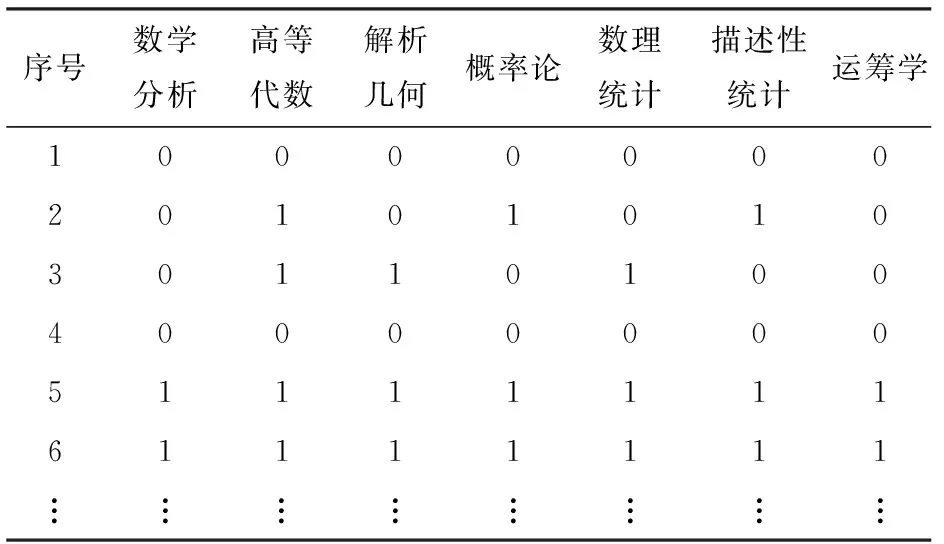
序號數學分析高等代數解析幾何概率論數理統計描述性統計運籌學1000000020101010301101004000000051111111611 11111????????

2.3.1 相關性分析

根據7個變量之間的相關性確定任意兩個變量之間是否存邊，貝葉斯網絡圖中，邊代表了兩個變量之間具有關聯性。

根據表3各學科之間的皮爾遜相關系數，發現任意變量之間的關聯系數都比較大，為了更方便區分它們之間的聯系，本文取閾值為0.65，只要兩個變量之間的相關系數比閾值大，就說明這兩個變量之間有邊的存在，再根據課程的歷史發展，按相關系數從大到小的順序給邊定向，如果在網絡中出現環，舍棄相關性比較小的兩個變量之間的邊。最終得到先驗圖，如圖1所示。

表3 學生成績相關性分析表
Tab.3 Student achievement correlation analysis table

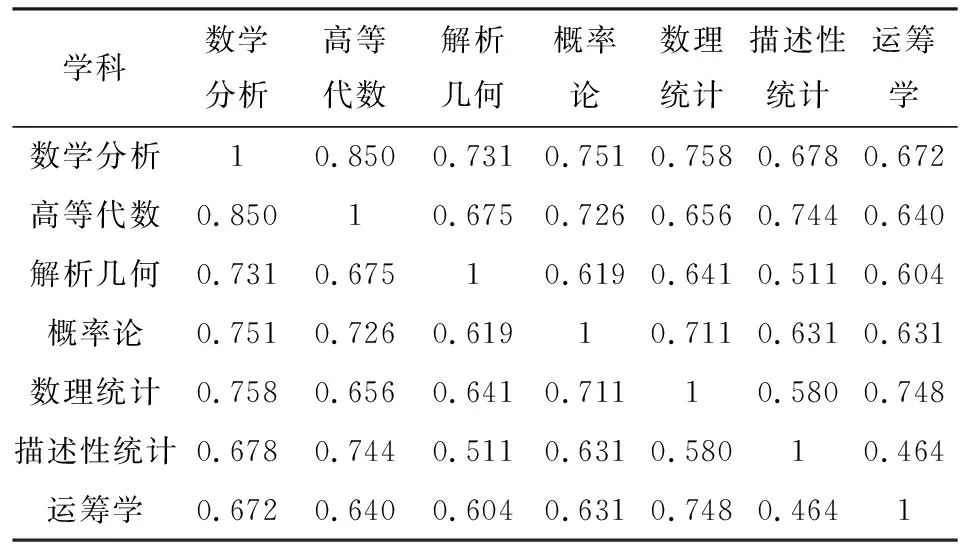
學科數學分析高等代數解析幾何概率論數理統計描述性統計運籌學數學分析10.8500.7310.7510.7580.6780.672高等代數0.85010.6750.7260.6560.7440.640解析幾何0.7310.67510.6190.6410.5110.604概率論0.7510.7260.61910.7110.6310.631數理統計0.7580.6560.6410.71110.5800.748描述性統計0.6780.7440.5110.6310.58010.464運籌學0.6720.6400.6040.6310.7480.4641

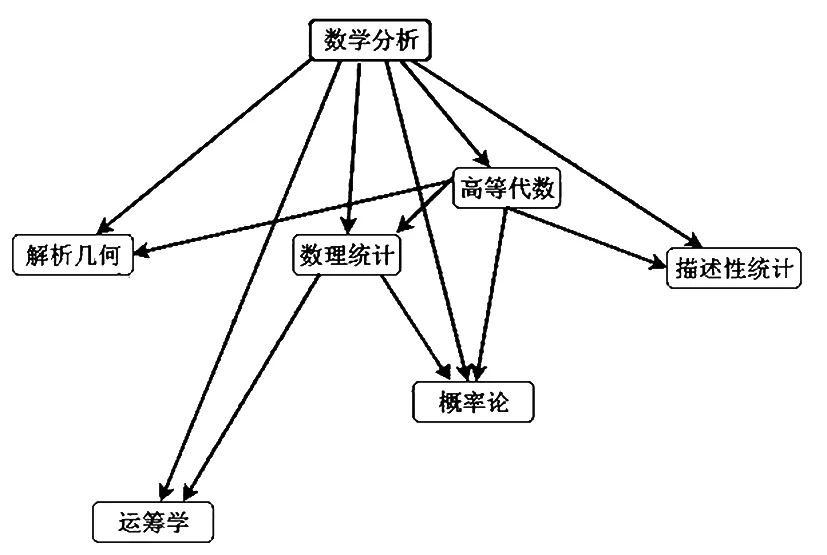
圖1 貝葉斯網絡先驗圖Fig.1 Bayesian network prior graph

2.3.2 K2算法全局搜索

K2算法由于其優越性被廣泛應用研究，但K2算法是基于節點的先驗順序進行實現的，研究早期學者根據歷史事實和專家經驗確定先驗順序，后來為了減少K2算法的主觀性，提高貝葉斯網絡建立的準確性，學者提出了許多方法，如生成最大權重樹，還有信息論的應用。本文運用變量之間的相關性和歷史經驗，建成了圖1的先驗順序后進行K2算法的搜索。K2算法的搜索結果如圖2所示。

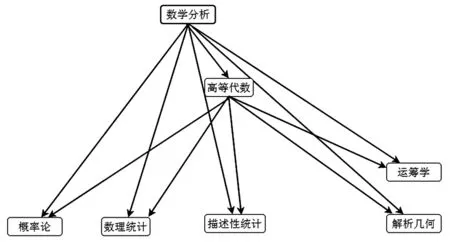
圖2 貝葉斯網絡K2算法搜索圖Fig.2 Bayesian network K2 algorithm search graph

由圖2可以很直觀地發現，數學分析和高等代數是其他5門課程的基礎，直接影響著5門學科的成績。相對之下，5門學科成績之間的相關性較弱。

2.4 貝葉斯網絡的參數學習

貝葉斯網絡的參數是變量的條件概率表(CPT)，本文利用數理統計的方法[16]建立條件概率表。根據2.3確定的貝葉斯網絡父子節點關系，依次計算出每個節點的條件概率，得到7門學科的條件概率表，分別見表4—表10。

表4 數學分析條件概率表
Tab.4 Mathematical analysis conditional probability table

P(A=0)P(A=1) 0.650.35

表5 高等代數條件概率表
Tab.5 Higher algebra conditional probability table

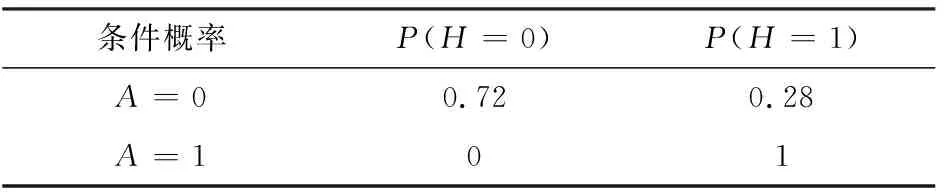
條件概率P(H=0)P(H=1)A=00.72 0.28A=101

表6 解析幾何條件概率表
Tab.6 Analytic geometry conditional probability table

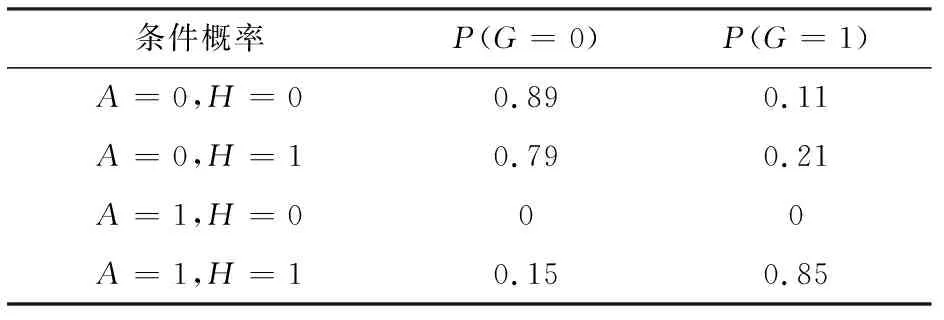
條件概率P(G=0)P(G=1)A=0,H=00.890.11A=0,H=1 0.790.21A=1,H=000A=1,H=10.150.85

表7 概率論條件概率表
Tab.7 Probability theory conditional probability table

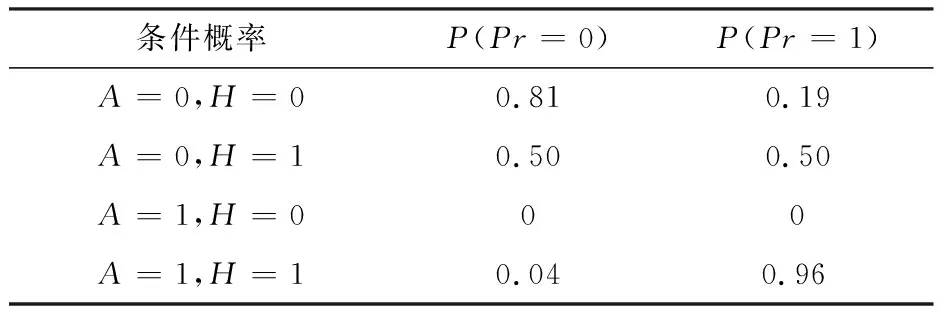
條件概率P(Pr=0)P(Pr=1)A=0,H=00.810.19A=0,H=10.500.50A=1,H=000A=1,H=10.040.96

表8 數理統計條件概率表
Tab.8 Mathematical statistics conditional probability table

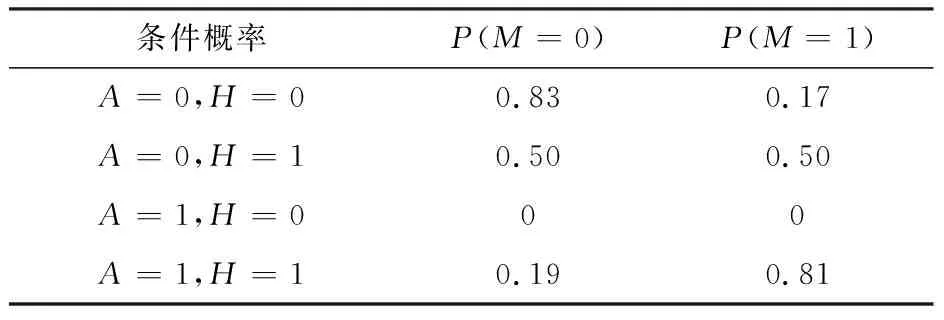
條件概率P(M=0)P(M=1)A=0,H=0 0.830.17A=0,H=10.500.50A=1,H=000A=1,H=10.190.81

表9 描述性統計條件概率表
Tab.9 Descriptive statistic conditional probability table

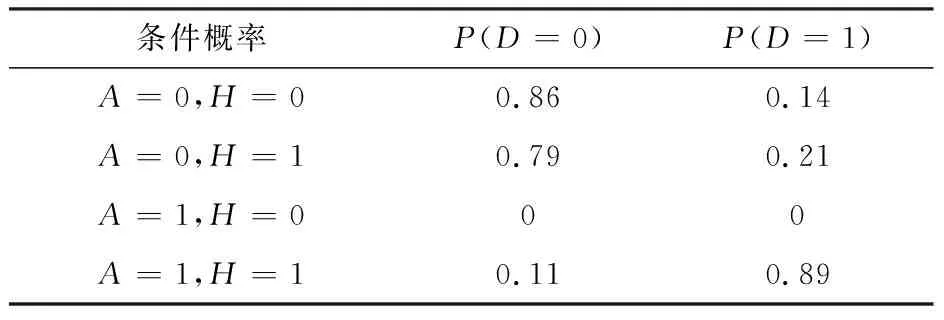
條件概率P(D=0)P(D=1)A=0,H=00.860.14A=0,H=10.790.21A=1,H=000A=1,H=10.110.89

表10 運籌學條件概率表
Tab.10 Operations research conditional probability table

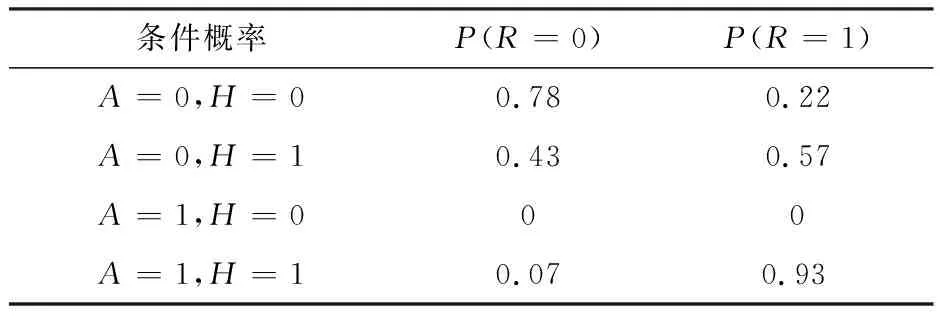
條件概率P(R=0)P(R=1)A=0,H=00.780.22A=0,H=10.430.57A=1,H=000A=1,H=10.070.93

3 貝葉斯網絡推理

貝葉斯網絡推理[17]是在得到貝葉斯網絡的情況下，根據已知結點，利用貝葉斯公式求解其他結點的條件概率，它的推理過程可以分為精確推理和近似推理。貝葉斯網絡推理主要分為4種:①預測，根據已有的證據(原因)，利用貝葉斯網絡的推理分析，計算出在該證據下結果發生的概率; ②診斷，根據已有的結果，利用貝葉斯網絡的推理分析，找到造成該結果發生的證據(原因)，并計算證據(原因)發生的概率; ③關聯分析，分析產生同一結果的不同證據(原因)之間的關聯; ④混合推理，上述幾種分析方式的結合。

本文利用聯合樹算法[18]進行預測推理。例如，如果已知一個學生的概率論成績是優秀，那么他的運籌學成績也是優秀的概率是多少呢？這個問題在貝葉斯網絡中轉化為求解P(R|Pr=1)的值，利用貝葉斯網絡推理中的聯合樹算法，得到：

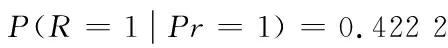
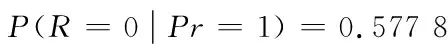
即如果一個學生的概率論成績優秀，那么他的運籌學成績優秀的概率為42%，不優秀的概率為58%。同理可以根據已有的任何一門學科成績去預測其他未知的學科成績。

4 結論

本文針對一組學生主干學科成績的樣本數據，構建了完整的貝葉斯網絡，得到以下結論：

1)從最終的貝葉斯網絡拓撲圖可以發現，相比之下，解析幾何、概率論、數理統計、描述性統計和運籌學5門課程與數學分析和高等代數的關聯性是較強的，由此可見數學分析和高等代數在整個學科體系中的重要性，所以學校在挖掘新課程的同時不能忽視對這些學科的建設。

2)在得到完整的貝葉斯網絡之后，本文利用貝葉斯網絡推理的聯合樹算法，舉例說明了成績預測的方法和過程。結果表明貝葉斯網絡成績預測是可行的，這為學校的教學管理部門提供了依據，使他們可以更好地做出管理決策。