一類具有Beddington－DeAngelis型功能反應的非自治捕食－被捕食系統的漸近行為

沈怡心， 蒲志林， 胡華書

（四川師范大學 數學與軟件科學學院，四川 成都610066）

0 引言

研究捕食－被捕食系統的動力性質是生物學家非常關注的問題，捕食－被捕食系統中一個重要的關系就是捕食者依賴于被捕食者的程度，即為捕食者的功能反應，功能反應是嚴格依賴于捕食者的．常見的功能反應類型有 Holling I－III型［1－3］、Goldstein－ Neill 型［4］、Hassell－ Varley 型［5］、Growley－Martin型［6］、比率相依型［7］及 Beddington－DeAngelis型［4，8］．

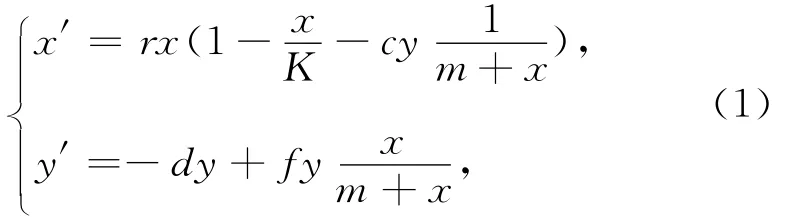
具有HollingⅡ型功能反應［2］的 Kolmogorov型的捕食－被捕食系統為其中，x代表被捕食者，y代表捕食者．該系統的不同形式引起了理論和數學生物學家的極大興趣．但是依賴于捕食者的功能反應，不能體現捕食者自身的影響，并且在生物學和生理學上也面臨著挑戰．Arditi等［7］在此基礎上提出了比率相依捕食－被捕食模型

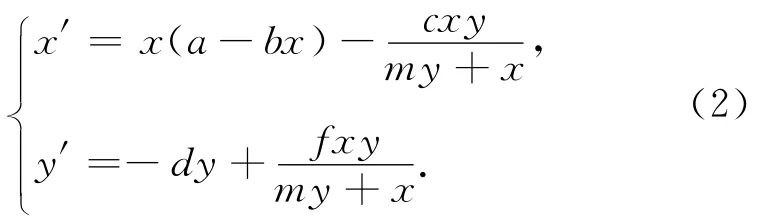
這種模型引入了捕食者的影響，更豐富地體現其中的動力學性質．但當低密度時，該系統部分性質會引起矛盾．Skalski等［2］從19個捕食與被捕食系統中得到統計數據，表明3種功能反應（Beddington－DeAngelis型、Crowley－Martin型和 Hassell－Varley型）能更好地體現捕食者依賴于捕食－被捕食系統中各個量的程度．在某些條件下Beddington－DeAngelis型功能反應能更好地體現這種關系．由 Beddington［8］和 DeAngelis等［4］分別提出的具Beddington－DeAngelis型功能反應的捕食－被捕食系統為

這個模型具有Holling II型功能反應的特點，在分母中增加的項cy體現了捕食者之間的相互影響．該模型又具有比率相依型功能反應的一些性質，并且克服了比率相依型在低密度下的缺陷．這類具有Beddington－DeAngelis型功能反應的模型被廣泛研究，其全局動力學行為得到了很好的結果［9－11］．但這些結果都是在常數環境下得到的，這在實際生活中是很少見的，大多數的自然環境都是多變的，出生率、死亡率等其他與種群數量相關的量大都依賴于時間，因此，Meng等［12］研究了具有Beddington－DeAngelis型功能反應的非自治捕食與被捕食系統

Meng等［12］對非自治系統（4）研究了t→∞時的持久性、解的全局漸近穩定性及周期解的相關性質，該非自治系統的拉回漸近性態仍有待研究．

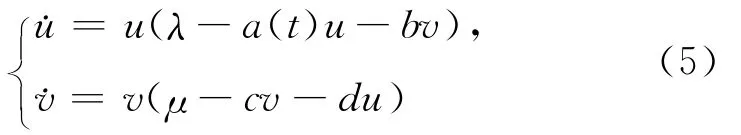
文獻［13］研究了非自治Lotka－Volterra系統的向前和拉回漸近性態．本文主要借鑒文獻［13－14］的方法，對具Beddington－DeAngelis型功能反應系統的拉回行為進行研究．

為探索具Beddington－DeAngelis型功能反應的非自治捕食與被捕食系統的拉回行為，本文將系統簡化為只有一個系數與時間t相關的方程

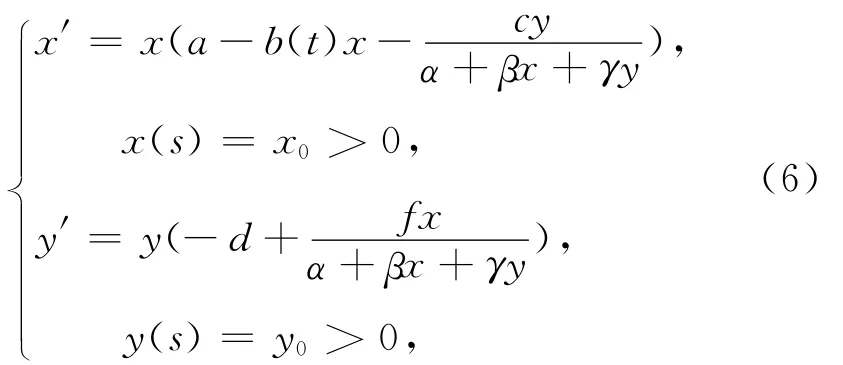
其中，a、c、d、α、β、γ都是正的常數，b（t）是 R上的有界連續函數，且恒為正．本文給出了這個方程的向前行為，并利用上下解、比較原理及logistic方程探索其拉回行為．

1 預備知識

首先介紹本文將用到的一些概念和術語等．

定義1．1［14］假設（X，d）是一個完備度量空間，S（t，s）t≥s（t，s∈R）是一個映射集族，且滿足：

（a）對所有τ≤s≤t有

S（t，s）S（s，τ）u ＝ S（t，τ）u；

（b）S（t，s）u關于t、τ和u 都是連續的；

（c）對t∈R，S（t，t）是X 中的恒等映射，則稱S（t，s）為（X，d）上的一個過程．

設（x（t，s；x0，y0），y（t，s；x0，y0））是系統（6）在初值條件x（s）＝x0，y（s）＝y0下的解，則可知S（t，s）（x0，y0）＝ （x（t，s；x0，y0），y（s，t；x0，y0））是R2上的一個過程．

定義1．2［13］X 的子集族｛K（t）｝t∈R是拉回吸引的，如果對每一個有界集D滿足

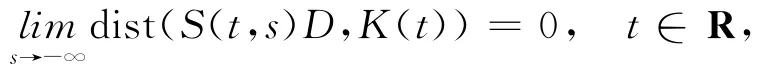
定義1．3［13］X 的子集族｛B（t）｝t∈R是關于過程S的不變集，若

定義1．4［13］緊集族是關于過程S的全局拉回吸引子，如果它是不變的、拉回吸引的，并且是最小拉回吸引（若是另一個閉的拉回吸引集族，則對t∈R有A（t）C（t））．

定理 1．5［13］存在一個全局拉回吸引子，當且僅當存在緊的拉回吸引集族

為研究系統（6）的漸近行為，給出與之相關的logistic方程及其一些有用結論．

考慮logistic方程

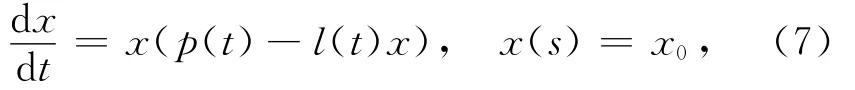
其中，p（t）＞0，l∈C0（R）．記該方程的解為θ［p（·），l（·）］（t，s；x0），經過計算可以得到

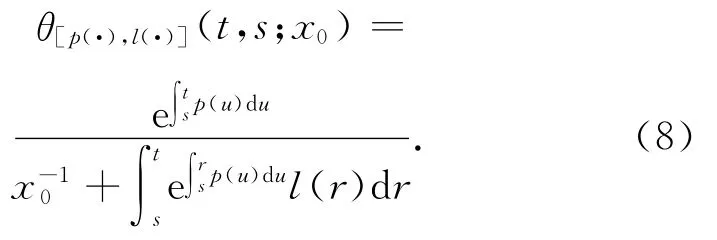
定理1．6［14］給定x（s）＝x0＞0，則存在（7）式的唯一正解θ［p，l］（t，x；x0）對t＞s是嚴格正的，并且θ［p，l］（t，x；x0）關于p 單增，關于l單減．

定理1．7［13］（7）式的解有以下性質：

（a）若p（t）→p＞0，且l（t）→0（t→∞），則θ［p，l］（t，s）→∞（t→∞）；

（b）若ps（·）→p＞0（s→－∞）（在緊子集R上一致），則存在

的解α：R→R，

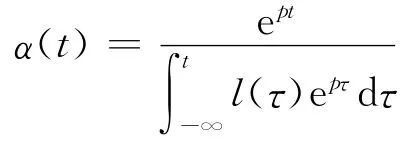
使得

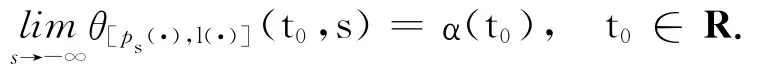
關于非自治系統（6）解的性質有如下結果．

定理1．8 給定x（s）＝x0＞0，y（s）＝y0＞0，則系統（6）存在唯一的解

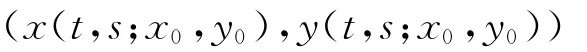
對所有t＞s嚴格為正，且

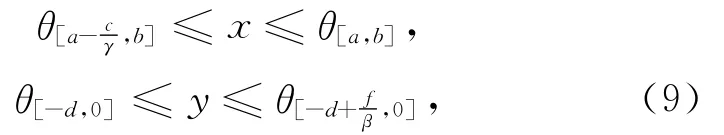
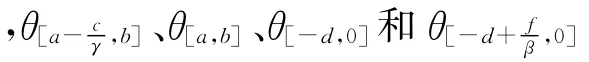
其中由（8）式給出．

證明 令

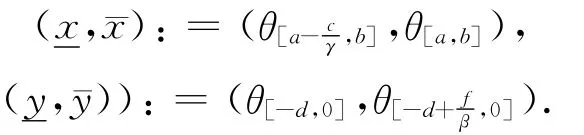
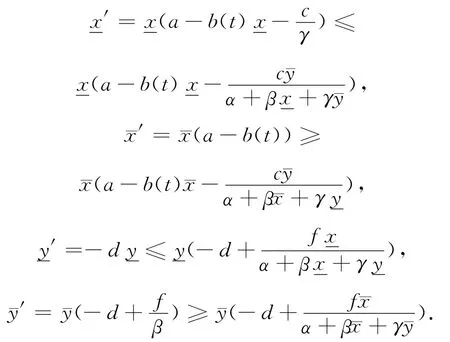
根據文獻［11，13－14］，系統的向前持久性即指對任意初始值x（s）＝x0＞0，y（s）＝y0＞0，它的解 （x（t，s；x0，y0），y（t，s；x0，y0））在某一時刻后進入到一個正的嚴格有界緊集；系統的拉回持久性則是指存在正的與時間t相關的拉回吸收集族，并且是有界的．下面給出具體的定義．

定義1．9［12］系統（6）稱為向前持久的，若存在正常數δ、Δ，0＜δ＜Δ，使得對系統（6）的所有擁有正的初始值的解滿足

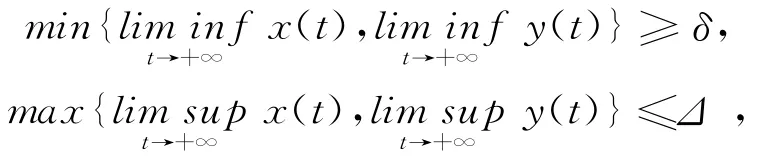
若有一個擁有正的初始值的解滿足則系統（6）是非持久的．

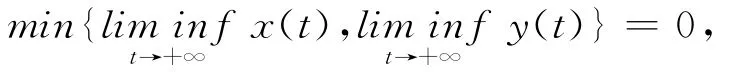
定義1．10［14］系統（6）稱為拉回持久的，若存在時間依賴集族｛U（t）｝t∈R2，滿足：

（a）U（t）吸收所有 R2中的有界集；

（b）存在ε＞0，使得對所有t∈R，滿足｜U（t）｜＞ε．

2 非自治系統的漸近性態

2．1 向前漸近行為 考慮到系統的生物因素，下面只考慮擁有正初始條件的解（x（t），y（t）），即滿足x0，y0＞0的解．對R上的有界連續函數b（t），記

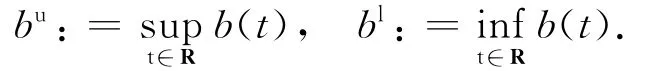
證明 對任意正的初始條件x（s）＝x0＞0，y（s）＝y0＞0，由定理1．8可知存在系統（6）唯一的解（x（t，s；x0，y0），y（t，s；x0，y0）），且滿足

其中

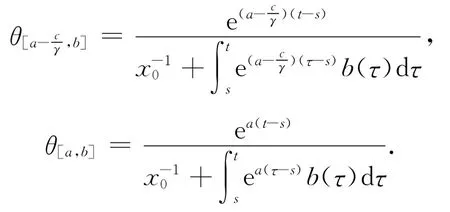
令V＝fx＋cy，則

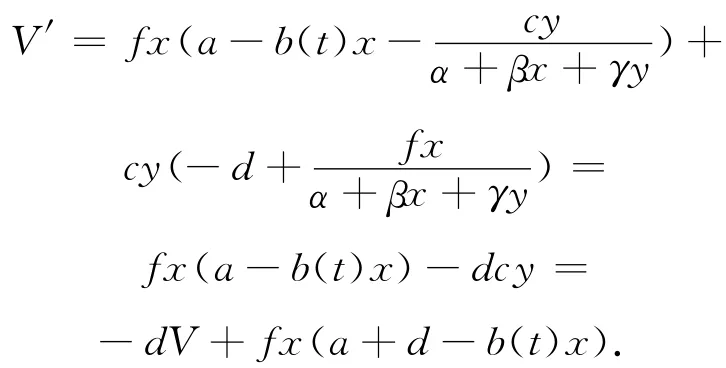
由

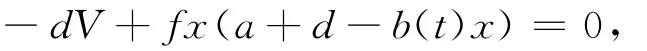
得

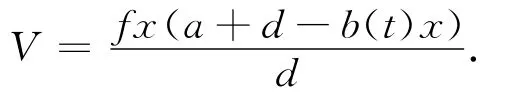
又由（10）式可得

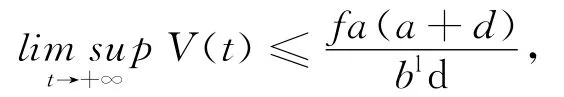
因此

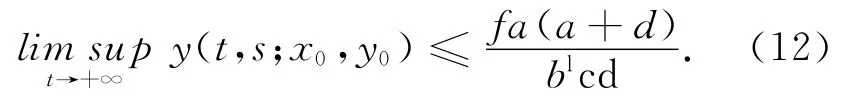
由（11）式有

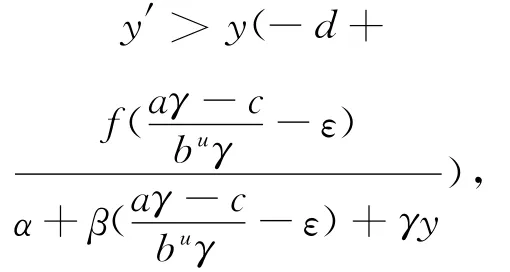
這里當t充分大時，ε＞0充分小．由

可得

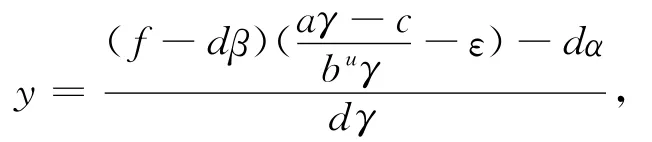
由條件可選擇充分小的ε，使

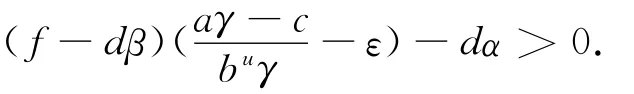
由此可推出

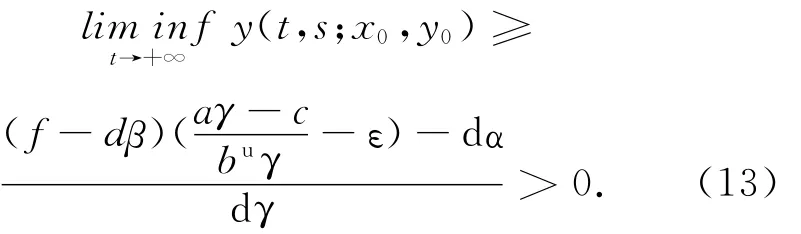
結合（10）～（13）式，系統（6）是向前持久的．

定理2．2 若βd＞f，則limy（t，s；x0，y0）＝

t→＋∞0．

證明 由定理1．8有

其中

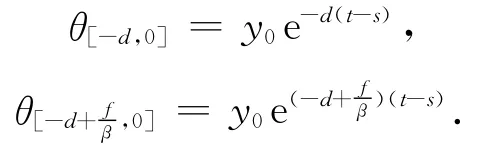
當βd＞f時

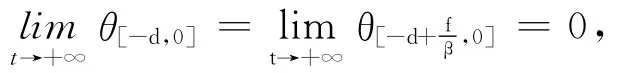
故

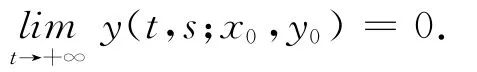
其中

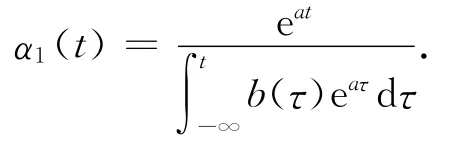
對微分方程

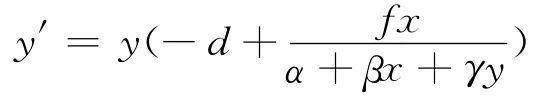
進行放縮，得到方程

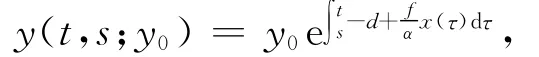
當s→－∞時，有

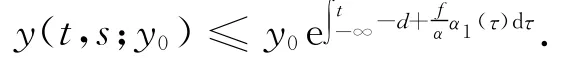
由于

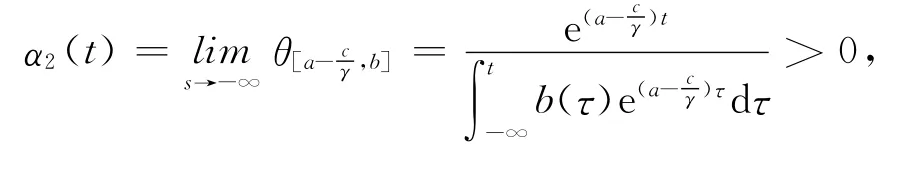
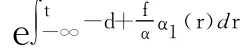
是可積的，根據函數的比較原理可知，存在β1（t）使得

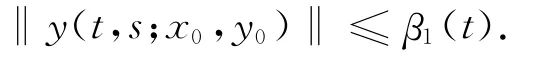
因此，在R2中存在半徑為

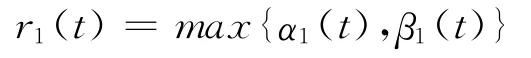
的球B（t）＝BR2（0，r1（t））是過程S（t，s）的拉回吸收集．故存在 R2中的緊的拉回集族｛B（t）｝t∈R．根據定理1．5可知存在一個全局拉回吸引子｛A（t）｝t∈R．

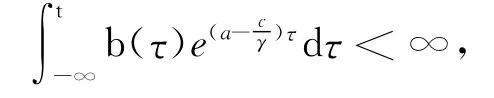
定理2．4 若且（f－dβ）α1－dα＞0，則系統（6）是拉回持久的．

其中

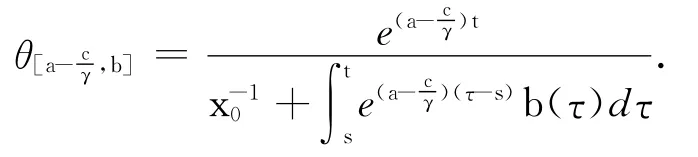
令

則有

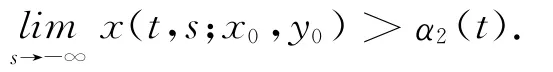
由定理2．3，存在T（t，x0，y0）∈R使得

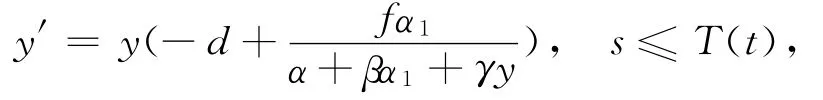
由

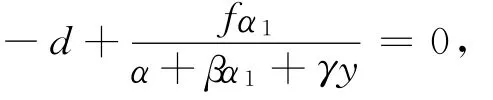
可得

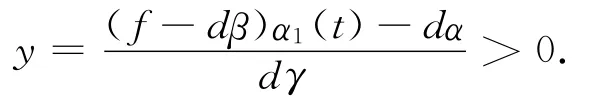
令

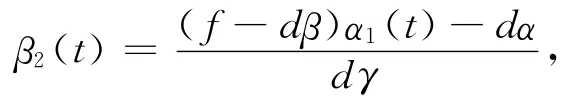
因此有

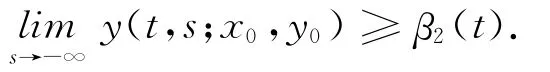
取

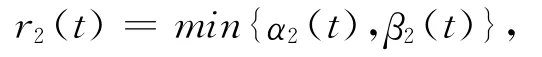
令

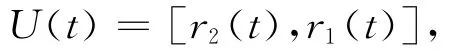
則U（t）吸收R2中的所有有界集，且滿足0，故系統（6）是拉回持久的．