網絡編碼錯誤空間與信息空間交空間的維數

劉海波， 廖群英

（四川師范大學 數學與軟件科學學院，四川 成都610066）

1 預備知識

網絡編碼（Network Coding）是由 Yeung等［1］提出，隨后由Ahlswede等［2］進一步發展起來．因為網絡編碼能顯著地提高信息的傳輸效率，所以一直是近年來的研究熱點，尤其對無錯誤發生的網絡，可參見文獻［3－10］．遺憾的是在實際網絡傳輸中會出現許多種類的錯誤．為應對這種問題，學者們提出了網絡糾錯編碼（Network Error Correction Coding），參見文獻［11－13］．事實上，網絡糾錯碼可以看作經典糾錯碼的推廣，即在經典糾錯碼里的某些界都可以推廣到網絡糾錯碼中，例如Singleton界、Hamming界和 Gilbert－Varshamov界［11－12］．達到Singleton界的線性網絡糾錯碼稱為線性網絡極大距離可分碼，簡稱為網絡MDS碼．作為一類好的網絡糾錯碼，網絡MDS碼無論在理論研究還是在現實應用中都有著重要的地位，參見文獻［14］．

在實際的網絡通訊中，需要信源通過不同的信息率傳遞不同的信息．在這種情況下，考慮到糾錯的情形，Guang等［15］構造一類變率的網絡 MDS碼，這其中涉及到對網絡MDS碼信息空間與達到最小距離的錯誤空間的交空間的維數刻化．本文將進一步刻化一般網絡糾錯碼的信息空間與達到最小距離錯誤空間的交空間的維數；在給定錯誤模式的前提下，給出網絡MDS碼信息空間與該錯誤模式所生成的錯誤空間的交空間的維數的界．

接下來介紹相關的概念與記號．通訊網絡是定義在有限非循環的有向圖G＝（V，E）上的，其中V表示點集，E表示邊集．點集V由不相交的3部分S、T以及J構成，其中S是信源節點集，T是信宿節點集，J＝V＼（S∪T）是中間節點集．

有向邊e＝（i，j）∈E表示由節點i到節點j，節點i與j稱為邊e的尾與頭，記作i＝tail（e），j＝head（e）．邊e稱為i輸出信道，j的輸入信道．給定節點i，記Out（i）為i的輸出信道集，In（i）為i的輸入信道集．

本文中考慮的是｜S｜＝1的情形，即有唯一的信源節點s．顯然信源節點s沒有輸入信道，信宿節點沒有輸出信道，為敘述方便，對信源節點s引入虛擬輸入信道．假設s單位時間內傳輸ω個域F上的元素X＝［X1X2…Xω］，則信源節點s有ω個虛擬輸入信道d′1，d′2，…，d′ω，即

令Ue為信道e上傳遞的ω－維的向量，則在信源節點s，有Ud′i＝Xi（1≤i≤ω）．在節點i∈V＼T，稱｜In（i）｜×｜Out（i）｜矩 陣 Ki＝ ［kd，e］d∈In（i），e∈Out（i）為節點i的局部編碼矩陣，其中kd，e∈F為相鄰信道（d，e）局部編碼系數．對于e∈E上傳遞的信息Ue，可以由如下的式子迭代得到易見Ue是ω個向量Xi（1≤i≤ω）的線性組合．若存在F上ω維的列向量fe，滿足Ue＝X·fe，則稱fe為信道e的全局編碼系數［6－7］，即

當有錯誤發生在信道e上時，記錯誤為Ze∈F，則信道e的輸出為珦Ue＝Ue＋Ze．特別地，將Ze視作信息稱為錯誤信息，定義｜E｜－維的錯誤向量為Z＝［Ze：e∈E］．對于信道e∈E，存在虛擬信道e′與e的尾相連，提供錯誤信息Ze．為了區分虛擬信道，稱d′i（1≤i≤ω）為虛擬信息信道，e′∈E′為虛擬錯誤信道．稱珟G＝（珟V，珟E）為G擴展網絡，其中珟V＝V，珟E＝E∪E′∪｛d′1，d′2，…，d′ω｝，E′＝｛e′：e∈E｝．令ke′，e＝1，對于d∈E／｛e｝，kd，e＝0，則G 上線性網絡編碼可以擴展到珟G上．類似地，對于e∈珟E，可以定義擴展的全局編碼系數珟fe，以及線性的網絡糾錯碼．

定義1．1［15］F上ω－維的線性網絡糾錯碼是由滿足如下條件的擴展的全局編碼系數構成：

1）當1≤i≤ω時，珟fd′i＝1d′i；當e′∈E′時，珟fe′＝1e，其中1d（d∈In（s）∪E）為（ω＋｜E｜）－維的列向量的指標函數．

2）對于其他e∈E，

其中kd，e∈F為相鄰信道（d，e）的局部編碼系數．

在信宿節點t∈T，令rowt（d）為解碼矩陣

中被指標d∈In（s）∪E所確

定｜In（t）｜－維的行向量．錯誤模式ρ為某些信道的集合，即ρE，稱錯誤信息Z＝［Ze：e∈E］匹配錯誤模式ρ是指對于e∈E／ρ，Ze＝0．對于錯誤模式ρ，以及t∈T，定義錯誤空間Δ（t，ρ）＝｛（0Z）珟Ft＝Z·Gt：Z∈ F｜E｜匹配ρ｝，以及信息空間 Φ（t）＝｛（X0）＝X·Ft：X∈Fω｝．記其中，L表示向量的集合，〈L〉由L中所有向量生成的子空間．

定義1．2［14］對于線性網絡糾錯碼，在信宿節點t∈T的最小距離定義為其中｜ρ｜記為錯誤ρ的階．

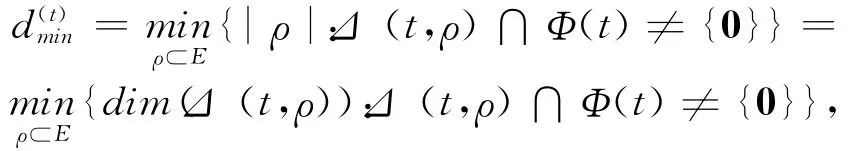
引理1．3［14］（Singleton界） 令d（t）min為線性網絡糾錯碼在信宿節點t∈T的最小距離，則其中，Ct為信源節點s與信宿節點t的最小割，ω為信息率，δt＝Ct－ω為信宿節點t的冗余．

達到這個界的網絡糾錯碼稱為網絡MDS碼．對于網絡MDS碼與達到最小距離錯誤空間的交空間的維數，Guang等［15］給出了如下刻化：

引理1．4［15］設Cω為G 上ω－維的網絡 MDS碼，則對于任意的信宿節點t以及錯誤模式ρ∈Q（t）有

2 主要結果及證明

本節給出本文的主要結果及證明，即定理2．1和2．2．定理2．1將文獻［15］中結果推廣到一般的網絡糾錯碼．在給定錯誤模式的前提下，定理2．2給出其錯誤空間與網絡MDS碼信息空間的交空間維數的界．

定理2．1 設Cω為G上ω－維網絡糾錯碼，則對于任意的信宿節點t∈T以及錯誤模式ρ∈Q（t）有

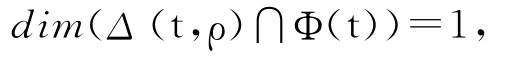
令r1，r2，…，rd為Δ （t，ρ）中d 個線性無關向量，即．假設dimΔ（ （t，ρ）∩Φ（t））≥2，令珒l1、珒l2為交空間Δ（t，ρ）∩Φ（t）中的2個線性無關的向量，則在F存在兩組不全為0的數組a1，a2，…，ad與b1，b2，…，bd滿足對于i＝1，2，…，d，ai或者bi中一定有一個為0，否則，若存在某個i（1≤i≤d）滿足ai≠0，bi≠0，即有

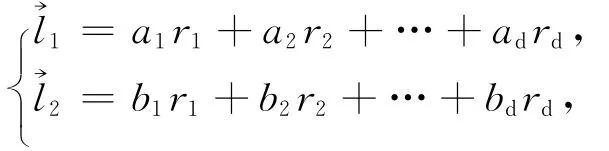
且ail2－bil1≠0．故

這也與d（t）min＝d矛盾．

綜上，對于任意的ρ∈Q（t），有

對網絡MDS碼Cω，在信宿節點t∈T定義錯誤模式的集合為

其中1≤i≤｜E｜－δt．對于任意的信宿節點t∈T以及錯誤模式ρ∈Qi（t），如下的定理2．2給出的界．

定理2．2 設Cω為G上ω－維網絡MDS碼，則對任意的信宿節點t∈T以及錯誤模式ρ∈Qi（t），有

證明 對i用數學歸納法．當i＝1時，由引理1．4即得．假設當i＝k－1（k＞1）時，結論成立．

當i＝k 時，注意到 Qk（t）＝Qk－1（t）∪ ｛ρ：則只需證明對于任意信宿節點t∈T，以及錯誤模式ρ∈Qk（t）且，滿足即可．事實上，對于任意，由（1）式有．另一方面，根據定義1．2，有因此，對于任意的有為敘述方便，記，其中．令為Δ （t，ρ）中d 個線性無關的向量，即

所以，對于1≤j≤k＋1，由于存在某些aj，1＝0，不失一般性，對于1≤c≤d，假設c）且如若不然可以調整d個向量r1，r2，…，rd的順序．對于1≤j≤c，有珒lj∈，即對于，由有

由歸納假設，知k個向量珒lj（j＝1，2，…，c），

中線性相關的，即存在不全為0的b1，…，bk∈F，滿足

等價于

這就證明了定理2．2．