反序上下解條件下二階多點邊值問題

李海艷， 王 敏

(1．四川大學錦城學院，四川成都611731; 2．成都工業學院人事處，四川成都611730)

0 引言

微分方程邊值問題在應用數學和物理學領域有著廣泛的研究．關于微分方程的邊值問題解的存在性也得到了廣大學者的關注［1－14］．尋求邊值問題解的方法非常豐富，其中上下解方法結合單調迭代技術是求解邊值問題的有力工具．單調迭代方法可以用于逆序上下解的情形，即凡是反極大值原理成立的邊值問題都可以采用這種方法，典型的有奇異邊值問題、周期邊值問題和 Neumann 問題［15－17］．

受文獻［16－17］的啟發，本文運用反序上下解方法結合單調迭代技巧和壓縮映像原理研究了如下的多點邊值問題:

n－2其中，ωi∈［0，+!)，且滿足 0 ＜ ∑i=1ωi＜ 1，(i=1，2，…，n－2)，0＜ξ1＜ξ2＜…＜ξn－2＜1，

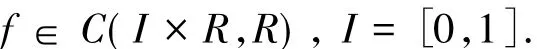
1 相關引理及其證明為了研究問題(1)，考察邊值問題

其中，φ∈C(I)，a為任意常數．本文假設:

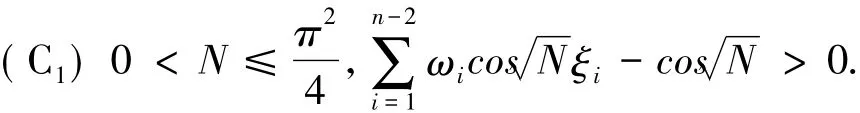
引理 1．1 邊值問題

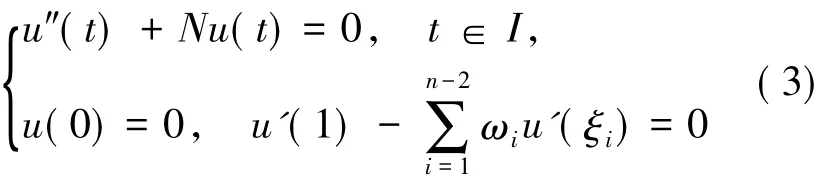
具有如下的格林函數

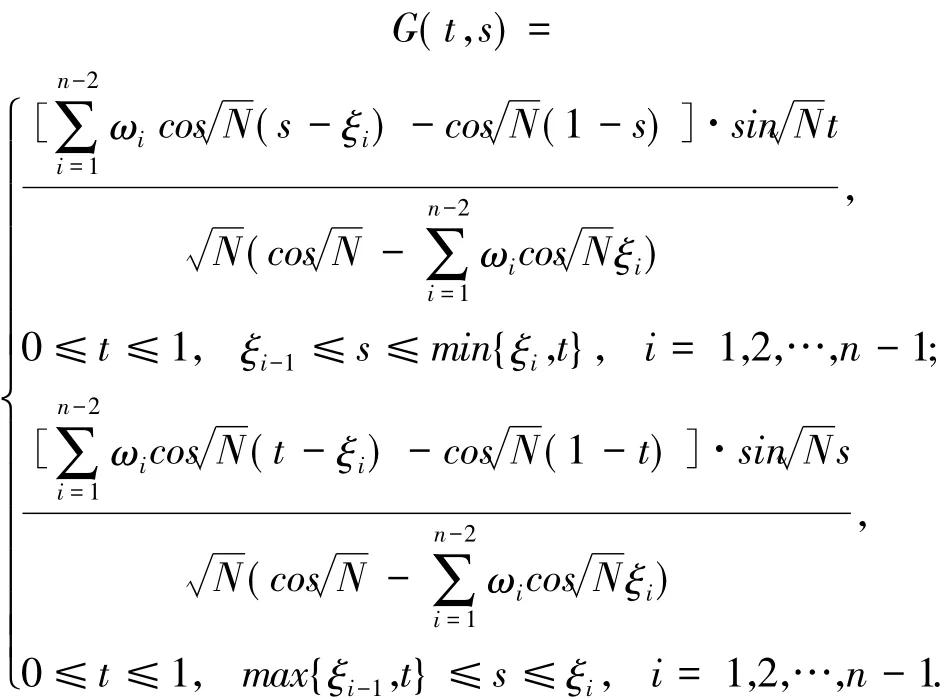
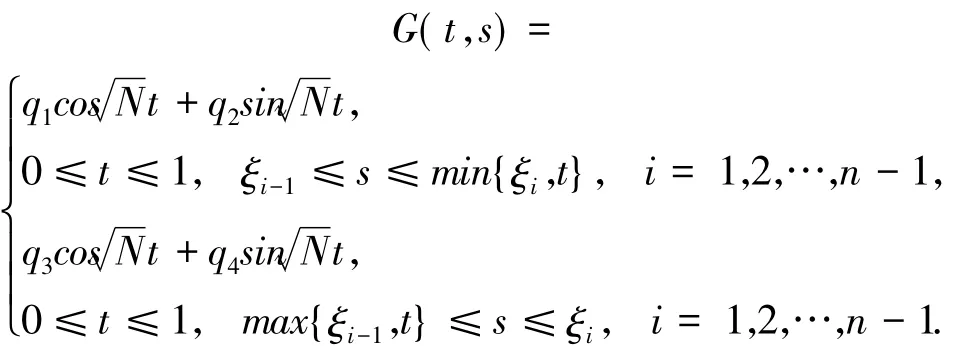
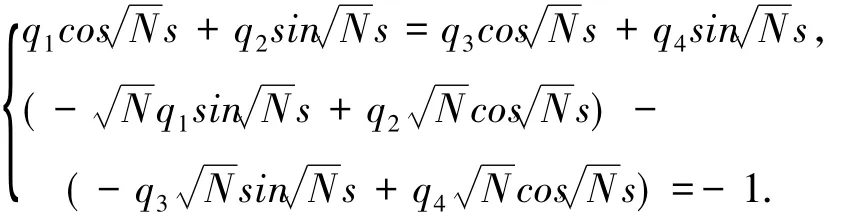
由此可得

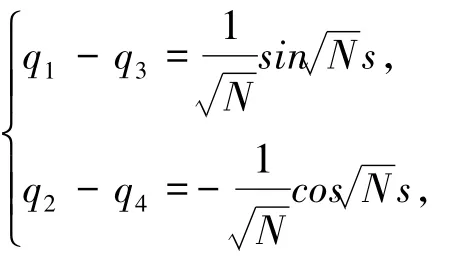
在格林函數的第一個式子中，令t=0，由邊界條件u(0)=0，可得 q1=0．

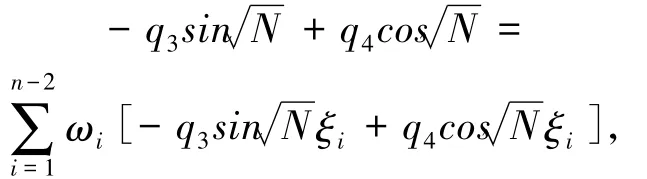
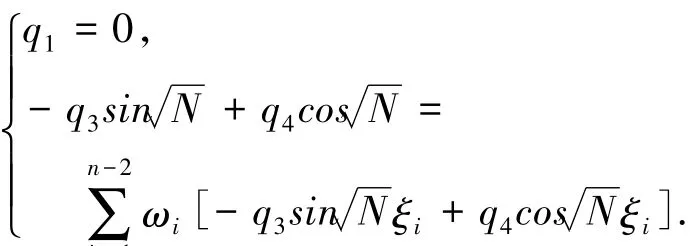
即有i=1

將上面2組等式聯立可得

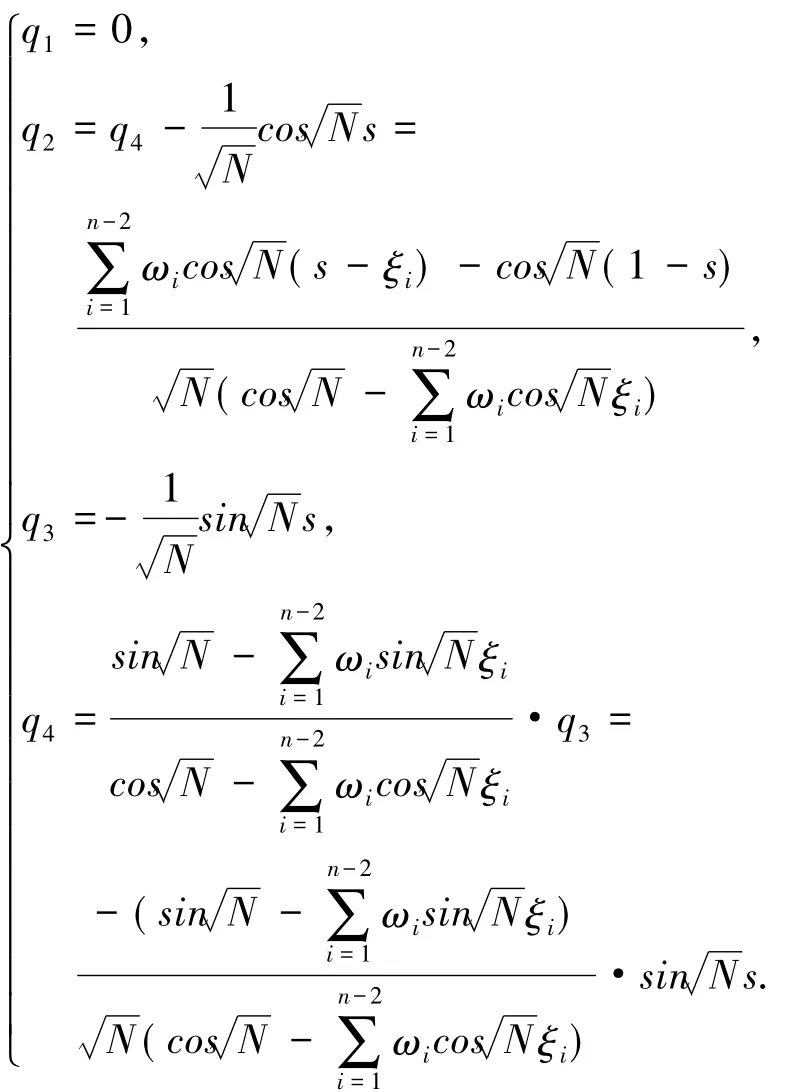
綜上，可得格林函數G(t，s)，證畢．

注1 若(C1)成立，則容易驗證對任意的t，s∈［0，1］，G(t，s)≥0，并且有

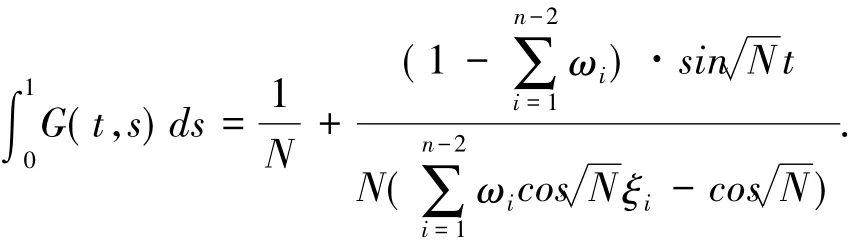
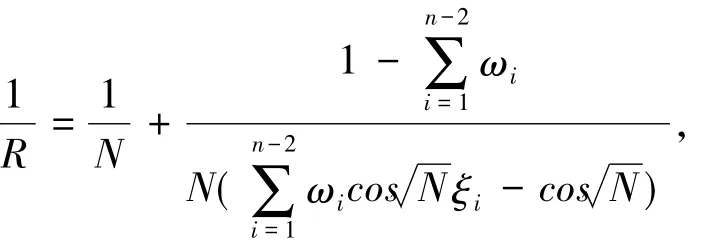
對，有

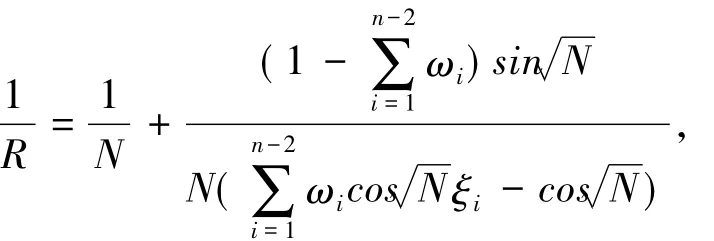
且R≥N．

引理 1．2 u∈C2(I)是邊值問題(2)的解，當且僅當u∈C(I)是下面積分方程的解．

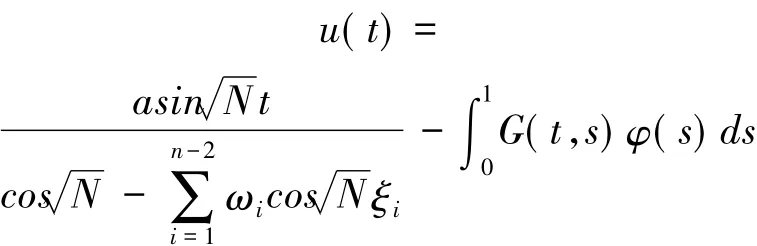
證明 假設G(t，s)是方程

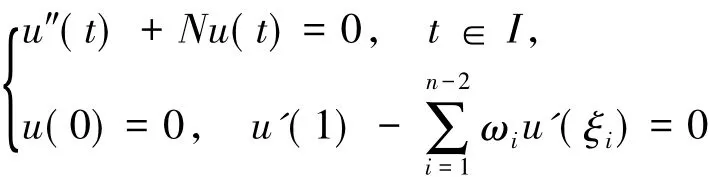
的格林函數，且u0(t)是方程

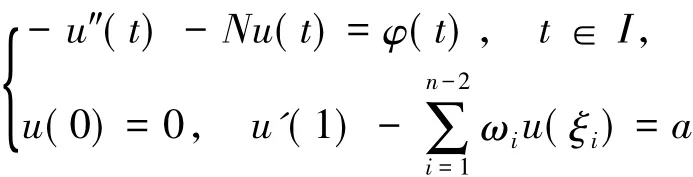
的一個解，則邊值問題(2)等價于

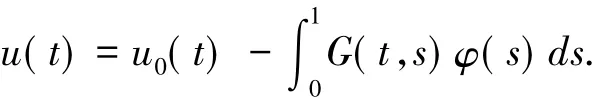
假設u0(t)=p1cost+p2s int，結 合可得

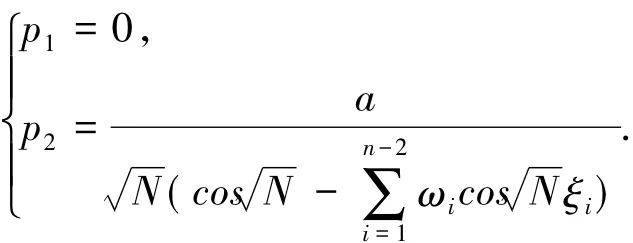
因此，邊值問題(2)等價于

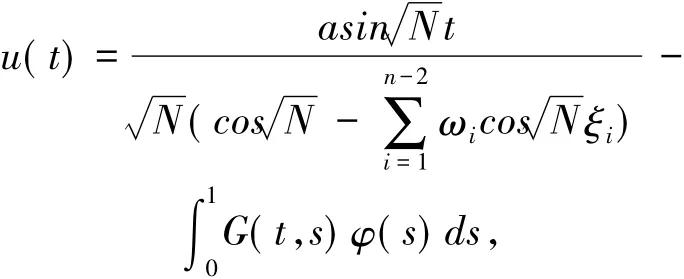
即u∈C2(I)是邊值問題(2)的解，當且僅當u∈C(I)是下面積分方程

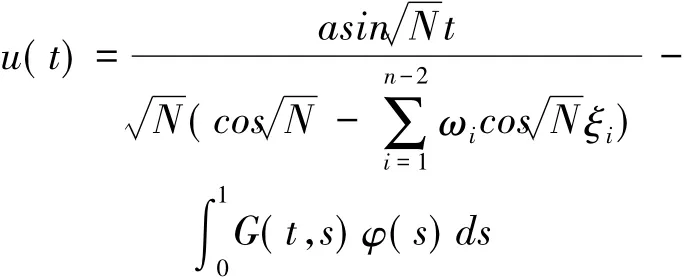
的解．證畢．

引理 1．3 假設u∈C2(I)滿足

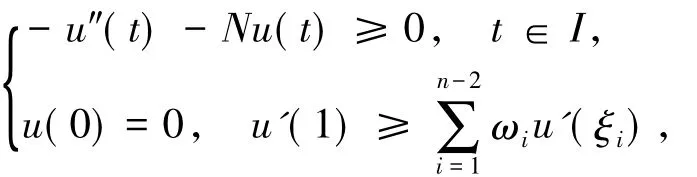
則 u(t)≤0，t∈I．

證明 令 φ(t)= －u″(t)－Nu(t)，則 φ(t)≥0，t∈I．

考慮邊值問題(2)，其中 a≥0．由引理 2．2可知，邊值問題(2)等價于

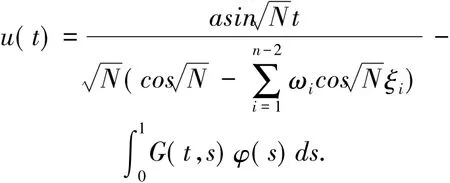
定義 1．1［18］令 E 為 Banach空間，P 為 E 中的一個錐，若存在M＞0，使當θ≤x≤y(θ為E中的零元)，恒有‖x‖≤M‖y‖，則稱P為正規錐．

引理 1．4［18］令 E為一個半序 Banach空間，{xn}E是一個單調序列且為相對緊集，則序列{xn}收斂．

引理1．5［18］令E為一個半序Banach空間，xn≤yn(n=1，2，…，n);若 xn→x*，yn→y*，有x*≤y*．

2 存在性結果

考察下面的邊值問題

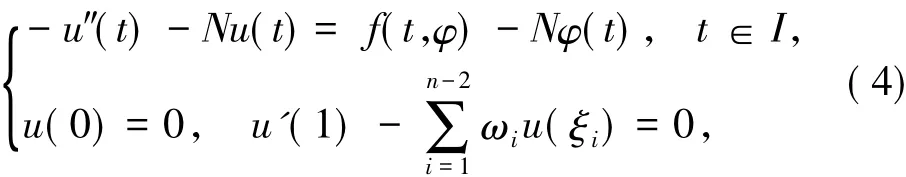
結合引理1．2，可知邊值問題(4)等價于積分方程

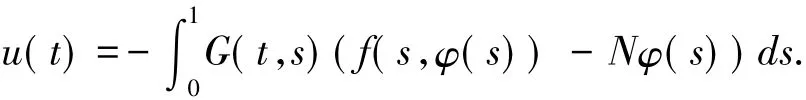
定義算子F:C(I)→C(I)有

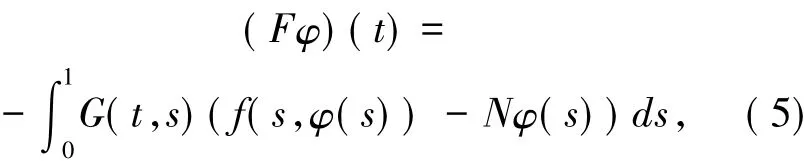
顯然算子F:C(I)→C(I)是全連續算子．

引理 2．1 u∈C2(I)是邊值問題(1)的解當且僅當u是算子F的不動點．

定義 2．1(比較定理) α0∈C2(I)稱為邊值問題(1)的一個下解，若

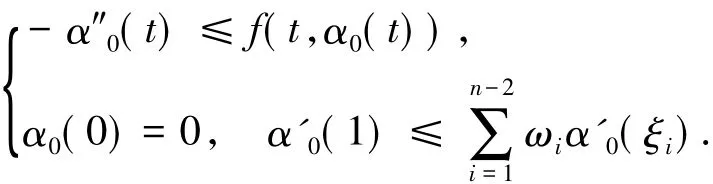
類似地，β0∈C2(I)稱為邊值問題(1)的一個上解，若

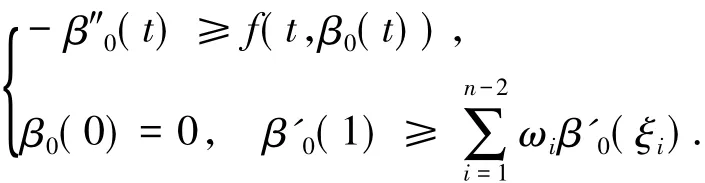
定理 2．1 假設(C1)成立，設 β0和 α0分別是邊值問題(1)的一個上解和下解，并且 β0(t)≤α0(t)(t∈I)，且 f滿足

(C2)f(t，x) － f(t，y) ≤ N(x － y)，t∈ I，β0(t) ≤y≤x≤α0(t)，則邊值問題(1)在［β0，α0］中具有最小解u*(t)和最大解u*(t)，且βn(t)→u*(t)，αn(t)→u*(t)(n→!)關于 t∈I一致，這里

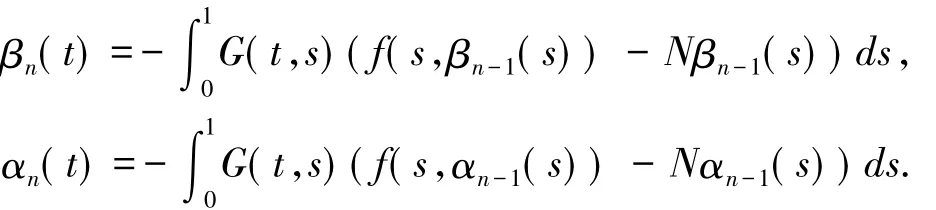
證明 根據引理2．1，只需證明算子F在［β0，α0］中有最小不動點和最大不動點．

當 β0≤u1≤u2≤α0時(即 β0(t)≤u1(t)≤u2(t)≤α0(t)，t∈I)，由算子 F 的定義有故由(C2)和注 1，有 f(s，u1(s))－Nu1(s)≥f(s，u2(s))－Nu2(s)，G(t，s)≥0，即 Fu1≤Fu2，因此 F是增算子．

下證 β0≤Fβ0，Fα0≤α0．

令 Fβ0=β1，v=β0－β1，由算子 F 的定義

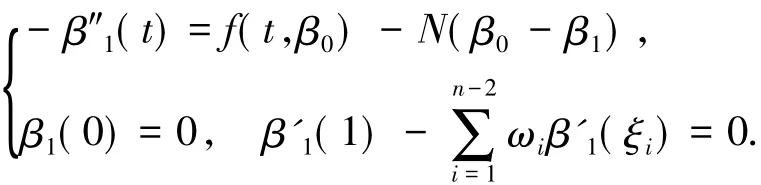
再注意到β0是上解，由上解的定義可知

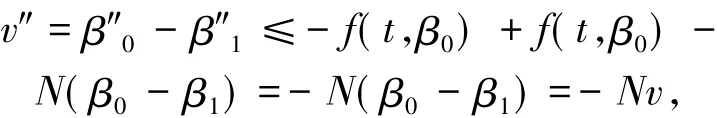
即－v″－Nv≥0．

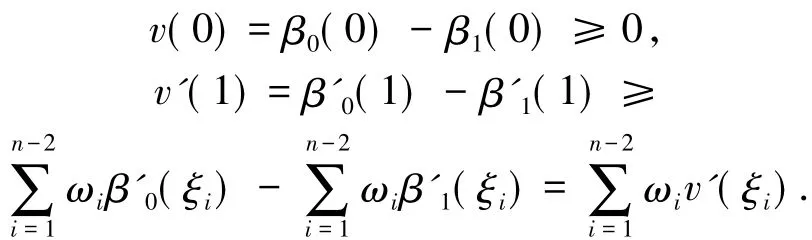
再由引理 1．3，有 v(t)≤0，即 β0－β1=β0－Fβ0≤0，從而 β0≤Fβ0．

類似地，可證 Fα0≤α0．由以上證明及(C2)可得

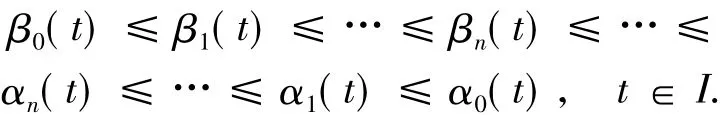
再由{βn}，{αn}F(［β0，α0］)，易知{βn}，{αn}是單調序列，且為相對緊集，由引理1．4可知存在u*，u*∈C(I)，使得 βn→u*，αn→u*(n→!)．

由 F 的連續性，u*=Fu*，u*=Fu*(n→!)，故u*、u*為F的不動點．

下證u*、u*分別是邊值問題(1)在D中的最小解和最大解．

假設 w∈［β0，α0］是 F 的不動點，則 β0≤w≤α0．由于 F 為增算子，則有 Fβ0≤Fw≤Fα0，即 β1≤w≤α1，依次可知 βn≤w≤αn．不等式兩端取極限，結合引理1．5，可得 u*≤w≤u*，即 u*、u*分別是算

3 主要結論

子F的最小不動點和最大不動點，因此，u*、u*分別是邊值問題(1)的最小解和最大解．證畢．

定理 2．2 假設(C1)和(C2)成立，且f滿足:(C3)存在常數 X且 0＜X＜N，若 R≥N，有f(t，x)－f(t，y)≥X(x－y);

(C4)存在常數X且 N－R＜X＜N，若 R＜N，有 f(t，x)－f(t，y)≥X(x－y)．

則邊值問題(1)在 C(I)∩［β0，α0］中具有唯一解．

證明 只需證明算子 F在 C(I)∩［β0，α0］中具有唯一不動點．根據假定，得

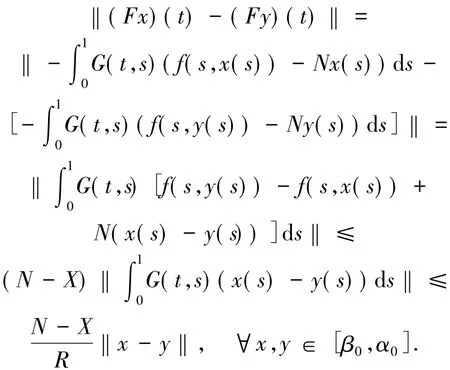
于是，由壓縮映像原理知F在C(I)∩［β0，α0］中具有唯一不動點．證畢．

本文研究反序上下解條件下二階多點邊值問題解的存在性和唯一性．根據方程的結構，定義了算子F，當算子F映序區間入序區間時，利用反序上下解方法研究該類問題不動點的存在性．引入增算子，給出單調迭代序列，證明了最大解和最小解的存在性，并運用壓縮映像原理討論解的唯一性．