一類擬周期線性哈密頓系統的有效約化性

李 佳， 朱春鵬

(徐州工程學院數學與物理科學學院，江蘇徐州221111)

假設A(t)是一個n×n矩陣，由Floquet定理知，如果A(t)是一個T周期矩陣，則x=A(t)x可以通過一個T周期變換，使其約化為常系數線性方程．Johnson等［1］進一步考慮了假設系數矩陣A(t)滿足全譜條件，則擬周期系統x=A(t)x是可約化的．所謂的約化是指存在一個擬周期非奇異變換x=φ(t)y，其中φ(t)和φ(t)－1是擬周期且有界的，使得x=A(t)x變為y=By，其中B是常數矩陣．Jorba等［2］考慮了線性擬周期方程x=(A+εQ(t))x，其中x∈Rn，常數矩陣A是有不同的特征值．他們得到在非共振條件和非退化條件下，存在一個非空Cantor集E，使得當 ε∈E 時，方程是可約化的．Xu［3］把上面的結論推廣到了有相同特征值的情況．Jorba等［4］考慮了非線性擬周期系統x=(A+εQ(t))x+εg(t)+h(x，t)，x∈Rn，其中 A有 n個不同的非零特征值．在非共振條件和非退化條件下，他們得到了ε∈E時，非線性系統是可約化的．Li等［5］進一步推廣到了有重特征值的情況．但是，上面的文獻只考慮了解析系統的約化性．近來，Li等［6］考慮了矩陣A不同特征值情況下，有限光滑擬周期系統x=(A+εQ(t))x的可約化性．雖然這樣，上述文獻的約化性都是約化到常系數矩陣的．不同于約化到常系數矩陣的情況，Jorba等［7］考慮了擬周期方程x=(A+εQ(t))x的有效約化性，其中常數矩陣A是有不同的特征值．他們得到在只有非共振條件，沒有非退化條件的情況下，對于所有的參數ε，通過一個擬周期變換，系統可以約化為y=(A*(ε)+εR*(t，ε))y，其中R*關于ε是指數小的．最近，Li等［8］進一步推廣到了有不同特征值的擬周期線性哈密頓系統的有效約化性．通過構造一個辛映射，使得這個有效約化保持了哈密頓結構．

受文獻［7－8］的啟發，本文把文獻［8］的結果推廣到有重特征值的情況．

定義 1 如果 f(t)=F(ω1t，ω2t，…，ωrt)，其中F(θ1，θ2，…，θr)對于所有變量都是 2π 周期的，且θi=ωit，i=1，2，…，r，則稱函數 f是頻率為 ω=(ω1，ω2，…，ωr)的擬周期函數．

如果 F(θ)，θ=(θ1，θ2，…，θr)在 Dρ={θ∈Cr‖Im θi|≤ρ，i=1，2，…，r}上解析，則稱 f(t)在 Dρ上是解析擬周期的．記f(t)在Dρ上的最大值范數為‖f‖ρ=sup |F(θ)|．

θ∈Dρ

定義 2 如果所有的 qij(t)(i，j=1，2，…，n)在Dρ上是解析擬周期的，則稱矩陣函數 Q(t)=(qij(t))1≤i，j≤n在 Dρ上是解析擬周期的．

1 主要結論

定理1 考慮哈密頓系統

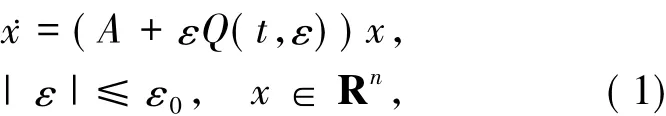
假設 A=diag(λ1Ir1，λ2Ir2，……，λlIrl)，其中 Id是 d階單位矩陣，r1+r2+…+rl=n，i≠j時，λi≠λj．假設 Q(t，ε)在 Dρ上是頻率為 ω=(ω1，ω2，…，ωr)的解析擬周期矩陣，并且關于ε連續．假設下面的條件成立．

假設 1(非共振條件) λ=(λ1，λ2，…，λn)和ω=(ω1，ω2，…，ωr)滿足

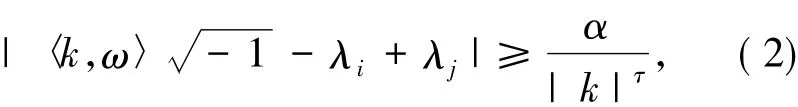
其中，k∈Zr{0}，τ＞r－1，α＞0 是一個小常數．

假設 2 記 Q(θ)=(Dij)1≤i，j≤l，其中 Dkk是 rk階矩陣，1≤k≤l．定義 D=diag(D11，D22，…，Dll)．令［D］是D關于 t的平均．假設［Dii］的特征值為 δ1i，…，δrii，它們滿足

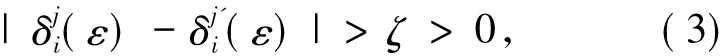
其中，j≠j'，i=1，2，…，l，|ε|≤ε0，ζ是常數．

則對于所有的|ε|≤ε*≤ε0，存在一個擬周期辛變換 x=φ(t，ε)y，其中 φ(t，ε)在 Dρ上是頻率為ω的解析擬周期矩陣，使得(1)式變為哈密頓系統

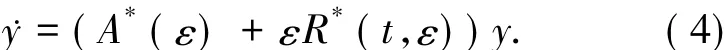
此外，有以下結論成立:

1)A*(ε)是常數矩陣，滿足‖A*－A‖≤c1ε，其中c1＞0是常數;

2)R*(t，ε)在 Dρ上是頻率為 ω=(ω1，ω2，…，ωr)的 解 析 擬 周 期 矩 陣，并 且 ‖R*‖ρ－δ≤是常數．

注 1 一般來說，Q(t，ε)依賴于 ε．下面為了簡單起見，有時省略Q(t，ε)中的參數ε．

2 定理1的證明

事實上，本文重特征值的情況主要影響文獻［8］的第一步 KAM迭代．因此，首先給出第一步KAM迭代，而以后的KAM迭代變為不同特征值的情況，完全類似于文獻［8］．

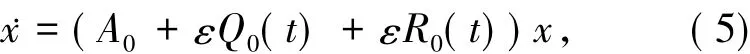
其中，A=A+ε［D］，Q=(Q－［D］)M，R=

000

(Q－［D］)≥M．類似于文獻［8］，做辛變換 x=eεP0y，其中哈密頓矩陣P0將在下面定義，則方程(5)變為

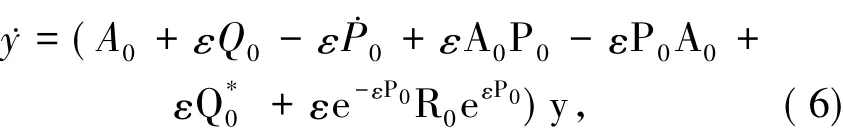
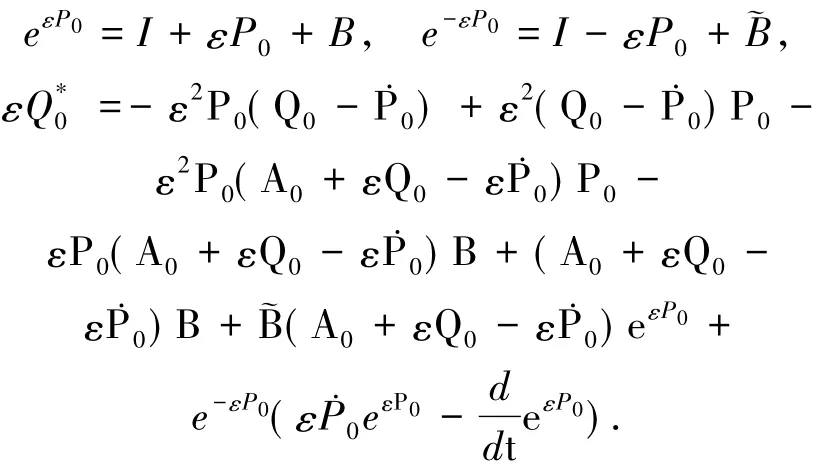
其中此時，希望系統(6)中Q0－P0+A0P0－P0A0=0，等價于解方程

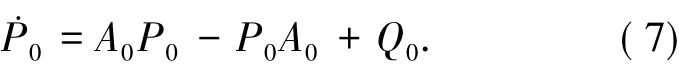
由假設2，即A0的特征值互不相同，于是，存在可逆矩陣 S，使得 珔A0=S－1A0S=diag(λ01，λ02，…，λ0n)，其中 A0的特征值為{λi+εδji}，i=1，2，…，l，j=1，2，…，ri．令S－1P0S=P珔0，S－1Q0S=Q珚0．于是，解方程(7)實際上變為解方程把P珔0和Q珚0展開為傅里葉級數 珚Q0=其中．如果并且當λ0i'和λ0j'分別是A0中不同的小分塊矩陣的特征值時，|λ+i'－λ+j'|≥δ0，其中，M(ε)=?是常數，則通過比較

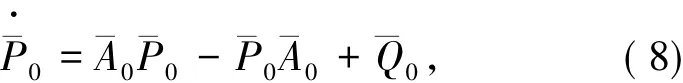
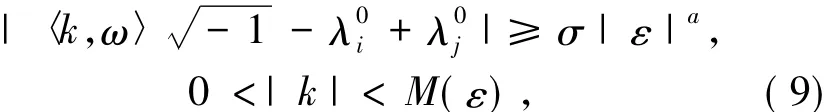
(8)式的傅里葉系數，有P珔0ij=0，(i，j)為矩陣 D 中小分塊矩陣Dmm中的元素的坐標，1≤m≤l;其他，P珔kij=于是，方程(7)可解．另外，由于A0和Q0是哈密頓矩陣，于是P0也是哈密頓矩陣．具體證明見文獻［8］中的引理2．2．此時，哈密頓系統(6)變為令Q0*=(D*ij)1≤i，j≤l，其中，D*kk是 rk階矩陣，1≤k≤l．定義 D*0=diag(D*11，D*22，…，D*ll)．由于Q0*是哈密頓矩陣，于是D*0也是哈密頓矩陣．哈密頓系統(10)變為

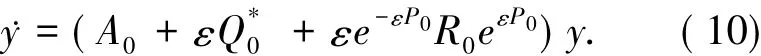
其中，A1=A0+ε［D0*］，Q珟0=Q*0－［D*0］，Q1=Q珟M0(ε)，

R1=Q珟≥0

M(ε)+e－εP0R0eεP0．A1、Q1、R1都為哈密頓矩陣．下面證明非共振條件(9)成立．當k∈Zr，0＜|k|時，由定理的假設1，有

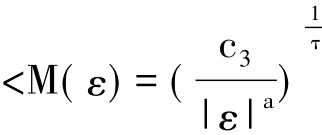
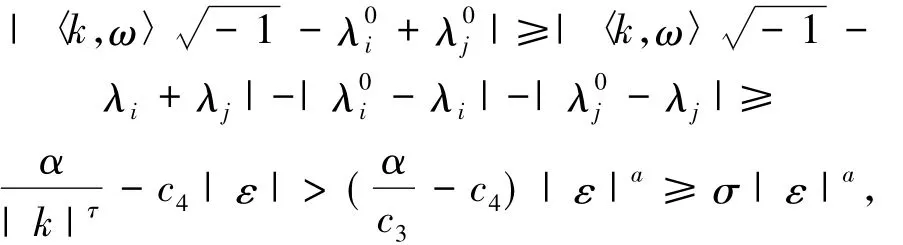
是常數．

對于哈密頓系統(11)，A1的特征值互不相同．這是因為，由文獻［8］的(3．14)式，得到 Q*0=O(ε1－2a)，a∈(0，)．再由假設 2及(11)式，得到A1的特征值互不相同．事實上，對于下面每一步KAM迭代中的Ad，d∈Ν，它們分別都有不同的特征值．下面的證明完全類似于文獻［8］，為了簡單起見，此略．

致謝徐州工程學院科研項目(XKY2016214、XKY2016215和XKY2017113)對本文給予了資助，謹致謝意．