CNG公交車高壓供氣管路共振隱患防控技術

王意東 何太碧 張新巖 ,2 王 艷

1.西華大學汽車與交通學院 2.吉利集團動力總成研究院 3.成都市技師學院

0 引言

高壓供氣管路作為壓縮天然氣（CNG）公交車燃氣供給系統的重要組成部分，在車輛行駛過程中管路會受到各種振動，其激勵源主要有發動機機械振動、管路內部天然氣沖擊以及路面不平引起的車身振動[1]。當上述激勵頻率和管路自身的固有頻率接近時將導致耦合共振，不僅降低高壓管路系統構件的疲勞壽命及可靠性，帶來安全隱患，而且還影響整車的噪聲、振動與聲振粗糙度（Noise Vibration Harshness，NVH）性能，使乘坐舒適性變差。目前，國內針對CNG公交車高壓管路布局的技術標準和工藝規范較少，針對CNG汽車高壓管路振動的優化研究更是處于空白。從現有文獻來看，專家學者對CNG汽車高壓管路的研究都集中在高壓管路內部流場特性及管路結構對流場特性的影響規律方面[2-3]。鑒于此，筆者將對高壓管路的振動屬性進行分析，探究提高高壓管路可靠性、安全性及改善高壓管路NVH特性的優化方案，以期為實踐提供更多理論指導。

1 模態分析

CNG公交車高壓管路是連接氣瓶到減壓器之間的供氣管路[4]。本文所述型號CNG公交車，其氣瓶組位于公交車后車門（下客門）上方車頂處，管路為壁厚1 mm、外徑為8 mm的不銹鋼管，該鋼管泊松比為 0.29，彈性模量為 19.3 GPa，密度為 8 030 kg/m3。管路實際走向從氣瓶組的管路匯合處開始，平行于車頂向后布置到后車門前框，然后垂直向下直達車底板平面下方，再沿車底板梁框架到達減壓器，管路總長10.9 m，沿實際走向從氣瓶組到減壓閥共轉彎10次，分為11個小段。構建有限元三維模型時，為便于計算和收斂，需將供氣系統上的部分零部件的安裝特點及布局進行簡化處理。其中，從力學特征上看，可將氣門閥、三通閥、過流保護閥以及減壓器處理成個固定約束，可等同于固定供氣管路的作用。該CNG公交車沿高壓供氣管路布置了13個“U”形固定管夾，通過螺栓將高壓管路固定在底盤上，約束強度足夠，在建模時，可將這13個固定管夾處理成貼合在高壓供氣管路上的光滑圓柱體，該圓柱體質量和尺寸等效于原“U”形管夾[5]。管路有限元模型中的走向、長度均按以上實際布局建立，各固定點處約束的邊界條件設置為全自由度的固定約束。

論文所研究的CNG公交車采用了六缸四沖程發動機，其額定轉速及怠速分別為2 200 r/min、600 r/min，根據汽車理論計算可得[6]，該發動機激勵頻率范圍為30～110 Hz，這也是文章重點分析的頻率范圍。

模態分析旨在為系統的振動特性及動力學優化設計提供理論依據[7-8]。論文所關注的是管路安裝在汽車上的預應力條件下低階模態頻率和振型，因此，對管路有限元模型設定為工作環境下的全自由度的固定約束。

按照上述高壓管路實際工作結構及邊界條件特點對其進行有限元建模，使用ANSYS Workbench軟件中的Model模塊進行模態分析。表1為高壓供氣管路的前10階模態頻率，圖1為與發動機怠速激勵頻率相接近的第3階固有頻率對應的振型圖，其振型最大位移為117.2 mm，發生在管路左起第6段部位；圖2為和發動機常用轉速頻率相接近的第6階固有頻率對應的振型圖，其振型最大位移為141.8 mm，發生在管路左起第4、5段部位。

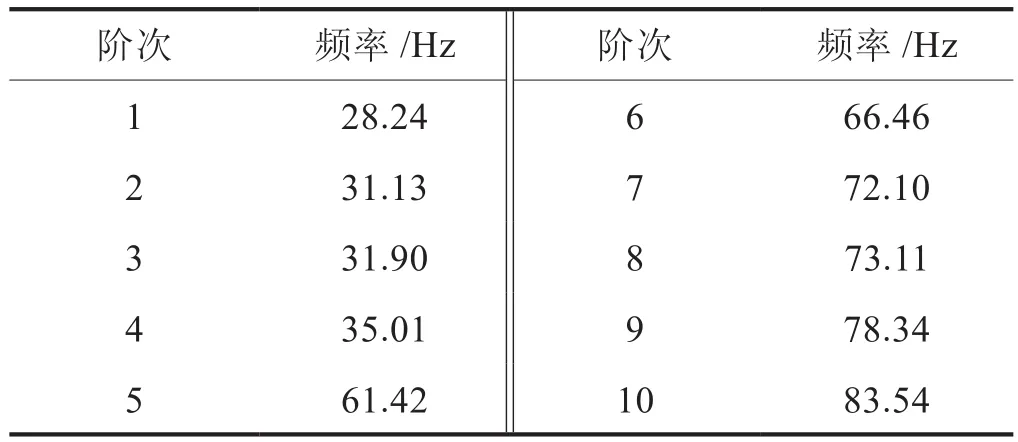
表1 高壓管路模態計算值表

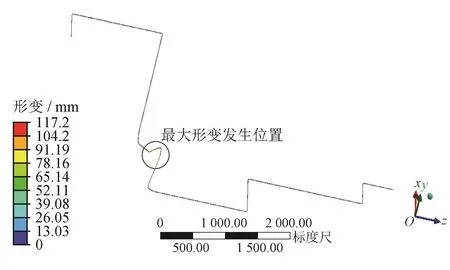
圖1 第3階約束模態振型圖

圖2 第6階約束模態振型圖

根據模態分析結果可知，原高壓供氣管路的10個階次固有頻率中有9個值分布在發動機各工況工作激勵頻率范圍內，高壓管路發生共振的可能性較大，會影響高壓管路的可靠性和安全性。如管路的第2、3、6階次的頻率分別與發動機怠速工況頻率、常用工況轉速頻率接近，容易導致耦合共振，造成管路疲勞損壞，影響其使用穩定性。

根據本文參考文獻[9]，公交車的行駛路況以城市C級公路為主，其常用車速下的激勵頻率小于30 Hz，且經過車輪及懸架的減震作用后路面激振頻率將進一步減小。對比上述高壓供氣管路的計算模態結果可知，路面不平度產生的隨機振動激勵頻率在管路的固有頻率范圍之外，不存在共振可能。因此，論文主要分析發動機怠速及常用工況轉速時的振動現象，以及高壓管路約束位置的優化方案。

2 約束位置優化

在管路所承受的內外部振動激勵無法改變的條件下，為了避免其疲勞損壞，增強管路的使用穩定性，改善NVH性能，可通過研究管路的約束、結構（內徑、壁厚、走向）的變化對固有頻率的影響規律，從而得到一個合適的改進方案。

對于高壓管路來說，管道內徑會直接影響到供氣流場，管路走向受整車實際結構約束，可調性很小，管路壁厚的調整涉及到整個管路的更換及其與車身的再次匹配。

根據高壓管路模態分析結果可知，原管路系統的約束點位置與模態振型的節點位置存在較大差異，布局不夠合理。基于以上分析，兼顧到優化方案的經濟性、可行性原則，以管路約束點位置作為研究對象，研究其優化方案。

2.1 平均驅動自由度理論

CNG公交車高壓管路的振動激勵源主要來自發動機運轉時的振動激勵，其他激勵源（如路面、流暢等）影響極小，可將此系統看作是單點激勵下的多自由度振動系統，根據模態理論，測試點l與激勵點p之間的頻率響應函數Hlp(ω)為[10]：

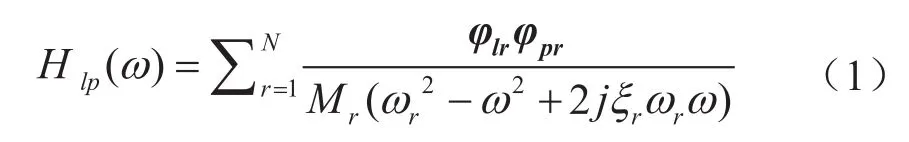
式中φlr表示第l個測試點的第r個模態向量；φpr表示第p個激勵點的第r個模態向量；ωr表示模態頻率，Hz；Mr表示模態質量；ω表示激勵頻率，Hz；ξr表示模態阻尼比。

當外部激勵頻率ω接近結構本身ωr的時，可將式（1）簡化為：

在線性系統中，位移響應幅值X(ω)與成正比，即

進行歸一化處理，若各階阻尼近似相等，則

第j個自由度的平均驅動自由度位移（ADDOFD）為：

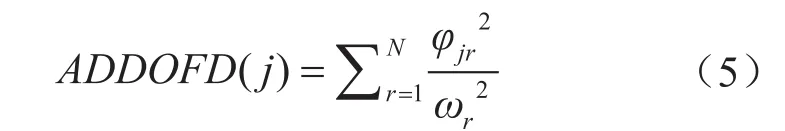
各階次固有頻率的共同作用決定了系統的實際振型，即最終的模態振型是由不同權重的各階次固有頻率共同構成的結果[11-12]。本文中，通過管路的模態分析可得到各階次振型下的位移值，然后將其按各階次固有頻率的權重進行求和，最后運用式（5）便可得出每個測試點的平均驅動自由度位移值。

2.2 確定各階次頻率權重

2.2.1 確定層次結構

發動機不同轉速激勵對高壓管路將產生不同的振動響應。鑒于此，本層次評價體系中，目標層為“高壓管路振動傳遞綜合評價”， 準則層為發動機“常用轉速”及“中高轉速”，方案層為各階次頻率。CNG公交車實際工況中，高壓管路各階次振動特性均不同，由此便可確定準則層各階次模態頻率的權重。各階模態頻率層次結構如圖3所示。

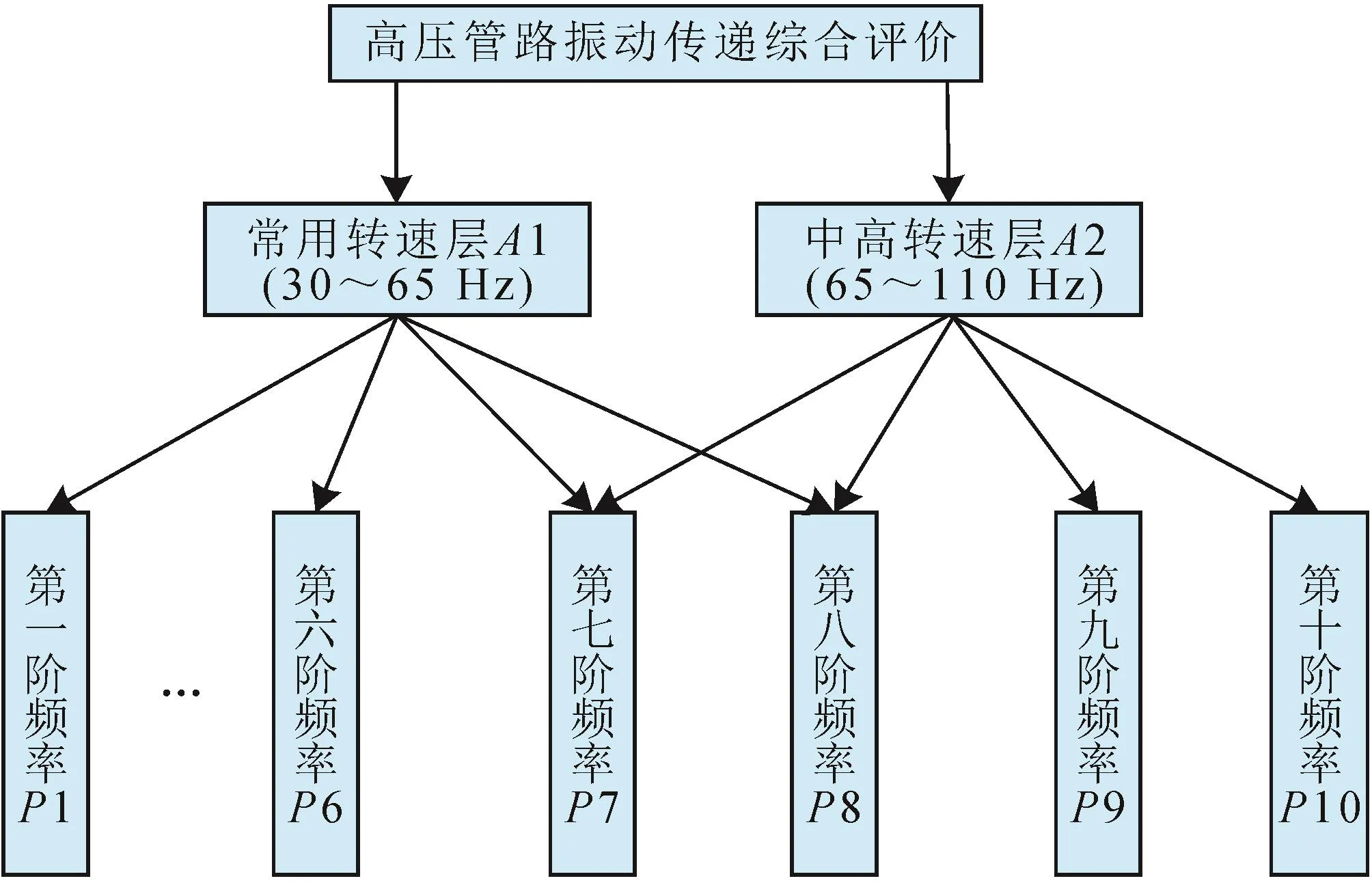
圖3 各階模態頻率層次結構圖

2.2.2 建立判斷矩陣

建立各階模態頻率層次結構后，還需比較兩個準則層（A1、A2）對目標層（X）的重要程度，再分別確定第1到第10階頻率對準確層的重要程度，基本方法是讓每一個因素分別與其他因素（含自身）一一比較。如當有n個因素時，一一比較后便可形成一個n×n的判斷矩陣，判斷矩陣是否有效還需通過一致性檢驗，當一致性檢驗率CR＜0.1，則該判斷矩陣通過一致性檢驗，可采用。

基于上述分析，并利用9級標度準則[13]，便可分別得到X—A層、A1—P層、A2—P層的判斷矩陣。

X—A層判斷矩陣及CR值為：

A1—P層判斷矩陣及CR值為：

A2—P層判斷矩陣及CR值為：

2.2.3 確定總的權重

根據2.2.2中的判斷矩陣，利用權重求解算法，便可得到各階頻率對目標層（高壓管路振動傳遞綜合評價）權重。如表2所示，P1階次頻率（怠速振動激勵）、P2階次頻率（怠速振動激勵）及P7階次頻率（中高轉速振動激勵）對CNG公交車高壓管路的振動激勵響應最大，權重最大，其余發動機轉速下的各階次頻率對管路的振動激勵響應影響較小。

2.3 約束位置優化方案的確定

根據上述高壓管路模態振型分析結果，結合管路的實際布局結構，選擇23個潛在約束點并對其編號。然后設置這個23個約束點的邊界條件，計算各階次頻率下每個潛在約束點的振動位移量，經式（5）加權處理即可得出這23個潛在約束點的ADDOFD值。各潛在約束點的ADDOFD值分布如圖4所示。理論上因模態節點的振動為零，如果將懸掛點布置在這些節點上，則振動量最小[14]。在不影響車身及底盤結構的情況下，圖4中的波谷及附近區域可作為最終約束點的參考節點位置。

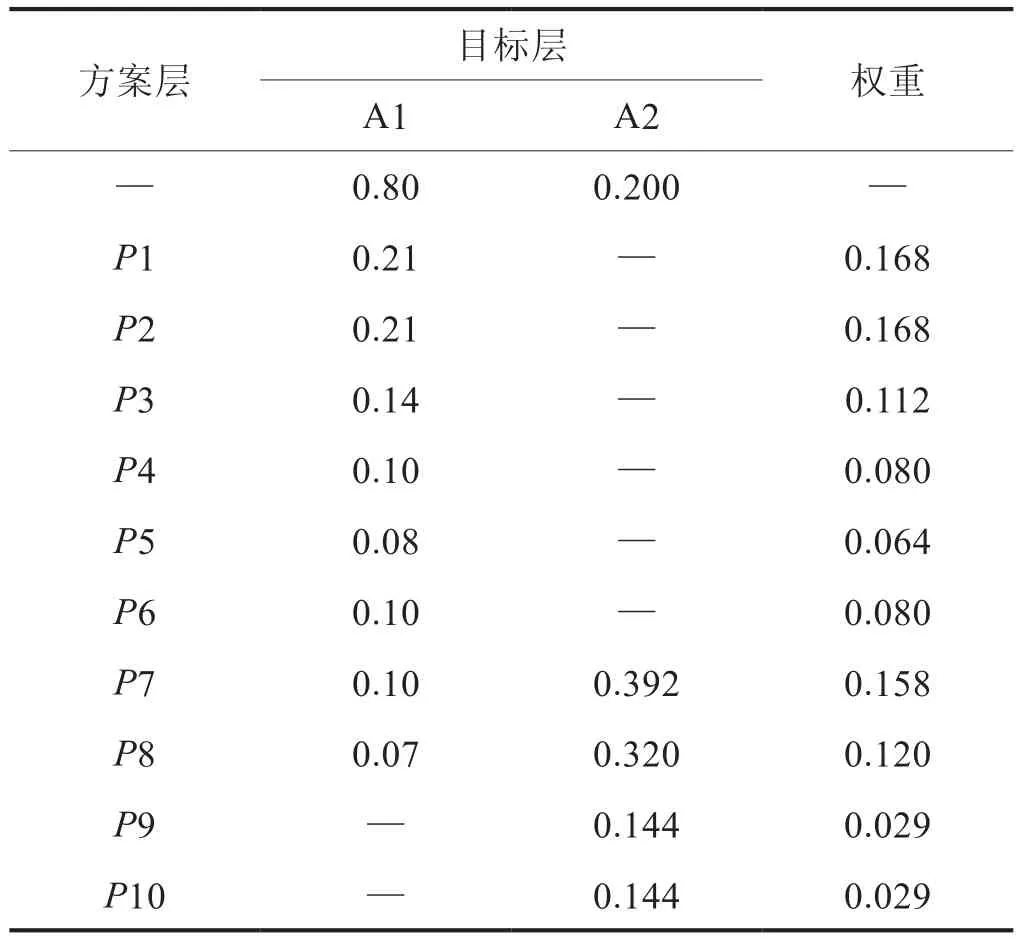
表2 方案層各階次頻率對于目標層的權重計算結果表

圖4 潛在約束點ADDOFD值圖

ADDOFD值最小，振動激勵響應程度最弱，可作為固定約束點的最佳區域[15]。圖4中，ADDOFD曲線的第3、6、14、16號潛在約束點附近存在波谷區，因此，這4個點及附近區域可作為約束點的最佳區域。結合圖4及圖5可知，實際約束點位置（如圖5所示）與圖4中的波谷位置有較大差異，即實際約束點的約束位置并不在最佳約束位置點，這說明原高壓管路實際約束點位置分布不合理，導致振動激勵響應大。特別是第1～2、4～5、7～8號實際約束點之間基本沒有固定約束。因此，結合圖4中的4個波谷區位置，需將原來的13個實際約束位點位置進行優化調整。該車高壓管路13個實際約束點位置如圖5所示，優化后的23個約束點位置如圖6所示。

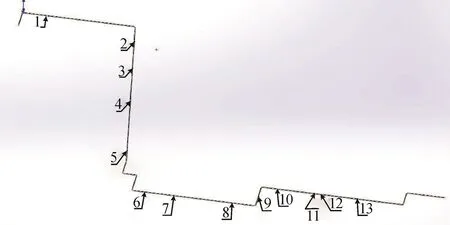
圖5 高壓管路實際約束點位置圖

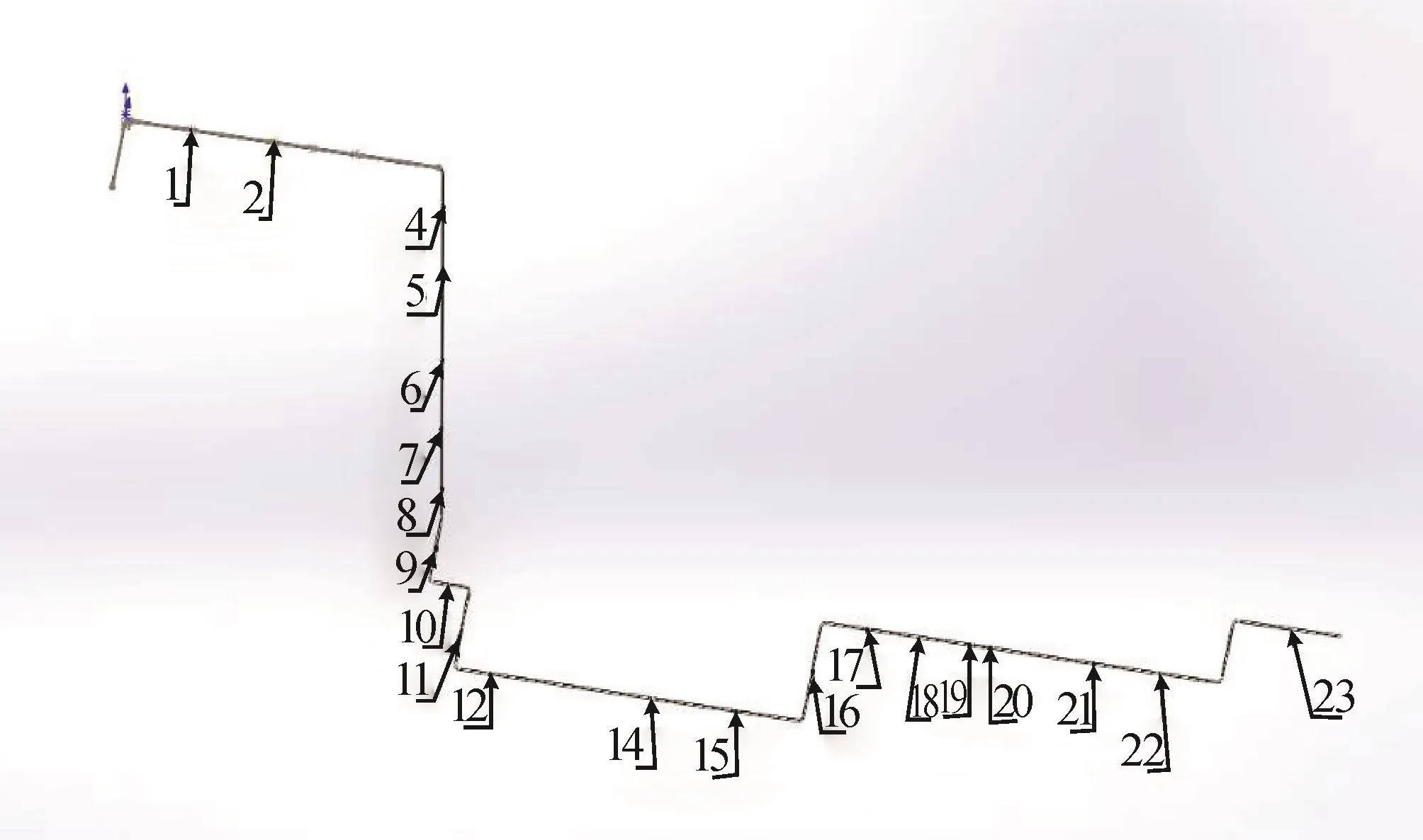
圖6 高壓管路優化后的約束點位置圖

3 優化后驗證分析

3.1 優化后模態分析

經模態計算，約束點優化后的前10階模態頻率如表3所示。

表3 約束位置優化后管路計算模態表

對比優化前后的表1和表3可知，優化后各階次頻率有較大幅度的提高，只有第1、2、3階次頻率分布在發動機轉速激勵頻率范圍內，且與發動機各工況轉速激勵都不接近，發生耦合共振的概率極低。其余的第4～10階次頻率均不在發動機轉速激勵頻率范圍內。

此外，優化后的約束點大多位于模態振型節點附近，即使與外界發生共振，也可以較大幅度降低約束和管路間的激振力傳遞，達到減振的目的。

3.2 優化后動力分析

依據該CNG公交車的發動機參數可計算出該發動機在怠速至常用轉速范圍內的激勵頻率介于26.67～73.33 Hz，查閱本文參考文獻[16]，可得激勵扭矩為100 N·m，高壓供氣管路所受主要振動激勵來自垂直方向（Z向），可在靠近發動機端的高壓管路上作用大小為100 N的Z向力，用來模擬發動機對管路的激振力作用效果。最后再進行頻率響應分析，計算在此條件下傳遞到管路固定約束上的激振力大小。優化前后4個“波谷”點的激振力分布情況如圖7、8所示。

圖7 約束位置優化前各點的激振力圖

圖8 約束位置優化后各點的激振力圖

圖7 中，當發動機激振力Z向施加高壓供氣管路100 N時，高壓管路原9號約束點的約束反力最大（約 5.87 N），對應的激振頻率為 20～ 30 Hz。

圖8中，當發動機激振力Z向施加高壓供氣管路100 N時，高壓管路的最大激振力在優化后的第16號約束點，約束反力為1.87 N。對比圖7、8可知，當激振頻率在25 Hz附近時，管路優化后的約束反力大幅度減少；當激振頻率在75 Hz附近時，管路優化后的約束反力也有一定減少；在整個頻率范圍內，優化后的管路約束點激振力均小于2 N，較原管路約束布局更加合理，達到了優化的效果。

4 結論

1）高壓管路的10個階次的固有頻率值有9個值分布在發動機各工況激勵頻率范圍內，特別是第2、3、6階次頻率與發動機常用工況轉速頻率較為接近，發生耦合共振概率較大，易造成管路疲勞損壞，影響其使用安全性和可靠性。

2）優化后的高壓供氣管路第1、2、3階次固有頻率與發動機各工況轉速激勵頻率不接近，管路發生共振的概率極小，管路其余階次的固有頻率都不在發動機各工況轉速激勵頻率范圍內，完全避免了管路共振，且優化后的約束點位置大多位于模態振型節點附近，可大幅降低約束和管路間的激振力傳遞。

3）管路約束位置優化后，約束反力在不同頻率下均有一定程度的減少，管路各約束點激振力均小于2 N，特別是在25 Hz附近，降幅最大。優化后的約束位置有利于降低管路振動，布局更加合理，達到了較好的優化效果。