基于多維相似度的整體式實體統一算法研究

范威振，陳占芳，劉燕龍

（長春理工大學 計算機科學技術學院，長春 130022）

隨著計算機技術的快速發展，信息數據逐漸呈現海量性、多源性、異構性的趨勢。如何高效的整合信息數據為數據挖掘和數據分析提供基礎服務，是當前研究的熱點［1-4］。多源異構數據在集成的過程中，通常會出現一個現實世界實體（Entity）對應多個表象（Reference）的現象，導致這種現象發生的原因可能是：拼寫錯誤、命名規則不同、名稱變體、縮寫等等。而這種現象會導致集成后的數據存在大量冗余數據、不一致數據等問題，從而降低了集成后數據的質量，進而影響了基于集成后的數據做分析挖掘的結果。分辨多個實體表象是否對應同一個實體的問題即為實體統一［5］。

實體統一的傳統做法通常是采用基于屬性特征的相關方法，這類方法旨在通過比較預設的相似度閾值與數據實體表象對應的各個屬性特征的相似度數值，從而判斷不同的表象是否對應同一實體。針對那些屬性特征完整、數據結構統一的結構化數據，這類傳統方法具有較好的度量效果。但在Web環境下，不同的數據源對相同的實體的描述不相同，普遍存在屬性特征不完整的情況，數據結構也更多的呈現半結構化或非結構化，因此只通過屬性相似度無法準確的完成實體統一。

比如從兩個系統中獲取到的兩條高校信息，如圖1所示，因為系統是在不同的年代由不同的公司開發的，其命名習慣、對實體的描述方式均不相同，屬性在很大程度上并不完整。因此，在這種情況下，判斷兩條數據是否指向同一個高校就不能只通過屬性相似度。

圖1 來自不同數據源的兩條高校信息

圖2 高校與學生數據之間的關聯

再比如說在文學領域，常常會出現“多人重名”的情況，特別是中文名字翻譯成英文時，“重名”現象就更嚴重。此時，使用“姓名”這個屬性的相似度來判斷多個表象是否對應同一個作者就不具有說服性，而且實體統一的效果也不會很好。

以上的兩個例子，都說明只使用屬性相似度已經無法準確的判斷多個實體表象是否對應同一個實體。因此，必須挖掘實體表象內部以及實體表象之間的關聯和相關信息。

例如在高校數據實體統一時，不但獲取到了高校的基本信息，而且還可以獲取到與高校相關的其他信息，如學生信息、教職工信息等。這些“上下文”信息同樣可以作為實體統一過程中的重要參考依據，如圖2所示。

再比如在社會關系網中，人們時常交往的對象總是志趣相投的；在研發領域，一個較為成熟的軟件團隊通常會研發出高質量的產品；在文學領域，興趣相投的學者可能會有所合作。這些“關系”信息對實體統一的過程也起到非常關鍵的作用。

1 實體統一算法

為了彌補傳統的實體統一算法存在的缺陷，本文采用了一種基于多維相似度的整體式實體統一算法。

本文采用一種基于圖的迭代聚類算法，來解決實體統一的問題，算法用圖來表現各個表象之間的關聯，每個實體表象都看做是一個簇（Cluster）。算法的準備階段需要完成兩項任務：一、確定一個較大的相似度閾值；二、計算各簇之間的相似度，并將結果放入優先隊列Q中。算法在循環進行實體統一時主要完成的任務是：在現有的匹配對中以相似度為依據找出最大的那組，如果該匹配對的相似度不大于預先設定的閾值，則算法結束，即實體統一工作完成，否則，將這個匹配對進行合并，形成一個新的簇，并更新與合并前的簇相關的其他簇的相似度，同時將隊列Q中的數據進行更新。算法結束時，每個簇都是一個實體，簇內的表象均對應該實體。算法的流程圖如圖3所示。

圖3 基于圖的迭代聚類算法流程圖

本文采用的算法與傳統實體統一算法的對比如表1所示。

表1 傳統實體統一算法與本文采用的算法對比表

本文采用的算法綜合使用多種相似度的度量，實體統一的過程是各匹配對彼此影響、循環往復不斷迭代的整體式的過程，因此將這種算法稱為基于多維相似度的整體式實體統一算法。基于多維相似度的整體式實體統一算法的詳細描述如表2所示。

表2 基于多維相似度的整體式實體統一算法

該算法的輸入是原始表象集S，預設較大的閾值γ，算法的輸出是統一后的簇集合C，其中每個簇都是一個實體，簇內的表象均對應該實體。

算法在第1行初始化了一個簇集合C和一個優先隊列Q，集合中存儲的是未進行實體統一的實體表象，即每個實體表象都被看做是一個簇；隊列Q用來存放匹配對。

算法的準備工作在2-4行進行，此時將集合C中的簇兩兩組合，形成一組，計算每組簇的相似度，并將該組的信息存入優先隊列中。

算法的循環匹配的工作從第5行開始，循環體里完成的工作如下：

（1）算法的第6行，在隊列Q中以相似度為依據找出最大的那組。

（2）算法的第7行，判斷獲取到的最大的這個相似度是否大于算法輸入時預設的閥值γ，如果不大于，則循環結束，即實體統一過程完成；否則，進行下面的步驟。

（3）算法的第8行，合并獲取到的該簇對。

（4）算法的第9行，更新簇集合C；算法的第10-14行，更新與相似度最大的簇對有關的簇；算法的15-19行，更新相似度最大的簇對的“鄰居”簇；

算法在第21行返回實體統一后的簇集合C，集合中的每個簇都是一個實體，簇內的表象均對應該實體。

2 相似度度量方法

由上文的介紹可知，只使用屬性相似度存在許多的不足，本節將詳細的介紹本方法中綜合使用的三種相似度度量方法。

2.1 屬性相似度度量

基于屬性的相似度作為實體統一過程中較為常用的參考依據，有關學者已做出了較深入的探索，已經研究出了許多精確而有效的相似度度量方式，如基于文本字符的實體統一方式、基于標記的實體統一方式、基于發音與語法規則的統一方式等等［6-8］。

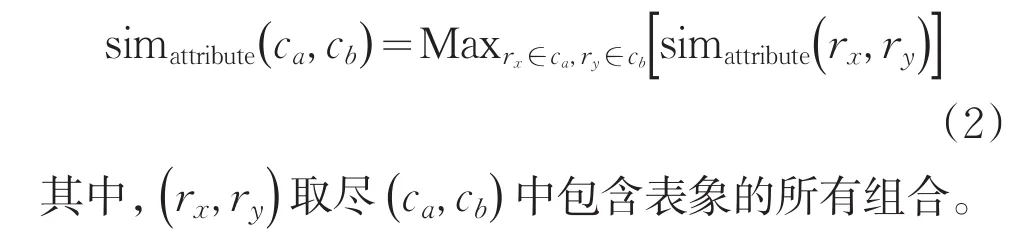
2.2 上下文相似度度量

為了更加全面的衡量兩個簇的相似程度，在使用屬性相似度的基礎上，還要考慮簇中表象對的上下文相似度。

在不同的環境下，實體表象的上下文有很大差異。如在文獻領域，針對作者這一表象，作者的合作者是其重要的上下文，隨著表象對間的合作者相同的個數增加，該表象對對應一個實體的概率也在不斷的增加。

由此發現：在度量表象對上下文的相似度時，只需利用表象對的上下文進行相應的屬性相似度的運算即可，不需要對兩個實體表象的上下文進行限制，即兩個實體表象的上下文屬性不需要“一一對應”。

2.3 關系相似度度量

在現實應用的過程中，實體表象之間的關聯很復雜。比如在社會關系網中，人們時常交往的對象總是志趣相投的；在研發領域，一個較為成熟的軟件團隊通常會研發出高質量的產品；在文學領域，興趣相投的學者可能會有所合作。

實體表象之間的這種共現關系，暗含了“團體”的存在，在很大程度上可以輔助判斷實體表象的同指關系，即有利于分辨多個表象是不是對應同一個實體。因此，具有關聯性的實體表象之間連接的緊密程度，將是判斷多個實體表象是否指向同一實體的重要信息，本文中表象對間的關系相似度可通過計算具有關聯性的實體表象之間連接的緊密程度來衡量。

為了挖掘實體表象之間隱藏的這種“團體”特征，可以通過引入“相似團”（Quasi-Clique）這種數據結構來輔助操作。下面給出相關的定義。

對于無向圖G(V,E)而言，V(G)指G中所有頂點的集合，E(G)指G中所有邊的集合，size(V(G))指G中頂點的個數，size(E(Vi))指經過Vi的所有邊的個數。

如果圖G中任一頂點起碼有γ(size(V(G))-1)個邊，即

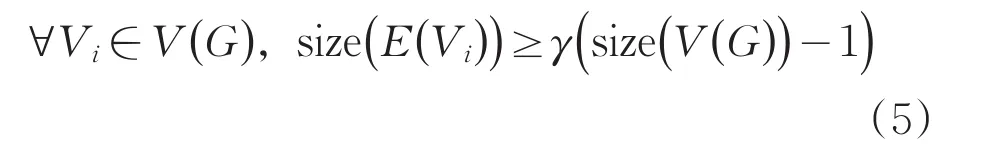
則稱圖G為γ-相似完全圖，其中0≤γ≤1。

例如圖4（a）為1-相似完全圖，即完全圖，圖4（b）為0.7-相似完全圖。

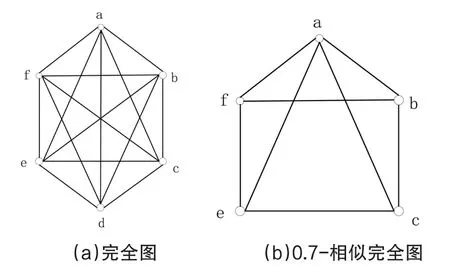
圖4 完全圖和相似完全圖

對于G的子圖S而言，如果子圖S符合γ-相似完全圖的定義，則稱S為G的γ-相似團圖（γ-Quasi-Clique）。其中，V(S)?V(G)、E(S)?E(G)。很顯然1-相似團圖是完全圖，即為團。

例如對于圖4（a）而言，其本身為1-相似團圖，圖4（b）為其0.7-相似團圖。

根據上面的定義，不難發現γ-相似團具有一個非常好的特質：圖的連接緊密程度與γ值的大小成正比。即當γ的值越大時，圖中邊也就越多，圖中頂點間連接緊密的程度越高；反之，當γ的值越小時，圖中邊的個數就越少，圖中頂點間的連接緊密程度越低。本文通過對“相似團”的挖掘，來研究實體表象之間隱藏的“團體”特征；用γ的值來度量“團體”中實體表象之間的連接緊密程度，即實體表象之間的關系相似度。

基于上文的分析，(ca,cb)間關系相似度的度量過程是：第一步，用(ca,cb)的鄰接關系抽象出實體表象的關系圖G；第二步，在已有的關系圖中用相似團挖掘算法找出γ較大的相似團圖S；此時(ca,cb)間的關系相似度simrelationship(ca,cb)定義如下：

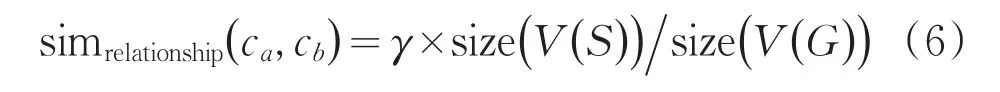
其中，γ代表了相似團圖中頂點的連接緊密程度，size(V(S))表示相似團圖S中頂點的個數，size(V(G))表示類(ca,cb)間公共頂點的個數。

3 實驗及結果分析

3.1 實驗環境與數據集

本文實驗環境如表3所示。

表3 實驗環境表

本文所采用的算法適用于多種復雜的場景，此處選擇對文獻信息進行實驗來研究算法的性能。數據集使用Patrick Reuther整理的DBLP數據集，該數據集是已經標注了統一后真實情況的部分DBLP網站上的文獻信息。可以利用這些已經處理后的數據進行實驗來研究本文采用算法的準確性和效率。

DBLP數據集是以XML的形式存在的，其信息描述格式如下：

實驗使用了三個DBLP的數據集，其基本情況如表4所示。

表4 實驗使用數據集的描述表

3.2 評價標準

通過上文的描述可知，本文所用算法的輸出結果是實體統一后的簇集合C，其中每個簇表示一個實體，簇中的元素為指向該實體的表象。為了更好的評價算法的準確性和性能，可以將算法的輸出結果分為Set1,Set2,Set3,Set4四個集合，各集合意義如表5所示。

表5 算法輸出結果分類意義表

用Size(Seti)表示第i個集合內元素的個數，則可以定義查準率（Precision）、查全率（Recall）和F1：

其中，Precision表示在實驗的所有結果中，實體統一正確的簇所占的比例，該比例反應了實體統一的正確與否，即為查準率；Recall表示實驗的結果中，實體統一正確的簇在真實的簇中占到的比例，該比例反應了實體統一的覆蓋程度，即為查全率；F1作為實體統一的綜合評價指標。

3.3 實驗結果分析

為了清晰的比較算法在三種相似度上的差異，針對每個數據集都進行了三組實驗：只使用屬性相似度(Attr)、使用屬性相似度和上下文相似度（Attr+Con）、三種相似度都使用（Attr+Con+Rela）。

將實驗的結果，按照上文的評價標準可求得每組實驗的Precision、Recall和F1，匯總后如圖5所示。

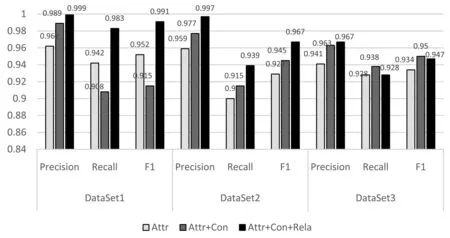
圖5 實驗的結果對比圖

由圖5可知：

（1）對三個數據集來說，Attr+Con+Rela組實體統一實驗效果最好，整體性能最高。

（2）對于DataSet1上的三組實驗結果，就準確性進行比較：Attr＜Attr+Con，Attr+Con＜Attr+Con+Rela；就 Recall和F1進行比較是 Attr＞Attr+Con，Attr＜Attr+Con+Rela。

對于（1），證明綜合使用三種相似度，實驗結果的整體性能得到了提升；對于（2），說明相比于只使用屬性相似度而言，在綜合使用屬性相似度和上下文相似度時，算法的準確性雖然得以提升，但如果數據之間存在一定的“自反性”，那么在一定程度上會干擾算法的判斷，從而影響算法的性能。

因此，可以得出結論：相比于只使用單一的屬性相似度，使用多種相似度可有效的提供實體統一的效果。

4 總結

針對傳統實體統一算法存在的弊端，本文采用了一種基于多維相似度的整體式實體統一算法。采用了一種基于圖的迭代聚類的整體式實體統一算法，綜合使用了屬性、“上下文”、“關系”等信息來進行了相似度的度量，實體統一算法是各匹配對彼此影響、循環往復不斷迭代的整體式的過程。最后在多個數據集上進行多組實驗進行對比，測試算法在實體統一方面的性能。